Сравнение эффективности алгоритмов на Python

1. Сравнение эффективности алгоритмов на Python

С РА В Н Е Н И Е
ЭФФЕКТИВНОСТИ
АЛГОРИТМОВ НА
PYTHON
Работу выполнил:
Ученик 9М класса
Зорков Михаил

2. Введение

ВВЕДЕНИЕ
В современном мире обрабатываемых данных ежедневно измеряется петабайтами. Изза этого эффективность алгоритмов становится не просто теоретическим понятием, а
практической необходимостью. От скорости сортировки данных зависит работа
поисковых систем, банковских транзакций, медицинских исследований и даже игровых
Сортировка является одной из фундаментальных операций в информатике. Хотя для
обработки больших массивов данных сегодня используются сложные алгоритмы с
временной сложностью O (n log(n)), понимание более простых методов остается важным
по нескольким причинам. Во-первых, они образуют базу для изучения алгоритмов. Вовторых, в некоторых специфических случаях простые алгоритмы могут оказаться
эффективнее своих сложных аналогов. В-третьих, они часто используются как
составные части более сложных алгоритмов.
1 2 . 0 2 . 2 0 2 6
приложений на смартфонах.
2

3. Цель работы

Ц Е Л Ь РА Б О Т Ы
Сравнить эффективность двух классических алгоритмов сортировки — пузырьковой
и
выбором
—
на
различных
типах
данных
с
использованием
языка
программирования Python
3
1 2 . 0 2 . 2 0 2 6

4. задачи

З А Д АЧ И
⦁ Изучить основы и принципы работы алгоритмов пузырьковой сортировки и
сортировки выбором
⦁ Реализовать оба алгоритма на языке Python с добавлением инструментария для
измерения производительности (matplotlib)
⦁ Провести серию экспериментов по измерению времени выполнения и подсчету
операций сравнения и перестановки
⦁ Проанализировать полученные результаты и сформулировать практические
рекомендации по выбору алгоритма в зависимости от условий задачи
1 2 . 0 2 . 2 0 2 6
⦁ Разработать методику экспериментального исследования, включающую различные
типы и размеры тестовых данных
4

5. Пузырьковая сортировка

П У З Ы Р Ь К О ВА Я СО РТ И РО В К А
Впервые описана в 1956 году, однако
есть свидетельства, что этот метод
использовался и ранее. Название
алгоритма отражает его суть: элементы с
"всплывают" к концу массива, подобно
пузырькам воздуха в воде. Несмотря на
свою неэффективность для больших
массивов, алгоритм остается популярным
в образовательных целях благодаря
простоте реализации.
1 2 . 0 2 . 2 0 2 6
большими значениями постепенно
5

6. Сортировка выбором

СОРТИРОВКА ВЫБОРОМ
6
1 2 . 0 2 . 2 0 2 6
Первые упоминания алгоритма относятся к
середине 1950-х годов, хотя его логика
применялась программистами еще до
появления формальных описаний.
Название метода прямо указывает на
принцип его работы: на каждом шаге из
неотсортированной части массива
выбирается минимальный элемент, который
переносится на свою итоговую позицию.
Несмотря на низкую производительность на
больших объемах данных, алгоритм
ценится в обучении за наглядность и
минимальное количество операций
перезаписи в памяти

7. Сравнение вычислительной сложности алгоритмов

С РА В Н Е Н И Е В Ы Ч И С Л И Т Е Л Ь Н О Й
СЛОЖНОСТИ АЛГОРИТМОВ
⦁ Худший случай: O(n²) — с
меньшей константой, чем у
пузырьковой сортировки
Средний случай: O(n²) — для
случайных данных
⦁ Средний случай: O(n²) —
количество сравнений постоянно для
любого порядка элементов
Лучший случай: O(n) — когда
массив уже отсортирован (при
оптимизированной реализации с
флагом обмена)
⦁ Лучший случай: O(n²) — алгоритм
всегда производит полное
количество сравнений
Память: O(1) — алгоритм
сортирует на месте, не требуя
дополнительной памяти.
⦁ Память: O(1) — алгоритм так же
сортирует на месте
7
1 2 . 0 2 . 2 0 2 6
Худший случай: O(n²) — когда
массив отсортирован в обратном
порядке

8. Практическая часть: параметры и план экспериментов

П РА К Т И Ч Е С К А Я Ч А С Т Ь : П А РА М Е Т Р Ы
И ПЛАН ЭКСПЕРИМЕНТОВ
Типы тестовых данных:
Размеры массивов: 2000, 4000,
⦁ Случайные массивы (random)
— элементы распределены
случайном образом в диапазоне от
0 до 10000
6000, 8000, 10000, 12000
⦁ Упорядоченные массивы
(sorted) — элементы расположены
по возрастанию
комбинации параметров
⦁ Обратно упорядоченные
массивы (reversed) — элементы
расположены по убыванию
минимизации влияния случайных
элементов
8
эксперимент для заданной
повторялся 3-5 раз с последующим
усреднением результатов для
факторов
1 2 . 0 2 . 2 0 2 6
Количество повторений: каждый

9. Практическая часть: Эксперимент №1, суть и цель

П РА К Т И Ч Е С К А Я Ч А С Т Ь :
ЭКСПЕРИМЕНТ №1, СУТЬ И ЦЕЛЬ
Суть эксперимента: сравнить эффективность алгоритмов на типичных данных.
Цель: определить, какой из алгоритмов является более эффективным при
обработке случайных, неупорядоченных данных.
9
1 2 . 0 2 . 2 0 2 6

10. Практическая часть: Эксперимент №1, построение графиков

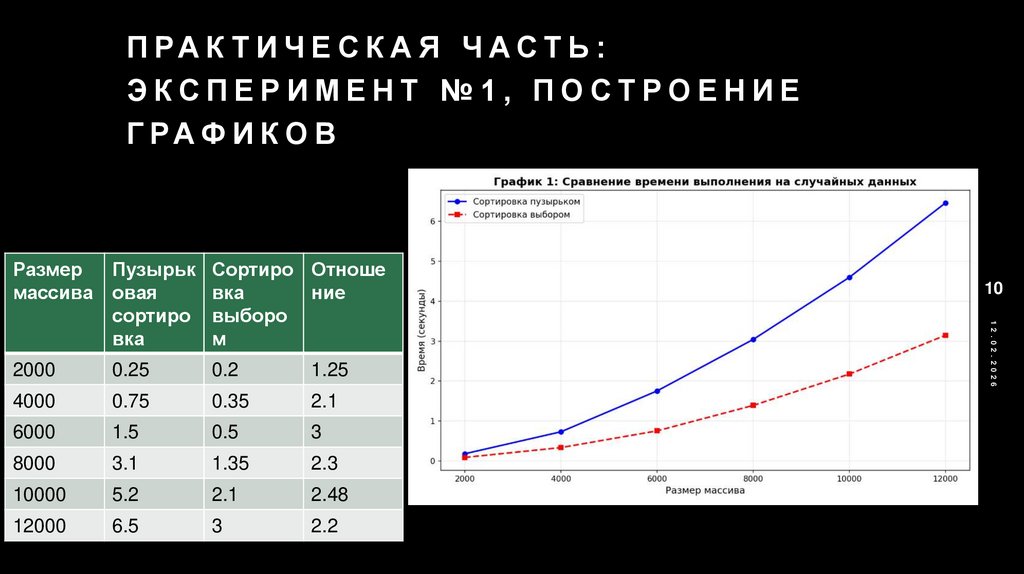
П РА К Т И Ч Е С К А Я Ч А С Т Ь :
ЭКСПЕРИМЕНТ №1, ПОСТРОЕНИЕ
Г РА Ф И К О В
Пузырьк
овая
сортиро
вка
Сортиро Отноше
вка
ние
выборо
м
2000
0.25
0.2
1.25
4000
0.75
0.35
2.1
6000
1.5
0.5
3
8000
3.1
1.35
2.3
10000
5.2
2.1
2.48
12000
6.5
3
2.2
10
1 2 . 0 2 . 2 0 2 6
Размер
массива

11. Практическая часть: Эксперимент №1, анализ результатов

П РА К Т И Ч Е С К А Я Ч А С Т Ь :
ЭКСПЕРИМЕНТ №1, АНАЛИЗ
Р Е З У Л ЬТ А Т О В
⦁
Сортировка выбором демонстрирует стабильное преимущество примерно в 2,2
раза на всех размерах массивов
⦁
Время выполнения обоих алгоритмов растет квадратично, что подтверждается
примерно в 9 раз
⦁
Отношение времени выполнения остается практически постоянным, что
свидетельствует о схожей асимптотической сложности, но разной константе в
формуле O(n²)
1 2 . 0 2 . 2 0 2 6
визуально: при увеличении размера в 3 раза (с 4000 до 12000) время возрастает
11

12. Практическая часть: Эксперимент №2, суть и цель

П РА К Т И Ч Е С К А Я Ч А С Т Ь :
ЭКСПЕРИМЕНТ №2, СУТЬ И ЦЕЛЬ
Суть эксперимента: исследование адаптивных свойств алгоритмов - их зависимость
от входных данных.
Цель: определить, насколько производительность каждого алгоритма зависит от
алгоритма.
1 2 . 0 2 . 2 0 2 6
исходного состояния данных, выявить лучшие и худшие случаи для каждого
12

13. Практическая часть: Эксперимент №2, построение графиков

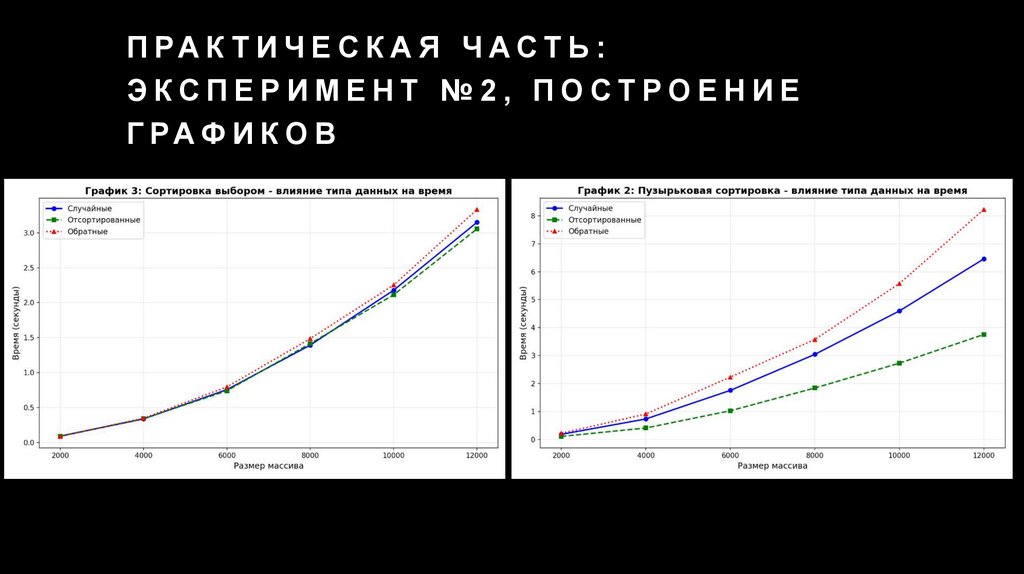
П РА К Т И Ч Е С К А Я Ч А С Т Ь :
ЭКСПЕРИМЕНТ №2, ПОСТРОЕНИЕ
Г РА Ф И К О В
13
1 2 . 0 2 . 2 0 2 6

14. Практическая часть: Эксперимент №2, анализ результатов

П РА К Т И Ч Е С К А Я Ч А С Т Ь :
ЭКСПЕРИМЕНТ №2, АНАЛИЗ
Р Е З У Л ЬТ А Т О В
⦁
Пузырьковая сортировка является адаптивным алгоритмом — ее
производительность сильно зависит от исходной упорядоченности данных
⦁
Сортировка выбором — неадаптивный алгоритм — ее производительность
⦁
На обратно отсортированных массивах пузырьковая сортировка показывает
наихудшие результаты, в то время как сортировка выбором сохраняет
стабильную производительность
1 2 . 0 2 . 2 0 2 6
практически не зависит от входных данных
14

15. Практическая часть: Эксперимент №3, суть и цель

П РА К Т И Ч Е С К А Я Ч А С Т Ь :
ЭКСПЕРИМЕНТ №3, СУТЬ И ЦЕЛЬ
Суть эксперимента: подсчитать количество элементарных операций перестановки
элементов в массиве при сортировке. Это отделит алгоритмическую эффективность
от аппаратной производительности
15
⦁
Объяснить причины временных различий
⦁
Сравнить алгоритмы на теоретическом уровне
⦁
Выявить ключевое отличие между алгоритмами
1 2 . 0 2 . 2 0 2 6
Цели:

16. Практическая часть: Эксперимент №3, построение графиков

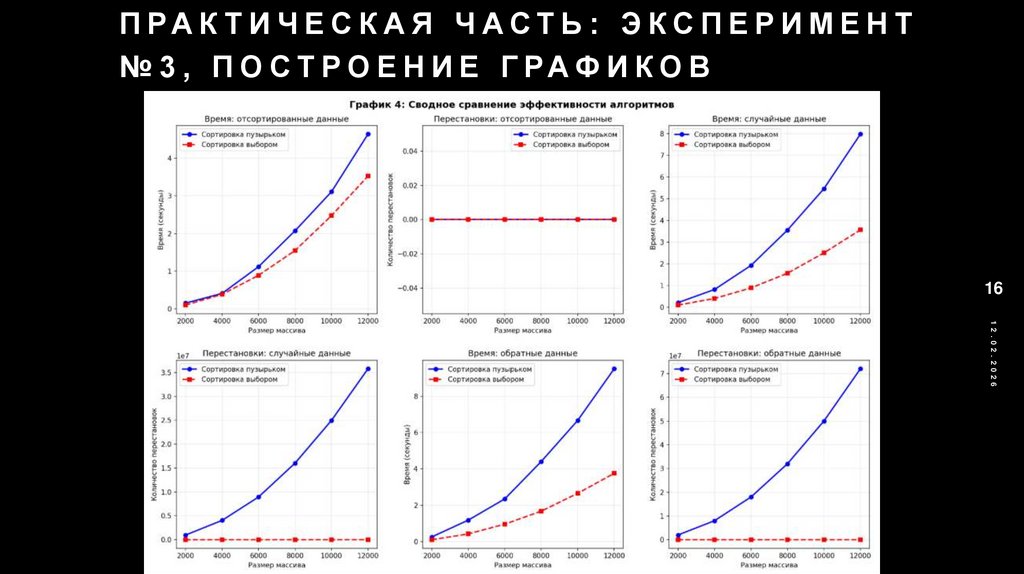
П РА К Т И Ч Е С К А Я Ч А С Т Ь : Э К С П Е Р И М Е Н Т
№ 3 , П О С Т Р О Е Н И Е Г РА Ф И К О В
16
1 2 . 0 2 . 2 0 2 6

17. Практическая часть: Эксперимент №3, анализ результатов

П РА К Т И Ч Е С К А Я Ч А С Т Ь :
ЭКСПЕРИМЕНТ №3, АНАЛИЗ
Р Е З У Л ЬТ А Т О В
⦁
Количество сравнений для обоих алгоритмов равно n²/2
⦁
Количество перестановок для пузырьковой сортировки равняется n²/4, а у
сортировки выбором n-1
Разница в количестве перестановок объясняет, почему сортировка выбором
лучше, чем пузырьковая
1 2 . 0 2 . 2 0 2 6
⦁
17

18. Сводный анализ практической части

С В О Д Н Ы Й А Н А Л И З П РА К Т И Ч Е С К О Й
ЧАСТИ
На основе всех проведенных экспериментов можно составить комплексную
характеристику каждого алгоритма:
Пузырьковая сортировка:
Сортировка выбором:
⦁ Слабые стороны: крайне низкая
производительность на больших и/или
обратно отсортированных массивах;
большое количество операций обмена
реализации
⦁ Слабые стороны: квадратичная
сложность во всех случаях; отсутствие
адаптивности; неустойчивость в базовой
реализации
1 2 . 0 2 . 2 0 2 6
⦁ Сильные стороны: исключительная
⦁ Сильные стороны: стабильная
эффективность на уже отсортированных или производительность независимо от
почти отсортированных данных; простота
входных данных; минимальное
реализации; устойчивость
количество операций обмена; простота
18

19. Вывод из исследования:

В Ы ВОД И З И С СЛ Е Д О ВА Н И Я :
Проведенное исследование доказало, что сортировка выбором является более
эффективным алгоритмом сортировки, чем пузырьковая сортировка, демонстрируя
преимущество в среднем в 2 раза, благодаря меньшему количеству перестановок.
19
1 2 . 0 2 . 2 0 2 6

20. Список литературы

С П И С О К Л И Т Е РАТ У Р Ы
https://docs.python.org/3/
https://matplotlib.org/3.5.3/api/_as_gen/matplotlib.pyplot.html
https://cs.mipt.ru/python/lessons/lab1.html
20
1 2 . 0 2 . 2 0 2 6