Geometricheskie_fraktaly

1.

2.

fractus (лат) - состоящий из фрагментов, расколотый,
нерегулярный.
Термины “fraction”, “fractional” – дробь, дробный.
Термин “фрактал” ввел Бенуа Мандельброт в 1975г. для
обозначения
нерегулярных,
но
самоподобных
структур.
Фракталом называется структура, состоящая из частей,
которые в каком-то смысле подобны целому
(Б.Мандельброт).

3.

Свойства фракталов
Самоподобие – одно из основных
свойств фракталов. В самом простом
случае небольшая часть фрактала
содержит
информацию
о
всем
фрактале. Второе свойство – объект с
дробной размерностью.

4.

• Разделим отрезок прямой на N равных частей. Тогда
каждую часть можно считать копией всего отрезка,
уменьшенного в 1/r раз. Очевидно, N и r связаны
отношением Nr = 1.
• Если квадрат разбить на N равных квадратов (с
площадью, в 1/r^2 раз меньше площади исходного),
то соотношение запишется как Nr^2 = 1.
Соответственно, общая формула:
• Nr^d = 1.
(1)
• Множества, построенные выше, обладают целой
размерностью. Возможно ли такое построение, при
котором показатель d в равенстве (1) НЕ является
целым? Такое множество называется самоподобным
фракталом. Величину d называют фрактальной
(дробной) размерностью или размерностью
подобия. Явное выражение для d через N и r
находится логарифмированием обеих частей (1)
• d = (Log N) / (Log 1/r)

5.

«Почему геометрию часто называют холодной
и сухой? Одна из причин заключается в ее
неспособности описать форму облака, горы,
дерева или берега моря. Облака - это не
сферы, горы - не конусы, линии берега - это не
окружности, и кора не является гладкой, и
молния не распространяется по прямой.
Природа демонстрирует нам не просто более
высокую степень, а совсем другой уровень
сложности».
Б. Мандельброт

6.

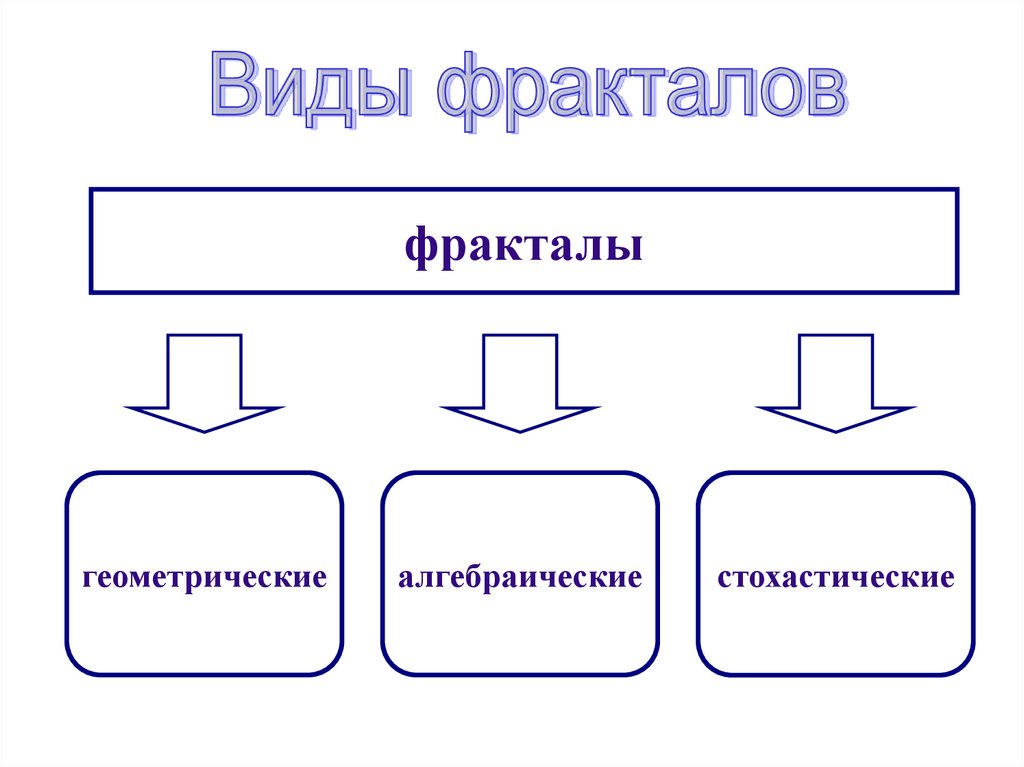
фракталы
геометрические
алгебраические
стохастические

7.

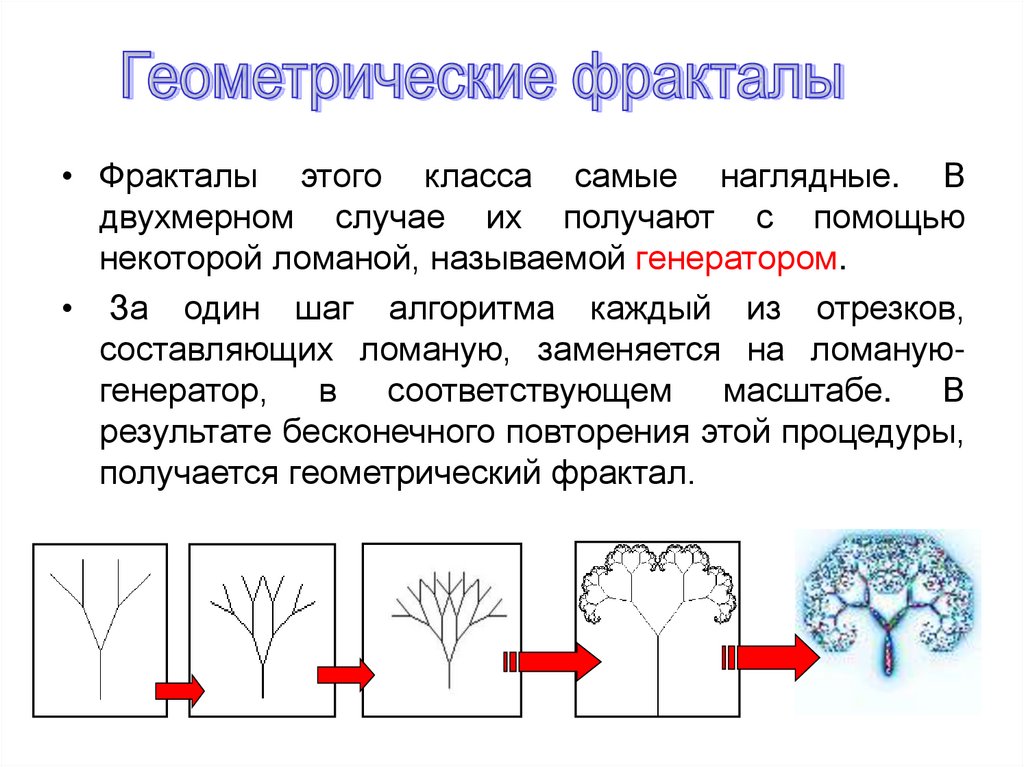
• Фракталы этого класса самые наглядные. В
двухмерном случае их получают с помощью
некоторой ломаной, называемой генератором.
• За один шаг алгоритма каждый из отрезков,
составляющих ломаную, заменяется на ломануюгенератор, в соответствующем масштабе. В
результате бесконечного повторения этой процедуры,
получается геометрический фрактал.

8.

9.

Кривая Коха
• Эта кривая описана в 1904 г. шведским
математиком Хельге фон Кохом (18701924), по результатам изучения работ
Карла Вейерштрасса и Георга Кантора.
• Кривая Коха примечательна тем, что
она всюду непрерывна, но нигде
недифференцируема (т.е. не имеет
касательной).

10.

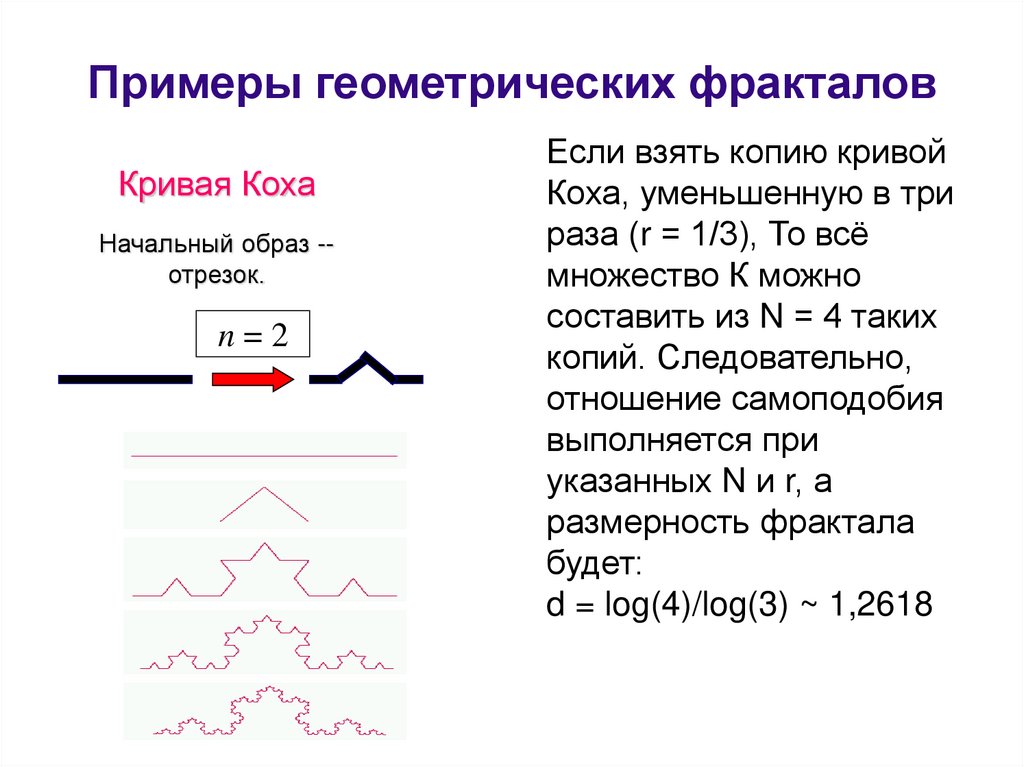
Примеры геометрических фракталов
Кривая Коха
Начальный образ -отрезок.
n=2
Если взять копию кривой
Коха, уменьшенную в три
раза (r = 1/3), То всё
множество К можно
составить из N = 4 таких
копий. Следовательно,
отношение самоподобия
выполняется при
указанных N и r, а
размерность фрактала
будет:
d = log(4)/log(3) ~ 1,2618

11.

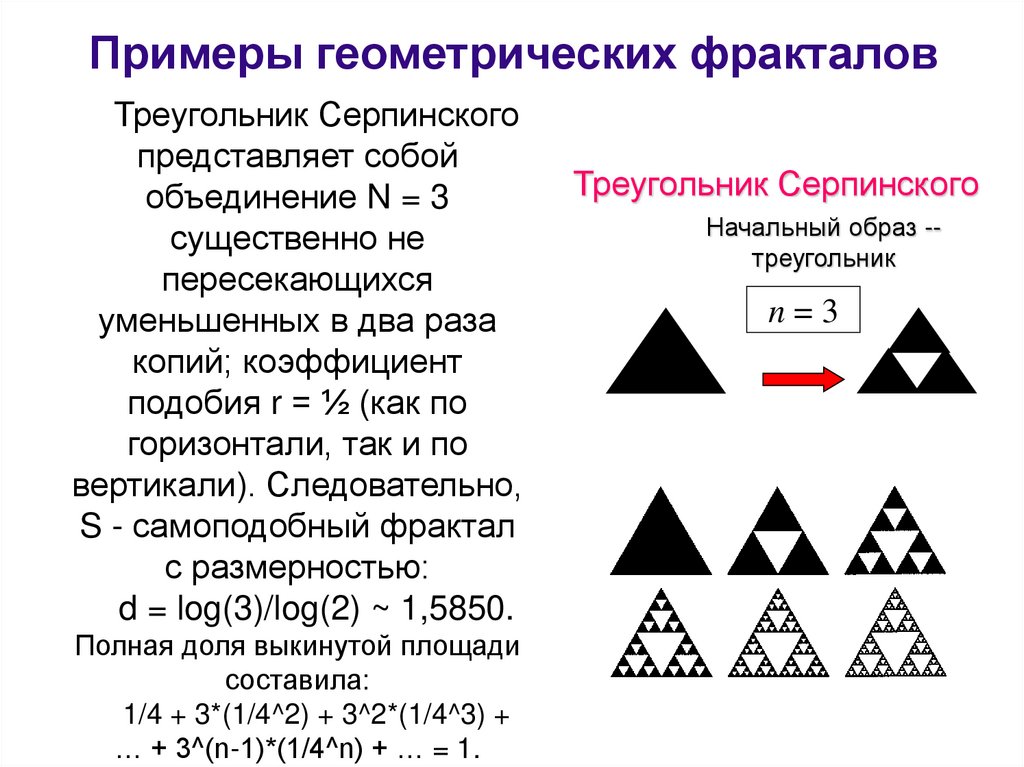
Примеры геометрических фракталов
Треугольник Серпинского
представляет собой
объединение N = 3
существенно не
пересекающихся
уменьшенных в два раза
копий; коэффициент
подобия r = ½ (как по
горизонтали, так и по
вертикали). Следовательно,
S - самоподобный фрактал
с размерностью:
d = log(3)/log(2) ~ 1,5850.
Полная доля выкинутой площади
составила:
1/4 + 3*(1/4^2) + 3^2*(1/4^3) +
… + 3^(n-1)*(1/4^n) + … = 1.
Треугольник Серпинского
Начальный образ -треугольник
n=3

12.

13.

Геометрические фракталы обладают
жесткой
самоподобностью
не
изменяющейся
при
изменении
масштаба.
Примерами
таких
фракталов
являются
треугольник
Серпинского, снежинка Коха, ковер
Серпинского, кривая Леви.