алгебраические Фракталы

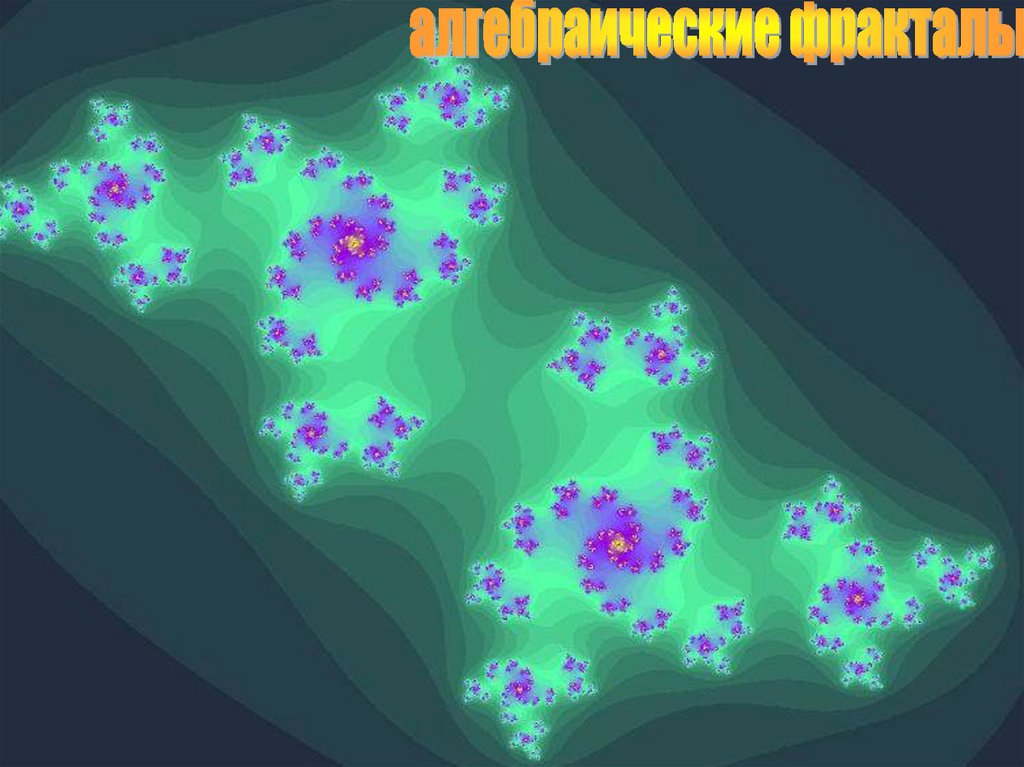
1. Алгебраические фракталы

Итерационный метод получения алгебраических
фракталов: многократный расчет функции zn+1 = f(zn), где
z - комплексное число, а f - некая функция.
Для
каждой
точки
комплексной
плоскости
итерационный расчет значения продолжается до
выполнения определенного условия, когда это условие
выполнится - на экран выводится точка.

2. Мно́жество Мандельбро́та — это фрактал, определённый как множество комплексных точек с, для которых последовательность z0 = 0;

zn+1 = zn2 + c
не уходит в бесконечность.
Одним
из
самых
распространённых
способов
раскрашивания точек будет сравнение | z | с заранее
выбранным числом, которое считается «бесконечным»,
т. е. цвет точки равен номеру итерации, на которой | z |
достиг «бесконечности», или чёрному в противном
случае. Для приведенной формулы это 2.

3. Алгоритм построения

• Выбираем часть комплексной плоскости
• Каждая ее точка соответствует значению С в
итерационном процессе
• Для точки на мониторе определяем ее координаты в
компл. плоскости, запускаем итерационный процесс
на выбранное нами число итераций
• Если за это время точка не ушла на “бесконечность”,
закрашиваем ее “черным”
• В противном случае цвет зависит от числа итераций,
за которое точка уйдет на бесконечность – плавно
или выбирается цвет из фиксированной палитры

4.

5.

Меняя функцию и условие выхода из цикла можно
получать другие фракталы.
Множество Жюлиа – константа c фиксирована, а меняются
начальные точки.

6.

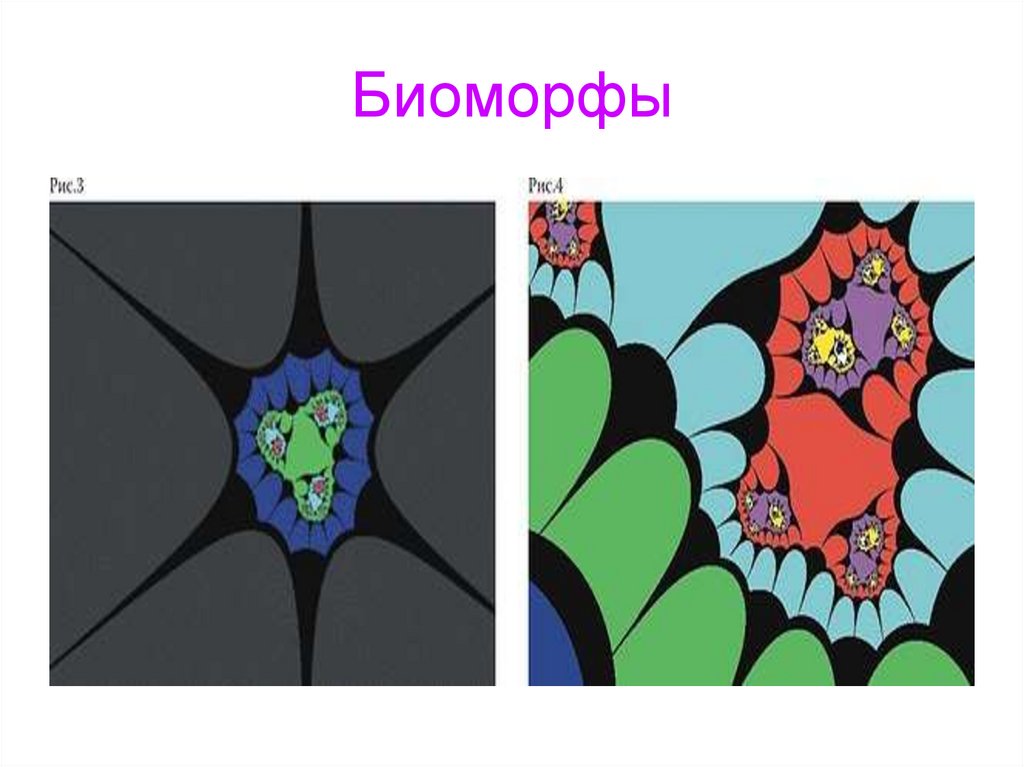
7. Биоморфы

8.

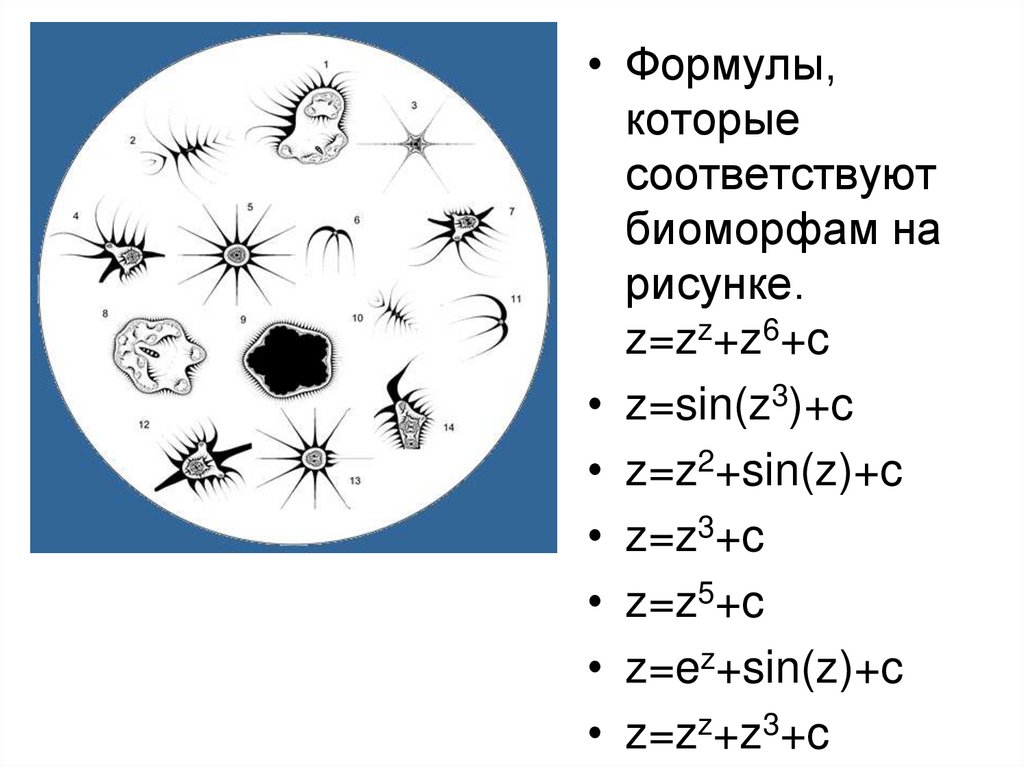
• Формулы,
которые
соответствуют
биоморфам на
рисунке.
z=zz+z6+c
• z=sin(z3)+c
• z=z2+sin(z)+c
• z=z3+c
• z=z5+c
• z=ez+sin(z)+c
• z=zz+z3+c

9.

• В итерационном процессе случайным образом
меняются какие-либо параметры.
• Получаются объекты очень похожие на
природные - несимметричные деревья,
изрезанные береговые линии и т.д.
• С помощью компьютера такие процессы
строить достаточно просто, т.к. он позволяет
генерировать последовательности случайных
чисел.

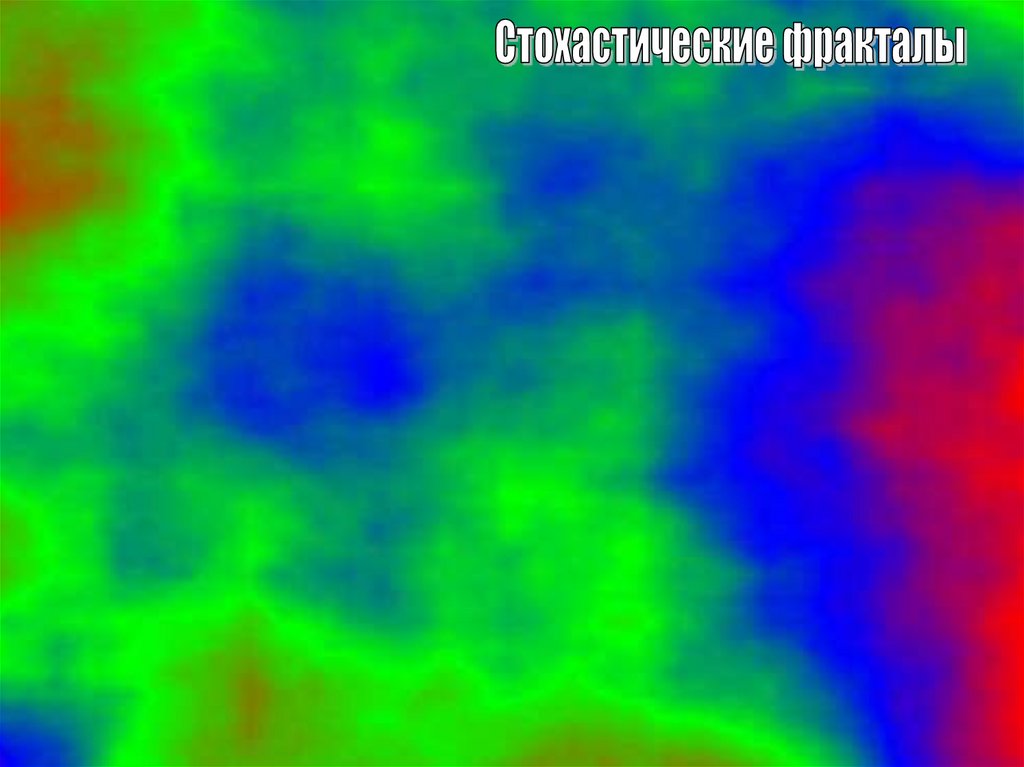
10.

Двумерные
стохастические
фракталы
используются при моделировании рельефа
местности и поверхности моря, процесса
электролиза, техники броуновского движения,
используется для создания ландшафтных
дизайнов.

11. Стохастический фрактал “плазма”

Стохастический фрактал “плазма”
Для её построения возьмём
прямоугольник и для каждого
его угла определим цвет. Далее
находим центральные точки
прямоугольника и его сторон, и
раскрашиваем их в цвет,
равный среднему
арифметическому цветов по
углам прямоугольника плюс
некоторое случайное число,
пропорциональное размеру
разбиваемого прямоугольника.
Прямоугольник разбиваем на 4
равных, к каждому из которых
применяется та же процедура.
Далее процесс повторяется.
Чем больше случайное число —
тем более «рваным» будет
рисунок.
•Если мы теперь скажем, что цвет точки — это высота над уровнем моря,
то вместо плазмы получим горный массив. Именно на этом принципе
моделируются горы в большинстве программ. С помощью алгоритма,
похожего на плазму, строится карта высот, к ней применяются различные
фильтры, накладывается текстура и т. д.

12. Фракталы в информатике

• Описание сложных объектов, рекурсивных
(фрактальных) по своей природе. Фактически
найден способ легкого представления
сложных неевклидовых объектов, образы
которых весьма похожи на природные.
• Нахождение фрактального описания объектов
при сжатии информации.
• Фрактальные генераторы часто используются
для генерации ландшафта в играх (с помощью
нескольких коэффициентов задаются линии и
поверхности очень сложной формы)!

13. Фракталы в других областях

• Анализ и классификация сигналов сложной
формы, возникающих в разных областях.
• Рынок ценных бумаг имеет фрактальную
структуру.
• Физика твердого тела, динамика активных
сред.
• В медицине (наши легкие имеют фрактальную
структуру).
• Современные
антенны
–
фракталы
(уменьшение веса и размера).

14.

Горы, облака, границы берегов - все это выходит за
рамки привычной евклидовой геометрии.
Мы не можем описать структуру кораллов, крону
деревьев, листья с помощью прямых, кружков и
треугольников. И здесь нам приходят на помощь фракталы.