f3392d764b664de2b78476205b5a15e7

1.

2.

Высказывание
— это предложение, в отношении которого можно
сказать, истинно оно или ложно
Примеры истинных высказываний
Примеры ложных высказываний
"Москва — столица России"
"2 + 2 = 4"
• "2 + 2 = 5" (Л)
• "Волга впадает в Чёрное море" (Л)
Не являются высказываниями:
• Вопросы: "Который час?"
• Побуждения: "Откройте учебник!"
• Предложения с переменными: "x > 5"

3.

Логическая переменная
— переменная, принимающая только два
значения: "истина" или "ложь"
Обозначения:
Истина
Ложь
И
Л
true
false
1
0
да
нет

4.

Краткая биография:
• Английский математик
• Создал алгебру логики в 1854 году
• Основные операции: AND, OR, NOT
• Применение в компьютерных науках (Клод
Шеннон, 1938)
Джордж Буль (1815–1864)

5.

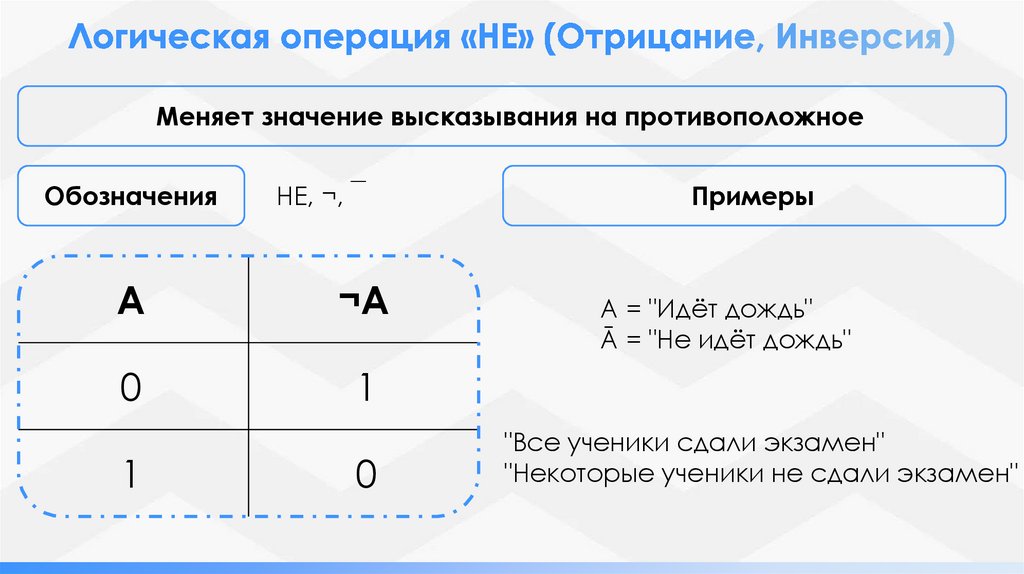
Меняет значение высказывания на противоположное
Обозначения
НЕ, ¬, ‾
A
¬A
0
1
1
0
Примеры
A = "Идёт дождь"
Ā = "Не идёт дождь"
"Все ученики сдали экзамен"
"Некоторые ученики не сдали экзамен"

6.

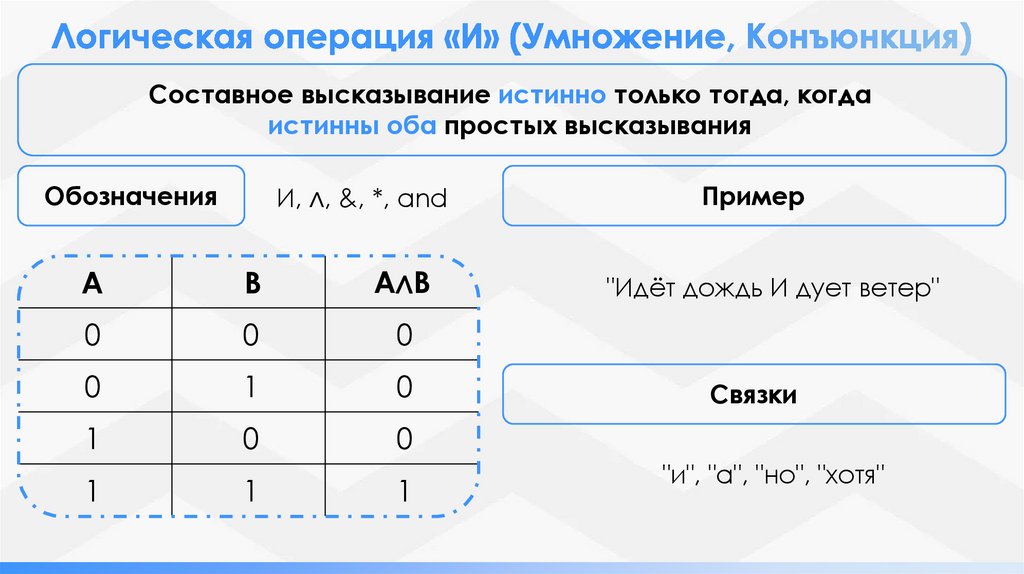
Составное высказывание истинно только тогда, когда
истинны оба простых высказывания
Обозначения
И, ∧, &, *, and
A
B
A∧B
0
0
0
0
1
0
1
0
0
1
1
1
Пример
"Идёт дождь И дует ветер"
Связки
"и", "а", "но", "хотя"

7.

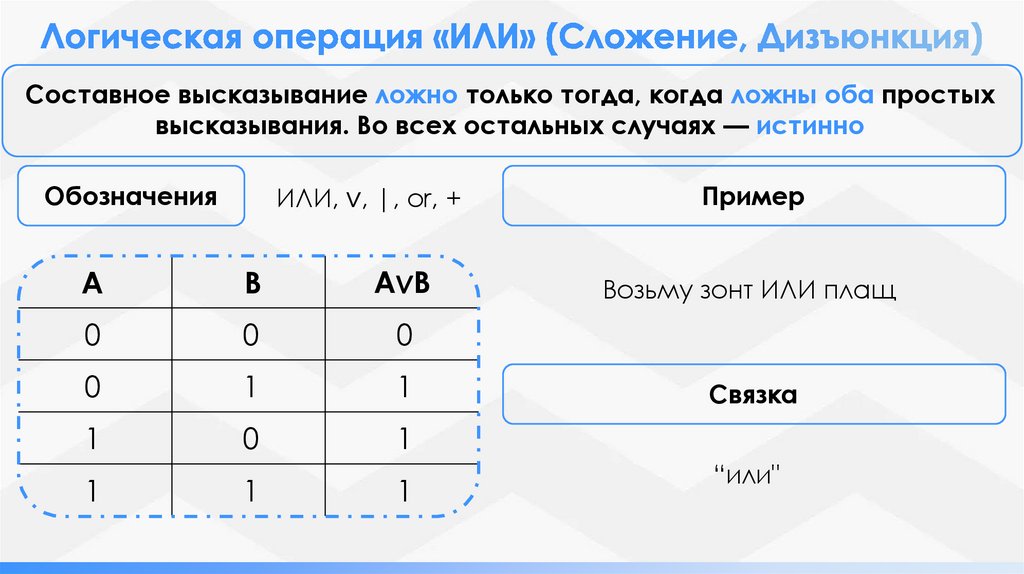
Составное высказывание ложно только тогда, когда ложны оба простых
высказывания. Во всех остальных случаях — истинно
Обозначения
ИЛИ, ∨, |, or, +
A
B
A∨B
0
0
0
0
1
1
1
0
1
1
1
1
Пример
Возьму зонт ИЛИ плащ
Связка
“или"

8.

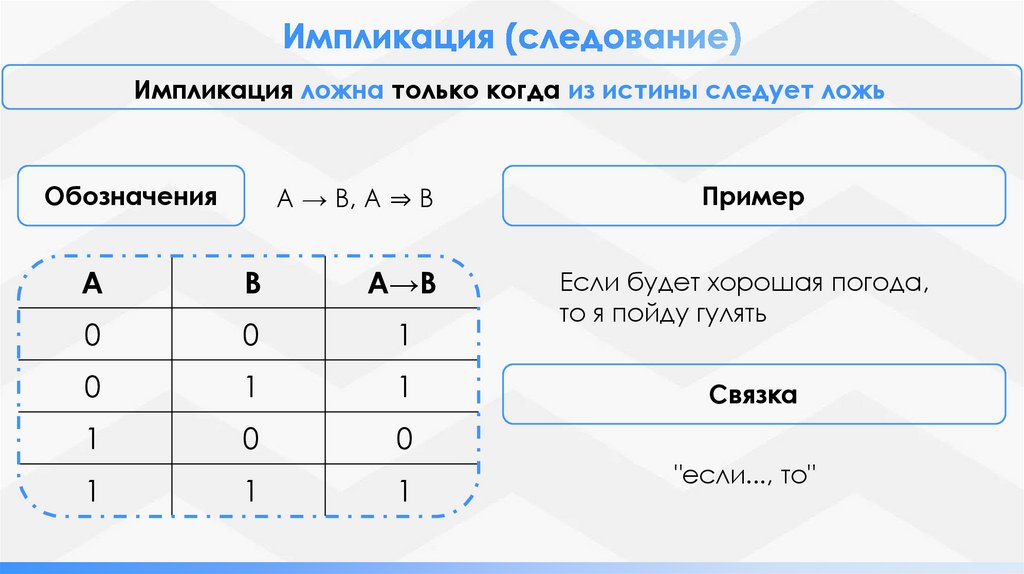
Импликация ложна только когда из истины следует ложь
Обозначения
A → B, A ⇒ B
A
B
A→B
0
0
1
0
1
1
1
0
0
1
1
1
Пример
Если будет хорошая погода,
то я пойду гулять
Связка
"если..., то"

9.

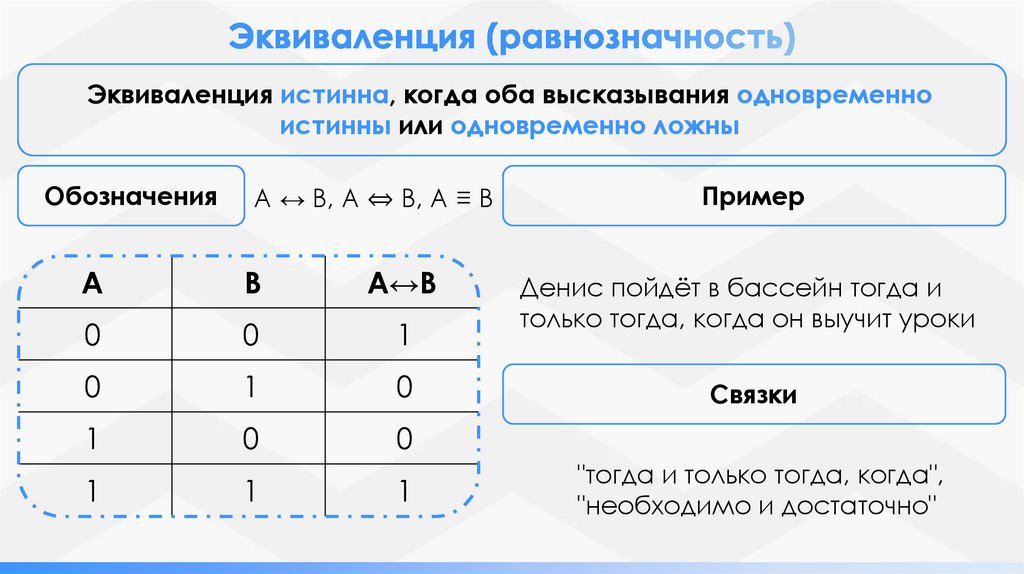
Эквиваленция истинна, когда оба высказывания одновременно
истинны или одновременно ложны
Обозначения
A ↔ B, A ⇔ B, A ≡ B
A
B
A↔B
0
0
1
0
1
0
1
0
0
1
1
1
Пример
Денис пойдёт в бассейн тогда и
только тогда, когда он выучит уроки
Связки
"тогда и только тогда, когда",
"необходимо и достаточно"

10.

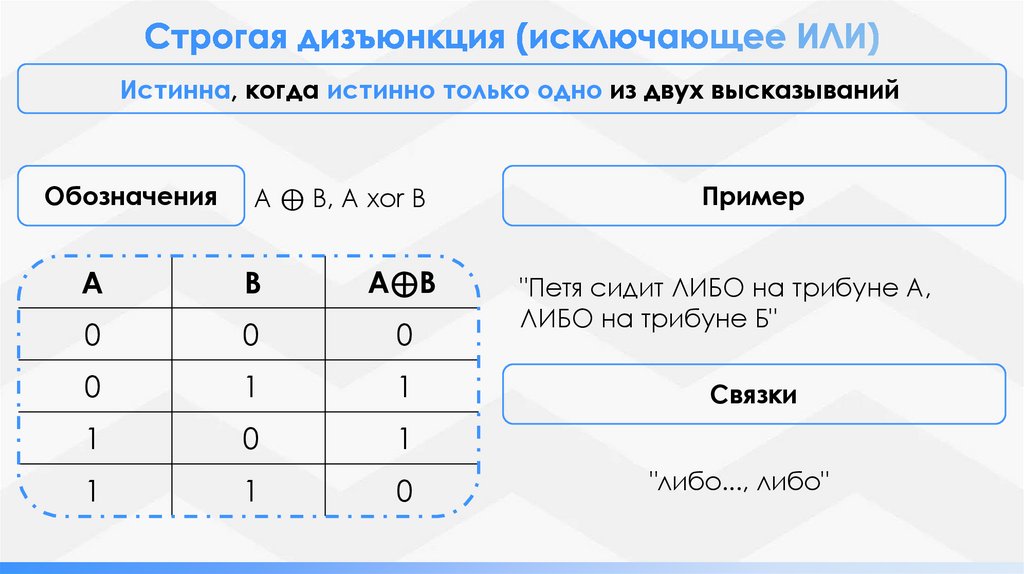
Истинна, когда истинно только одно из двух высказываний
Обозначения
A ⊕ B, A xor B
A
B
A⊕B
0
0
0
0
1
1
1
0
1
1
1
0
Пример
"Петя сидит ЛИБО на трибуне А,
ЛИБО на трибуне Б"
Связки
"либо..., либо"

11.

Порядок выполнения операций:
1. Отрицание (¬)
2. Конъюнкция (&)
3. Дизъюнкция (∨), строгая дизъюнкция (⊕)
4. Импликация (→), эквиваленция (↔)
Скобки меняют порядок выполнения операций!

12.

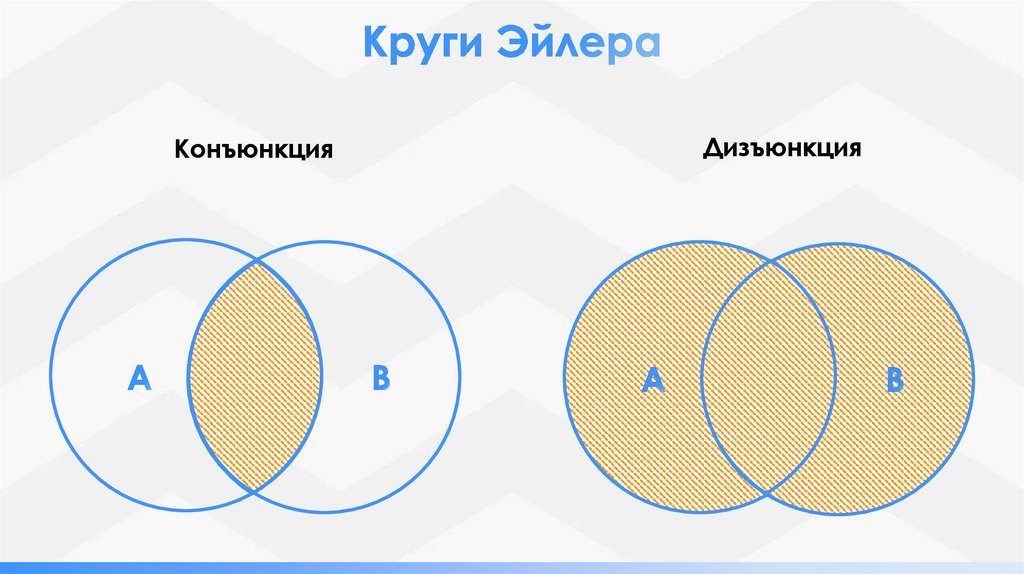
Конъюнкция
Дизъюнкция

13.

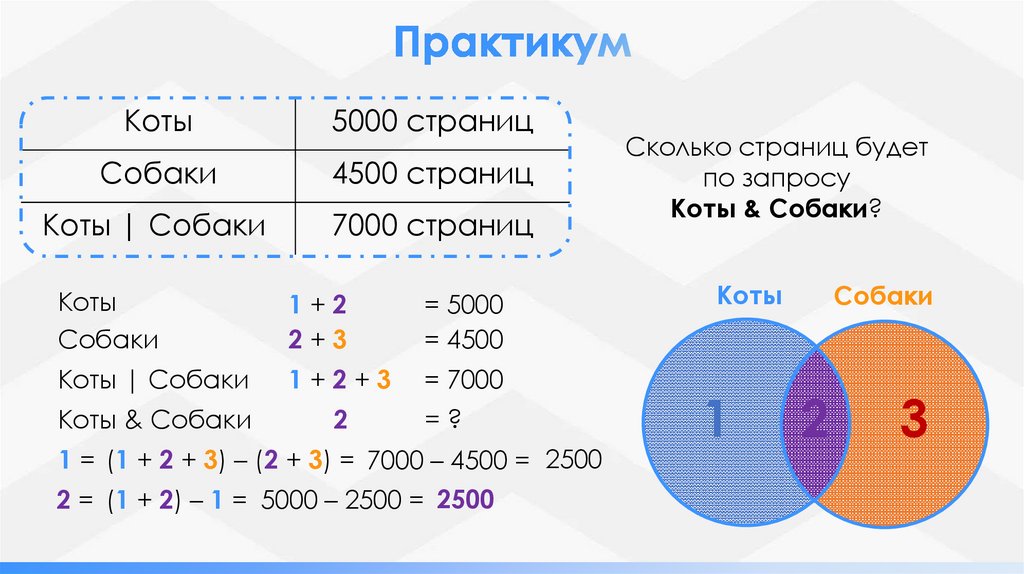
Коты
5000 страниц
Собаки
4500 страниц
Коты | Собаки
7000 страниц
Коты
Собаки
1+2
2+3
= 5000
= 4500
Коты | Собаки
1+2+3
= 7000
Коты & Собаки
2
=?
1 = (1 + 2 + 3) – (2 + 3) = 7000 – 4500 = 2500
2 = (1 + 2) – 1 = 5000 – 2500 = 2500
Сколько страниц будет
по запросу
Коты & Собаки?
Коты
1
Собаки
2
3

14.

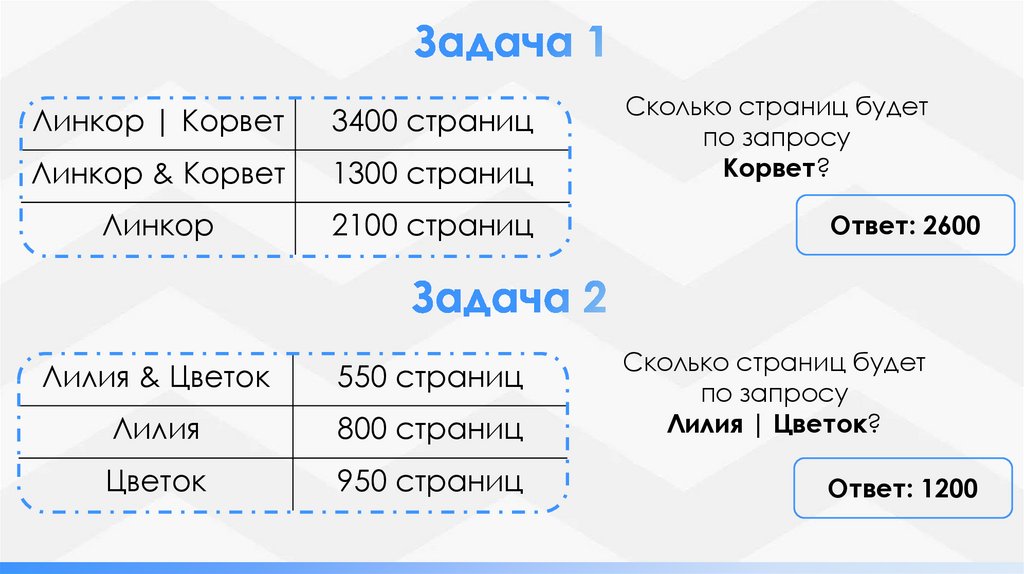
Линкор | Корвет
3400 страниц
Линкор & Корвет
1300 страниц
Линкор
2100 страниц
Лилия & Цветок
550 страниц
Лилия
800 страниц
Цветок
950 страниц
Сколько страниц будет
по запросу
Корвет?
Ответ: 2600
Сколько страниц будет
по запросу
Лилия | Цветок?
Ответ: 1200