Презентация на тему Решение текстовых задач на сплавы,смеси и на проценты

1.

МБУ «Школа №70»
Подготовка к ЕГЭ.
Решение текстовых задач на сплавы и смеси,
на проценты.
Морозова М.А.
Учитель математики

2.

Имеются сплавы золота и серебра. В одном эти металлы
находятся в отношении 2: 3, а в другом в отношении 3: 7.
Сколько нужно взять от каждого сплава, чтобы получить
1 кг нового, в котором золото и серебро находились бы в
отношении 5: 11?
Золото: Серебро = 2: 3
Золото: Серебро = 3: 7
Х кг
У кг
Золото: Серебро = 5: 11
По этой схеме уравнение х + у =1 показывает массу нового сплава.
Определяем массу золота в каждом сплаве и получаем уравнение
3
5
2
*х
+
*
у
=
*1
10
5
16
Аналогично массу серебра и получаем уравнение
7
11
3
*
х
+
*
у
=
10
5
16 * 1
Записываем одну из систем:
х+у=1
5
3
2
х
+
у
=
16
10
5
х+у=1
7
11
3
х
+
у
=
10
5
16
Решая ее, получаем х = 0,125 и у = 0,875
Ответ: 125 г и 875 г.

3.

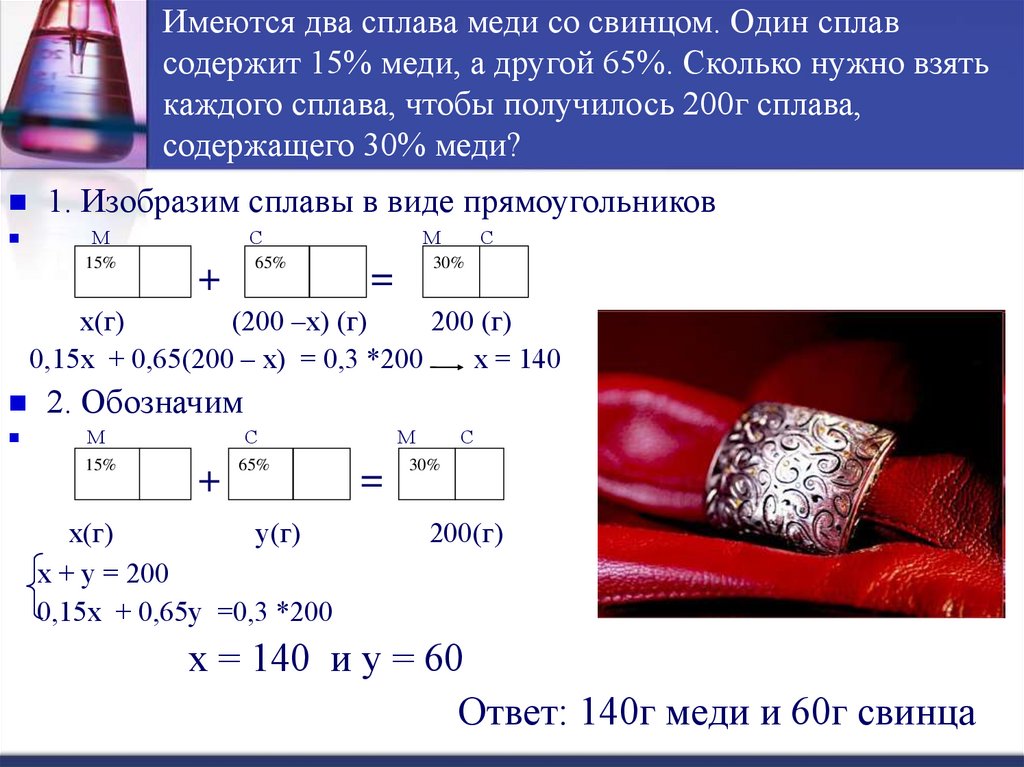
Имеются два сплава меди со свинцом. Один сплав
содержит 15% меди, а другой 65%. Сколько нужно взять
каждого сплава, чтобы получилось 200г сплава,
содержащего 30% меди?
1. Изобразим сплавы в виде прямоугольников
М
С
М
15%
65%
30%
+
=
С
х(г)
(200 –х) (г)
200 (г)
0,15х + 0,65(200 – х) = 0,3 *200
х = 140
2. Обозначим
М
С
М
15%
65%
30%
+
х(г)
у(г)
х + у = 200
0,15х + 0,65у =0,3 *200
=
С
200(г)
х = 140 и у = 60
Ответ: 140г меди и 60г свинца

4.

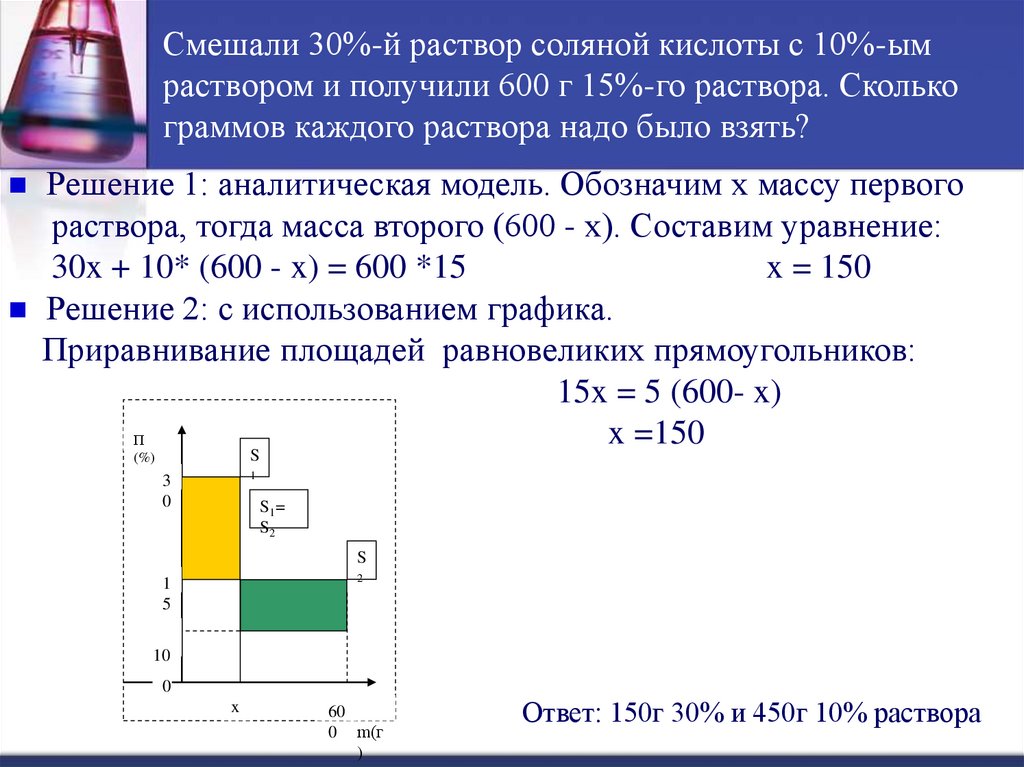
Смешали 30%-й раствор соляной кислоты с 10%-ым
раствором и получили 600 г 15%-го раствора. Сколько
граммов каждого раствора надо было взять?
Решение 1: аналитическая модель. Обозначим x массу первого
раствора, тогда масса второго (600 - x). Составим уравнение:
30x + 10* (600 - x) = 600 *15
x = 150
Решение 2: с использованием графика.
Приравнивание площадей равновеликих прямоугольников:
15x = 5 (600- x)
x =150
П
S
(%)
1
3
0
S1=
S2
S
2
1
5
10
0
x
60
0 m(г
)
Ответ: 150г 30% и 450г 10% раствора

5.

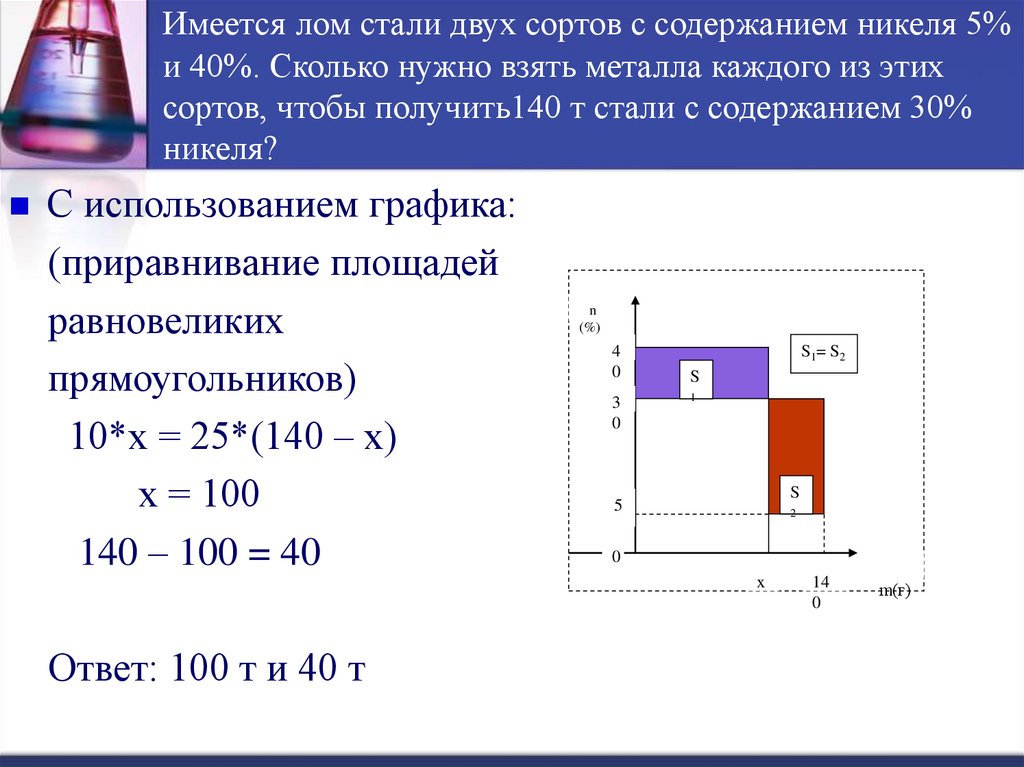
Имеется лом стали двух сортов с содержанием никеля 5%
и 40%. Сколько нужно взять металла каждого из этих
сортов, чтобы получить140 т стали с содержанием 30%
никеля?
С использованием графика:
(приравнивание площадей
равновеликих
прямоугольников)
10*х = 25*(140 – х)
х = 100
140 – 100 = 40
n
(%)
4
0
3
0
S1= S2
S
1
S
5
2
0
x
Ответ: 100 т и 40 т
14
0
m(г)

6.

Имеется два кислотных раствора: один 20%, другой 30%.
Взяли 0,5 л первого и 1,5 л второго раствора и образовали
новый раствор. Какова концентрация кислоты в новом
растворе?
Так как первый раствор 20 % - й, то в нем 0,2 объема занимает
«чистая» кислота. Так как объем первого раствора равен 0,5л,
то в этом количестве содержится 0,2*0,5=0,1 л «чистой»
кислоты.
Аналогично во втором растворе будет содержаться
0,3*1,5=0,45л «чистой» кислоты.
При смешивании растворов получим 0,5+1,5=2л кислотного
раствора, в котором 0,1+0,45=0,55л «чистой» кислоты.
Отсюда следует, что концентрация кислоты в новом растворе
есть отношение 0,55:2=0,275, т.е.27,5%.
Ответ: концентрация кислоты в новом растворе 27,5%

7.

Имеется руда из двух пластов с содержанием меди 6%
и 11%. Сколько «бедной» руды надо взять, чтобы
получить при смешивании с «богатой» 20 т руды с
содержанием меди 8%?
Аналитическая модель:
Переведем проценты в дроби:
6%=0,06; 11%=0,11; 8%=0,08
Пусть надо взять х т «бедной» руды,
которая будет содержать 0,06х т меди,
а «богатой» руды надо взять (20-х) т,
которая будет содержать 0,11(20 - х) т
меди.
Так как получившиеся 20 т руды
будут содержать 20*0,08 т меди, то
получим уравнение:
0,06х + 0,11(20 - х) = 20*0,08.
Решив уравнение, получим х = 12.
Ответ: 12т руды с 6% содержанием меди

8.

Старинный способ решения задач
на смешивание двух веществ
У некоторого человека были на продажу масла двух сортов: одно
ценою 10 гривен за ведро, другое же 6 гривен за ведро.
Захотелось ему сделать из этих двух масел, смешав их, масло
ценою 7 гривен за ведро. Какие части этих двух масел нужно
взять, чтобы получить ведро масла ценою 7 гривен?
7
6
3
10
1
Из схемы делаем заключение, что дешевого масла
нужно взять втрое больше, чем дорогого, т.е. для
получения одного ведра ценою 7 гривен нужно взять
дорогого масла 1/4 ведра, а дешевого масла 3/4.

9.

Способ Л.Ф.Магницкого для трех
веществ
Некто имеет чай трех сортов –цейлонский по 5 гривен за фунт,
индийский по 8 гривен за фунт и китайский по 12 гривен за фунт.
В каких долях нужно смешать эти сорта, чтобы получить чай
стоимостью 6 гривен за фунт?
5
6
12
5
6
2/8
1
2
1
8
1
1/10
6
6
Взять 6+2=8 частей чая ценой по 5 гривен и по
одной части ценой 8 гривен и 12 гривен за один фунт.
Возьмем 8/10 фунта чая ценой по 5 гривен за фунт и
по1/10 фунта чая ценой 8 и 12 гривен за фунт, то
получим 1 фунт чая ценой
8/10*5 + 1/10*8 + 1/10*12 = 6 гривен

10.

Сплавили два слитка серебра:
75 г 600-й и 150 г 864-й пробы.
Определить пробу сплава.
Пусть проба сплава равна х.
Составим диагональную схему:
Получаем:
(864 – х) : (х – 600) = 75 : 150
1728 – 2х = х – 600
х = 776.
Ответ: сплав 776-й пробы.

11.

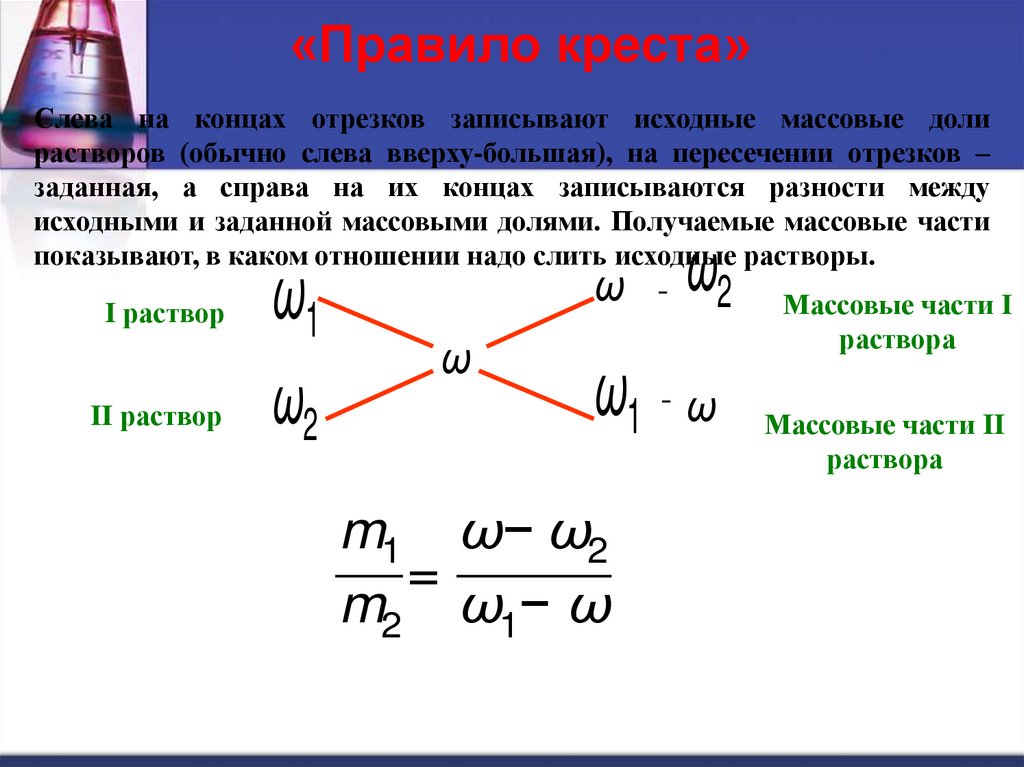
«Правило креста»
Слева на концах отрезков записывают исходные массовые доли
растворов (обычно слева вверху-большая), на пересечении отрезков –
заданная, а справа на их концах записываются разности между
исходными и заданной массовыми долями. Получаемые массовые части
показывают, в каком отношении надо слить исходные растворы.
I раствор
II раствор
ω1
ω2
ω
ω
-
ω2
ω1 - ω
m1 ω− ω2
=
m2 ω1− ω
Массовые части I
раствора
Массовые части II
раствора

12.

Задача: В 100г 20%-ного раствора соли
добавили 300г её 10%-ного раствора.
Определите процентную концентрацию
раствора.
0,2
Решение:
Х-0,1
х
0,1
0,2-х
1:3=(х-0,1):(0,2-х);
Х=0,125; х=12,5%.
Ответ: х=12,5%.

13.

Задача: В 100г 20%-ного раствора соли добавили
300г её 10%-ного раствора. Определите
процентную концентрацию раствора.
m1=100г
с помощью расчетной формулы
m2=300г
ω1= 0,2
ω1 m1+ω2 m2
0,2⋅100+0,1⋅ 300
ω2= 0,1 ω=
= 0,125
m1+m2 ω=
ω= ?
100+300
Ответ: 12,5%

14.

ω1 ,%
Массовые
доли
ω1
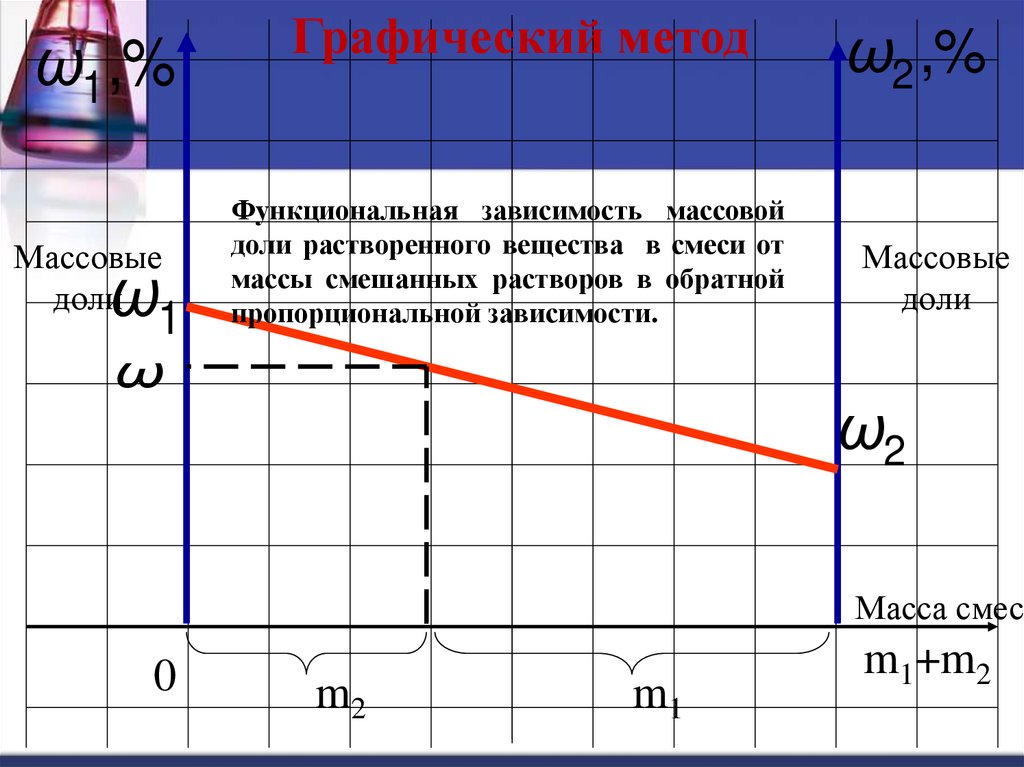
Графический метод
Функциональная зависимость массовой
доли растворенного вещества в смеси от
массы смешанных растворов в обратной
пропорциональной зависимости.
ω
ω2 ,%
Массовые
доли
ω2
Масса смеси
0
m2
m1
m1+m2

15.

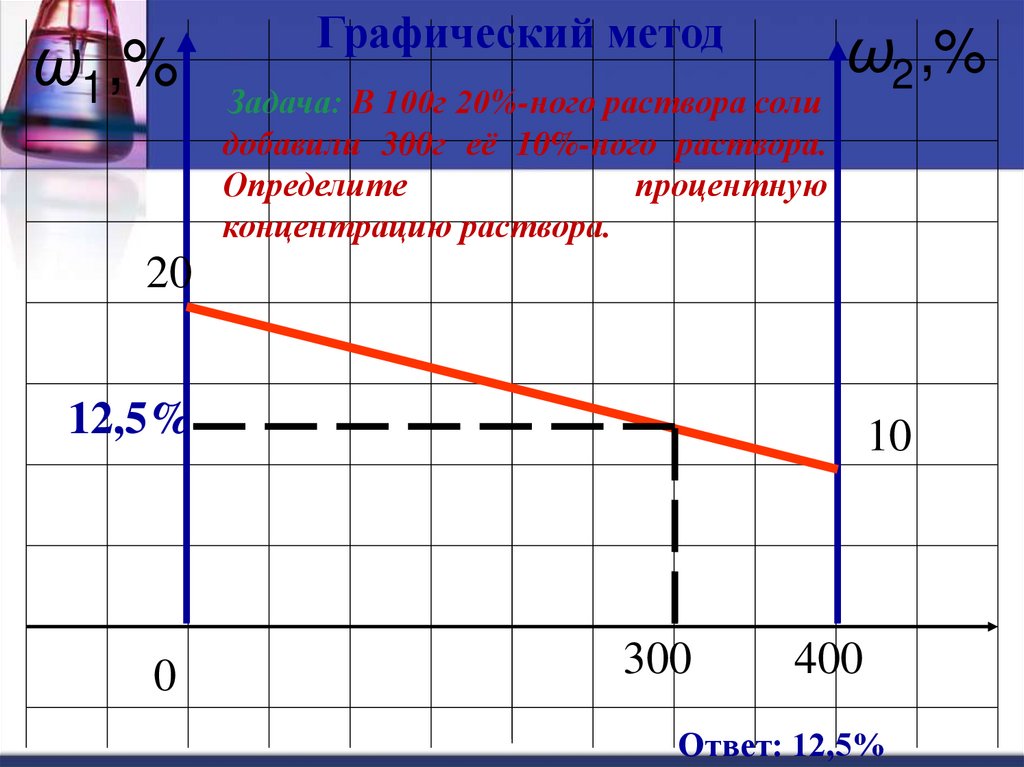
ω1 ,%
Графический метод
Задача: В 100г 20%-ного раствора соли
добавили 300г её 10%-ного раствора.
Определите
процентную
концентрацию раствора.
ω2 ,%
20
12,5%
0
10
300
400
Ответ: 12,5%

16.

От двух кусков сплава с массами 3 кг и 2 кг и с концентрацией меди
0,6 и 0,8 отрезали по куску равной массы. Каждый из отрезанных
кусков сплавлен с остатком другого куска, после чего концентрация
меди в обоих сплавах стала одинаковой. Какова масса каждого из
отрезанных кусков?
Обозначим массу отрезанного куска х (кг).
Так как в обоих сплавах концентрация меди после двух операция
стала одинаковой, то массы сплавов и массы меди в этих сплавах
пропорциональны.
Первоначально массы меди в сплавах равны 0,6*3(кг) и 0,8*2(кг).
После того, как отрезали куски массой х(кг), содержание меди
стало 0,6(3-х) и 0,8(2-х), а после сплавления
mм(кг)
0,6(3-х) + 0,8х и 0,8(2-х) +0,6х
1,8+0,3х
1,6-0,2х
1,8+0,2х 3
1,6− 0,2 х = 2 , х = 1,2
2
Ответ: 1,2 кг
3
mc(кг)

17.

Латунь – сплав меди и цинка. Кусок латуни содержит меди на 11
кг больше, чем цинка. Этот кусок латуни сплавили с 12 кг меди и
получили латунь, в котором 75% меди. Сколько килограммов меди
было в куске латуни первоначально?
Обозначим искомую величину за х.
Тогда масса первоначального куска латуни 2х – 11, а
х
его содержание меди составляет р = 100
процентов.
2х− 1
Поскольку «медность» куска меди 100%, то по правилу
квадрата получаем:
р
25
25
= 2х− 11 , х = 22,5
75− р
75
100
12
75 - р
Ответ: 22,5 кг меди было в куске латуни.

18.

В бидон налили 4л молока трехпроцентной жирности и
6л молока шестипроцентной жирности. Сколько
процентов составляет жирность молока в бидоне?
Обозначим искомую величину за Х.
По правилу квадрата получим:
6-х
3
х
6
х-3
Составим пропорцию:
4
6− х
= , х = 4,8
х− 3
6
Ответ: 4,8 % - жирность молока.

19.

Формула Простых
ПРОЦЕНТОВ
S =α(1+ t p/m)
S - итоговая сумма;
α - начальная стоимость кредита;
t - срок кредита;
p - годовая процентная ставка;
m – количество дней в году;
Ежемесячный платеж :
Sкредит = S /12 t,
где Sкредит – сумма гашения кредита,
S – размер кредита,
t – срок кредитования,
Sкредит = const.

20.

Формула сложных процентов
S = K ∙ (1+P∙d/D/100)ⁿ
S – сумма депозита с процентами;
K – сумма депозита (капитал);
P- годовая процентная ставка;
d – количество дней начисления
процентов по привлеченному вкладу;
D – количество дней в календарном году;
n - число периодов начисления процентов;
Нельзя сегодня людям без
знаний процентов!

21.

Задача 1.
Какая сумма будет на счете вкладчика
через 5 лет, если банк начисляет 20%
годовых и внесенная сумма равна
500 000р.?
Решение:
Через 5 лет сумма составит:
(1 + 20/100)5 · 500 000 = 1 244 160 (р.)

22.

Задача 2
За переадресацию вклада банком установлены
комиссионные в размере 0,2% от суммы вклада. Вклад
на сумму 100 000 р. был переадресован
3 раза. На сколько уменьшился вклад?
Решение: Воспользуемся формулой:
Sn = (1 – p/100) n · S, где S = a; Sn = х; n = t.
S3 = (1 – 0,2/100)3 · 100 000 = 99 401,19(р.)
Значит, уменьшение составило:
100 000 – 99 401,19 = 598,81 (р.)

23.

Примеры задач «на проценты»:
1) Цена изделия составляла 1000 рублей и была снижена
сначала на 10%, а затем еще на 20%. Какова
окончательная цена товара?
Решение:
10% = 0,1; 20% = 0,2.
0,1 · 1000 = 100 (р.) – составило первое снижение
1000 – 100 = 900 (р.) – цена товара после первого
снижения
0,2 · 900 = 180 (р.) – составило второе снижение
900 – 180 = 720 (р.) – цена товара после второго снижения
Ответ: 720.

24.

2) Цену товара повысили на 25%, затем новую цену повысили еще на 10% и,
наконец, после перерасчета произвели повышение цены еще на 12%. На
сколько процентов повысили первоначальную цену товара?
Решение: Пусть первоначальная цена товара – х р.
Тогда после повышения цены товара на 25% она стала:
х + 0,25х = 1,25х (р.)
После повышения цены товара на 10% она стала:
1,25х + 0,1 · 1,25х = 1,25х + 0,125х = 1,375х (р.)
После повышения цены товара на 12% она стала:
1,375х + 0,12 · 1,375х = 1,375х + 0,165х = 1,54х (р.)
В целом, цена товара была повышена на 1,54х – х = 0,54х, что
составило 54% от первоначальной цены.
Ответ: 54

25.

3) Найдите первоначальную сумму вклада (в рублях), если после
истечения двух лет она выросла на 304,5 рубля при 3% годовых.
Решение: Пусть S – первоначальная сумма вклада. Тогда
через два года она составит :
S2 = (1 + 3/100) 2 · S
Т.к. S2 > S на 304,5, то уравнение имеет вид:
(1 + 3/100) 2 · S = S + 304,5;
1,032 · S = S + 304,5;
1,0609S – S = 304,5;
0,0609S = 304,5;
S = 304,5/0,0609;
S = 5000
Ответ: 5000.

26.

Четыре рубашки дешевле куртки на 8%. На
сколько процентов пять рубашек дороже
куртки?
b - стоимость куртки
4a < на 8%, т.е. составляет 0,92 части от b
4a = 0,92b /:4
Пусть
4a - стоимость 4-х рубашек
a = 0,23b
Найдем процентное отношение стоимости 5 рубашек к стоимости куртки
5⋅ 0, 23 b
5a
⋅ 100%= 5⋅ 0,23⋅ 100%=
⋅ 100%=
b
b
= 5⋅ 23= 115% Ответ: 5 рубашек дороже куртки 15%

27.

ЗАДАЧА НА ВЫСУШИВАНИЕ.
Виноград содержит 90% влаги, а изюм — 5%. Сколько
килограммов винограда требуется для получения
50
килограммов изюма?
Сухое
вещество
Влага
Виноград
10%
90%
Изюм
95% =0,95
5%
Сколько сухого вещества
в 20 кг изюма?
это 19 кг
50 кг изюма
1) 50 · 0,95 = 47,5 (кг) сухого вещества в изюме
47,5 кг сухого в-ва в винограде составляет 10% всего
винограда
2) 47,5 · 10 = 475 (кг) винограда надо взять
Ответ: 475

28.

Приложение
1.Сплавили 2кг сплава цинка и меди, содержащего 20%
цинка, и 6кг сплава цинка и меди, содержащего 40%
цинка. Найдите процентную концентрацию меди в
получившемся сплаве.
Ответ: 65% меди.
2. Для приготовления маринада необходим
2% раствор уксуса. Сколько нужно добавить
воды в 100г 9%-го раствора уксуса, чтобы получить
раствор для маринада?
Ответ: 350 г воды

29.

3. Имеются два сплава, в одном из которых содержится 20%, в другом 30%
олова. Сколько нужно взять первого и второго сплава, чтобы получить 10
кг нового сплава, содержащего 27% олова?
Ответ: 3 кг , 7 кг.
4. Имеются два сплава, в одном из которых содержится 40%, а во втором 20%
серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы
получить сплав, содержащий 32% серебра?
5. Имеются два сплава, в одном из которых содержится 10%, а в другом –
20% меди. Сколько нужно взять первого и второго сплавов, чтобы
получить 15 кг нового сплава, содержащего 14% меди?
Ответ: 9 кг и 6 кг.
6. Имеются два сплава, в одном из которых содержится 30%, а в другом –
50% золота. Сколько кг второго сплава нужно добавить к 10 кг первого,
чтобы получить сплав, содержащий 42% золота?
Ответ: 15 кг.

30.

7. Из молока, жирность которого 5%, делают творог, жирностью 0,5%.
Определить, сколько творога получается из 1 тонны молока?
Ответ: 300 кг.
8. При смешивании растворов, содержащих 25% и 60% кислоты, получился
раствор, содержащий 39% кислоты. Определить в какой пропорции были
смешаны растворы?
Ответ: 3 : 2.
9. Добытая руда содержит 21% меди, а обогащенная – 45%. Известно, что в
процессе обогащения 60% добытой руды идет в отходы. Определить
процентное содержание меди в отходах.
Ответ: 5%.
10. В 100 граммов 20%-ного раствора соли добавили 300 граммов ее 10%ного раствора. Определить концентрацию полученного раствора.
Ответ: 12,5%.

31.

«Только из союза двоих, работающих вместе и
при помощи друг друга, рождаются великие
вещи».
Антуан Де Сент-Экзюпери
«При единении и малое растет, при раздоре и
величайшее распадается». Саллюстий Гай Крисп