+Апории Зенона и современная наука (нормальный бег) с видео

1.

АПОРИИ ЗЕНОНА
И СОВРЕМЕННАЯ НАУКА
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026
КИРИН Николай Александрович
кандидат физико-математических наук, доцент

2. ПЛАН ДОКЛАДА:

1. Элейская школа (Парменид и Зенон)
2. Парадоксы Зенона
3. Современные взгляды на апории Зенона
Докладчик
КИРИН
Николай Александрович
кандидат физико-математических
наук, доцент

3.

Апории Зенона
Современный взгляд и нерешенные
проблемы
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

4. Элейская школа Иллюзорность изменчивости

Элея
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

5. Элейская школа Иллюзорность изменчивости

Парменид
Зенон
(ок. 540 до н.э. – ок. 470 до н.э.)
(ок. 490 до н.э. – ок. 430 до н.э.)
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

6. Элейская школа Иллюзорность изменчивости

Движение
Движенья нет, сказал мудрец брадатый.
Другой смолчал и стал пред ним ходить.
Сильнее бы не мог он возразить;
Хвалили все ответ замысловатый.
Но, господа, забавный случай сей
Другой пример на память мне приводит:
Ведь каждый день пред нами солнце ходит,
Однако ж прав упрямый Галилей.
А.С. Пушкин (1821 г.)
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

7. Элейская школа Иллюзорность изменчивости

Парменид: мир как единое, вечное и неизменное бытие
Парадоксы Зенона: обоснование элейской онтологии
Апория места (немыслимость пустоты)
Апории множества (немыслимость множества)
Парадокс делимости
Парадокс сложения
Парадокс счисления
Апории движения (немыслимость движения)
«Ахилл и черепаха»
«Дихотомия» (деление на два)
«Стрела»
«Стадий»
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

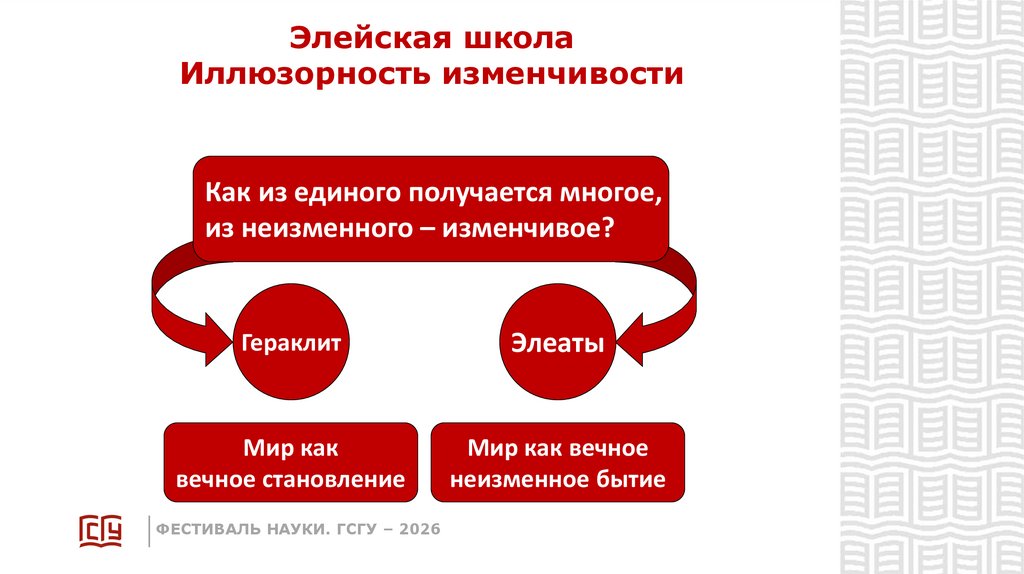
8. Элейская школа Иллюзорность изменчивости

Как из единого получается многое,
из неизменного – изменчивое?
Гераклит
Элеаты
Мир как
вечное становление
Мир как вечное
неизменное бытие
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

9. Парадоксы Зенона Обоснование элейской онтологии

Апория места (немыслимость пустоты)
Апории множества (немыслимость множества)
Парадокс делимости
Парадокс сложения
Парадокс счисления
Апории движения (немыслимость движения)
«Ахилл и черепаха»
«Дихотомия» (деление на два)
«Стрела»
«Стадий»
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

10. Парадоксы Зенона Обоснование элейской онтологии

Апорúя
(греч. απορία, затруднение, безвыходное положение;
от α, отрицательная приставка, и πόρος, выход) –
понятие древнегреческой философии, обозначающее
трудноразрешимую или неразрешимую проблему.
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

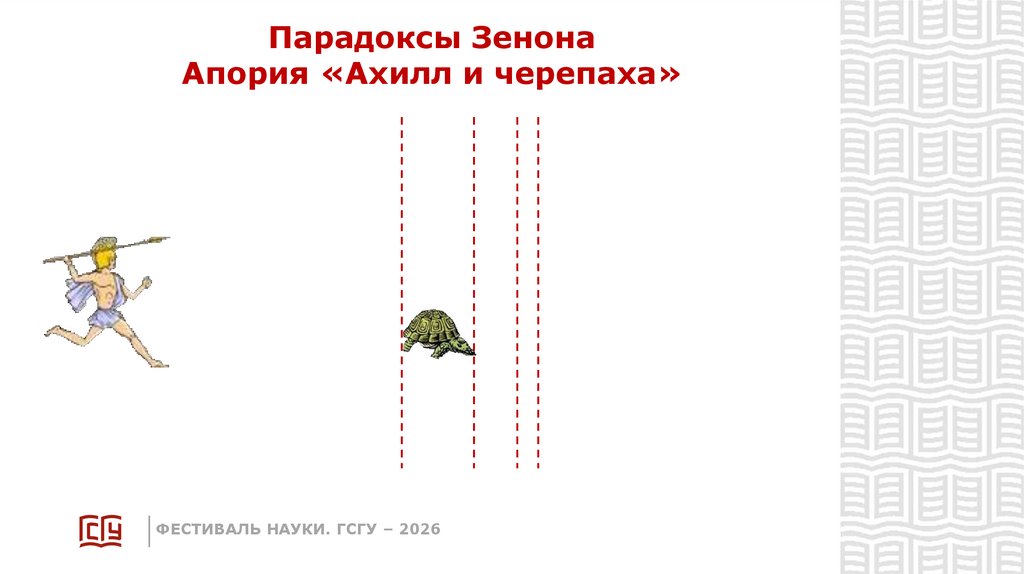
11.

Парадоксы Зенона
Апория «Ахилл и черепаха»
Быстроногий Ахилл
никогда не догонит
медленно ползущую черепаху.
Ведь прежде, чем догнать её, он
должен будет дойти до того места,
в котором она находилась,
когда он за ней погнался.
Но за это время черепаха
уйдёт вперёд и, таким образом,
опять окажется впереди Ахилла,
и так далее до бесконечности.
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

12.

Парадоксы Зенона
Апория «Ахилл и черепаха»
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

13.

Парадоксы Зенона
Апория «Ахилл и черепаха»
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

14.

Парадоксы Зенона
Апория «Дихотомия»
Дuхотомúя
(греч. διχοτομία; от δίχα, на две части,
и τομή, сечение, разделение) –
1) Деление целого на две части (с последующим
делением каждой из частей на две подчасти и т.д.);
2) Метод классификации, состоящий в делении объёма
понятия (класса, множества) на два подчинённых
взаимоисключающих (противоречащих) понятия,
суммарный объём которых исчерпывает объём
делимого понятия.
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

15.

Парадоксы Зенона
Апория «Дихотомия»
Ахилл вообще
не сдвинется с места
(как, впрочем, и черепаха),
так как прежде, чем
добраться до любого места,
он должен пройти то место,
которое находится на полпути
между ним и первым местом,
а прежде, чем пройти это
второе место, он должен пройти
место, которое находится
на полпути между ними,
и так далее до бесконечности.
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

16.

Парадоксы Зенона
Апория «Дихотомия»
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

17.

«Ахилл и черепаха»
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

18.

«Ахилл и черепаха»
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

19.

«Ахилл и черепаха»
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

20.

«Ахилл и черепаха»
В основе лежит представление о бесконечности
суммы бесконечного количества слагаемых.
Известный в математике «Принцип Архимеда»
применен некорректно.
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

21.

Парадоксы Зенона
Апория места
Если условием существования
является нахождение в каком-то месте,
то и само место, коль скоро оно существует,
тоже должно находиться в каком-то месте.
Это будет уже «второе» место, но и оно
должно существовать в каком-то «третьем»
месте, и так далее до бесконечности.
Следовательно, «пустое место»,
как что-то отличное от того,
местом чего оно является, немыслимо.
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

22.

Парадоксы Зенона
Апория «Стрела»
Стрела не может лететь
ни там, где её нет,
ни там, где она есть.
Она ведь занимает в пространстве
место, равное своему размеру –
ни больше, ни меньше
(иначе она была бы больше
или меньше себя самой).
Так как в этом месте ей двигаться
некуда, она покоится, а поскольку
это верно для любого отрезка её
траектории, она покоится всегда.
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

23.

Парадоксы Зенона
Апория «Стрела»
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

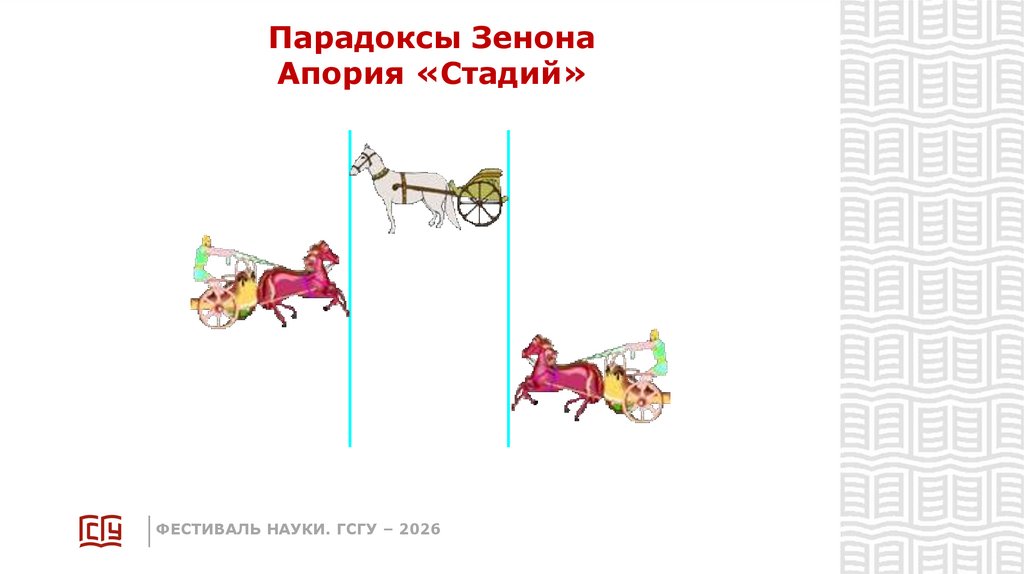
24.

Парадоксы Зенона
Апория «Стадий»
Если две колесницы движутся навстречу
друг друга со скоростью, равной
минимальной единице пространства
за минимальную единицу времени,
мимо третьей – неподвижной – колесницы,
то они пройдут расстояние, равное
минимальной единице пространства, за
минимальную единицу времени относительно
неподвижной колесницы и за половину минимальной
единицы времени относительно друг друга.
Таким образом, получится, что минимальная,
т.е. неделимая, единица времени делима,
что абсурдно. (Равным образом,
делимой окажется и минимальная,
т.е. неделимая, единица пространства).
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

25.

Парадоксы Зенона
Апория «Стадий»
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

26.

Элейская школа
Иллюзии восприятия и мыслимая реальность
Разум свидетельствует, что
ни пустоты, ни множества,
ни движения нет,
ибо они немыслимы.
Чувства не позволяют утверждать
существование пустоты, но
свидетельствуют о существовании
многих движущихся вещей.
У нас есть, таким образом,
два источника знания,
которые в чём-то
противоречат друг другу.
Какой же из них следует
признать достоверным?
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

27.

«Если условием существования является
нахождение в каком-то месте…»
Пространство воспринимается как «вместилище» в то время как
предметы сами создают пространство, поэтому существуя они
сами создают пространство, а не находясь в пространстве
«получают право» считаться существующими.
Возникает некоторая путаница понятий. Отождествляется
понятия «физического расположения» и «названия места».
Отрицание существования «пустого места» основано на
бездоказательном утверждении, что все должно что-либо
содержать в себе. При этом делается логическая ошибка,
так как даже, если допустить, что всё в чем-то содержится,
то из этого не следует, что «пустого места» не существует,
из этого лишь следует, что само «пустое место» где-то
расположено. Но, как известно, пустое множество является
подмножеством любого множества, следовательно, ни
каких противоречий нет.
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

28.

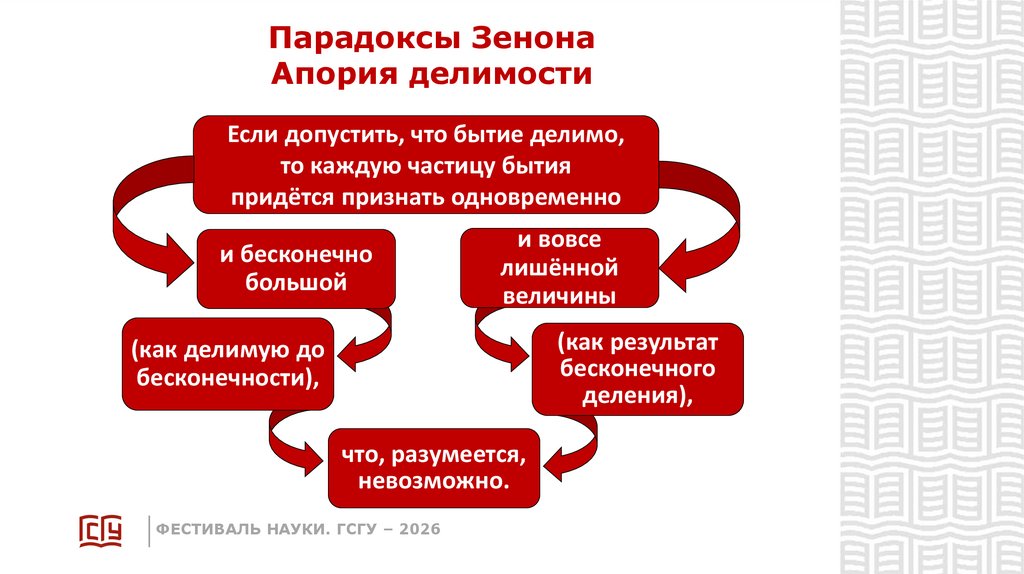
Парадоксы Зенона
Апория делимости
Если допустить, что бытие делимо,
то каждую частицу бытия
придётся признать одновременно
и бесконечно
большой
и вовсе
лишённой
величины
(как результат
бесконечного
деления),
(как делимую до
бесконечности),
что, разумеется,
невозможно.
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

29.

«Делимость в понимании Зенона не
Совпадает с современным подходом
Зенон считал, что целое состоит из того что, образуются в
результате его деления. Однако современная физика знает
обратные примеры. Например, если в результате ядерного распада
образуются некоторые частицы, то это не означает, что они входили
в состав распавшейся частицы, так как на самом деле они просто
создались за счет освободившейся энергии
Попытки установить или опровергнуть дискретность пространствавремени предпринимаются в современной науке по сей день. Пути
объединения квантовой механики и общей теории относительности
привела к предположению, что существуют ячейки пространствавремени с минимально возможной длиной
(фундаментальная длина)
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

30.

Согласно современной теории, если пространство дискретно, то
длина дискретных частей пространства равна планковской длине
Она равна менее триллионной части диаметра атома водорода. Для измерения объектов сравнимых с планковской длиной необходимо направить на
него поток фотонов с большой энергией, так как чем больше энергия фотонов,
тем меньше длина их волны.
Физик Роберт Немирофф из Мичиганского технологического университета
предложил использовать фотоны предельно высоких энергий и расстояние
рассеивания — в миллиарды световых лет.
Он обратился к результатам наблюдений космического гамма-телескопа
«Ферми». С его помощью были зарегистрированы серии гамма-фотонов
энергией более 1 ГэВ от источников GRB 080916C, GRB 090510A, GRB 090902B, и
GRB 090926A.
Анализ данных показал — если зернистость пространства вообще существует, то
она должна быть на уровне 10−48 метров или меньше. Пока подтверждений нет.
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

31.

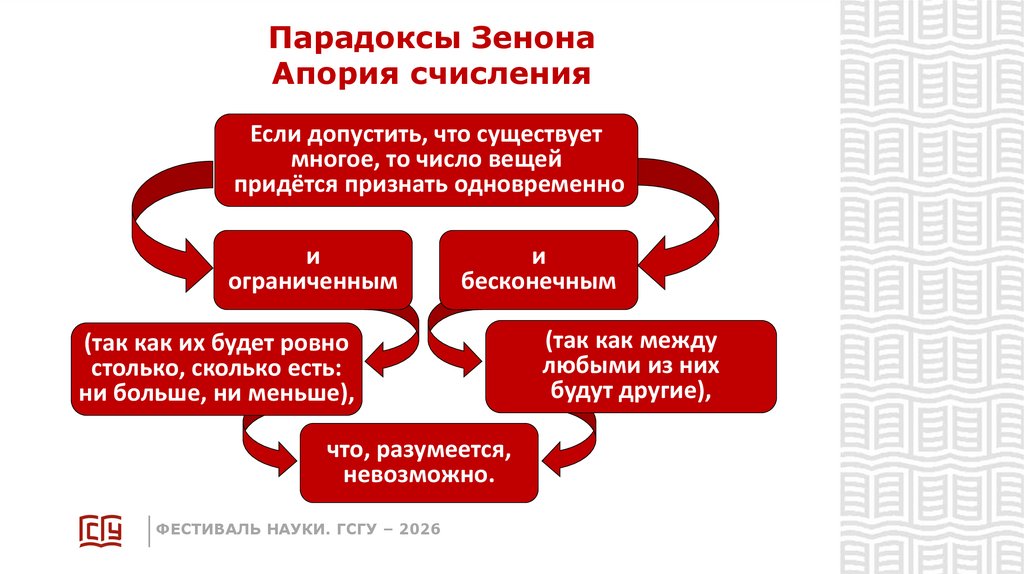
Парадоксы Зенона
Апория счисления
Если допустить, что существует
многое, то число вещей
придётся признать одновременно
и
ограниченным
и
бесконечным
(так как их будет ровно
столько, сколько есть:
ни больше, ни меньше),
что, разумеется,
невозможно.
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026
(так как между
любыми из них
будут другие),

32.

«Отсутствие сформированного понятия
о бесконечных (даже о счетных) множествах
В своих рассуждениях Зенон смешивает представления о материальных
предметах с представлениями о числовых множествах. Такая же ошибка
в представлении чисел была свойственна и греческим математикам, так
как, не смотря на постулирование «безразмерности» точек, всё равно,
например, точки прямой мыслились и моделировались как «камешки на
песке», со всеми вытекающими огрехами этой модели.
Отсутствие понятия о бесконечных множествах (даже о счетных), приводило
к тому, что признавая существования каких-либо объектов, автоматически
делался вывод о конечности их числа. В то время как уже для счетных множеств
неверно утверждение, что, если чисел бесконечно много, то между любыми
из них располагаются другие числа. Например, для множества рациональных
чисел это верно, а для множества натуральных чисел – нет.
ФЕСТИВАЛЬ НАУКИ. ГСГУ – 2026

33.

Σας ευχαριστώ για
την προσοχή σας
(Sas efcharistó gia tin prosochí sas)
GUKOLOMNA.RU