ЗАНЯТИЕ 1_2_ГРАФЫ_случ эксп

1. Элементы теории графов. Случайные события (Занятия 1-2)

БЕЖИНА И.Н.

2. Что общего в этих рисунках?

В математике есть специальный инструмент для изображения и изучения связей между
объектами. Это граф
(Слово «граф» происходит от латинского слова graphica «рисование, черчение»).

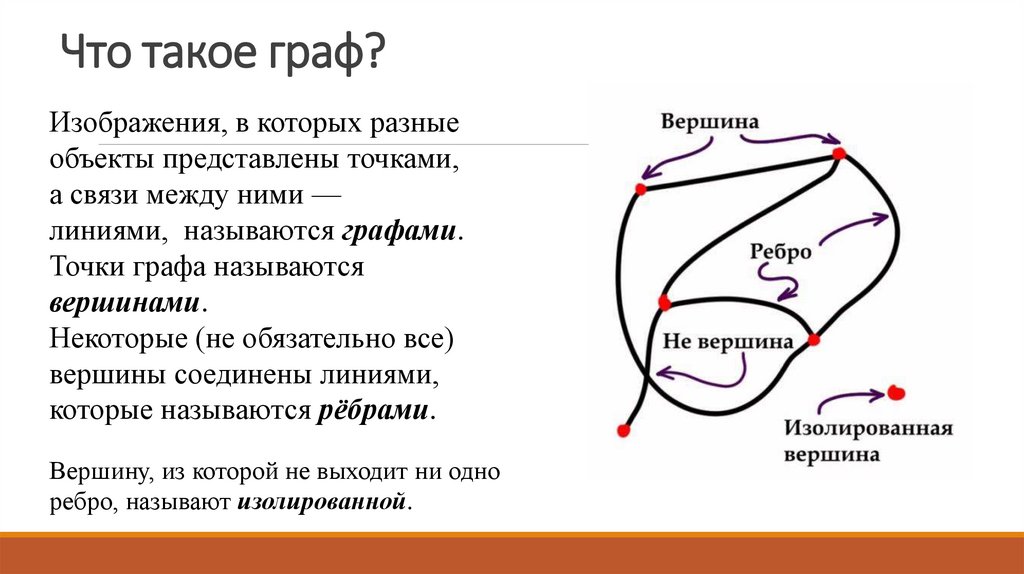
3. Что такое граф?

Изображения, в которых разные
объекты представлены точками,
а связи между ними —
линиями, называются графами.
Точки графа называются
вершинами.
Некоторые (не обязательно все)
вершины соединены линиями,
которые называются рёбрами.
Вершину, из которой не выходит ни одно
ребро, называют изолированной.

4.

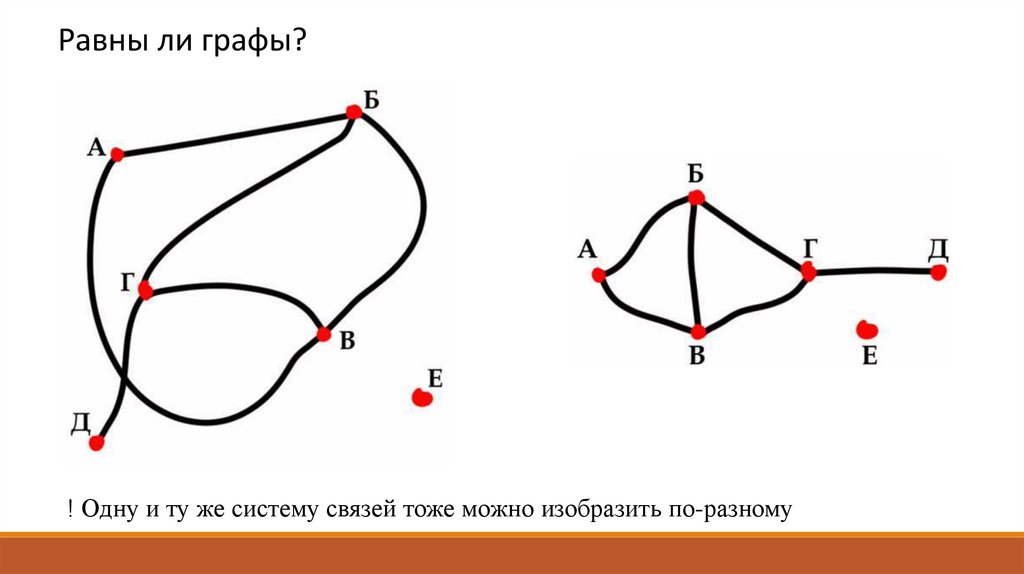
Равны ли графы?
! Одну и ту же систему связей тоже можно изобразить по-разному

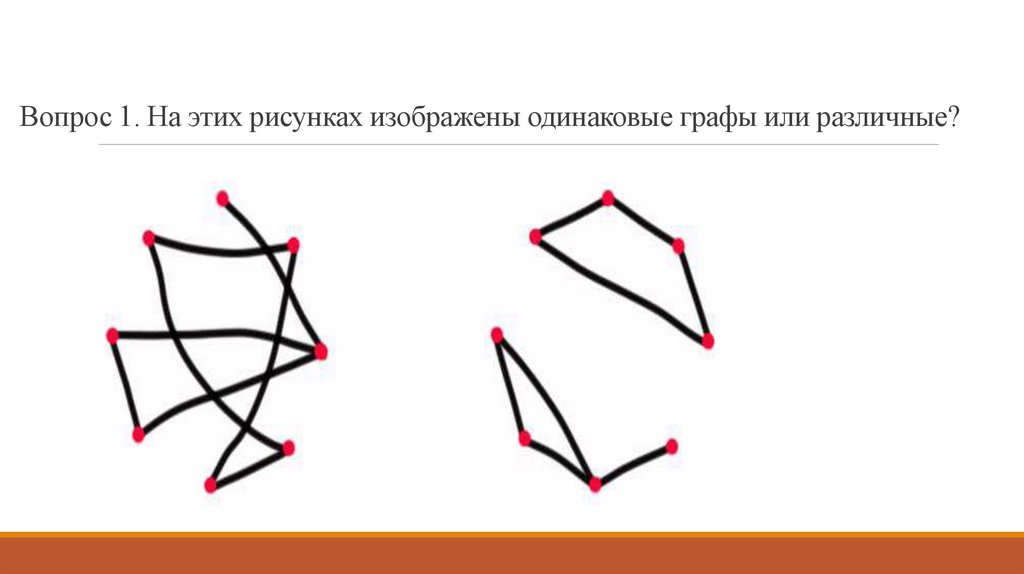
5. Вопрос 1. На этих рисунках изображены одинаковые графы или различные?

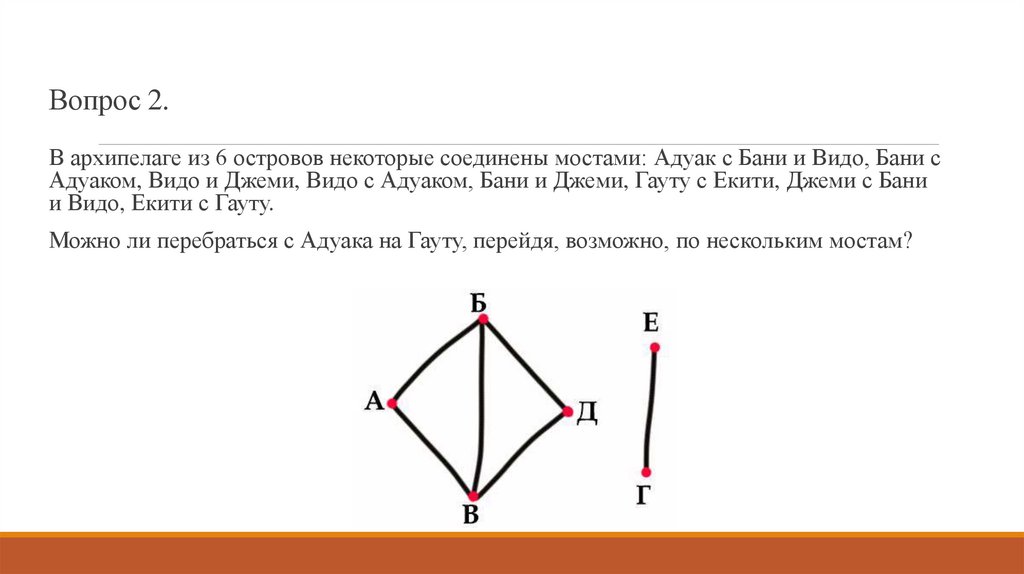
6. Вопрос 2.

В архипелаге из 6 островов некоторые соединены мостами: Адуак с Бани и Видо, Бани с
Адуаком, Видо и Джеми, Видо с Адуаком, Бани и Джеми, Гауту с Екити, Джеми с Бани
и Видо, Екити с Гауту.
Можно ли перебраться с Адуака на Гауту, перейдя, возможно, по нескольким мостам?

7. Вопрос 3.

Начало теории графов положил Леонард Эйлер, решая
задачу о семи мостах в г. Кёнигсберг. Сейчас это город
Калининград. Через город протекает река Преголя,
которую во времена Эйлера называли Прегель.
На рисунке представлен план Кенигсберга. Зеленым
цветом показаны мосты через реку. Можно ли пройти по
всем семи мостам, не проходя ни по одному дважды?
Эту задачу предложили Эйлеру Л. (1707-1783).
Эйлер решил эту задачу с помощью графа, хотя еще и не
использовал это слово. Нарисуйте граф для этой задачи.
а) Что изображают вершины? б) Что изображают ребра?
в) Как переформулировать задачу для графа?

8.

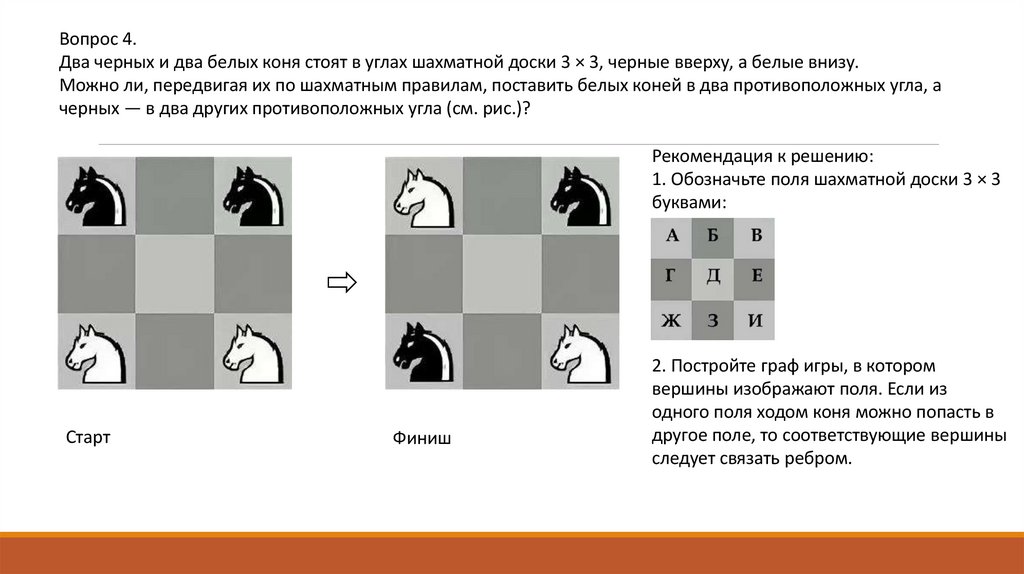
Вопрос 4.
Два черных и два белых коня стоят в углах шахматной доски 3 × 3, черные вверху, а белые внизу.
Можно ли, передвигая их по шахматным правилам, поставить белых коней в два противоположных угла, а
черных — в два других противоположных угла (см. рис.)?
Рекомендация к решению:
1. Обозначьте поля шахматной доски 3 × 3
буквами:
Старт
Финиш
2. Постройте граф игры, в котором
вершины изображают поля. Если из
одного поля ходом коня можно попасть в
другое поле, то соответствующие вершины
следует связать ребром.

9.

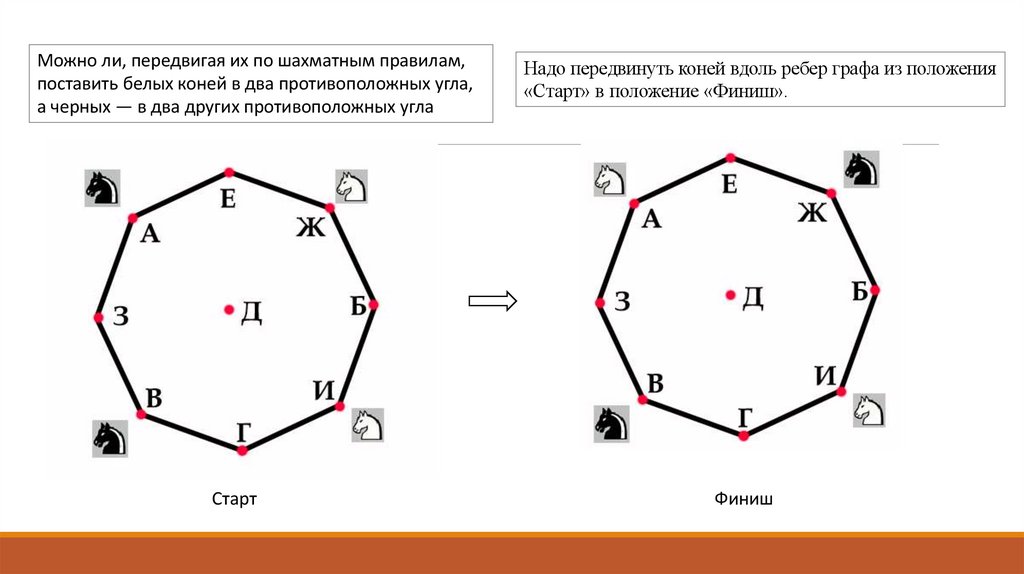
Можно ли, передвигая их по шахматным правилам,
поставить белых коней в два противоположных угла,
а черных — в два других противоположных угла
Старт
Надо передвинуть коней вдоль ребер графа из положения
«Старт» в положение «Финиш».
Финиш

10.

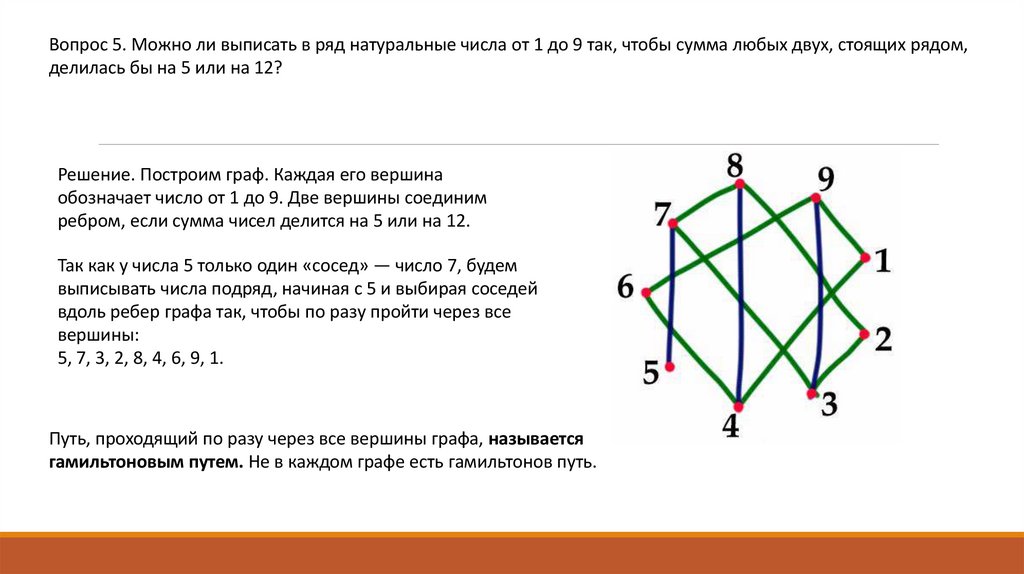
Вопрос 5. Можно ли выписать в ряд натуральные числа от 1 до 9 так, чтобы сумма любых двух, стоящих рядом,
делилась бы на 5 или на 12?
Решение. Построим граф. Каждая его вершина
обозначает число от 1 до 9. Две вершины соединим
ребром, если сумма чисел делится на 5 или на 12.
Так как у числа 5 только один «сосед» — число 7, будем
выписывать числа подряд, начиная с 5 и выбирая соседей
вдоль ребер графа так, чтобы по разу пройти через все
вершины:
5, 7, 3, 2, 8, 4, 6, 9, 1.
Путь, проходящий по разу через все вершины графа, называется
гамильтоновым путем. Не в каждом графе есть гамильтонов путь.

11. Понятия из теории графов

1. Если ребро графа соединяет две его вершины, то говорят, что это
ребро им инцидентно.
2. Две вершины графа называются смежными, если существует
инцидентное им ребро.
q
E
C
D
5. Число ребер, инцидентных некоторой вершине a, называется степенью
этой вершины и обозначается deg(a). Если ребро соединяет вершину с
этой же вершиной (ребро образует петлю), то такое ребро считается
дважды.
Иногда степень вершины называют валентностью.
u
p
t
3. Два ребра называются смежными, если они имеют общую вершину.
4. Если граф имеет ребро, у которого начало и конец совпадают, то это
ребро называется петлей
A
s
r
B
deg(A)= ?
deg(B) = ?
deg(C) = ?
deg(D) = ?
deg(E) = ?
Сколько ребер в графе, суммарная степень вершин которого равна а) 2; б) 4; в) 6?
Нарисуйте соответствующие графы

12. Свойства степеней вершин

n
deg(V ) 2m
1. В любом графе сумма степеней вершин в два раза больше числа рёбер.
i 1
Теорема 1. Сумма степеней вершин графа – чётное число.
i
Доказательство. Сумма степеней вершин вдвое больше числа ребер, потому что у каждого ребра два конца.
Вопрос 1: В некотором графе 5 вершин со степенями 0, 2, 2, 3, 3. Сколько в нем ребер?
Вопрос 2: Не отрывая карандаша от бумаги и не проводя одну линию дважды, можно ли нарисовать такую
фигуру?:
Ответ – «нет». В этом графе 4 вершины, и у всех нечетные
степени — 3, 3, 3 и 5. Если бы нужный маршрут
существовал, у начальной и конечной вершины должны
были бы быть нечетные степени. Но остальные вершины
должны быть четной степени: путь в промежуточную
(граф кенигсбергских мостов)
вершину входит, и потом из нее выходит.
ВЕРШИНА НАЗЫВАЕТСЯ ЧЕТНОЙ
ЧЕТНОЕ(НЕЧЕТНОЕ) ЧИСЛО.
(НЕЧЕТНОЙ),
ЕСЛИ
ЕЕ
СТЕПЕНЬ
–

13. Свойства степеней вершин

2. В любом графе число вершин нечётной степени - чётно.
Задание для исследования:
Во время встречи некоторые участники пожали руки другим.
Докажите, что количество участников, сделавших нечётное
число рукопожатий, чётно (лемма о рукопожатиях).
1. Обменяйтесь рукопожатиями с двумя одноклассниками.
2. Обменяйтесь рукопожатиями с тремя одноклассниками.
Зафиксируйте число сделанных рукопожатий.
3. Постройте граф рукопожатий, в котором каждого
участника встречи обозначьте вершиной, а пожавших друг
другу руки соедините ребром.
1
1
3
1

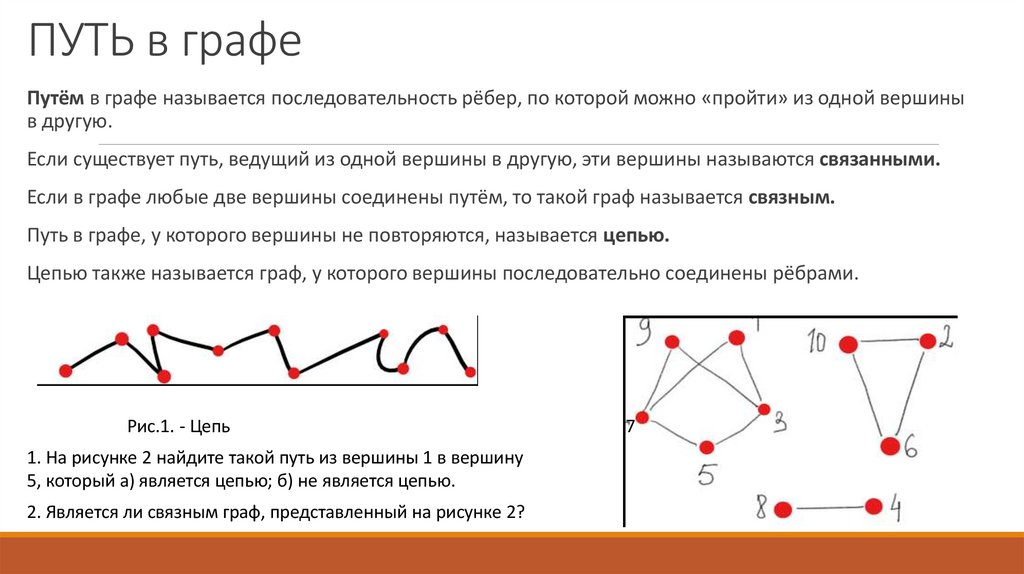
14. ПУТЬ в графе

Путём в графе называется последовательность рёбер, по которой можно «пройти» из одной вершины
в другую.
Если существует путь, ведущий из одной вершины в другую, эти вершины называются связанными.
Если в графе любые две вершины соединены путём, то такой граф называется связным.
Путь в графе, у которого вершины не повторяются, называется цепью.
Цепью также называется граф, у которого вершины последовательно соединены рёбрами.
Рис.1. - Цепь
1. На рисунке 2 найдите такой путь из вершины 1 в вершину
5, который а) является цепью; б) не является цепью.
2. Является ли связным граф, представленный на рисунке 2?
7

15.

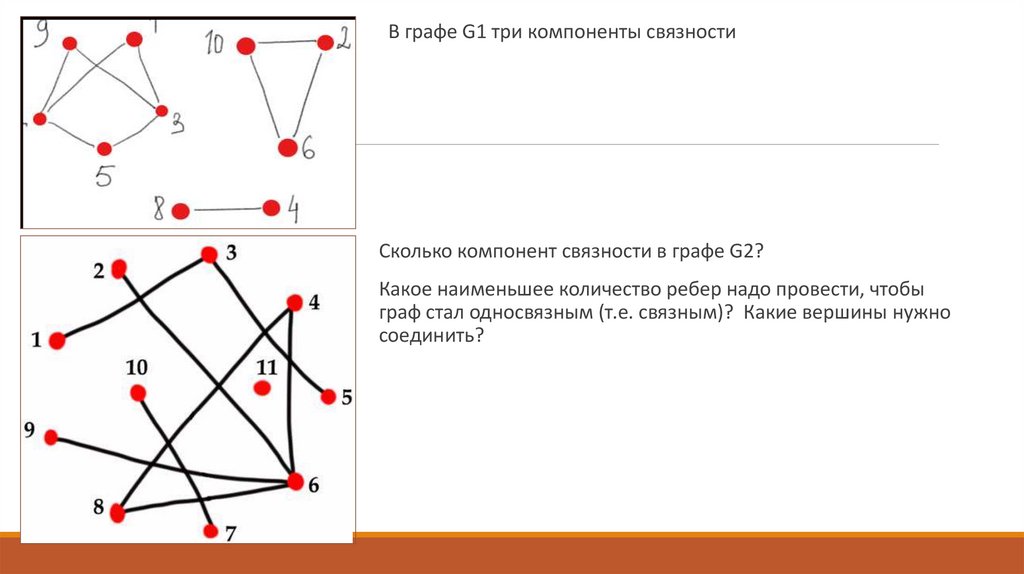
В графе G1 три компоненты связности
Сколько компонент связности в графе G2?
Какое наименьшее количество ребер надо провести, чтобы
граф стал односвязным (т.е. связным)? Какие вершины нужно
соединить?

16.

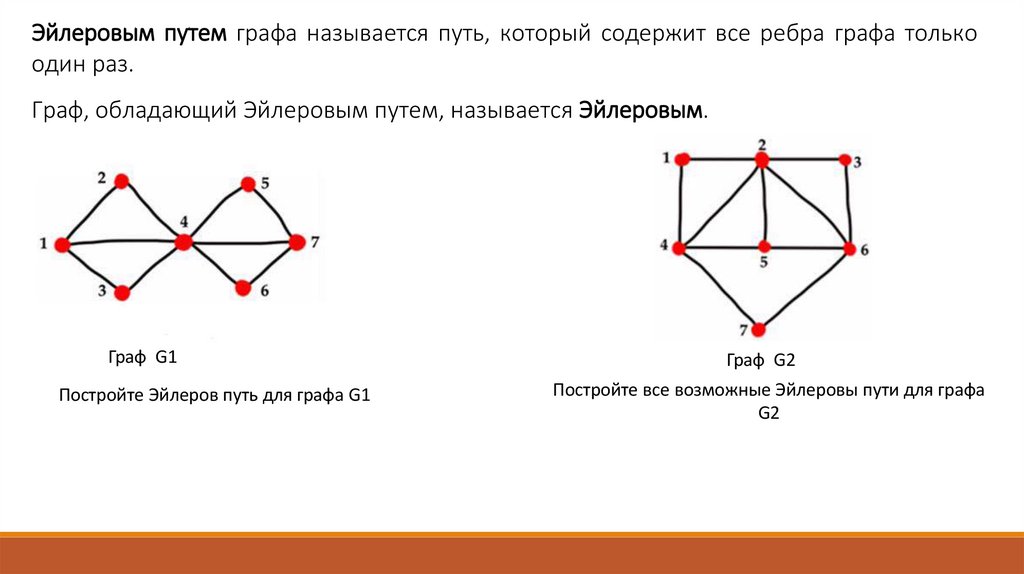
Эйлеровым путем графа называется путь, который содержит все ребра графа только
один раз.
Граф, обладающий Эйлеровым путем, называется Эйлеровым.
Граф G1
Постройте Эйлеров путь для графа G1
Граф G2
Постройте все возможные Эйлеровы пути для графа
G2

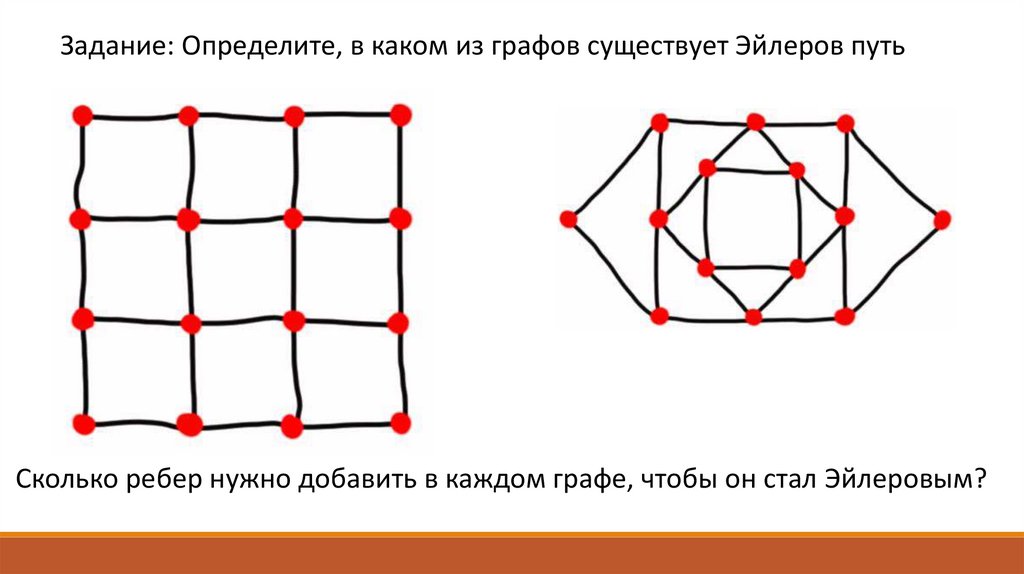
17.

Задание: Определите, в каком из графов существует Эйлеров путь
Сколько ребер нужно добавить в каждом графе, чтобы он стал Эйлеровым?

18. Задания:

1. Авиакомпания «Авиаграф» выполняет полеты между пятью
городами. Столбцы и строки таблицы соответствуют городам. Если в
таблице клетка закрашена, то существует рейс между
соответствующими городами. Нарисуйте граф рейсов этой компании.
Верно ли, что из каждого города можно добраться в каждый (может
быть, с пересадками)?
2. Архипелаг Натуральный состоит из 10 островов, пронумерованных натуральными числами от 1 до 10. Между двумя
островами есть паромная связь, только если сумма их номеров делится на 4. Можно ли с острова 2 перебраться на
остров 8?
3. (Домашнее) Пять листьев кувшинки расположены в вершинах пятиугольника. На трех листьях сидит по лягушке.
Каждая лягушка может прыгнуть по диагонали пятиугольника на свободный лист. Могут ли они прыгать так, чтобы
через некоторое время самая большая лягушка вернулась на исходный лист, а две маленькие лягушки поменялись
местами?
4. Шесть восьмиклассников устроили турнир по настольному теннису; каждый должен сыграть с каждым по одному
разу. Турнир еще не закончился: Мила сыграла 5 партий, Толя — 4 партии, Надя и Даня — по 3 партии, Артем — 2, а
Сеня — 1. С кем играл Артем?
5. (Домашнее) Максим привык что-нибудь рисовать или черкать, разговаривая по телефону.
Вчера он раскрасил в тетради некоторые клетки, причем у каждой раскрашенной клетки
есть одна или три раскрашенных соседки (см. рис.). Мог ли Максим раскрасить 11 клеток?
Максим считает соседними клетками те, у которых есть общая сторона.

19.

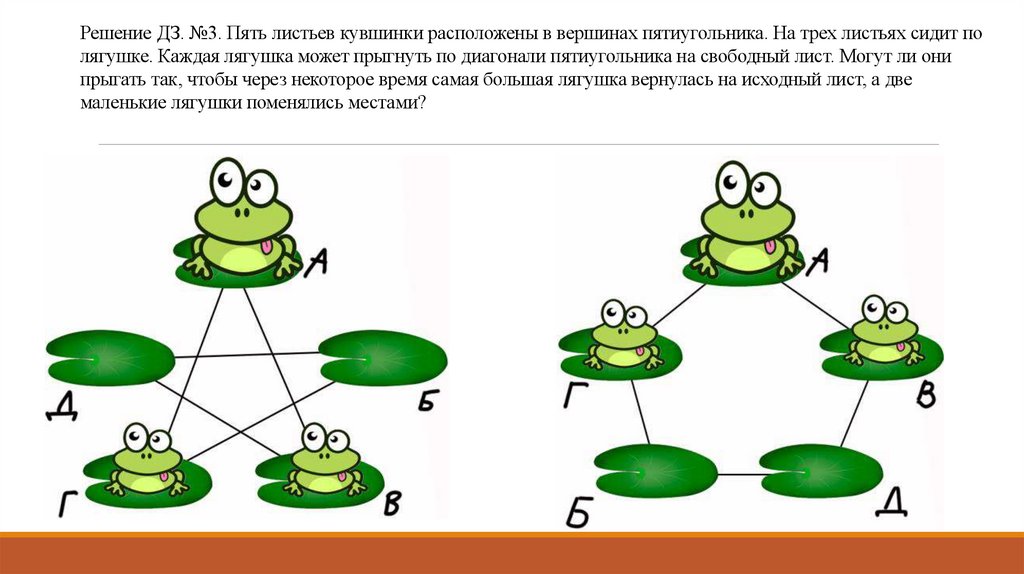
Решение ДЗ. №3. Пять листьев кувшинки расположены в вершинах пятиугольника. На трех листьях сидит по
лягушке. Каждая лягушка может прыгнуть по диагонали пятиугольника на свободный лист. Могут ли они
прыгать так, чтобы через некоторое время самая большая лягушка вернулась на исходный лист, а две
маленькие лягушки поменялись местами?

20.

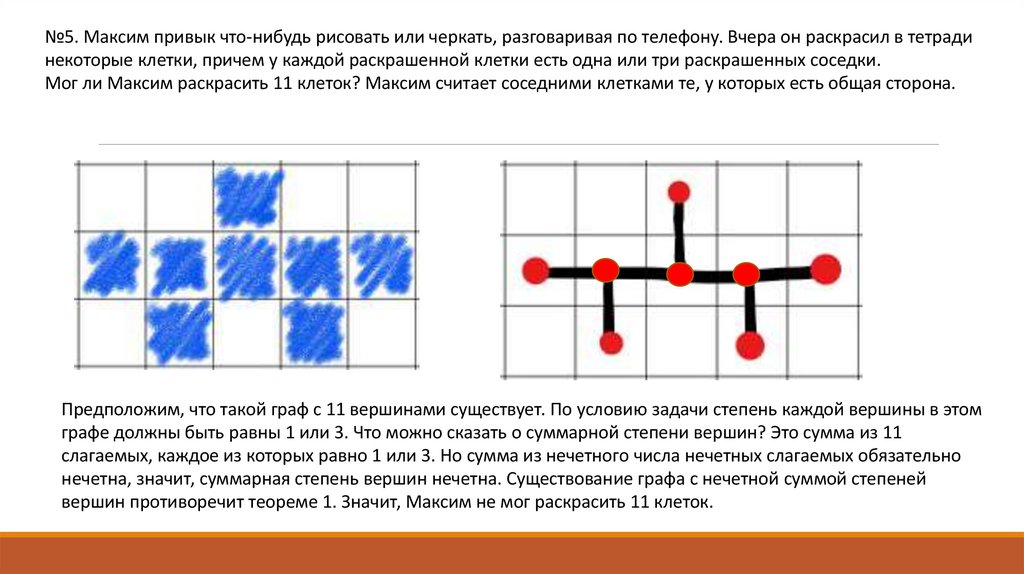
№5. Максим привык что-нибудь рисовать или черкать, разговаривая по телефону. Вчера он раскрасил в тетради
некоторые клетки, причем у каждой раскрашенной клетки есть одна или три раскрашенных соседки.
Мог ли Максим раскрасить 11 клеток? Максим считает соседними клетками те, у которых есть общая сторона.
Предположим, что такой граф с 11 вершинами существует. По условию задачи степень каждой вершины в этом
графе должны быть равны 1 или 3. Что можно сказать о суммарной степени вершин? Это сумма из 11
слагаемых, каждое из которых равно 1 или 3. Но сумма из нечетного числа нечетных слагаемых обязательно
нечетна, значит, суммарная степень вершин нечетна. Существование графа с нечетной суммой степеней
вершин противоречит теореме 1. Значит, Максим не мог раскрасить 11 клеток.

21. Циклы. Деревья. Дерево случайного эксперимента.

22.

Почтальон разносит почту. Он должен обойти все улицы и вернуться на почту.
Со склада сетевого магазина требуется развести товары во все магазины сети и
вернуться в исходную точку.
Такие пути в графе называются циклами (греч. Κύκλος - «круг», «окружность»)
Пройдя по циклу, мы замыкаем путешествие, возвращаясь в исходную точку.
Определение. Путь в графе, у которого первая и последняя вершины совпадают, а
промежуточные вершины не повторяются, называется циклом.

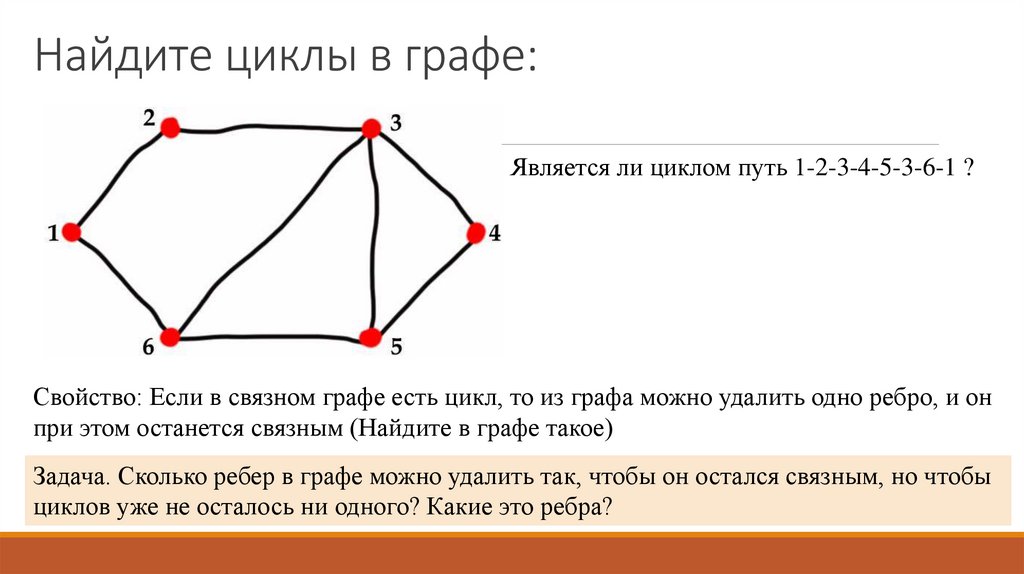
23. Найдите циклы в графе:

Является ли циклом путь 1-2-3-4-5-3-6-1 ?
Свойство: Если в связном графе есть цикл, то из графа можно удалить одно ребро, и он
при этом останется связным (Найдите в графе такое)
Задача. Сколько ребер в графе можно удалить так, чтобы он остался связным, но чтобы
циклов уже не осталось ни одного? Какие это ребра?

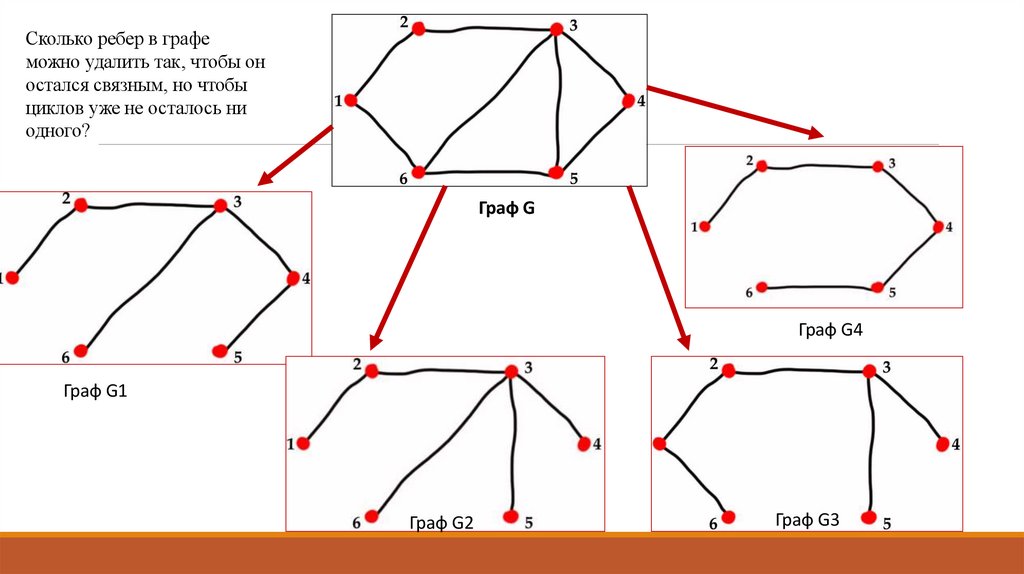
24.

Сколько ребер в графе
можно удалить так, чтобы он
остался связным, но чтобы
циклов уже не осталось ни
одного?
Граф G
Граф G4
Граф G1
Граф G2
Граф G3

25.

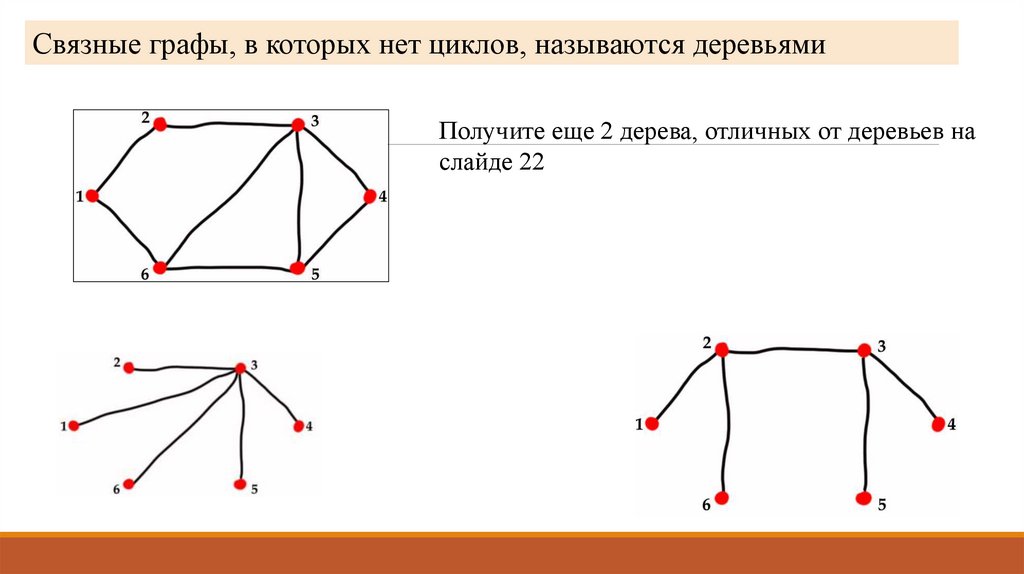
Связные графы, в которых нет циклов, называются деревьями
Получите еще 2 дерева, отличных от деревьев на
слайде 22

26. Свойства деревьев

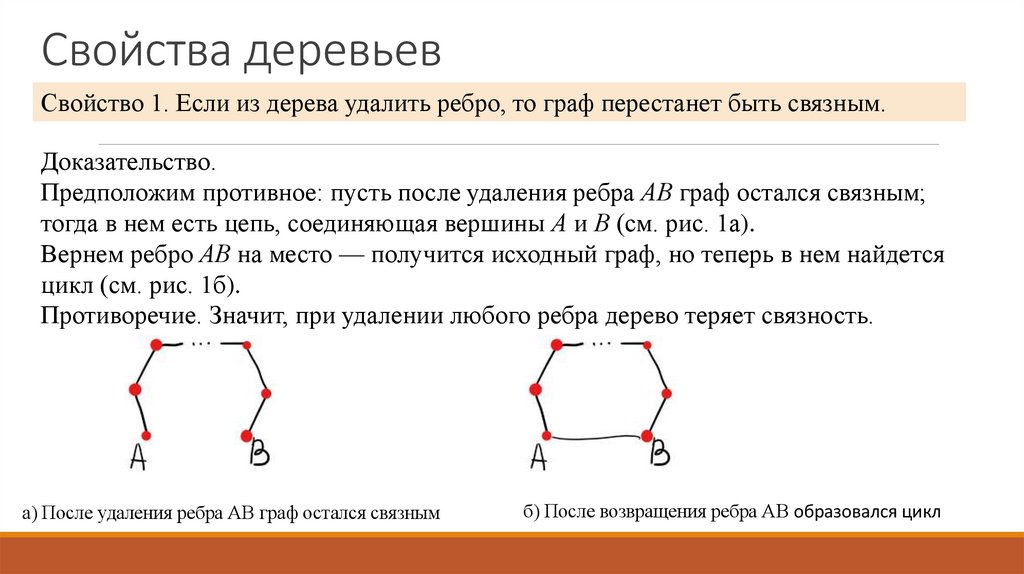
Свойство 1. Если из дерева удалить ребро, то граф перестанет быть связным.
Доказательство.
Предположим противное: пусть после удаления ребра АВ граф остался связным;
тогда в нем есть цепь, соединяющая вершины А и В (см. рис. 1а).
Вернем ребро АВ на место — получится исходный граф, но теперь в нем найдется
цикл (см. рис. 1б).
Противоречие. Значит, при удалении любого ребра дерево теряет связность.
а) После удаления ребра АВ граф остался связным
б) После возвращения ребра АВ образовался цикл

27.

Концевой (или висячей) вершиной называется вершина, из которой выходит
ровно одно ребро, то есть вершина степени 1.
Свойство 2. Если дерево конечно (в нем конечное число вершин) и есть хотя бы
одно ребро, то в таком дереве есть концевая вершина.
! Придумайте дерево без концевых вершин.
Свойство 3. В конечном дереве число ребер на 1 меньше числа вершин.
Доказательство. Если ребер нет, то дерево состоит из единственной вершины. Значит, в этом дереве
вершин на 1 больше, чем ребер: 1-0=1
Пусть теперь в графе n ребер (n>0 ). Мы знаем, что в таком дереве есть концевая вершина. Удалим ее
вместе со входящим в нее ребром. Снова получится дерево. Будем удалять концевые вершины вместе со
входящими в них ребрами до тех пор, пока не останется одна-единственная вершина.
Мы удалили все n ребер и висящие на них n концевых вершин. Осталась одна вершина и не осталось ни
одного ребра. Следовательно, в исходном дереве было n+1 вершин и n ребер. То есть, вершин на одну
больше.

28.

Дерево случайного эксперимента
Задача. Трое друзей Вася, Петя и Слава купили торт, и решили его съесть. Они разделили торт на
три равных части. Внезапно появился четвертый друг Коля, и друзья решили отрезать ему по
кусочку от своей доли. Вася отрезал 1/3 от своего куска, Петя 1/4, а Слава – половину. Какую часть
всего торта получил в итоге Коля?
1. Сначала торт разрезали на три равные части, и
каждому из трех друзей досталось по 1/3 торта.
2. Затем пришел Коля и каждый мальчик отрезал ему
соответствующую часть своего куска:
3. В итоге Коля получит
1 1 1 1 1 1
* * * ?
3 3 3 4 3 2

29. Дерево случайного эксперимента

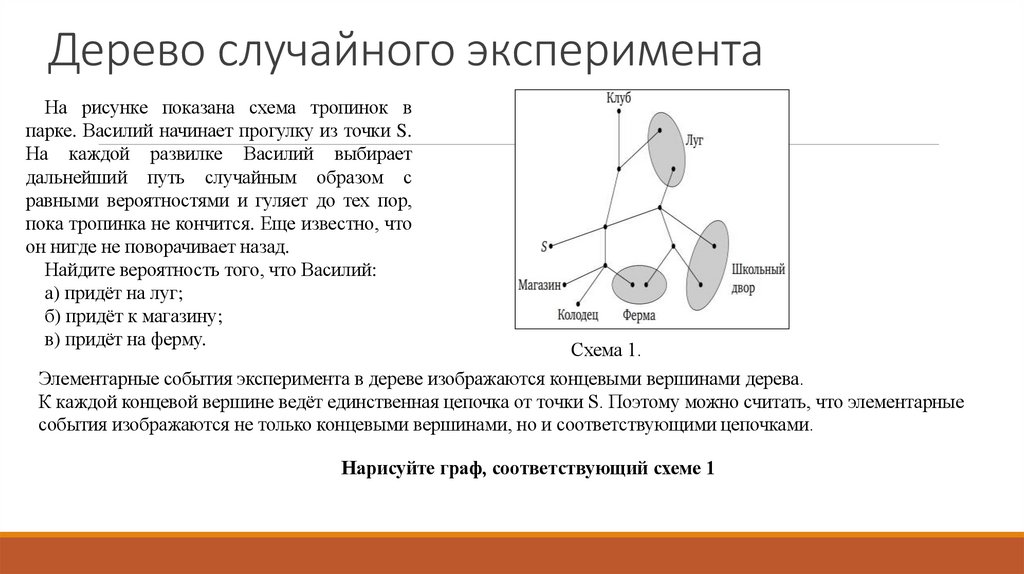
На рисунке показана схема тропинок в
парке. Василий начинает прогулку из точки S.
На каждой развилке Василий выбирает
дальнейший путь случайным образом с
равными вероятностями и гуляет до тех пор,
пока тропинка не кончится. Еще известно, что
он нигде не поворачивает назад.
Найдите вероятность того, что Василий:
а) придёт на луг;
б) придёт к магазину;
в) придёт на ферму.
Схема 1.
Элементарные события эксперимента в дереве изображаются концевыми вершинами дерева.
К каждой концевой вершине ведёт единственная цепочка от точки S. Поэтому можно считать, что элементарные
события изображаются не только концевыми вершинами, но и соответствующими цепочками.
Нарисуйте граф, соответствующий схеме 1

30. Дерево случайного эксперимента

Случайные эксперименты и случайные события.
Дискретные и непрерывные множества элементарных
событий

31. Случайные эксперименты и случайные события. Дискретные и непрерывные множества элементарных событий

Что такое случайное событие?
Теория вероятностей рассматривает случайные события не сами по себе, а в рамках случайных опытов
(случайных экспериментов).
Случайный эксперимент — это условия и обстоятельства, в рамках которых рассматриваются
случайные события.
Само слово «эксперимент» обычно означает сознательные действия какого-то лица.
В теории вероятности слово «эксперимент» употребляется в широком смысле, даже когда речь идёт о
случайных процессах в природе или обществе.
Примеры случайных экспериментов, проводимых
человеком:
––
выбор
объекта
для
обследования
в
социологических,
медицинских
и
других
исследованиях или при контроле качества
продукции;
–– измерение какой-либо величины, например,
срока жизни изделия, или расстояния, которое
сможет проехать автомобиль на десяти литрах
бензина;
–– бросание жребия, например, игральной кости
или монеты;
Примеры природных и социальных случайных явлений
(в терминологии ТВ – экспериментов), в которых велика
доля случая:
–– формирование погоды в определённое время в
определённом месте;
–– землетрясения, извержения вулканов, лесные пожары
или наводнения;
–– социальные или экономические процессы: рождаемость
и смертность, занятость населения, показатели инфляции,
цен и т. д.

32. Что такое случайное событие?

О случайных событиях можно говорить только при определённых условиях. Если таких условий нет, то нет и
наступления событий. Например, случайное событие «появление орла» возможно только в эксперименте с
подбрасыванием монеты. Без этого действия о выпадении орла нельзя говорить.
Условия и действия, при которых может осуществиться случайное событие,
принято называть случайным опытом или случайным экспериментом.
Случайный опыт (эксперимент, наблюдение, испытание) - это некоторое действие, которое можно
повторить большое количество раз в одинаковых условиях, а результат этого действия зависит от
случая и его невозможно предсказать.
Пример. О случайном событии «электрическая лампочка прослужит более 100 часов» можно
говорить, только если имеется лампочка, которую включают в электрическую сеть. Тогда
случайный эксперимент заключается в наблюдении за горящей лампочкой.
Результатом случайного опыта является случайное элементарное событие
Случайное событие - это событие, которое в ходе опыта может произойти или не произойти.
При бросании одной монеты возможно всего
два элементарных события: «орёл» и «решка»
{О, Р} – множество элементарных событий
При бросании двух монет элементарных исходов четыре.
Множество элементарных событий этого эксперимента:
{ОО, ОР, РО, РР}

33.

ТИПЫ элементарных событий
Дискретное множество элементарных
событий (оно конечно или счётно).
Множество элементарных событий
непрерывно.
Множество элементарных событий счётно, если
все элементарные события можно пронумеровать
натуральными числами.
Элементарное событие описывается точкой на
числовой прямой или отрезке (время безотказной
работы лампочки, температура воздуха, расстояние
между точками, масса тела).
? Какое множество элементарных событий ––
дискретное или непрерывное –– возникает в
экспериментах:
Измерение температуры воздуха
Подсчет голосов избирателей, проголосовавших за
определённого кандидата?

34.

Определение. Случайным событием называют произвольное
подмножество множества элементарных событий.
Говорят, что в случайном эксперименте происходит случайное событие A, если эксперимент заканчивается одним
из элементарных событий, принадлежащих (благоприятствующих) событию A.
События принято обозначать прописными (большими) латинскими буквами.
Пример. Правильную игральную кость бросают один раз.
Даны события:
а)M = {выпало не больше, чем 3 очка}
б)N = {выпало чётное число очков}
Элементарные исходы событий:
M ={1, 2, 3}; N = {2,4,6}
Задание 1. Случайный опыт заключается в двукратном
бросании монеты.
Запишите, из каких элементарных событий состоит
событие:
а) А = {выпала хотя бы одна решка};
б) В= {оба раза монета выпала одной и той же стороной};
в) С ={ оба раза выпала решка}
Задание 2. Опыт «стрельба по мишени до первого
попадания». Обозначим попадание П, а промах Н.
Тогда элементарные события –– последовательности букв Н
и П: П, НП, ННП и т. д.
Запишите, из каких элементарных событий состоит
событие:
А={потребуется не более 5 выстрелов, чтобы поразить
мишень}.

35.

В результате проводимого случайного опыта какие-то события могут произойти наверняка, а какие-то
точно не состоятся.
Достоверное событие это событие, которое наверняка произойдёт в проводимом случайном опыте.
Невозможное событие это событие, которое никогда не произойдёт в проводимом случайном
опыте.
Например, если в урне все шары черные, то вытащить чёрный шар является достоверным событием,
а достать белый шар является невозможным событием.
Теория вероятностей это раздел математики, изучающий случайные события, случайные величины,
их свойства и операции над ними.
При подбрасывании монеты выпала решка. Является ли данное событие случайным?
Укажите, какие из перечисленных событий являются достоверными, а какие невозможными:
на игральном кубике выпало от одного до шести очков;
номер открытой страницы в книге дробное число;
после весны наступает лето.

36.

Два события, которые в данных условиях могут происходить одновременно,
называются совместными, а те, которые не могут происходить
одновременно, - несовместными.
Равновозможными называются события, когда в их наступлении нет
преимуществ.
Неравновозможные события те, у которых в наступлении одного из
событий есть какое то преимущество.

37.

Классическое определение вероятности
Вероятностью события А при проведении некоторого испытания
называют отношение числа тех исходов, в результате которых наступает
событие А, к общему числу всех (равновозможных между собой) исходов
этого испытания.
Алгоритм вычисления вероятности
случайного события
Для нахождения вероятности случайного события А при проведении некоторого
испытания следует найти:
1) число N всех возможных исходов данного испытания;
2) количество N(A) тех исходов, в которых наступает событие А;
3) частное Р(А) = N ( A) является вероятностью события А.
N

38.

Решение.
Пример 1.
Число стандартных подшипников
На завод привезли партию из 1000 подшипников. Случайно
равно 1000 – 30 = 970.
в эту партию попало 30 подшипников, не удовлетворяющих
Считаем, что каждый подшипник
стандарту. Определить вероятность Р(А) того, что взятый
наудачу подшипник окажется стандартным.
имеет одинаковую вероятность быть
выбранным.
Тогда полная группа событий состоит
из
N = 1000 равновероятных исходов, из
которых событию А благоприятствуют
N(A) = 970 исходов.
Поэтому P=970/1000
Ответ: 0,97.

39.

Пример 2
Найти вероятность того, что при одном бросании игральной
кости (кубика) выпадает:
А) три очка
Б) число очков, кратное трем;
В) Число очков больше трех;
Г) число очков, не кратное трем

40.

События А и В называются противоположными,
если всякое наступление события А означает ненаступление события В, а
ненаступление события А – наступление события В.
Событие, противоположное событию А, обозначают
символом Ᾱ. Сумма вероятностей противоположных событий равна 1.
P(A)+P(Ᾱ)=1.
Пример: Бросаем один раз игральную кость. Событие А –
выпадение четного числа очков, тогда событие Ā - выпадение
нечетного числа очков.

41.

Задания.
1. В среднем из 1000 аккумуляторов, поступивших в продажу, 6
неисправны. Найдите вероятность того, что один купленный
аккумулятор окажется исправным.
2. Игральная кость бросается два раза. Какова вероятность того,
что сумма выпавших очков равна 6 ?

42.

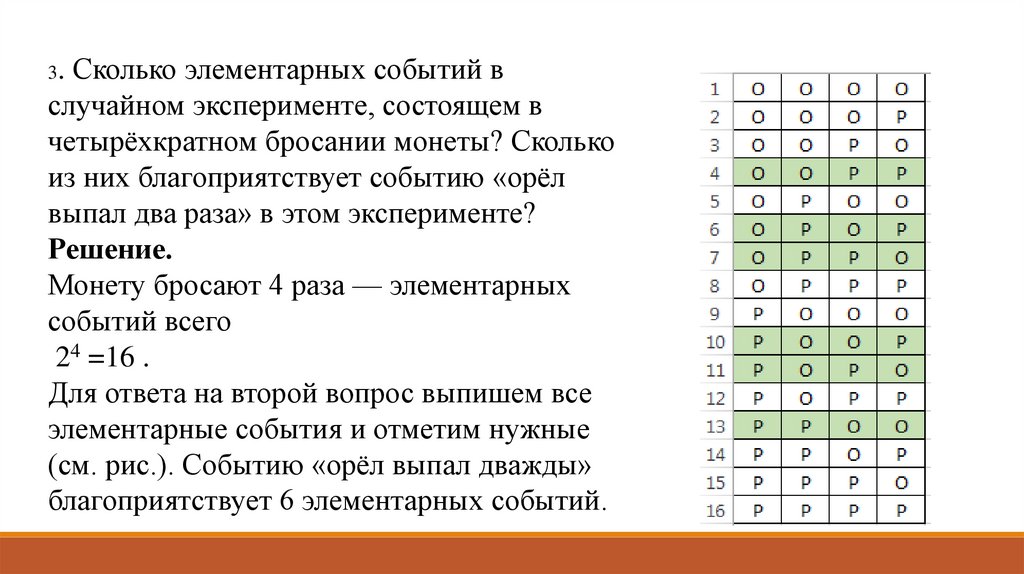
3. Сколько элементарных событий в
случайном эксперименте, состоящем в
четырёхкратном бросании монеты? Сколько
из них благоприятствует событию «орёл
выпал два раза» в этом эксперименте?
Решение.
Монету бросают 4 раза — элементарных
событий всего
24 =16 .
Для ответа на второй вопрос выпишем все
элементарные события и отметим нужные
(см. рис.). Событию «орёл выпал дважды»
благоприятствует 6 элементарных событий.

43.

Задания
1. Рассмотрим опыт «стрельба по мишени до первого попадания».
Событие
A = {мишень поражена первым или вторым выстрелом}
можно записать перечислением элементарных событий:
A = {П, НП}.
Здесь буква Н обозначает промах, а буква П –– попадание.
Запишите перечислением элементарных событий следующие события:
а) B= {потребуется не более трёх выстрелов, чтобы поразить мишень}
б) C= {потребуется от двух до пяти выстрелов, чтобы поразить мишень}
в) D= {потребуется не менее трёх выстрелов, чтобы поразить мишень}
3. Игральную кость бросают дважды. Если при первом броске выпало
a очков, а при втором –– b очков, то элементарное событие записывают
(a; b).
Перечислите все элементарные события, составляющие событие:
а) A={выпавшие числа отличаются на 2};
б) B={сумма очков не меньше 10}.
2. К условию задания 1
сформулировать словами события:
а) E ={НП, ННП, НННП};
б) F ={П, ННП};
в) G={НННП, ННННП, НННННП, ...}.
4. Эксперимент состоит в случайном
выборе двух цветных карточек из
четырёх имеющихся: красной (К),
синей (С), зелёной (З) и жёлтой (Ж).
При этом порядок выбора не важен.
А) Запишите перечислением
элементарных событий событие
B = {зелёная карточка не выбрана}.
Б) Является ли событием этого опыта
событие
C = {Ж, СЖК}?