Similar presentations:
26.01
1. нормальное распределение
26.01НОРМАЛЬНОЕ
РАСПРЕДЕЛЕНИЕ
Понятие о нормальном распределении и его свойства
2. Особый тип распределения, при котором большинство значений сосредоточено около среднего, называется нормальным распределением.
Нормальное распределениечасто называют распределением Гаусса.
Карл Гаусс – выдающийся немецкий
математик, физик, механик, астроном,
геодезист. Его считали одним из величайших
математиков всех времен. В 1838 году
награжден медалью Копли.
«Математика – царица наука, арифметика –
царица математики» – любимое выражение
великого математика Карла Гаусса. «Король
математики» работал над доказательством
ряда алгебраических и геометрических
теорем.
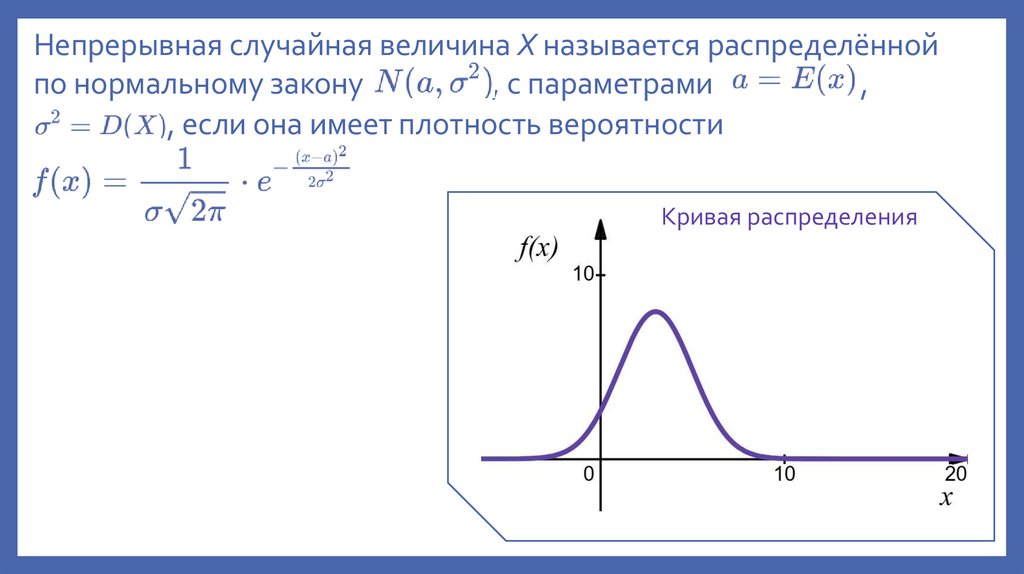
3. Непрерывная случайная величина X называется распределённой по нормальному закону , с параметрами ,
, если она имеет плотность вероятностиКривая распределения
4.
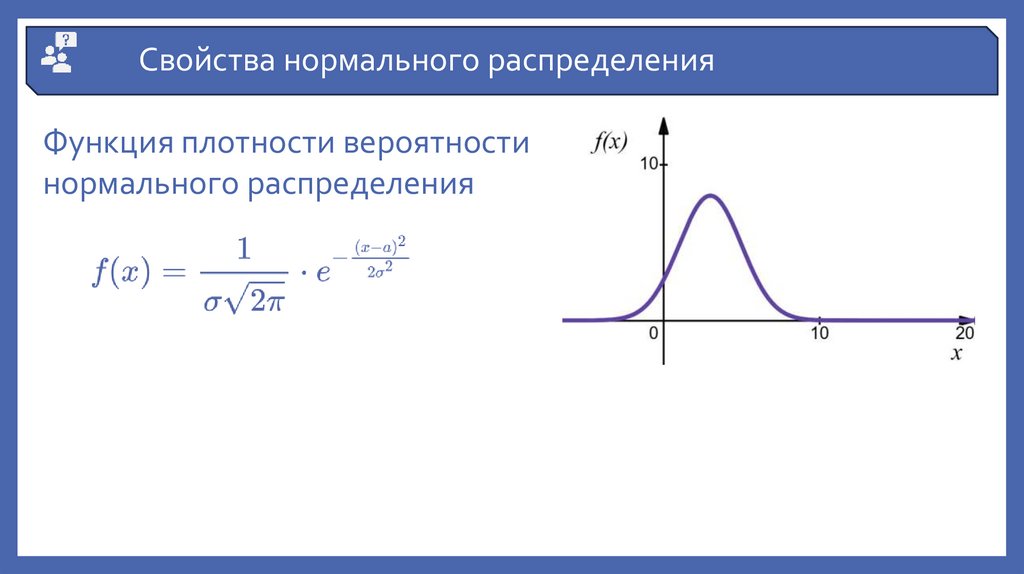
Свойства нормального распределенияФункция плотности вероятности
нормального распределения
5.
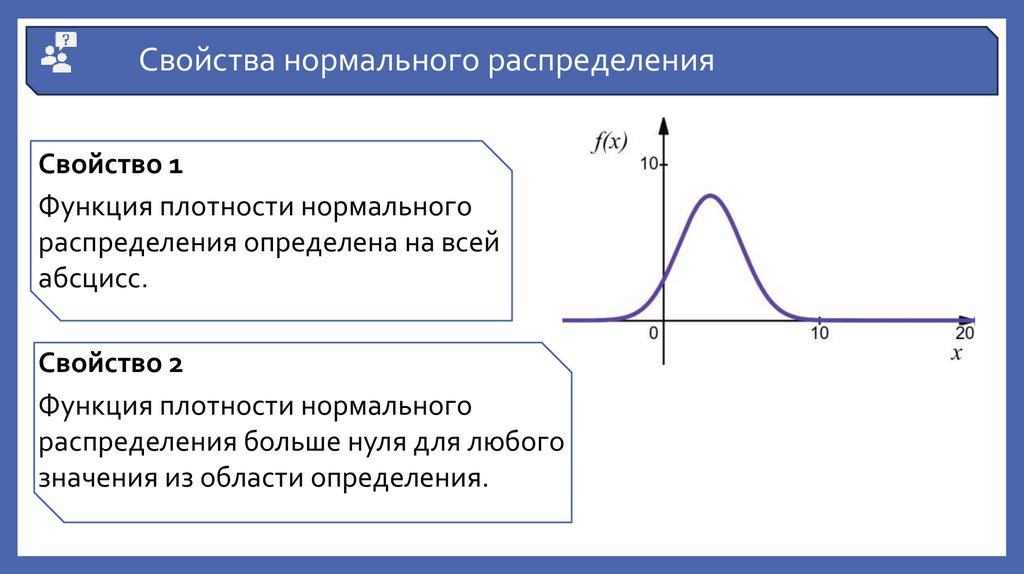
Свойства нормального распределенияСвойство 1
Функция плотности нормального
распределения определена на всей
абсцисс.
Свойство 2
Функция плотности нормального
распределения больше нуля для любого
значения из области определения.
6.
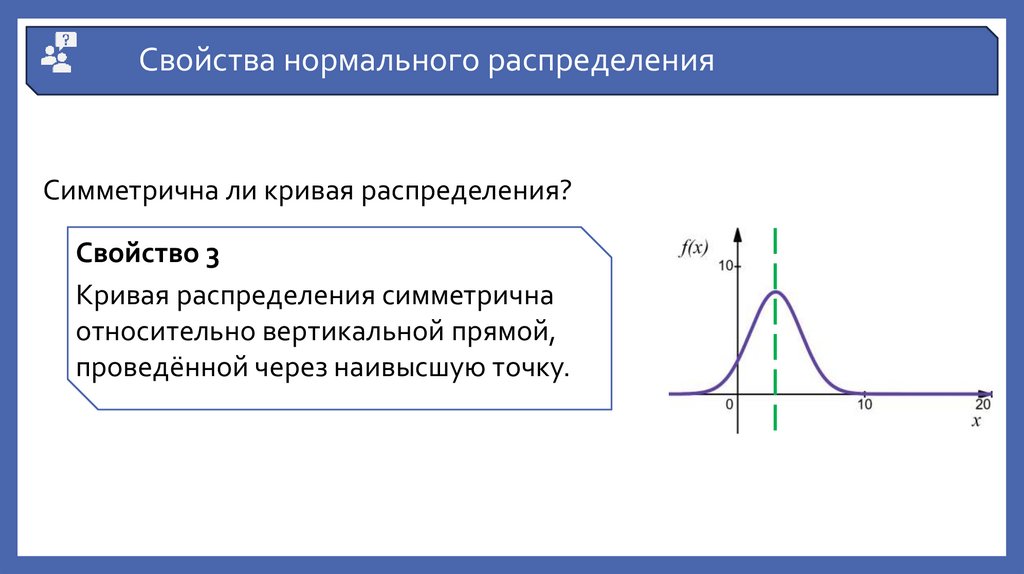
Свойства нормального распределенияСимметрична ли кривая распределения?
Свойство 3
Кривая распределения симметрична
относительно вертикальной прямой,
проведённой через наивысшую точку.
7.
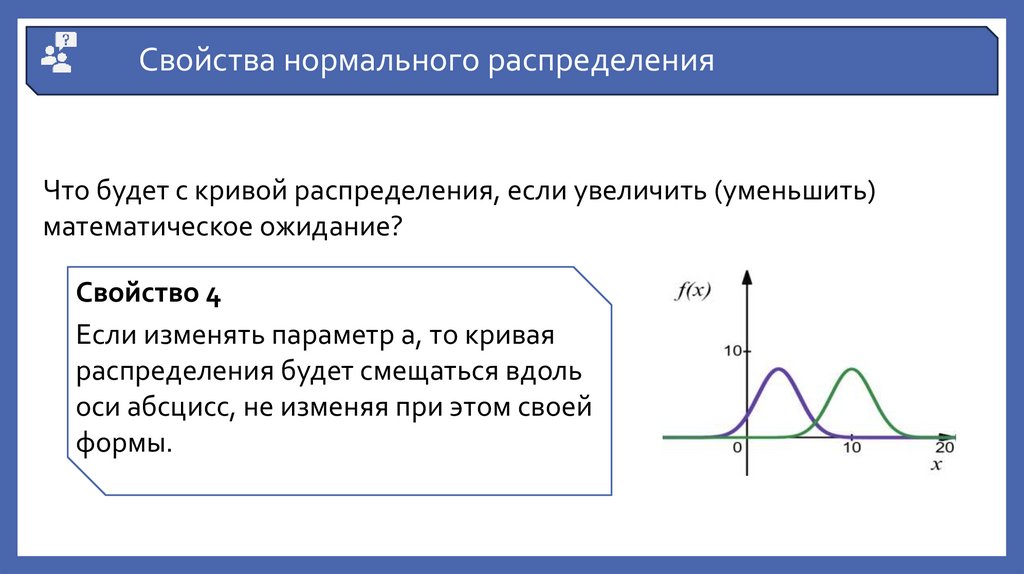
Свойства нормального распределенияЧто будет с кривой распределения, если увеличить (уменьшить)
математическое ожидание?
Свойство 4
Если изменять параметр а, то кривая
распределения будет смещаться вдоль
оси абсцисс, не изменяя при этом своей
формы.
8.
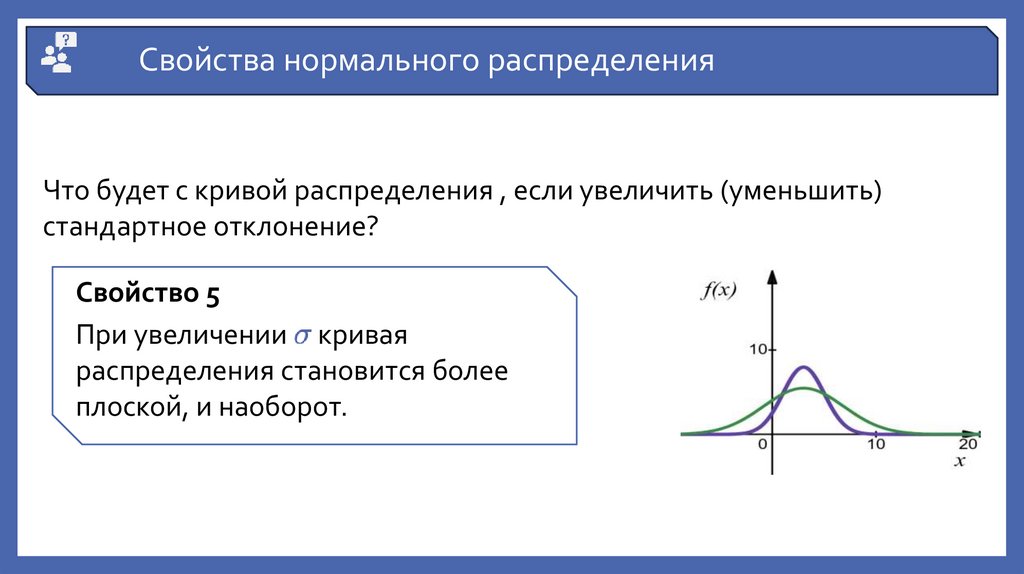
Свойства нормального распределенияЧто будет с кривой распределения , если увеличить (уменьшить)
стандартное отклонение?
Свойство 5
При увеличении кривая
распределения становится более
плоской, и наоборот.
9.
ЗадачаМонетка подбрасывается 10 раз. Какова вероятность того, что точно
6 раз выпадет орёл?
Сколькими способами можно «выбрать» 6 орлов из 10 бросков?
Сколько всего будет исходов?
10.
Монетка подбрасывается 10 раз. Какова вероятность того, что точно6 раз выпадет орёл?
Сколькими способами можно «выбрать» 6 орлов из 10 бросков?
Сколько всего будет исходов?
Решение
− количество способов,
которыми можно
«выбрать» 6 орлов из 10
бросков.
− всего исходов.
11.
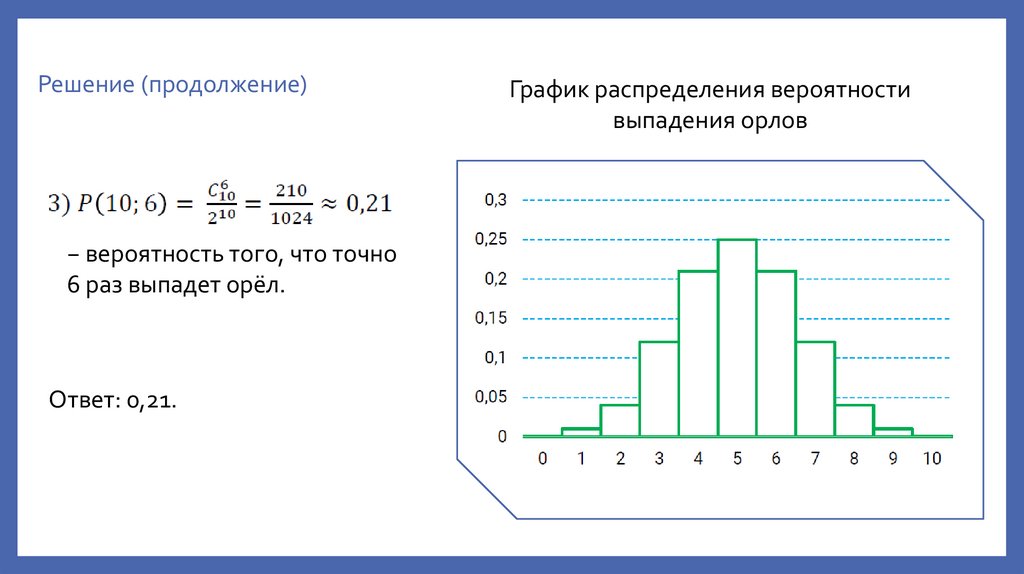
Решение (продолжение)− вероятность того, что точно
6 раз выпадет орёл.
Ответ: 0,21.
График распределения вероятности
выпадения орлов
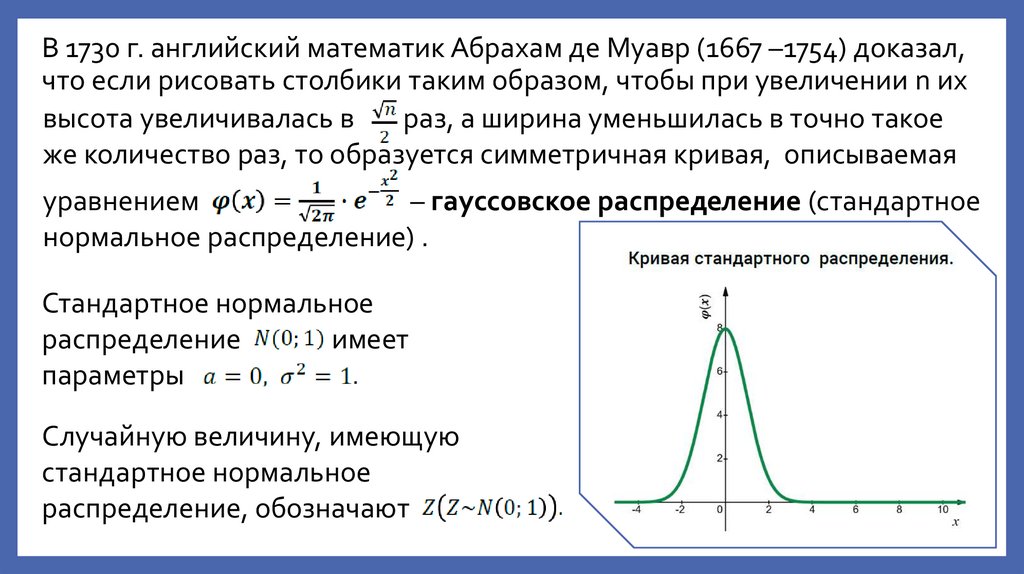
12. В 1730 г. английский математик Абрахам де Муавр (1667 –1754) доказал, что если рисовать столбики таким образом, чтобы при
увеличении n ихвысота увеличивалась в
раз, а ширина уменьшилась в точно такое
же количество раз, то образуется симметричная кривая, описываемая
уравнением
– гауссовское распределение (стандартное
нормальное распределение) .
σ — стандартное отклонение
σ² — дисперсия
e — основание натурального логарифма (≈ 2,71828)
π — число пи (≈ 3,14159)
13. В 1730 г. английский математик Абрахам де Муавр (1667 –1754) доказал, что если рисовать столбики таким образом, чтобы при
увеличении n ихвысота увеличивалась в
раз, а ширина уменьшилась в точно такое
же количество раз, то образуется симметричная кривая, описываемая
уравнением
– гауссовское распределение (стандартное
нормальное распределение) .
Стандартное нормальное
распределение
имеет
параметры
Случайную величину, имеющую
стандартное нормальное
распределение, обозначают
14.
Задание 1Плотность вероятности нормально распределённой случайной
величина Х имеет вид:
Определите:
1. коэффициент С;
2. дисперсию .
Решение
1. Плотность распределения нормальной случайной
величины
Получаем, a = 2.
.
2.
Ответ:
,
.
,
,
.
15.
Задание 2Напишите функцию плотности нормального распределения
случайной величины Х, если известно, что математическое ожидание
равно 2, а
Решение
Плотность распределения нормальной случайной
величины
Ответ:
16.
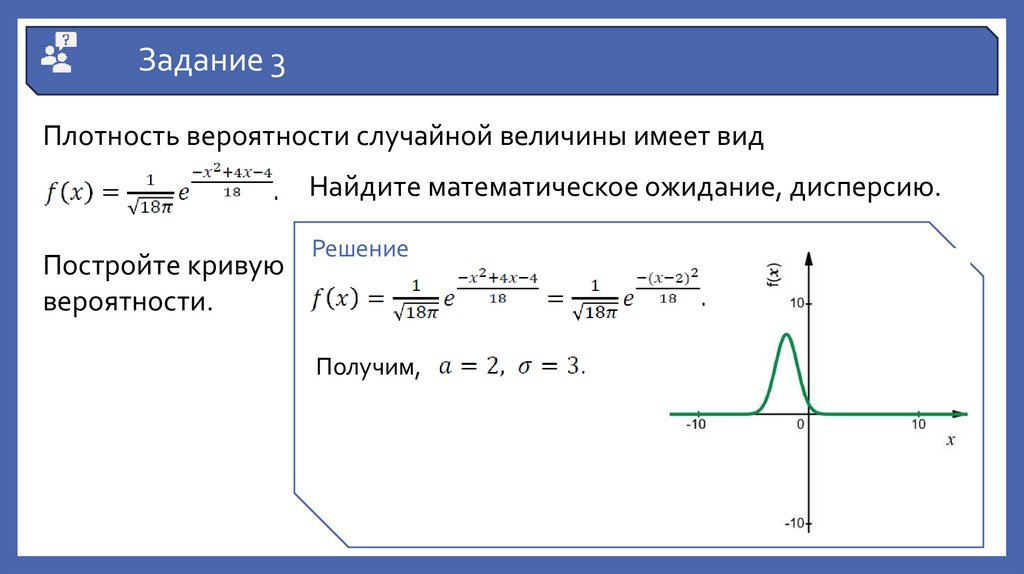
Задание 3Плотность вероятности случайной величины имеет вид
Найдите математическое ожидание, дисперсию.
Постройте кривую
вероятности.
Решение
Получим,
17.
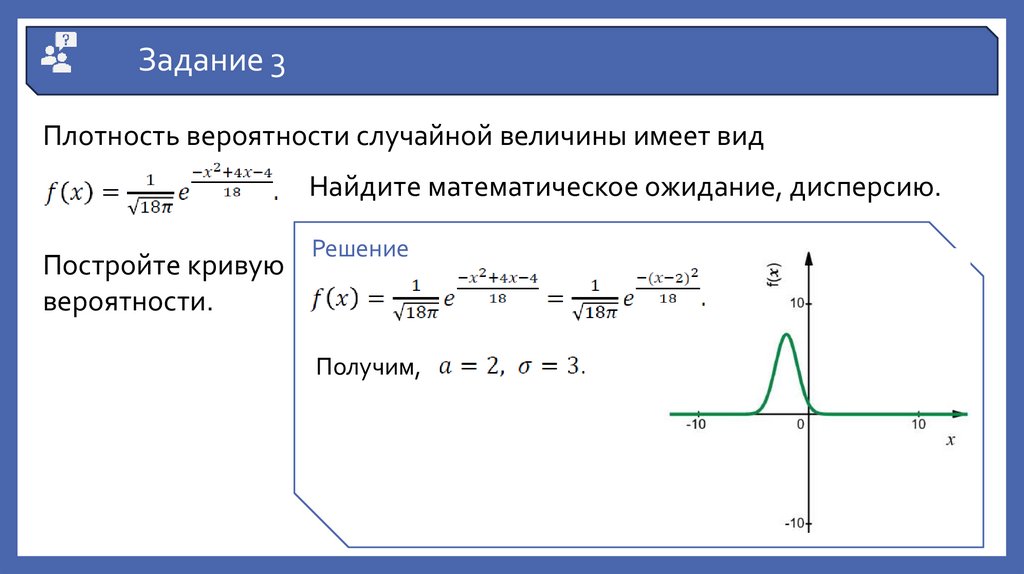
Задание 3Плотность вероятности случайной величины имеет вид
Найдите математическое ожидание, дисперсию.
Постройте кривую
вероятности.
Решение
Получим,
18.
Домашнее заданиеЗаконспектировать, записать и разобрать примеры заданий