Методы_решения_уравнений_и_неравенств

1.

Методы решения
уравнений
Математические уравнения и неравенства являются основой для
моделирования реальных процессов в науке и технике. Понимание
различных методов их решения позволяет эффективно
анализировать и прогнозировать поведение систем. В данной
презентации рассматриваются основные типы уравнений и
неравенств, а также методы их решения, что необходимо для
успешного освоения прикладных дисциплин в техникуме.

2.

Линейные уравнения
Общий вид
Пример
Неравенства
Линейное уравнение имеет вид
ax + b = 0, где коэффициент 'a'
не равен нулю. Для нахождения
неизвестной 'x' необходимо
разделить 'b' на 'a' с
противоположным знаком: x = b/a.
Рассмотрим уравнение 2x + 4 =
0. Переносим 4 в правую часть:
2x = -4. Делим обе части на 2: x
= -2.
Линейные неравенства вида ax
+ b > 0 решаются аналогично,
но при делении на
отрицательный коэффициент 'a'
знак неравенства меняется на
противоположный.

3.

Квадратные уравнения
Общий вид
Нахождение корней
Квадратное уравнение имеет вид ax² + bx + c = 0, где
коэффициент 'a' не равен нулю. Для его решения
используется формула дискриминанта D = b² - 4ac.
Корни квадратного уравнения вычисляются по формуле
x₁,₂ = (-b ± √D) / 2a, где √D — квадратный корень из
дискриминанта.
Количество корней
Если D > 0, уравнение имеет два различных
действительных корня. При D = 0 существует один
действительный корень, а если D < 0, действительных
корней нет.

4.

Рациональные уравнения и неравенства
1
2
3
Уравнения
Рациональные уравнения вида P(x)/Q(x) = 0 решаются приравниванием числителя к нулю: P(x) = 0, при условии, что
знаменатель Q(x) не равен нулю.
Пример
Для уравнения (x² - 4) / (x - 2) = 0, решаем x² - 4 = 0, что дает x = 2 или x = -2. Поскольку x ≠ 2, единственным решением
является x = -2.
Неравенства
Решение рациональных неравенств P(x)/Q(x) > 0 выполняется с использованием метода интервалов, который
учитывает знаки числителя и знаменателя на числовой оси.

5.

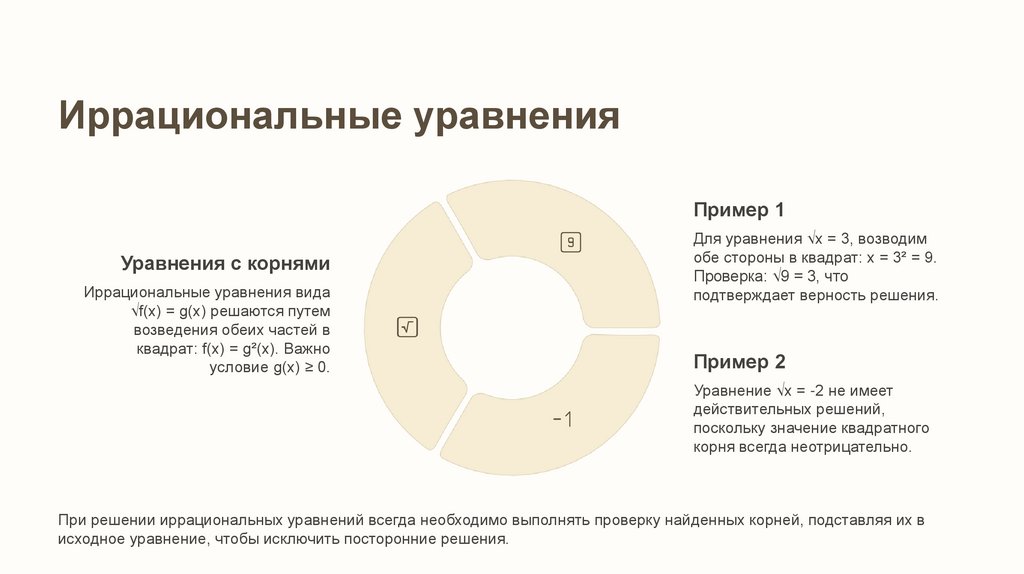
Иррациональные уравнения
Пример 1
Уравнения с корнями
Иррациональные уравнения вида
√f(x) = g(x) решаются путем
возведения обеих частей в
квадрат: f(x) = g²(x). Важно
условие g(x) ≥ 0.
Для уравнения √x = 3, возводим
обе стороны в квадрат: x = 3² = 9.
Проверка: √9 = 3, что
подтверждает верность решения.
Пример 2
Уравнение √x = -2 не имеет
действительных решений,
поскольку значение квадратного
корня всегда неотрицательно.
При решении иррациональных уравнений всегда необходимо выполнять проверку найденных корней, подставляя их в
исходное уравнение, чтобы исключить посторонние решения.

6.

Показательные уравнения и неравенства
1
2
3
Уравнения
Показательные уравнения вида a^(f(x)) = a^(g(x)), где основание 'a' больше нуля и не равно единице, решаются путем
приравнивания показателей степеней: f(x) = g(x).
Пример
Для уравнения 2^(x+1) = 4, представляем 4 как 2²: 2^(x+1) = 2². Затем приравниваем показатели: x + 1 = 2, откуда x = 1.
Неравенства
При решении показательных неравенств a^(f(x)) > a^(g(x)), если a > 1, то f(x) > g(x); если 0 < a < 1, то знак неравенства
меняется на противоположный: f(x) < g(x).

7.

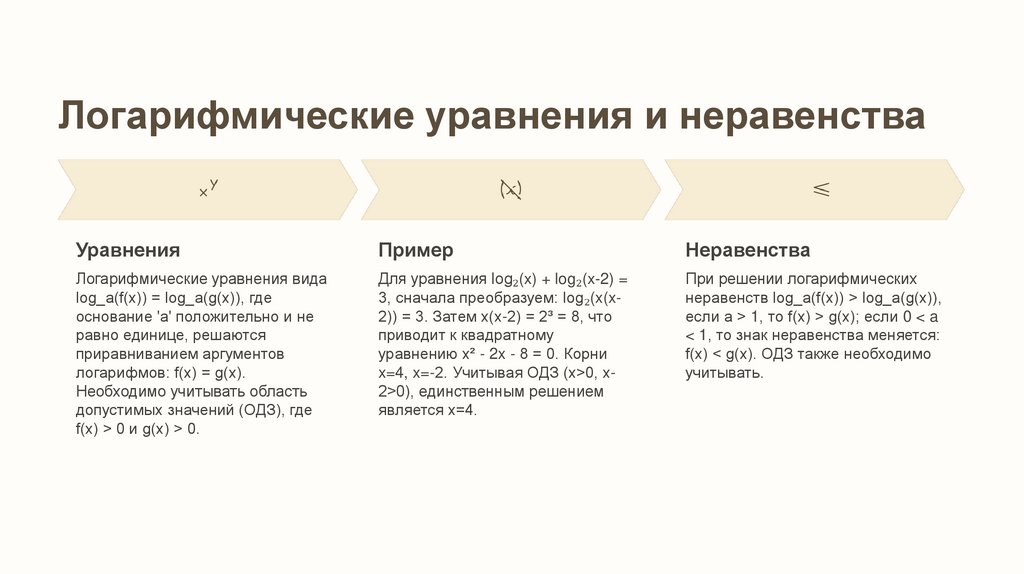
Логарифмические уравнения и неравенства
Уравнения
Пример
Неравенства
Логарифмические уравнения вида
log_a(f(x)) = log_a(g(x)), где
основание 'a' положительно и не
равно единице, решаются
приравниванием аргументов
логарифмов: f(x) = g(x).
Необходимо учитывать область
допустимых значений (ОДЗ), где
f(x) > 0 и g(x) > 0.
Для уравнения log₂(x) + log₂(x-2) =
3, сначала преобразуем: log₂(x(x2)) = 3. Затем x(x-2) = 2³ = 8, что
приводит к квадратному
уравнению x² - 2x - 8 = 0. Корни
x=4, x=-2. Учитывая ОДЗ (x>0, x2>0), единственным решением
является x=4.
При решении логарифмических
неравенств log_a(f(x)) > log_a(g(x)),
если a > 1, то f(x) > g(x); если 0 < a
< 1, то знак неравенства меняется:
f(x) < g(x). ОДЗ также необходимо
учитывать.

8.

Системы уравнений
Определение
Пример
Система уравнений представляет собой совокупность
двух или более уравнений, содержащих несколько
неизвестных, решение которой удовлетворяет всем
уравнениям одновременно. Основные методы решения
включают метод подстановки и метод сложения (или
исключения переменных).
Рассмотрим систему: x + y = 5 и x - y = 1. Применяя метод
сложения, складываем уравнения: (x + y) + (x - y) = 5 + 1,
что дает 2x = 6, откуда x = 3. Подставляем x = 3 в первое
уравнение: 3 + y = 5, получаем y = 2. Решение системы:
(3; 2).

9.

Системы неравенств
1
2
3
Определение
Система неравенств — это совокупность двух или более
неравенств. Решение системы находится как пересечение
множеств решений каждого отдельного неравенства.
Пример 1
Для системы x > 2 и x < 5, пересечением решений является
интервал (2; 5), то есть все числа, большие 2 и меньшие 5.
Пример 2
Решением системы x ≥ 1 и x ≤ 3 является отрезок [1; 3],
включающий числа от 1 до 3 включительно.

10.

Прикладные задачи
Решение уравнений и неравенств находит широкое применение во
многих прикладных областях, таких как физика, химия, экономика и
инженерия. Построение математических моделей позволяет
описывать реальные явления и процессы, а точное решение
полученных уравнений и неравенств обеспечивает возможность
прогнозирования и управления этими процессами, что критически
важно для практического применения знаний.