Динамические структуры данных

1. Динамические структуры данных

2. ЛОСС

• Линейный однонаправленный связанный
список – динамическая структура, в которой
данные представляются в виде цепочки.
• Основная идея такого способа
представления данных – элементы
структуры данных распределяются в памяти
ЭВМ в произвольном месте, но с указанием
того места, где находится следующий за
ним элемент.

3. ЛОСС

• Такой способ представления данных имеет
преимущество перед использованием
статического массива данных или записи,
поскольку обеспечивает быстрое
выполнение операций вставки и удаления
элемента данных.
• Кроме того, память, отводимая для
хранения вектора может использоваться
весьма неэффективно

4. ЛОСС

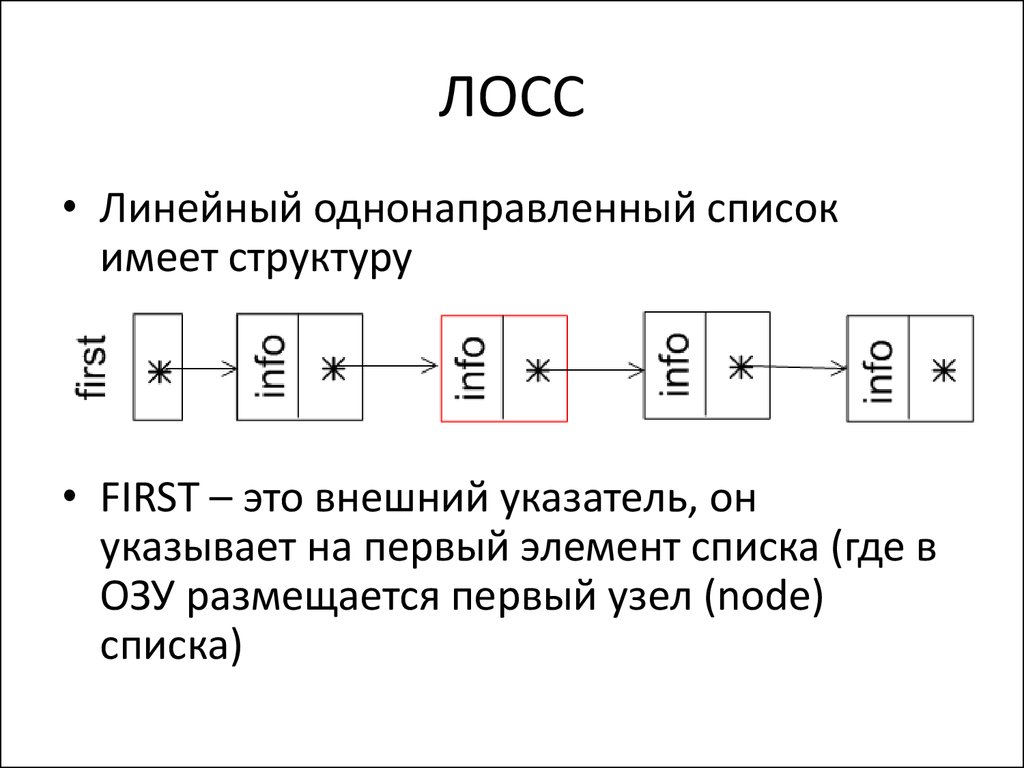
• Линейный однонаправленный список
имеет структуру
• FIRST – это внешний указатель, он
указывает на первый элемент списка (где в
ОЗУ размещается первый узел (node)
списка)

5.

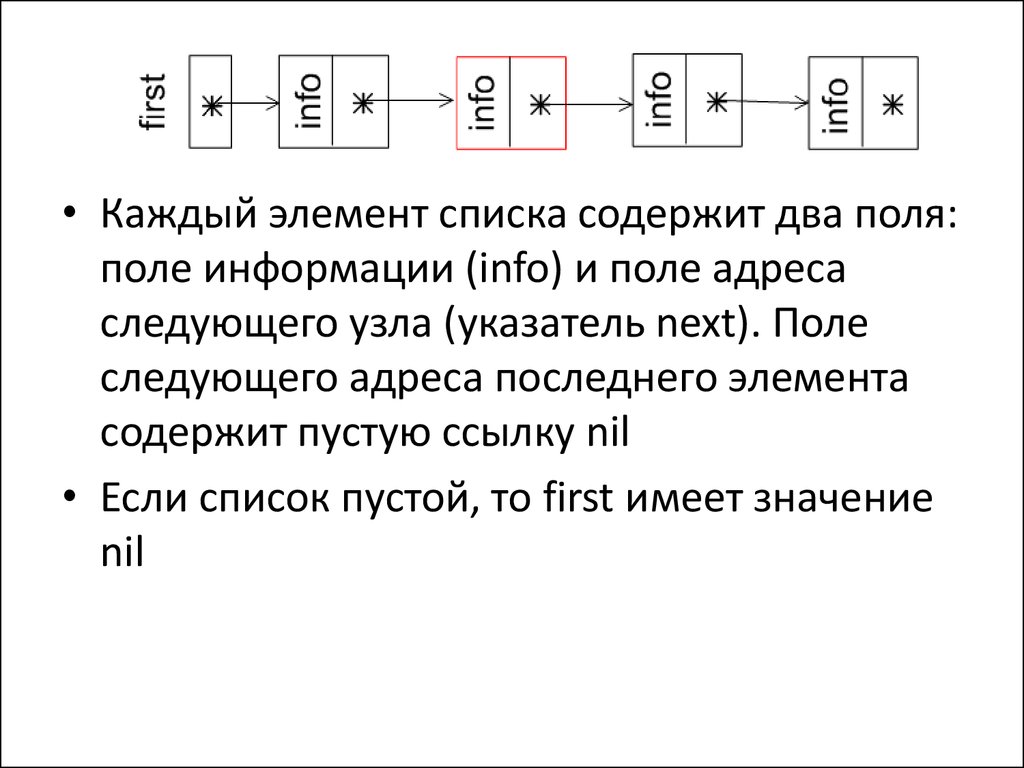
• Каждый элемент списка содержит два поля:
поле информации (info) и поле адреса
следующего узла (указатель next). Поле
следующего адреса последнего элемента
содержит пустую ссылку nil
• Если список пустой, то first имеет значение
nil

6. ЛОСС

• Определим функциональную спецификацию
структуры данных ЛОССТ: (в информационной
части узла info находятся данные типа T):
• Создать_список: → ЛОССТ
• Список_пуст: ЛОССТ → лог
• Добавить: ЛОССТ х Т → ЛОССТ
• Удалить: ЛОССТ → ЛОССТ х Т
• Первый: ЛОССТ → Т

7. ЛОСС на паскале

• После введения функциональной спецификации
структуры данных переходим к ее логическому
описание на основе одного из ЯП, например на
паскале
• Вводим тип указателя и тип узла
• Type link = ^node;
node = record
info : T;
next : link;
end;
• Var first, ptr : link; {описание внешнего и рабочего
указателей}

8. Логическое описание ЛОСС

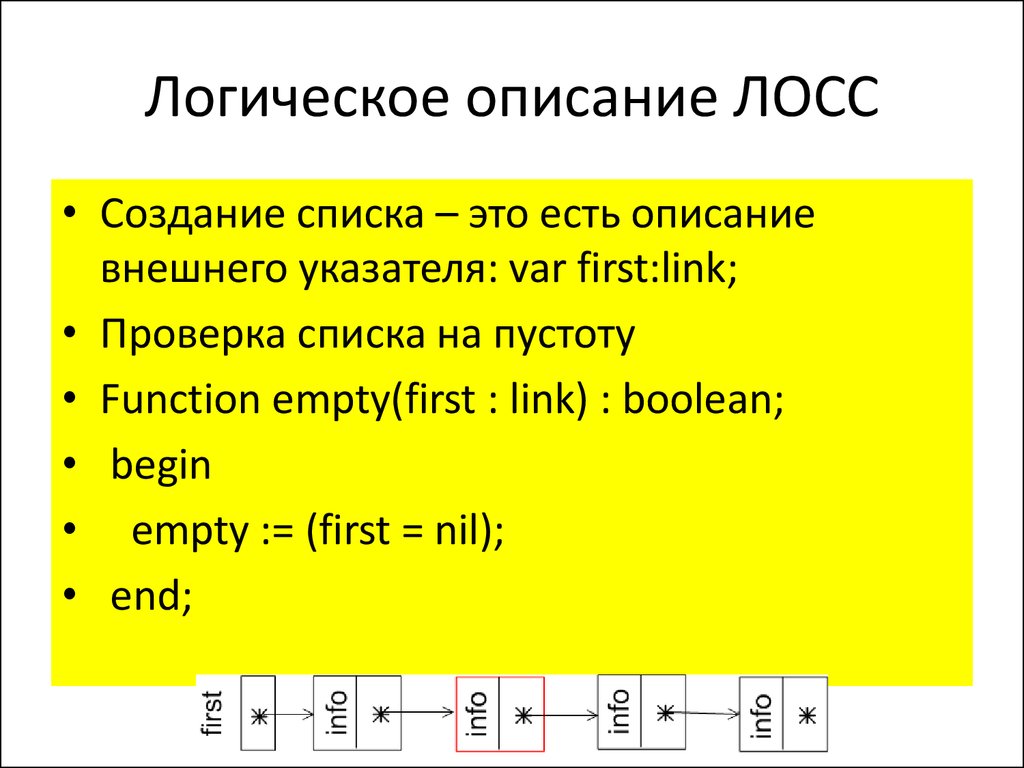
• Создание списка – это есть описание
внешнего указателя: var first:link;
• Проверка списка на пустоту
• Function empty(first : link) : boolean;
• begin
• empty := (first = nil);
• end;

9. Логическое описание ЛОСС

• Функция «Первый» - показать
информационную часть первого узла
• Function show_first(first : link) : T;
• begin
• if not empty(first) then
show_first := first^.info
• else
writeln(‘Нет первого узла’)
• end;

10. Логическое описание ЛОСС

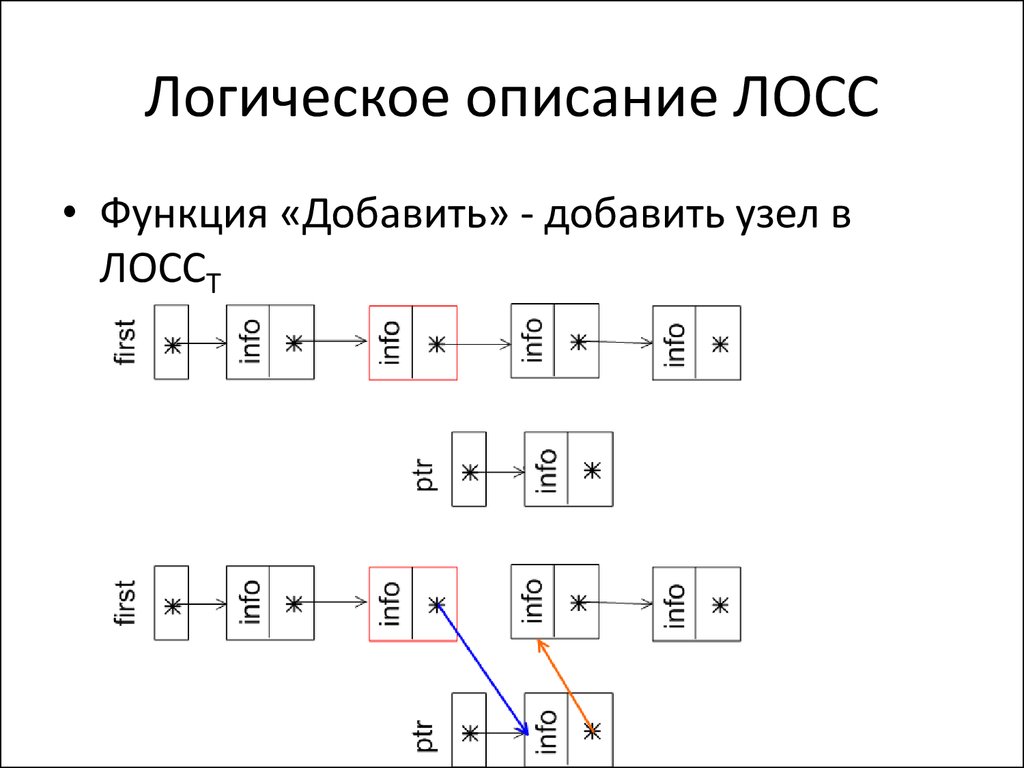
• Функция «Добавить» - добавить узел в
ЛОССТ

11.

• Procedure Add_node(var q:link; data:T);
• var ptr:link;
• begin
new(ptr); ptr^.info := data;
ptr^.next := q^.next;
q^.next := ptr;
end;

12. Формирование списка

Read(data); {читаются данные типа Т}
New(first); first^.info := data;
first^.next := nil;
ptr := first;
While <условие> do
begin
read(data); new (ptr^.next);
ptr := ptr^.next;
ptr^.info := data; ptr^.next := nil;
end;

13.

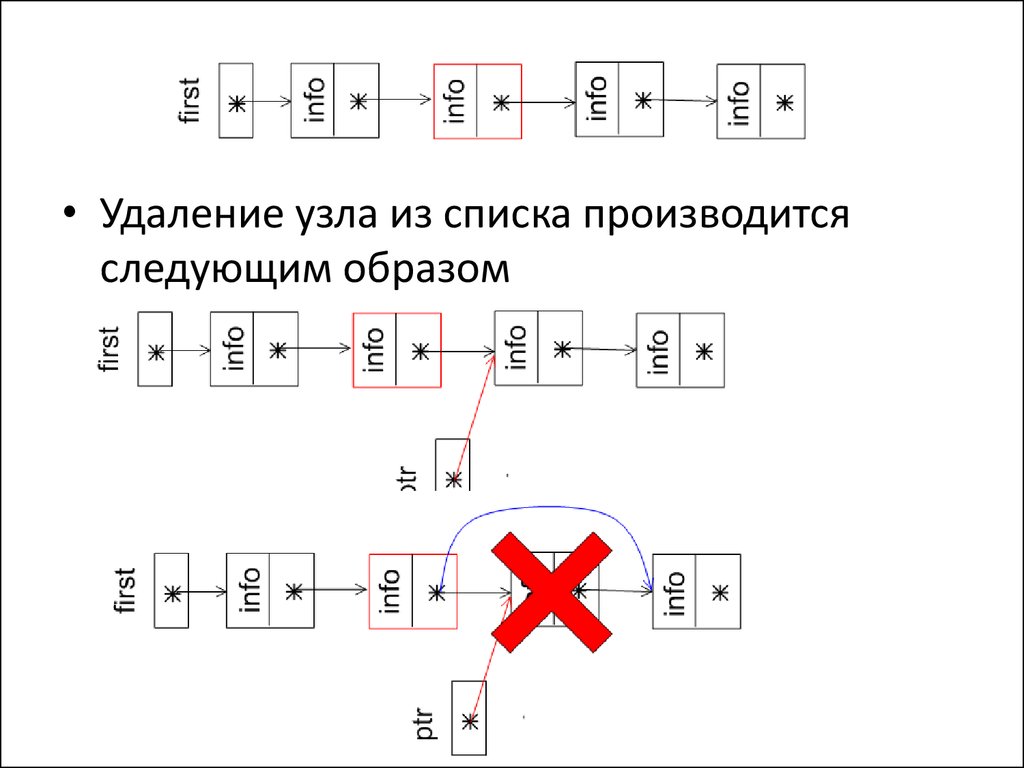
• Удаление узла из списка производится
следующим образом

14.

• Procedure Delete_node(q:link);
• var ptr:link;
• begin
ptr := q^.next;
q^.next := ptr^.next;
dispose(ptr);
end;

15. Стек

• Стек – упорядоченный набор элементов, в
котором размещение новых и удаление
существующих элементов производится
только с одного его конца, называемого
вершиной стека
• В стеке последний размещенный элемент
удаляется первым – First In - Last Out

16. Стек

• Стек применяется при синтаксическом
анализе текста, выполняемом в
трансляторах ЯП , при вызове рекурсивной
функции или процедуры

17. Функциональная спецификация

• Для структуры данных СТЕКТ можно ввести
следующую спецификацию
• Создание_стека: → СТЕКТ
• Стек_пуст: СТЕКТ → лог
• Засылка: Т х СТЕКТ → СТЕКТ
• Выборка: СТЕКТ → Т х СТЕКТ
• Последний: СТЕКТ → Т

18. Логическое описание

• Логическое описание стека
• осуществляется теми же средствами,
• что и ЛОСС.

19. Очередь

• Очередью называется упорядоченный
набор элементов, которые могут удаляться
с одного ее конца (наз. Началом очереди),
и помещаться в другой конец этого набора
(наз. Концом очереди).
• Пришедший первым уходит первым –
First In – First Out
• Логическое описание типа ОчередьТ
строится аналогично ЛОССТ и стеку

20. Очередь

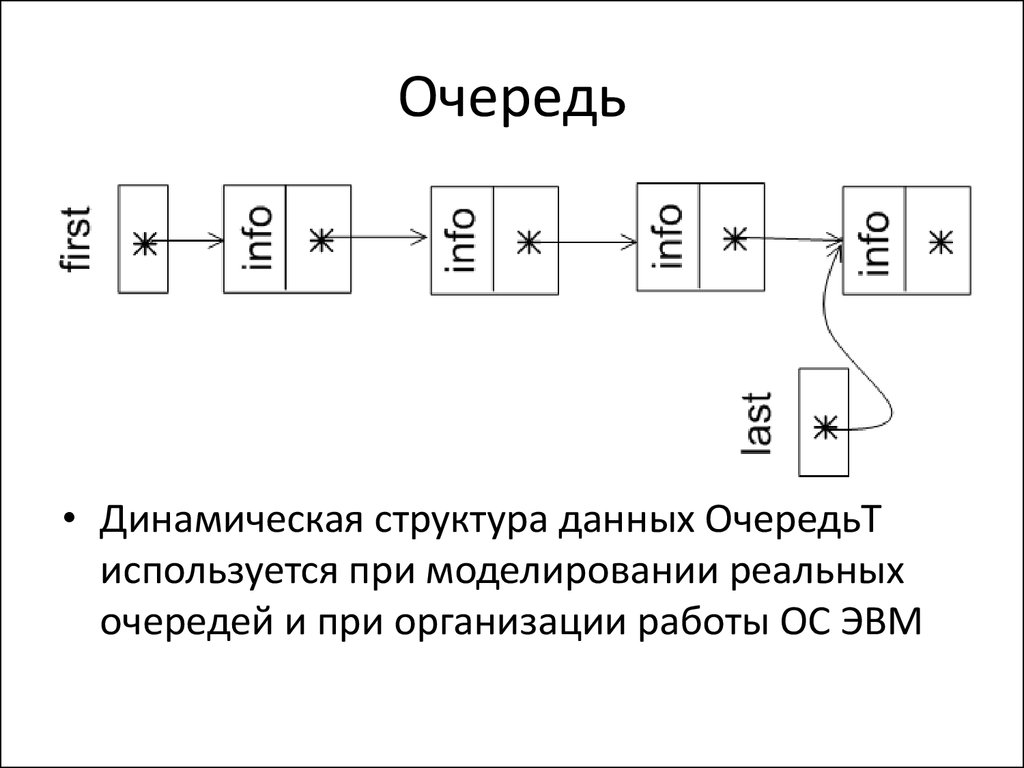
• Динамическая структура данных ОчередьТ
используется при моделировании реальных
очередей и при организации работы ОС ЭВМ

21. Дек

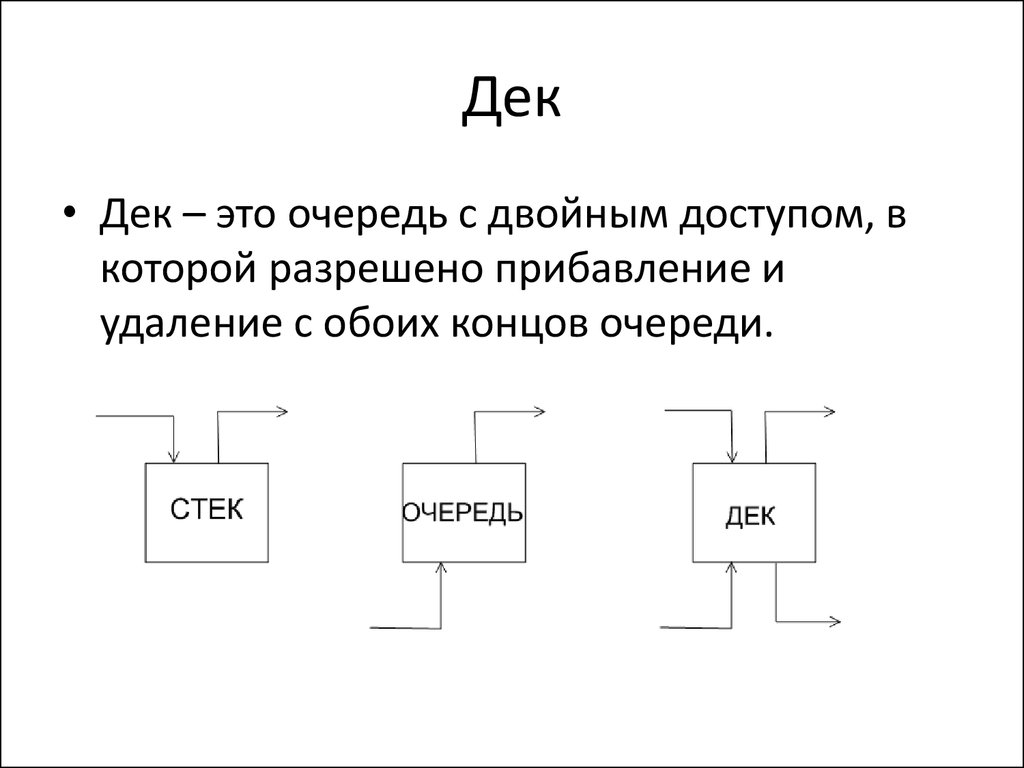
• Дек – это очередь с двойным доступом, в
которой разрешено прибавление и
удаление с обоих концов очереди.

22. Деревья

• Деревья наилучшим образом
приспособлены для решения задач
искусственного интеллекта и
синтаксического анализа текста.
• Примеры применения: программа игры в
шашки или шахматы, докозательство
теоремы, анализ зрительных или звуковых
образов

23. Деревья

• Деревом типа Т называется структура
данных, которая образована данным типа
Т, называемым корнем дерева, и
конечным, возможно пустым множеством с
переменным числом элементов – деревьев
типа Т, называемых поддеревьями этого
дерева (рекурсивное определение)

24. Деревья (терминология)

• Лист – это корень поддерева, не имеющего,
в свою очередь, поддеревьев
• Вершина – это корень подерева. Кореь и
листья дерева являются особыми
вершинами
• Вершина связана с каждым из своих
поддеревьев ветвью

25. Двоичное дерево

• Двоичным деревом типа Т называют
структуру, которая либо пуста либо
образована:
• - данным типа Т, называемым корнем
двоичного дерева
• - двоичным деревом типа Т, называемым
левым поддеревом двоичного дерева
• - двоичным деревом типа Т, называемым
правым поддеревом двоичного дерева

26. Двоичное дерево

Функциональная спецификация ДДТ:
Создание_дерева : → ДДТ
Дерево_пусто : ДДТ → лог
Чтение_корня : ДДТ → Т
Слева : ДДТ → ДДТ
Справа : ДДТ → ДДТ
Построение Т х ДДТ Х ДДТ → ДДТ

27. Двоичное дерево (логическое описание)

• При представлении данных в виде
двоичного дерева будем считать, что
каждое звено (вершина дерева) будет
записью, содержащей четыре поля: ключ
записи, ссылка на левое поддерево, ссылка
на правое поддерево и информационная
часть.

28. Построение двоичного дерева

• Рассмотрим принцип построения дерева
при занесении записей в таблицу. Пусть в
первоначально пустую таблицу заносится
последовательно поступающие записи с
ключами 70, 60, 85, 87, 90, 45, 30, 88, 35, 20,
86.
• Если ключ следующей записи окажется
меньше k, то этой записи поставим в
соответствие левую вершину, в противном
случае – правую.