2025-Лекция 1 по дисциплине АССОД_270303_Мошкин_7 семестр

1. Автоматизированные системы сбора и обработки данных

АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ
СБОРА И ОБРАБОТКИ ДАННЫХ
ФИО преподавателя: Мошкин Владимир Валентинович
e-mail: moshkin@mirea.ru
Online-edu.mirea.ru
1

2. Лекция 1

Методы и средства измерений
2

3. Содержание

1.1. Классификация измерений
1.2. Методы измерений
1.3. Единицы физических величин и их системы
1.4. Погрешности измерений
1.5. Виды средств измерений и их основные
характеристики
3

4. Определение измерения

Важнейшим способом получения информации о количественных
свойствах объектов являются измерения.
Информация, которая получается в результате измерений, называется
измерительной информацией.
Измерения основываются на экспериментальных процедурах, поэтому
для их выполнения необходимо располагать специальными техническими
средствами. Эти средства называются средствами измерений, а для
описания их свойств используется комплекс специальных характеристик,
которые называются метрологическими характеристиками и позволяют
судить о пригодности средств измерений для практического
использования.
Таким образом, измерение – это нахождение значения физической
величины опытным путем с помощью специальных технических средств.
4

5. Классификация измерений

Измерения классифицируют по целому ряду признаков:
По характеристике точности:
Равноточные измерения – ряд измерений какой-либо величины,
выполненных одинаковыми по точности средствами измерений в одних и тех
же условиях.
Неравноточные измерения – ряд измерений какой-либо величины,
выполненных различными по точности средствами измерений и (или) в
разных условиях.
По числу измерений, выполняемых в серии:
Однократное измерение – измерение, выполненное один раз.
Основным условием, при котором такое измерение в принципе возможно,
является наличие априорной информации о точности полученного отсчета.
Многократное измерение – измерение, результат которого получают
из нескольких следующих друг за другом однократных измерений.
Многократные измерения одной и той же величины постоянного размера
производятся при повышенных требованиях к точности измерений.
5

6. Классификация измерений

По характеру изменения во времени измеряемой величины:
Статическое измерение – измерение, на протяжении времени которого
измеряемая величина принимается неизменной.
Динамическое измерение – измерение, на протяжении времени которого
измеряемая величина принимается переменной.
По способу представления результатов измерений:
Абсолютное измерение – измерение, приводящее к значению,
основанному на прямых измерениях одной или нескольких основных величин.
Результат прямых измерений выражается в единицах измеряемой величины,
например, определение длины в метрах, силы электрического тока в амперах.
Относительное измерение – измерение отношения измеряемой
величины к одноименной величине, играющей роль единицы или измерение
величины по отношению к одноименной величине, принимаемой за исходную.
Например, при измерении относительной влажности воздуха, ее определяют как
отношение количества водяных паров в 1 куб. см воздуха к количеству водяных
паров, которое насыщает 1 куб. см воздуха при данной температуре.
6

7. Классификация измерений

По способу получения (обработки) результатов измерений:
Прямое измерение – измерение, при котором искомое значение
физической величины получают непосредственно из опытных данных,
например, измерение температуры тела термометром, силы тока –
амперметром, длительности временного интервала – секундомером.
Косвенное измерение – измерение, при котором искомое значение
физической величины определяют на основании известной зависимости
между искомой величиной и другими величинами, значения которых
получают в результате прямых измерений. Например, сопротивление
резистора R находят из уравнения R=U / I, где падение напряжения на
резисторе – U и ток через него – I находят в результате прямых измерений.
7

8. Классификация измерений

Совокупные измерения – измерения нескольких однородных величин
в различных их сочетаниях, при которых искомую величину определяют
решением системы уравнений. Например, измеряя сопротивления Rab, Rac
и Rbc между различными вершинами треугольника, в котором соединены
сопротивления R1, R2 и R3 и, решая систему уравнений можно определить
искомые значения сопротивлений R1, R2 и R3 методом совокупных
измерений.
8

9. Классификация измерений

Совместные измерения – одновременные измерения двух или более
неоднородных величин для нахождения зависимости между ними.
Например, измеряя сопротивление резистора при трех различных
температурах, составляют систему из трех уравнений с целью нахождения
параметров R0, A и B с помощью известной зависимости сопротивления
резистора от температуры:
где T0 - температура, при которой определяется значение R0,
A и B - температурные коэффициенты сопротивления,
T1, T2, T3 – значения температуры при измерениях.
9

10. Содержание

1.1. Классификация измерений
1.2. Методы измерений
1.3. Единицы физических величин и их системы
1.4. Погрешности измерений
1.5. Виды средств измерений и их основные
характеристики
10

11. Методы измерений

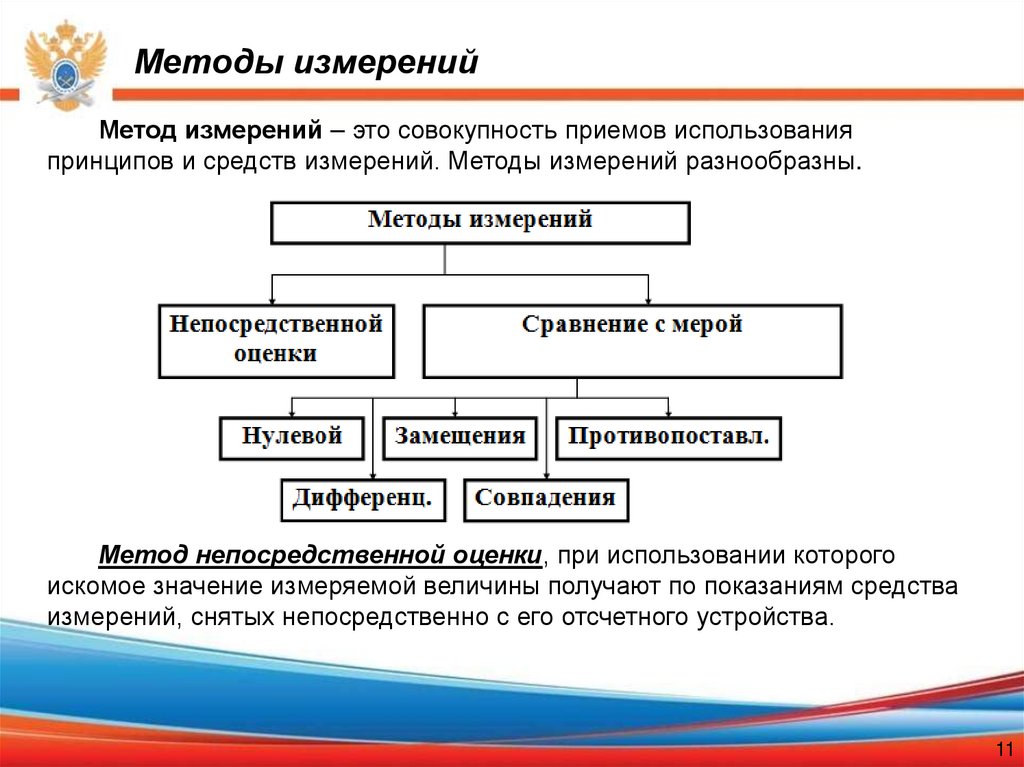
Метод измерений – это совокупность приемов использования
принципов и средств измерений. Методы измерений разнообразны.
Метод непосредственной оценки, при использовании которого
искомое значение измеряемой величины получают по показаниям средства
измерений, снятых непосредственно с его отсчетного устройства.
11

12. Методы измерений

Метод сравнения с мерой, при использовании которого искомое значение
измеряемой величины получают в результате ее сравнения с величиной,
воспроизводимой мерой. Разновидности метода сравнения с мерой:
- Нулевой метод характеризуется тем, что измеряемая величина
одновременно или периодически сравнивается с мерой, и результирующий
эффект воздействия этих величин на устройство сравнения доводится до нуля.
Используемая в нулевом методе измерений мера должна быть изменяемой
(регулируемой), а точность метода тем выше, чем выше чувствительность
устройства сравнения.
- Метод замещения характеризуется тем, что измеряемую величину
замещают известной величиной, воспроизводимой мерой. Например,
измерение сопротивления омметром с поочередным подключением к нему
измеряемого сопротивления и образцового магазина сопротивлений
(регулируемая мера). Сопротивление магазина, при котором показания омметра
такие же, как при измерении искомого сопротивления, равно измеряемому
значению.
12

13. Методы измерений

- Метод противопоставления характеризуется тем, что измеряемая
величина и величина, воспроизводимая мерой, одновременно воздействуют на
устройство сравнения, с помощью которого устанавливается соотношение
между величинами. Примером реализации этого метода является измерение
массы на равноплечих весах с использованием уравновешивающих гирь.
- Дифференциальный метод характеризуется тем, что на средство
измерений воздействует разность между измеряемой величиной и известной
величиной, воспроизводимой нерегулируемой мерой. Этот метод, при условии
высокой точности воспроизведения величины мерой, позволяет получить
хорошую точность измерений даже в случае применения относительно
неточных средств измерений.
- Метод совпадений характеризуется тем, что разность значений с
размером измеряемой величины и величины, воспроизводимой мерой,
определяют, используя совпадение отметок шкал или периодических сигналов.
Например, при измерении длины с помощью штангенциркуля с нониусом
наблюдают совпадение отметок на шкалах штангенциркуля и нониуса.
13

14. Содержание

1.1. Классификация измерений
1.2. Методы измерений
1.3. Единицы физических величин и их системы
1.4. Погрешности измерений
1.5. Виды средств измерений и их основные
характеристики
14

15. Единицы физических величин

Для получения результата измерений следует сравнить измеряемую
величину с единицей измерения, т.е. физически однородной ей величиной,
числовое значение которой равно единице. Результат такого сравнения можно
записать в виде:
Q
q
Q
где Q – значение измеряемой величины,
[Q] – единица измерения,
q– числовое значение измеряемой величины в принятых единицах
измерения.
Эта формула, записанная в виде: Q=q [Q], называется основным
уравнением измерения.
Единица измерения должна быть установлена для каждой из известных
физических величин.
15

16. Единицы физических величин

Многие физические величины связаны между собой функциональными
зависимостями. Поэтому только часть физических величин и соответственно их
единиц могут определяться независимо от других.
Такие величины называют основными. Остальные физические величины
(их принято называть производными) определяются с использованием
физических законов и зависимостей через основные физические величины.
Всю совокупность физических величин принято рассматривать как систему.
Система единиц физических величин – это совокупность основных и
производных физических величин системы, образованных в соответствии с
принятыми принципами, например, система СИ.
Внесистемная единица физической величины – единица физической
величины, не входящая ни в одну из принятых систем единиц, например,
единица длины дюйм, единица энергии квт-час.
В системе СИ кроме основных и производных единиц имеются две
дополнительные единицы для измерения плоского и объемного углов.
16

17. Основные единицы физических величин системы СИ

1. Метр равен длине пути, проходимого светом в вакууме за 1/299792458
долю секунды.
2. Килограмм равен массе международного прототипа килограмма.
3. Секунда равна 9192631770 периодам излучения, соответствующего
переходу между двумя сверхтонкими уровнями основного состояния атома
цезия - 133.
4. Ампер равен силе неизменяющегося тока, который при прохождении по
двум прямолинейным параллельным проводникам бесконечной длины и
ничтожно малой площади кругового сечения, расположенным на расстоянии 1м
один от другого в вакууме, вызывает на каждом участке проводника длиной 1 м
силу взаимодействия, равную 2 Н.
5. Кельвин равен 1/(273,16) части термодинамической температуры тройной
точки воды.
6. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг.
7. Кандела равна силе света в заданном направлении от источника,
испускающего монохроматическое излучение частотой 540 Гц, энергетическая
сила света которого в этом направлении составляет 1/683 Вт/ср.
17

18. Дополнительные единицы системы СИ

Угловые единицы не могут быть введены в число основных, так как это
вызвало бы затруднение в трактовке размерностей величин, связанных с
вращением (дуги окружности, площади круга, работы пары сил и т.д.). Вместе с
тем они не являются и производными единицами, так как не зависят от выбора
основных единиц.
Единица плоского угла – радиан (рад). Один радиан это угол между
двумя радиусами окружности, дуга между которыми по длине равна радиусу. В
градусном исчислении радиан равен 57 17 44,8 .
Стерадиан (ср), принимаемый за единицу телесного угла, это телесный
угол, вершина которого расположена в центре сферы, и который вырезает на
поверхности сферы площадь, равную площади квадрата со стороной, по длине
равной радиусу сферы.
Измеряют телесные углы путем определения плоских углов и проведения
дополнительных расчетов по формуле
2 1 cos
2
где - телесный угол, - плоский угол при вершине конуса, образованного
внутри сферы данным телесным углом. Телесному углу 1 ср соответствует
плоский угол, равный 65 32 , углу ср - плоский угол 120 , углу 2 ср - плоский
угол 180 .
18

19. Содержание

1.1. Классификация измерений
1.2. Методы измерений
1.3. Единицы физических величин и их системы
1.4. Погрешности измерений
1.5. Виды средств измерений и их основные
характеристики
19

20. Классификация погрешностей

Отклонение результата измерения от истинного значения измеряемой
величины называется погрешностью измерения.
По способу числового выражения различают абсолютную и
относительную погрешности.
Абсолютная погрешность выражается в единицах измеряемой
физической величины:
= х - хи
где х - значение, полученное при измерении; хи - истинное значение
измеряемой величины.
Относительная погрешность отн, равна отношению абсолютной
погрешности измерения к истинному значению измеряемой величины:
20

21. Классификация погрешностей

В зависимости от характера проявления погрешности делят на
систематические и случайные.
Систематической погрешностью измерения называется
составляющая погрешности измерения, остающаяся постоянной или
закономерно изменяющаяся при повторных измерениях одной и той же
физической величины. Причиной появления систематических погрешностей
могут быть неисправности измерительной аппаратуры, несовершенство метода
измерения, неправильная установка измерительных приборов и отступление от
нормальных условий их работы, особенности и неправильные действия самого
оператора.
Случайной погрешностью измерения называется составляющая
погрешности измерения, изменяющаяся случайным образом при повторных
измерениях одной и той же физической величины. Наличие случайных
погрешностей выявляется при проведении ряда измерений этой величины,
когда оказывается, что результаты измерений не совпадают друг с другом.
21

22. Причины появления систематических погрешностей

Возникновение систематических погрешностей обусловлено несовпадением принятых моделей объекта, средства измерения и измерительного
процесса с реальными условиями.
В соответствии с причинами возникновения погрешности подразделяют на:
- методические,
- инструментальные,
- субъективные.
Методические погрешности происходят от несовершенства метода
измерения, упрощающих предположений и допущений при выводе
применяемых формул, влияния измерительного прибора на объект измерения.
В любом случае информацию о значении методической погрешности
нельзя получить из нормативно-технической документации на средство
измерения, т.к. методическая погрешность либо совсем не зависит от
характеристик средства измерения, либо проявляется в каждом конкретном
случае в различной степени.
22

23. Причины появления систематических погрешностей

Инструментальные погрешности измерения зависят от погрешностей
применяемых средств измерения: приборов, преобразователей, мер и т.п.
Неточность градуировки, конструктивные несовершенства, изменения
характеристик прибора в процессе эксплуатации и некоторые другие причины
вызывают появление инструментальных погрешностей.
Для каждого средства измерения в паспорте указывается максимально
допустимое значение погрешности измерения в виде класса точности. Это
нужно учитывать при выборе средства измерения при проведении
измерительных процедур.
Субъективные погрешности вызываются неправильными отсчетами
показаний прибора человеком (оператором). Это может случиться, например,
из-за неправильного направления взгляда при наблюдении за показаниями
стрелочного прибора (погрешность от параллакса). Использование цифровых
приборов и автоматических методов измерения позволяет исключить такого
рода погрешности. Компьютерные измерения также свободны от них.
23

24. Методы устранения систематических погрешностей

Существуют специальные методы организации измерений, устраняющие
систематические погрешности. К ним относятся, например, метод замещения и
метод компенсации по знаку.
Метод замещения заключается в том, что измеряемая величина
замещается одноименной величиной, получаемой при помощи регулируемой
меры. Если такое замещение производится без каких-либо других изменений в
экспериментальной установке и после замещения установлены те же показания
приборов, то значение измеряемой величины равняется значению, которое
отсчитывается по указателю регулируемой меры.
Метод компенсации по знаку применяется для исключения
систематических погрешностей, которые в зависимости от условий измерения
могут входить в результат измерения с тем или иным знаком (погрешность от
термо-ЭДС, от влияния напряженности постоянного электрического или
магнитного поля и др.). В этом случае нужно провести измерения дважды: так,
чтобы погрешность в результаты измерений входила один раз с одним знаком, а
в другой раз - с обратным. Среднее значение из двух полученных результатов
является окончательным результатом измерения, свободным от указанных
выше систематических погрешностей.
24

25. Исправление результата измерения

Обнаружение причин и источников систематических погрешностей
позволяет принять меры к их устранению либо исключению посредством
введения поправки.
Поправкой называется значение величины, одноименной с измеряемой,
которое нужно прибавить к полученному при измерении значению величины с
целью исключения систематической погрешности. Таким образом, поправка
численно равна абсолютной погрешности измерения, взятой с
противоположным знаком.
В некоторых случаях используют поправочный множитель – число, на
которое надо умножить результат измерения, чтобы исключить
систематическую погрешность.
Поправка или поправочный множитель определяются при помощи поверки
технического средства, составления и использования соответствующих таблиц
и графиков, Применяются также расчетные способы нахождения поправочных
значений.
25

26. Случайные погрешности и их оценка

Случайная величина в целом задается генеральной совокупностью.
Генеральная совокупность - это полный набор всех возможных значений, которые
может принимать случайная величина в ходе эксперимента. Генеральная совокупность
может быть конечной и реально существующей или бесконечной, гипотетической.
Рассчитать значения числовых характеристик генеральной совокупности можно
только в том случае, если вся генеральная совокупность находится в распоряжении
исследователя, что на практике не реально. Поэтому характеристики генеральной
совокупности оцениваются на основе конечного набора значений случайной величины,
называемого выборкой.
Генеральная совокупность обладает некоторыми неслучайными свойствами, которые
надо выявить в результате эксперимента. Исчерпывающей характеристикой случайной
величины Х (а следовательно, и ее генеральной совокупности) является функция
распределения F(x), равная вероятности того, что в результате эксперимента эта
случайная величина Х примет значение меньшее, чем х. Таким образом:
F(x) = P(X x).
Если функция распределения имеет производную, то функция
называется плотностью распределения.
f(x) = F (x)
Функция распределения F(x) и плотность распределения f(x) характеризуют всю
генеральную совокупность и являются детерминированными, неслучайными функциями,
имеющими вполне конкретный аналитический и графический вид.
26

27. Случайные погрешности и их оценка

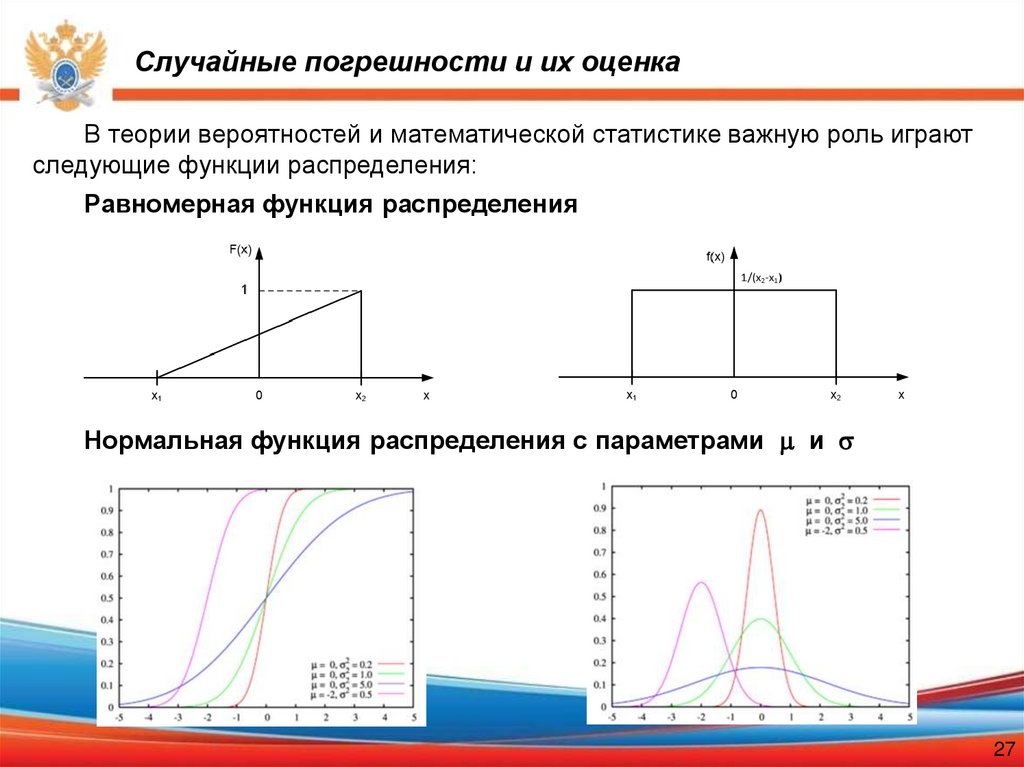
В теории вероятностей и математической статистике важную роль играют
следующие функции распределения:
Равномерная функция распределения
Нормальная функция распределения с параметрами и
27

28. Случайные погрешности и их оценка

Важнейшими числовыми характеристикам случайной величины являются ее
2
математическое ожидание M̂[X] и дисперсия ˆ [ X ] (параметр ̂ называется средним
квадратическим отклонением случайной величины).
Если выборка состоит из N результатов измерений, то в качестве оценки
математического ожидания используется среднее арифметическое значение:
,
а оценка дисперсии вычисляется по формуле:
Определив оценку среднего квадратического отклонения и задав величину
доверительной вероятности Р (обычно берут Р = 0,95), можно вычислить абсолютную
погрешность результата измерения физической величины:
Δ = zP· ̂ ,
где zP – квантиль закона распределения случайной величины, определяемый по
таблице распределения для заданной доверительной вероятности P.
В итоге можно записать результат измерения в виде: X = x
±Δ,P
28

29. Содержание

1.1. Классификация измерений
1.2. Методы измерений
1.3. Единицы физических величин и их системы
1.4. Погрешности измерений
1.5. Виды средств измерений и их основные
характеристики
29

30. Виды средств измерений

Средством измерений называется техническое средство,
предназначенное для измерений, имеющее нормированные
метрологические характеристики, воспроизводящее и (или)
хранящее единицу физической величины, размер которой
принимают неизменным (в пределах установленной погрешности) в
течение известного интервала времени.
Согласно межгосударственным рекомендациям РМГ 29-99
«Метрология. Основные термины и определения» СИ подразделяются на виды:
Мера – средство измерений, предназначенное для
воспроизведения и (или) хранения физической величины одного
или нескольких заданных размеров, значения которых выражены в
установленных единицах и известны с необходимой точностью.
30

31. Виды средств измерений

Измерительный преобразователь – техническое средство с
нормированными метрологическими характеристиками, служащее
для преобразования измеряемой величины в другую величину или
измерительный сигнал, удобный для обработки, хранения,
дальнейших преобразований, индикации или передачи.
Измерительный прибор – средство измерений,
предназначенное для получения значений измеряемой физической
величины в установленном диапазоне в форме, доступной для
непосредственного восприятия наблюдателем.
Измерительная система – совокупность функционально
объединенных мер, измерительных приборов, измерительных
преобразователей, ЭВМ и других технических средств,
размещенных в разных точках контролируемого объекта, с целью
измерений одной или нескольких физических величин,
свойственных этому объекту, и выработки измерительных сигналов
в разных целях.
31

32. Виды средств измерений

По метрологическим функциям средства измерений подразделяются
на эталоны, образцовые средства измерений и рабочие средства
измерений.
Эталон единицы физической величины - это средство измерений
(комплекс средств измерений), обеспечивающее воспроизведение и (или)
хранение единицы физической величины с целью передачи размера
единицы образцовым, а от них рабочим средствам измерений и
утвержденное в качестве эталона. Эталоны подразделяются на первичные,
специальные и вторичные.
Образцовое средство измерений (ОСИ) – средство измерений,
предназначенное или применяемое для поверки рабочих средств измерений
или подчиненных образцовых средств измерений.
Образцовые средства измерений в зависимости от точности
подразделяются на разряды 1-ый, 2-ой и т.д.; 1-ый разряд – самый высокий.
Рабочее средство измерений - это средство измерений, используемое
в широкой измерительной практике и, в отличие от перечисленных выше
эталонов и ОСИ, не связанное с передачей единиц размера физических
величин.
32

33. Характеристики средств измерений

Все средства измерений, независимо от их конкретного назначения,
обладают рядом общих свойств. Технические характеристики,
описывающие эти свойства и оказывающие влияние на результаты и
точность измерений, называются метрологическими характеристиками.
1. Функция преобразования (статическая характеристика
преобразования) — функциональная зависимость между информативными
параметрами выходного и входного сигналов средства измерений.
Функцию преобразования, устанавливаемую в научно-технической
документации на данное средство измерений, называют номинальной
функцией преобразования.
2. Чувствительность средства измерений - отношение приращения
выходного сигнала Δу средства измерений к вызвавшему это приращение
изменению входного сигнала Δх. В общем случае чувствительность:
3. Порог чувствительности - наименьшее изменение входной
величины, обнаруживаемое с помощью данного средства измерений.
Порог чувствительности выражают в единицах входной величины.
33

34. Характеристики средств измерений

4. Диапазон измерений — область значений измеряемой величины,
для которой нормированы допускаемые погрешности средства измерений.
Диапазон измерений ограничивается наибольшим и наименьшим
значениями диапазона измерений.
5. Цена деления шкалы измерительного прибора— разность
значений величины, соответствующих двум соседним отметкам шкалы.
Для средств измерений, выдающих результаты измерений в цифровом
коде, указывают цену единицы младшего разряда (единицы младшего
разряда цифрового отсчетного устройства), вид выходного кода
(двоичный, двоично-десятичный) и число разрядов кода.
6. Входное полное сопротивление ZBX указывают для оценки
влияния средства измерений на режим работы объекта исследования.
Входное сопротивление влияет на мощность, потребляемую от объекта
исследования средством измерений.
7. Выходное полное сопротивление ZВЫХ позволяет оценить
допустимую нагрузка на средство измерений. Чем меньше выходное
сопротивление, тем больше допустимая нагрузка на средство измерений.
34

35. Характеристики средств измерений

8. Погрешность средства измерений – отличие получаемых с его
помощью результатов измерений от истинного значения измеряемой величины.
Погрешность измерительного прибора может быть выражена в виде:
- абсолютной погрешности
Δх = x-xи;
- относительной погрешности
δ = Δх/x;
- приведенной погрешности
γ = Δх/xN,
где x – показание прибора, xи – истинное значение измеряемой величины,
xN – нормирующее значение.
Погрешность измерительного прибора определяют при его поверке и при
этом вместо истинного значения используют действительное значение
измеряемой величины, найденное экспериментальным путем с помощью
образцовых средств измерений и настолько приближающееся к истинному, что
для данной цели может быть использовано вместо истинного значения.
Основной погрешностью средства измерений называют погрешность в
условиях, принятых за нормальные.
Дополнительные погрешности средства измерений возникают при
отклонении влияющих величин от нормальных значений.
35

36. Характеристики средств измерений

9. Динамические характеристики средства измерений - это
характеристики его инерционных свойств, определяющие зависимость
выходного сигнала средства измерений от меняющихся во времени величин:
параметров входного сигнала, внешних влияющих величин, нагрузки.
Полная динамическая характеристика — характеристика, однозначно
определяющая изменения выходного сигнала средства измерений при любом
изменении во времени информативного или неинформативного параметра
входного сигнала, влияющей величины или нагрузки. К полным динамическим
характеристикам относят:
- переходная характеристика,
- импульсная переходная характеристика,
- амплитудно-фазовая характеристика,
- совокупность АЧХ и ФЧХ,
- передаточная функция.
Частные динамические характеристики – отдельные функционалы или
параметры полных динамических характеристик:
- время реакции средства измерения,
- коэффициент демпфирования,
- значение резонансной собственной частоты.
36

37. Класс точности средств измерений

Для представления результата измерения в соответствии с действующими
стандартами в области метрологии необходимо указать не только само значение
измеренной величины, но и величину погрешности с которой этот результат
получен.
Важной характеристикой средства измерений является класс точности,
который определяет предел допустимой погрешности средства измерений.
Вопросы нормирования погрешностей средств измерений рассмотрены в
ГОСТ 8.401—80 «Классы точности средств измерений. Общие требования».
Согласно этому стандарту пределы допускаемых основной и
дополнительных погрешностей выражают в форме
- приведенных,
- относительных,
- абсолютных погрешностей
в зависимости от характера изменения погрешностей в пределах диапазона
измерений, а также от условий применения и назначения средств измерений.
37

38. Класс точности средств измерений

Пределы допускаемой абсолютной основной погрешности, выраженной в
единицах измеряемой величины или условно в делениях шкалы, устанавливают по
формулам:
или
x a
x a bx
,
где х — значение измеряемой величины на входе (выходе) средства измерений или
число делений, отсчитанных по шкале; а, b — положительные числа, не зависящие от х.
В первом выражении учитывается только аддитивная погрешность, которая не
зависит от результата измерения.
Во втором выражении учитывается как аддитивная так и мультипликативная
составляющие погрешности.
В этих случаях класс точности обозначается заглавными буквами латинского
алфавита (например, L, M, C и т.д.), или римскими цифрами (I, II, III, IV и т.д.), к буквам
при этом допускается присоединять индексы в виде арабской цифры. Чем меньше
пределы допускаемой погрешности, тем ближе к началу алфавита должна быть буква и
тем меньше цифра. Эти обозначения класса точности весьма неудобны, т.к. имеют
условный характер. Смысл этих обозначений раскрывается в нормативно-технической
документации на средство измерений.
38

39. Класс точности средств измерений

Пределы допускаемой приведенной основной погрешности (в процентах)
устанавливаются по формуле:
x
xN
100% p
где ΔX — пределы допускаемой абсолютной основной погрешности;
XN — нормирующее значение (условно принятое значение измеряемой величины,
выраженное в тех же единицах, что и ΔX);
р — положительное число, выбираемое из ряда:
p = 1·10n; 1,5·10n; 2·10n; 2,5·10n; 4·10n; 5·10n; 6·10n ( 1, 0, -1, -2, и т.д.)
В этих случаях класс точности совпадает численно с р и обозначается p или P
(если нормирующее значение равно длине шкалы). Это обозначение, как правило,
наносится на циферблат или корпус средства измерений и приводится в его
документах.
Правила выбора нормирующего значения XN
Тип шкалы средства измерений
Равномерная или степенная шкала и нуль на
краю диапазона измерений
Равномерная или степенная шкала и нулевой
отметкой внутри диапазона измерений
Шкала с условным нулем
Для средств измерений с установленным
номинальным значением
Существенно неравномерная шкала
Нормирующее значение
Модуль предела измерения
Сумма модулей пределов измерений
Модуль разности пределов измерений
Номинальное значение
Длина шкалы в единицах длины
39

40. Класс точности средств измерений

Пределы допускаемой относительной основной погрешности (в
процентах) устанавливаются по формуле:
отн
если
x a
x
100% q ,
x
или по формуле:
x
xк
отн
100% c d
1 ,
x
x
если x a bx .
В этих формулах - большие (по модулю) значения величин q, c и d
выбираются из того же ряда, что и при нормировании приведенной
погрешности:
1·10n; 1,5·10n; 2·10n; 2,5·10n; 4·10n; 5·10n; 6·10n ( 1, 0, -1, -2, и т.д.)
40

41. Обозначения классов точности средств измерений

41