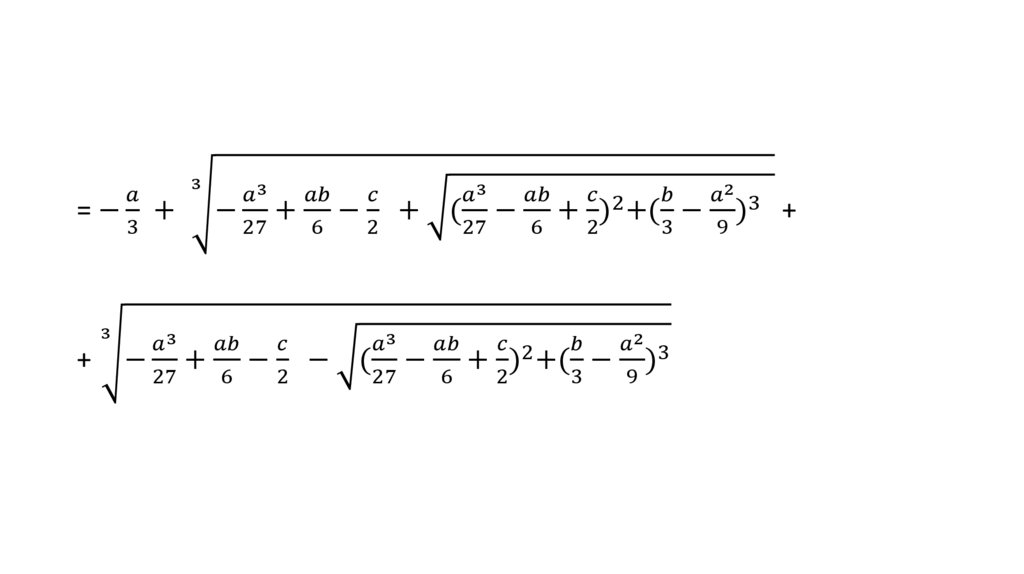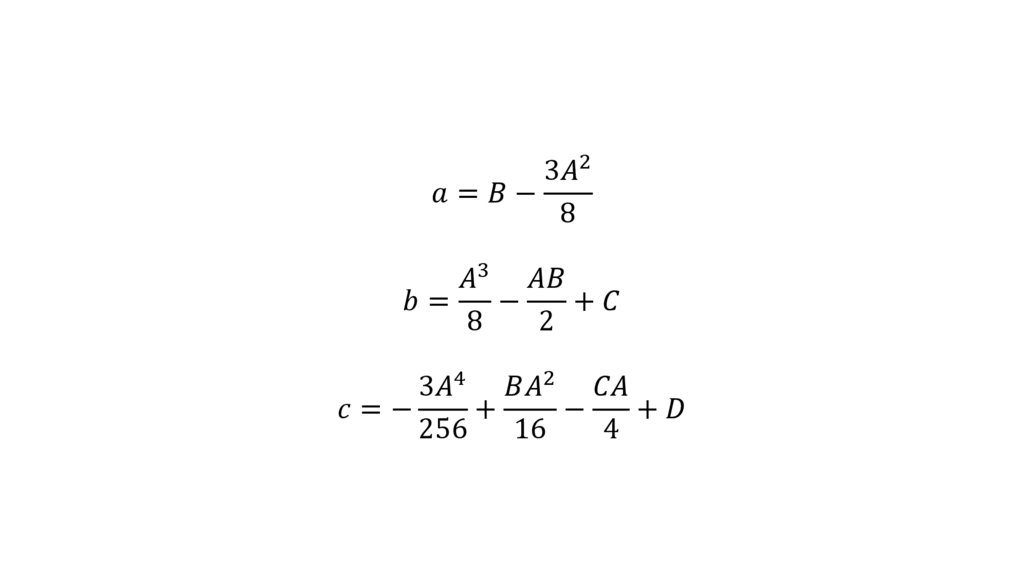Презентация Решение уравнений от 1 до 4 степени (3)

1. От одного до четырёх

Как решают уравнения от первой до четвёртой степени

2. История математических уравнений

Алгебра как искусство решать уравнения зародились очень давно
в связи с потребностью практики, в результате поиска общих
приёмов решения однотипных задач. Самые ранние дошедшие до
нас рукописи свидетельствуют о том, что в Древнем Вавилоне и
Древнем Египте были известны приёмы решения линейных
уравнений.
Знак равенства ввел в 1556 году английский математик Рекорд,
который объяснил это так, что ничто не может быть более равным,
чем два параллельных отрезка.

3. Первый случай употребления символа равенства

4. Линейное уравнение (первая степень)