Similar presentations:
8-2-3
1.
ТАБЛИЦЫ ИСТИННОСТИЛОГИЧЕСКИХ ВЫРАЖЕНИЙ
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
2.
КЛЮЧЕВЫЕ СЛОВА✦ логическая переменная
✦ логическая операция
✦ логическое выражение
✦ таблица истинности
3.
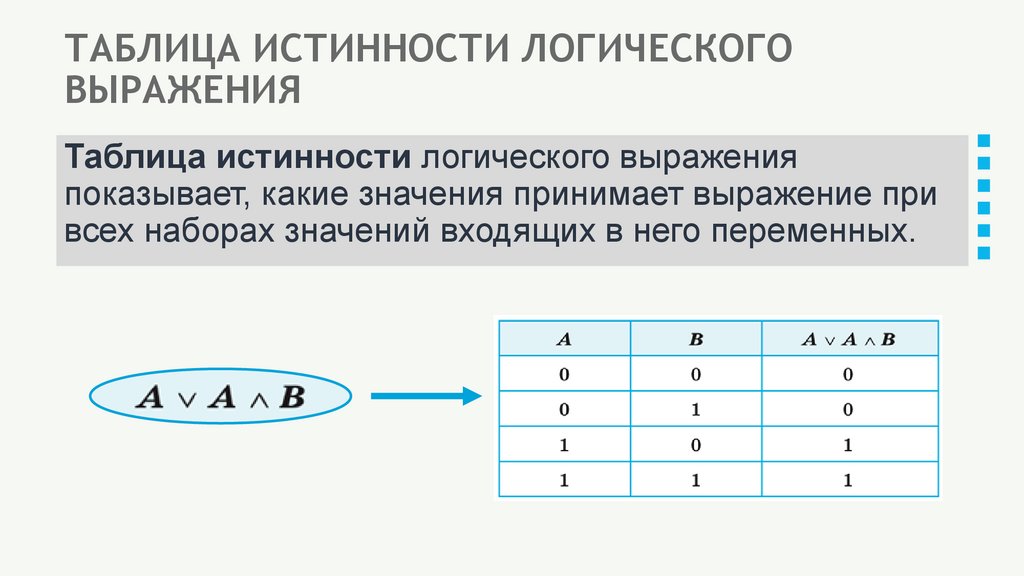
ТАБЛИЦА ИСТИННОСТИ ЛОГИЧЕСКОГОВЫРАЖЕНИЯ
Таблица истинности логического выражения
показывает, какие значения принимает выражение при
всех наборах значений входящих в него переменных.
4.
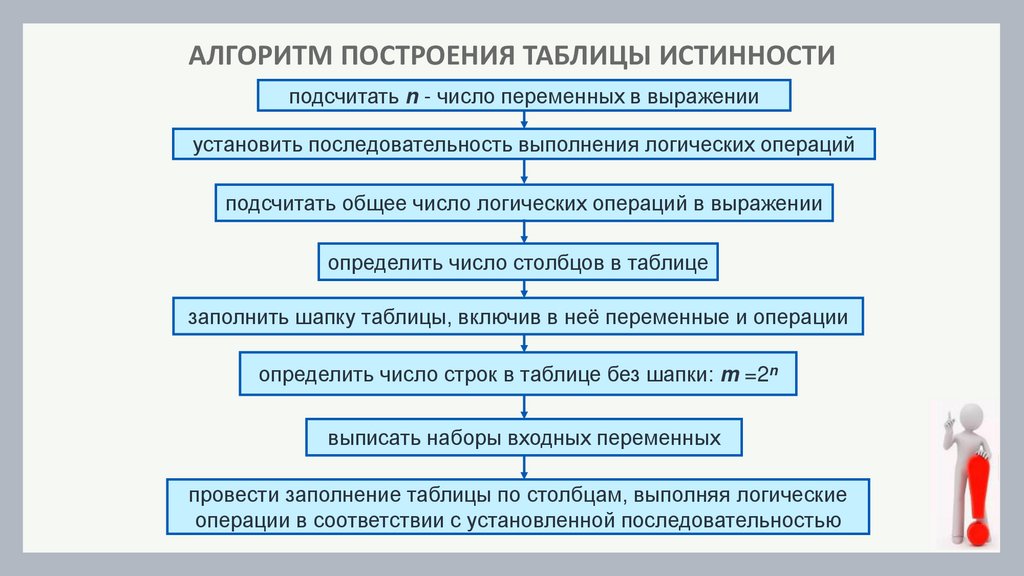
АЛГОРИТМ ПОСТРОЕНИЯ ТАБЛИЦЫ ИСТИННОСТИподсчитать n - число переменных в выражении
установить последовательность выполнения логических операций
подсчитать общее число логических операций в выражении
определить число столбцов в таблице
заполнить шапку таблицы, включив в неё переменные и операции
определить число строк в таблице без шапки: m =2n
выписать наборы входных переменных
провести заполнение таблицы по столбцам, выполняя логические
операции в соответствии с установленной последовательностью
5.
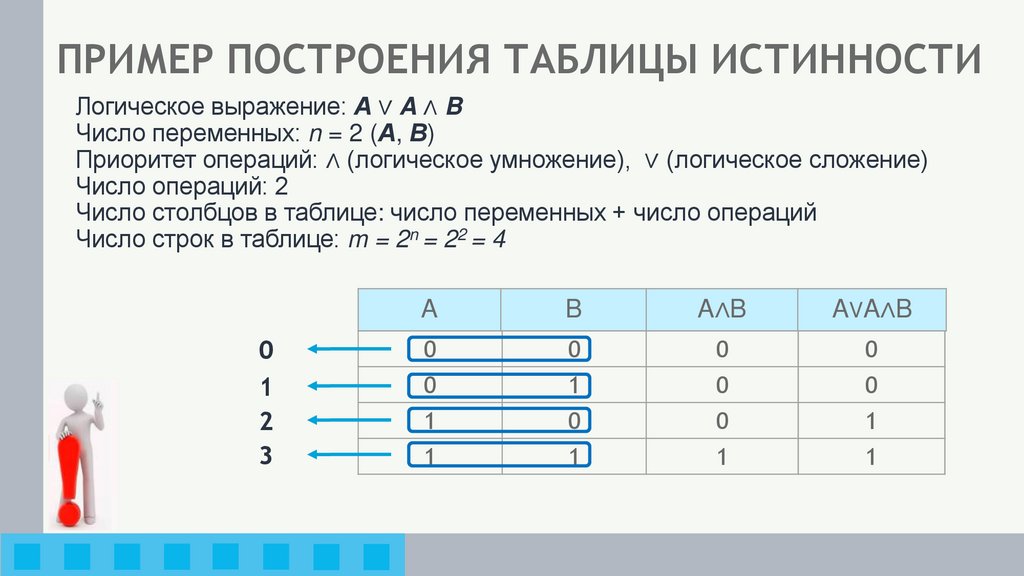
ПРИМЕР ПОСТРОЕНИЯ ТАБЛИЦЫ ИСТИННОСТИЛогическое выражение: А ∨ A ∧ B
Число переменных: n = 2 (А, В)
Приоритет операций: ∧ (логическое умножение), ∨ (логическое сложение)
Число операций: 2
Число столбцов в таблице: число переменных + число операций
Число строк в таблице: m = 2n = 22 = 4
0
1
2
3
A
B
A∧B
AVA∧B
0
0
0
0
0
1
0
0
1
0
0
1
1
1
1
1
6.
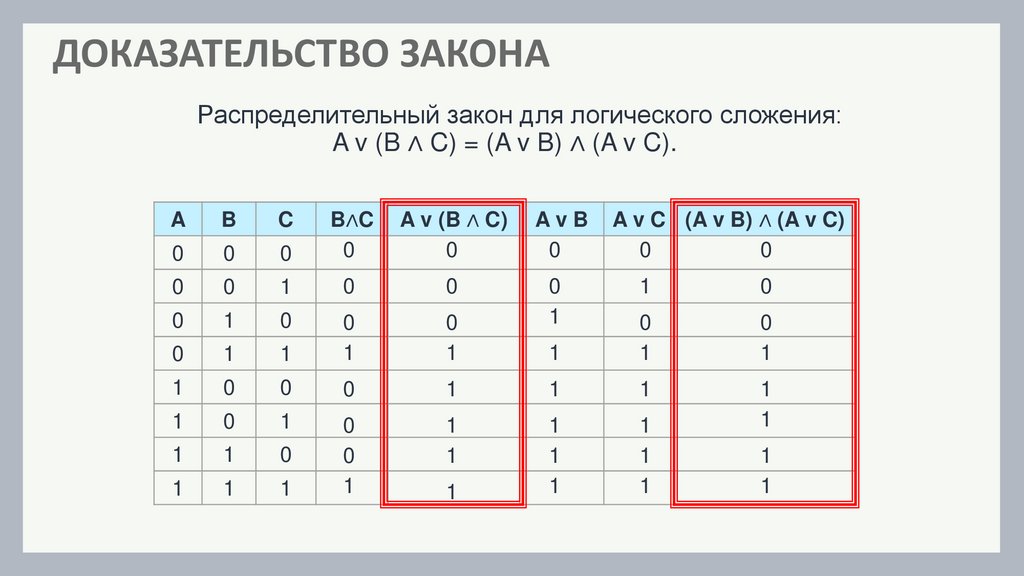
ДОКАЗАТЕЛЬСТВО ЗАКОНАРаспределительный закон для логического сложения:
A v (B ∧ C) = (A v B) ∧ (A v C).
0
B∧C
0
A v (B ∧ C)
0
AvB
0
0
1
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
0
0
0
1
0
1
1
1
0
1
1
1
0
0
1
A
B
C
0
0
0
A v C (A v B) ∧ (A v C)
0
0
1
0
1
0
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
7.
РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧЗадача. Коля, Вася и Серёжа гостили летом у бабушки. Однажды один из
мальчиков нечаянно разбил любимую бабушкину вазу.
На вопрос, кто разбил вазу, они дали такие ответы:
Серёжа: 1) Я не разбивал. 2) Вася не разбивал.
Вася: 3) Серёжа не разбивал. 4) Вазу разбил Коля.
Коля: 5) Я не разбивал. 6) Вазу разбил Серёжа.
Бабушка знала, что один из её внуков (правдивый), оба раза сказал правду;
второй (шутник) оба раза сказал неправду; третий (хитрец) один раз сказал
правду, а другой раз - неправду. Назовите имена правдивого, шутника и хитреца.
Кто из внуков разбил вазу?
8.
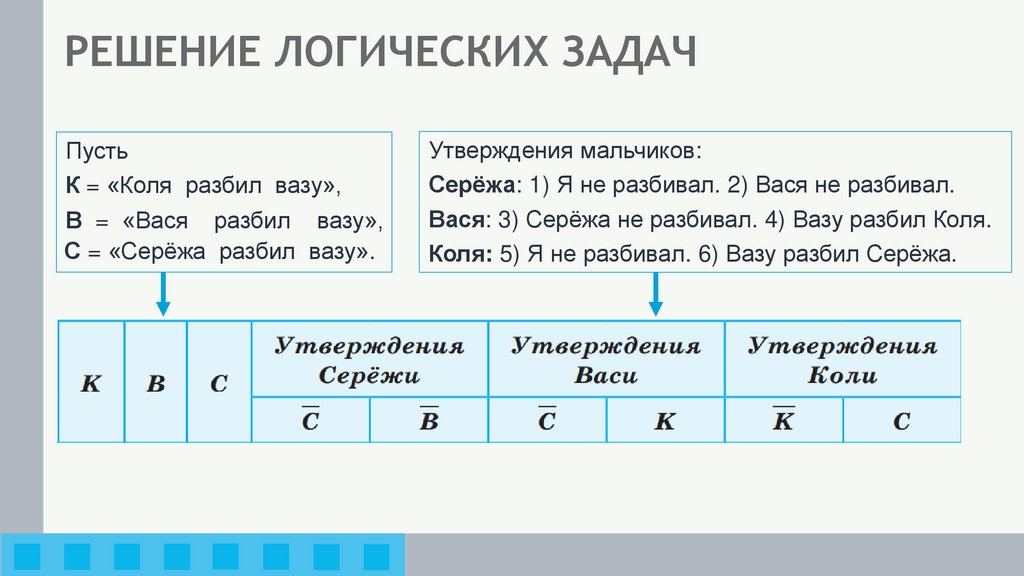
РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧПусть
К = «Коля разбил вазу»,
В = «Вася разбил вазу»,
С = «Серёжа разбил вазу».
Утверждения мальчиков:
Серёжа: 1) Я не разбивал. 2) Вася не разбивал.
Вася: 3) Серёжа не разбивал. 4) Вазу разбил Коля.
Коля: 5) Я не разбивал. 6) Вазу разбил Серёжа.
9.
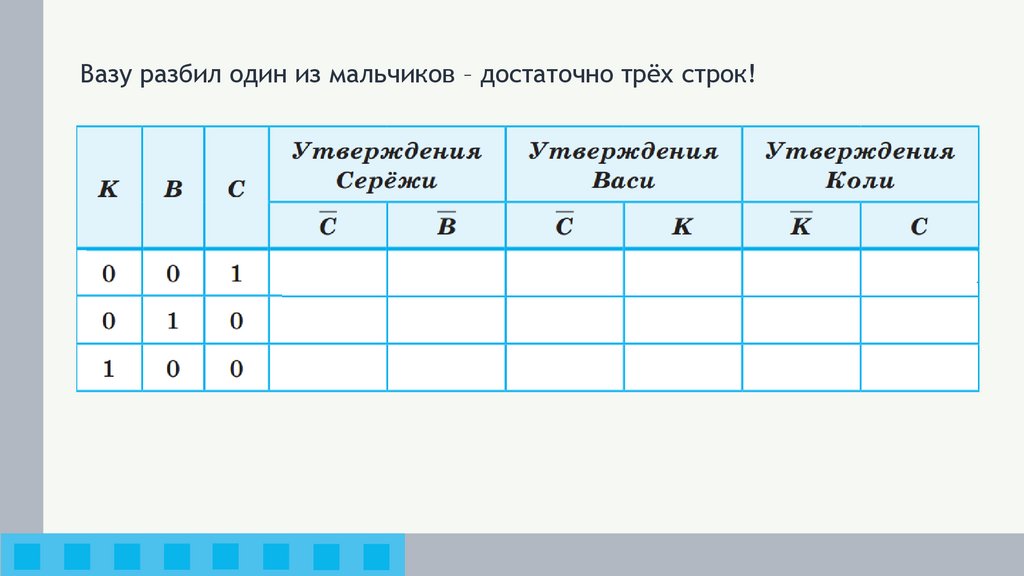
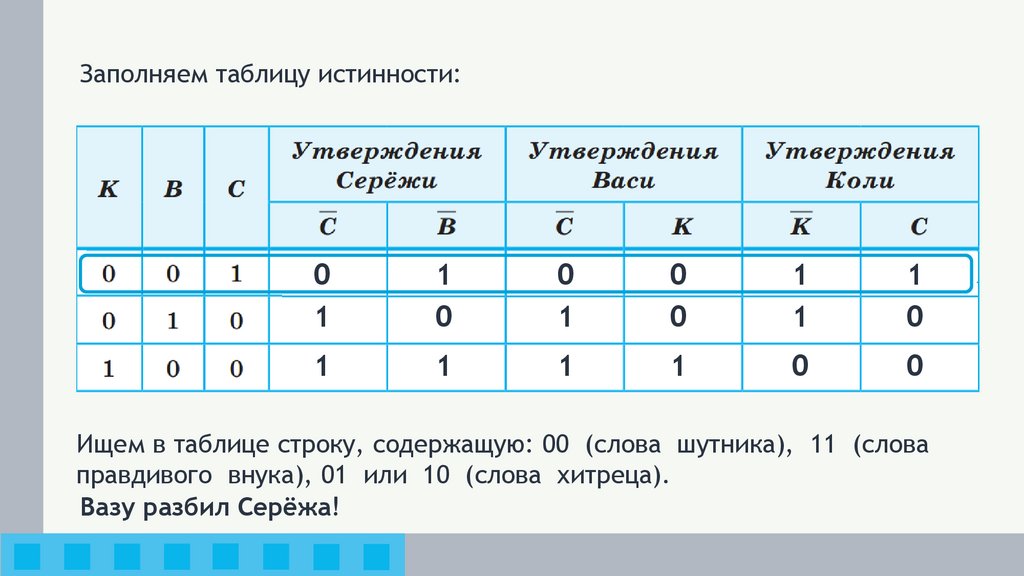
Вазу разбил один из мальчиков – достаточно трёх строк!10.
Заполняем таблицу истинности:0
1
1
0
0
1
0
0
1
1
1
0
1
1
1
1
0
0
Ищем в таблице строку, содержащую: 00 (слова шутника), 11 (слова
правдивого внука), 01 или 10 (слова хитреца).
Вазу разбил Серёжа!
11.
САМОЕ ГЛАВНОЕТаблица истинности логического выражения показывает,
какие значения принимает логическое выражение при всех
наборах значений входящих в него переменных.
Таблицу истинности можно построить для логического
выражения с любым числом переменных n; такая таблица
будет содержать 2n строк.
12.
ВОПРОСЫ И ЗАДАНИЯПостройте таблицы истинности для следующих логических
выражений:
а) В ∧ (А ∨ В)
б) А ∧ (В ∨ В)
в) В ∧ (А ∨ В ∨ С)
г) А ∧ В ∨ С
13.
ВОПРОСЫ И ЗАДАНИЯС помощью таблиц истинности докажите справедливость
следующих тождеств:
а) А ∨ В = A ∧ B
б) А ∧ В = A ∨ B
14.
ВОПРОСЫ И ЗАДАНИЯСколько строк содержат таблицы истинности для следующих
выражений? Для каких наборов значений переменных эти
выражения истинны?
а) А ∧ В ∧ С;
б) А ∧ В ∧ С ∧ D;
в) А ∨ В ∨ С;
г) А ∨ В ∨ С ∨ D.
Ответьте на вопросы, не прибегая к заполнению таблиц
истинности.
15.
ВОПРОСЫ И ЗАДАНИЯВ школьной олимпиаде по информатике приняли участие три
ученика 8 класса: Александр, Иван и Мария. Перед
олимпиадой их друзья высказали три предположения.
1. Александр сможет пройти на городской тур олимпиады или Иван не
сможет пройти на городской тур олимпиады.
2. Иван сможет пройти на городской тур олимпиады.
3. Неверно, что Мария и Александр смогут пройти на городской тур
олимпиады.
Кто из ребят прошёл на городской этап олимпиады, если все
предположения оказались истинными высказываниями?
16.
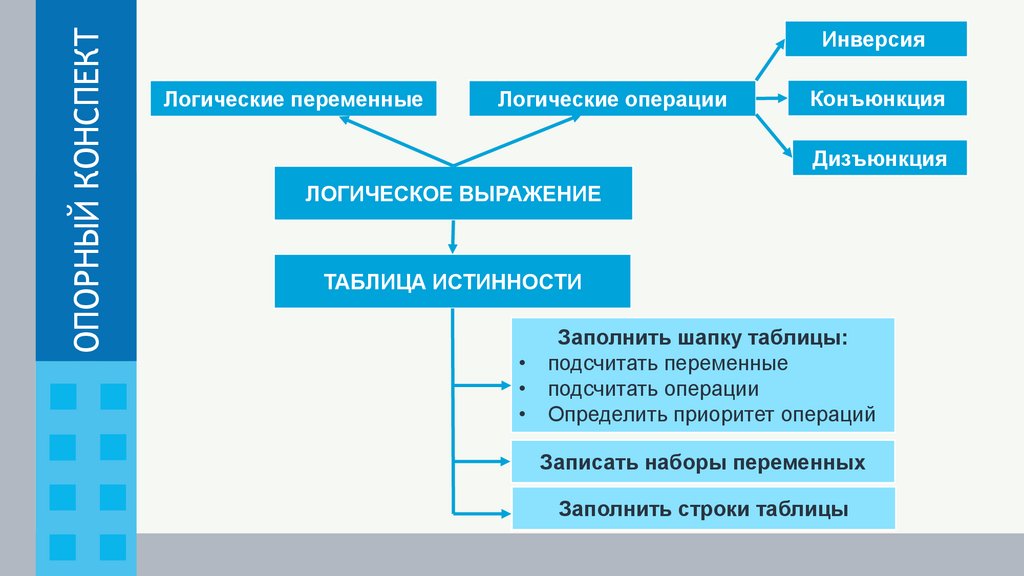
ОПОРНЫЙ КОНСПЕКТИнверсия
Логические переменные
Логические операции
Конъюнкция
Дизъюнкция
ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ
ТАБЛИЦА ИСТИННОСТИ
Заполнить шапку таблицы:
• подсчитать переменные
• подсчитать операции
• Определить приоритет операций
Записать наборы переменных
Заполнить строки таблицы








 informatics
informatics