Двоичные коды

1.

Двоичные коды
Доцент каф. ВТ, к.т.н Медведев М.С.

2.

Двоичные коды
Прямой, обратный и дополнительный коды
двоичного числа - способы представления двоичных
чисел с фиксированной запятой в компьютерной
(микроконтроллерной) арифметике, предназначенные
для записи отрицательных и неотрицательных чисел
2

3.

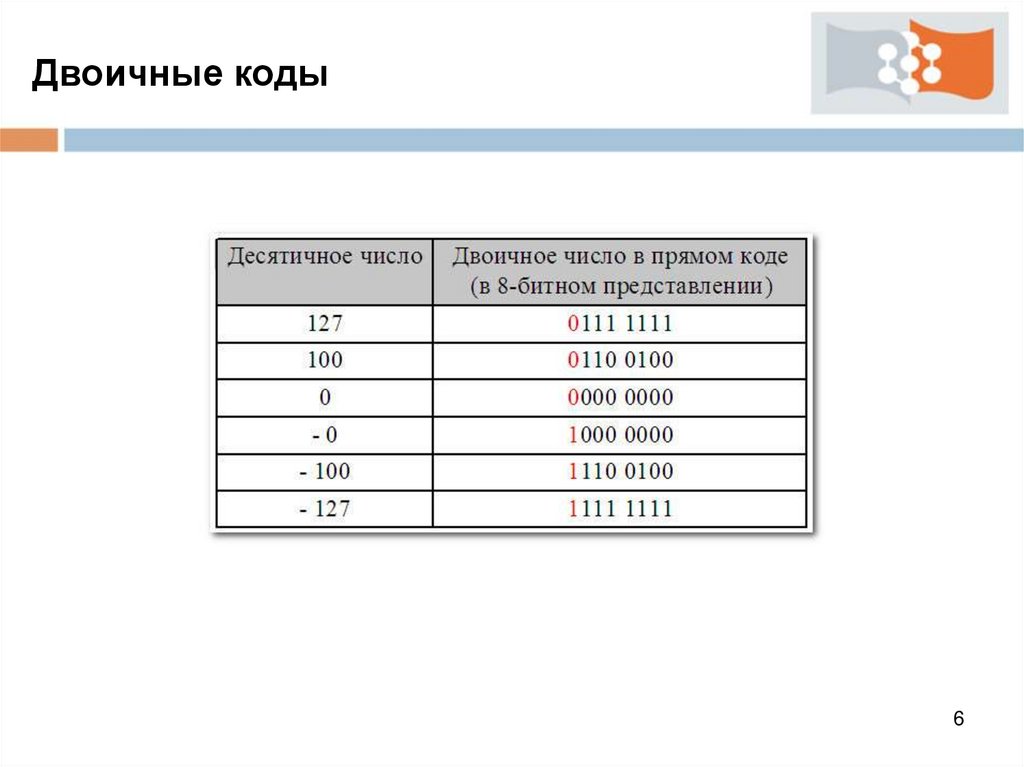
Двоичные коды
Прямой код - способ представления двоичных чисел
с фиксированной запятой.
Прямой код используется в двух вариантах.
В первом (основной) - для записи только
неотрицательных чисел:
3

4.

Двоичные коды
Второй вариант - для записи как положительных, так
и отрицательных чисел.
В этом случае старший бит объявляется знаковым
разрядом (знаковым битом).
При этом, если:
- знаковый разряд равен 0, то число положительное
- знаковый разряд равен 1, то число отрицательное
4

5.

Двоичные коды
В этом случае диапазон десятичных чисел, которые
можно записать в прямом коде составляет от - 127 до
+127
5

6.

Двоичные коды
6

7.

Двоичные коды
Прямой код используется главным образом для
представления неотрицательных чисел.
Использование прямого кода для представления
отрицательных чисел является неэффективным очень сложно реализовать арифметические
операции.
В прямом коде два представления нуля положительный ноль и отрицательный ноль.
7

8.

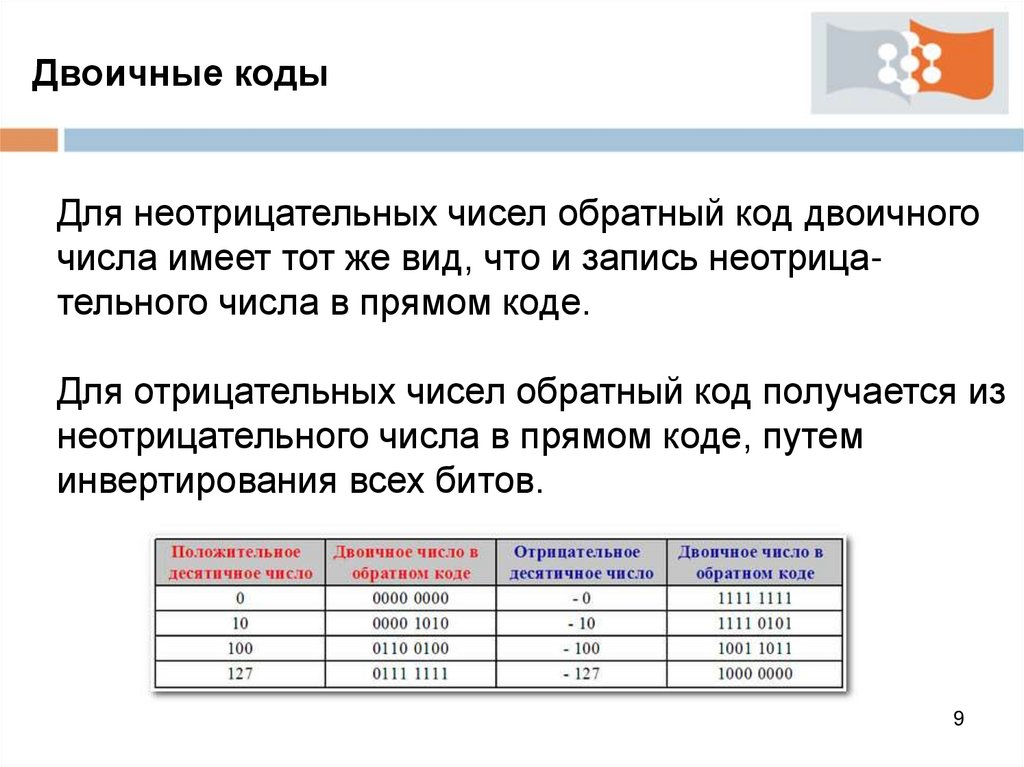
Двоичные коды
Обратный код - метод вычислительной математики,
позволяющий вычесть одно число из другого,
используя только операцию сложения.
Обратный двоичный код положительного числа состоит
из одноразрядного кода знака (битового знака) двоичной цифры 0, за которым следует значение числа.
Обратный двоичный код отрицательного числа состоит
из одноразрядного кода знака (битового знака) двоичной цифры 1, за которым следует инвертированное
значение положительного числа.
8

9.

Двоичные коды
Для неотрицательных чисел обратный код двоичного
числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из
неотрицательного числа в прямом коде, путем
инвертирования всех битов.
9

10.

Двоичные коды
Арифметические операции с отрицательными
числами в обратном коде:
1-й пример (для положительного результата)
Дано два числа:
100 = 0110 0100
-25 = - 0001 1001
Необходимо их сложить:
100 + (-25) = 100 - 25 = 75
10

11.

Двоичные коды
1-й этап
Переводим число -25 в двоичное число в обратном
коде:
25 = 0001 1001
-25= 1110 0110
складываем числа:
0110 0100 (100) + 1110 0110 (-25) = 1 0100
1010, отбрасываем старшую 1 (9-й разряд - переполнение) = 0100 1010
11

12.

Двоичные коды
2-й этап
Отброшенную в результате старшую единицу
прибавляем к результату:
0100 1010 + 1 = 0100 1011
знаковый бит = 0, значит число положительное, что
равно 75 в десятичной системе
12

13.

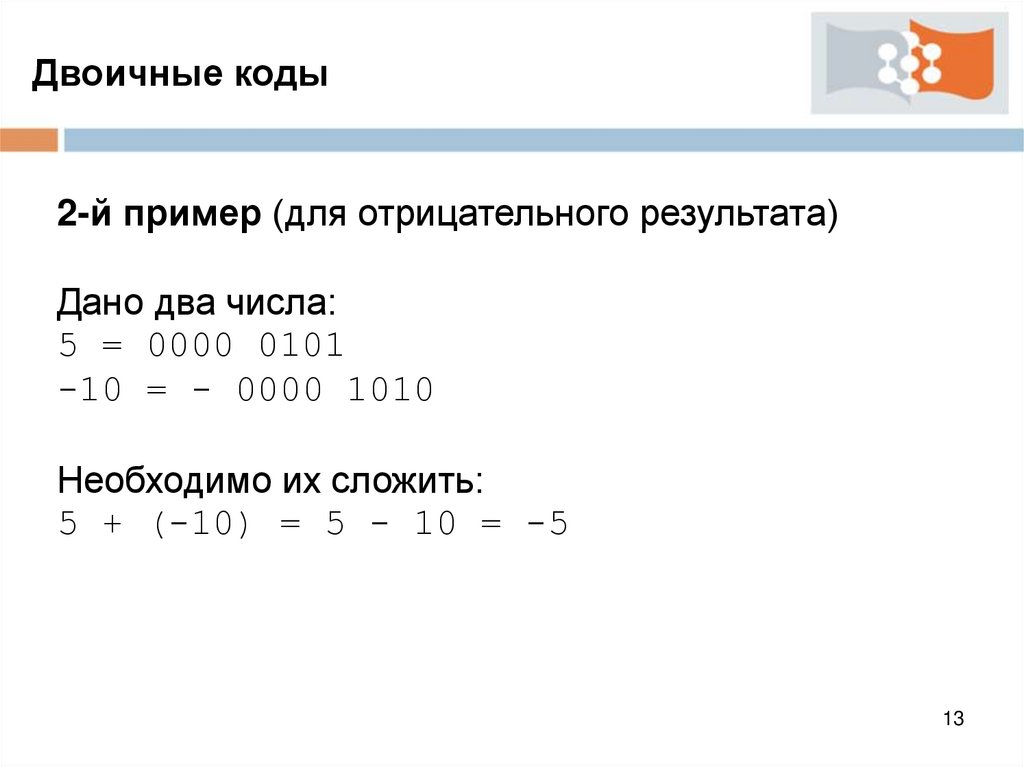
Двоичные коды
2-й пример (для отрицательного результата)
Дано два числа:
5 = 0000 0101
-10 = - 0000 1010
Необходимо их сложить:
5 + (-10) = 5 - 10 = -5
13

14.

Двоичные коды
1-й этап
Переводим число -10 в двоичное число в обратном
коде:
10 = 0000 1010
-10= 1111 0101
складываем числа:
0000 0101 (5) + 1111 0101 (-10) =
1111 1010
знаковый бит =1, значит число отрицательное
14

15.

Двоичные коды
2-й этап
Раз результат получился отрицательный, значит число
представлено в обратном коде.
Переводим результат в прямой код (путем
инвертирования значения, знаковый бит не трогаем):
1111 1010 -> 1000 0101
Проверяем:
1000 0101 = - 0000 0101 = -5
15

16.

Двоичные коды
Обратный код решает проблему сложения и
вычитания чисел с различными знаками, но и имеет
свои недостатки:
- арифметические операции проводятся в два этапа;
- как и в прямом коде два представления нуля положительный и отрицательный.
16

17.

Двоичные коды
Дополнительный код - наиболее распространенный
способ представления отрицательных чисел.
Он позволяет заменить операцию вычитания на
операцию сложения и сделать операции сложения и
вычитания одинаковыми для знаковых и беззнаковых
чисел.
17

18.

Двоичные коды
Выполнение арифметических операций над числами
с разными знаками представляется для аппаратной
части довольно сложной процедурой. В этом случае
нужно определить большее по модулю число,
произвести вычитание и присвоить разности знак
большего по модулю числа.
Применение
дополнительного
кода
позволяет
выполнить операцию алгебраического суммирования
и вычитания на обычном сумматоре. При этом не
требуется определения модуля и знака числа.
18

19.

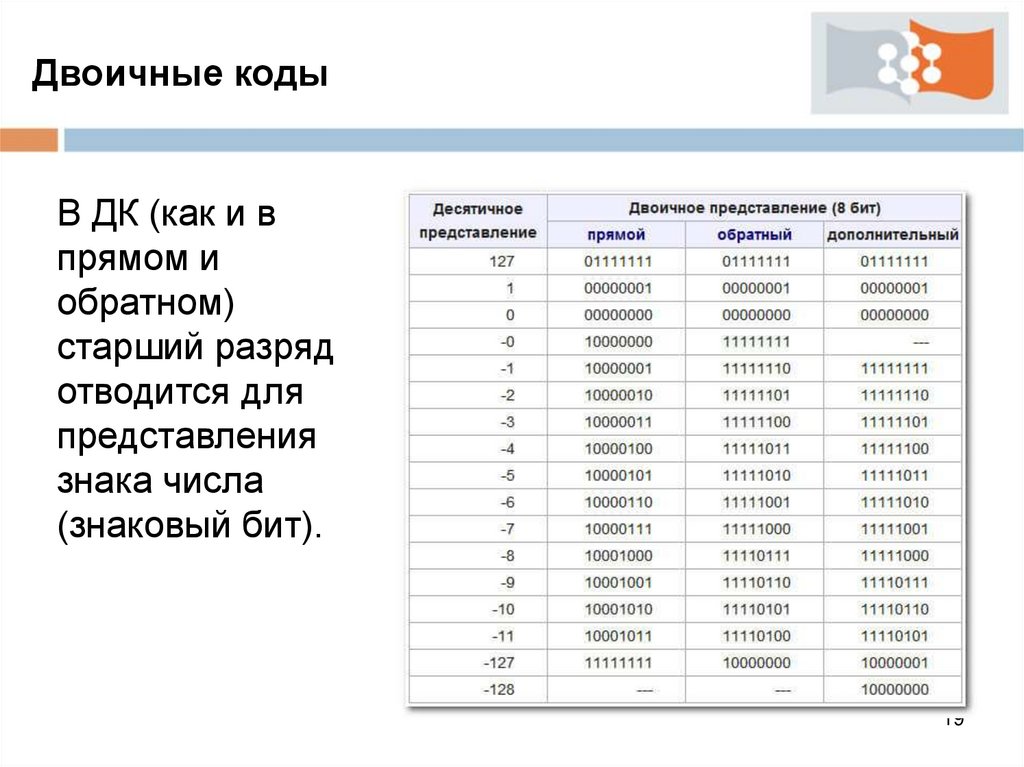
Двоичные коды
В ДК (как и в
прямом и
обратном)
старший разряд
отводится для
представления
знака числа
(знаковый бит).
19

20.

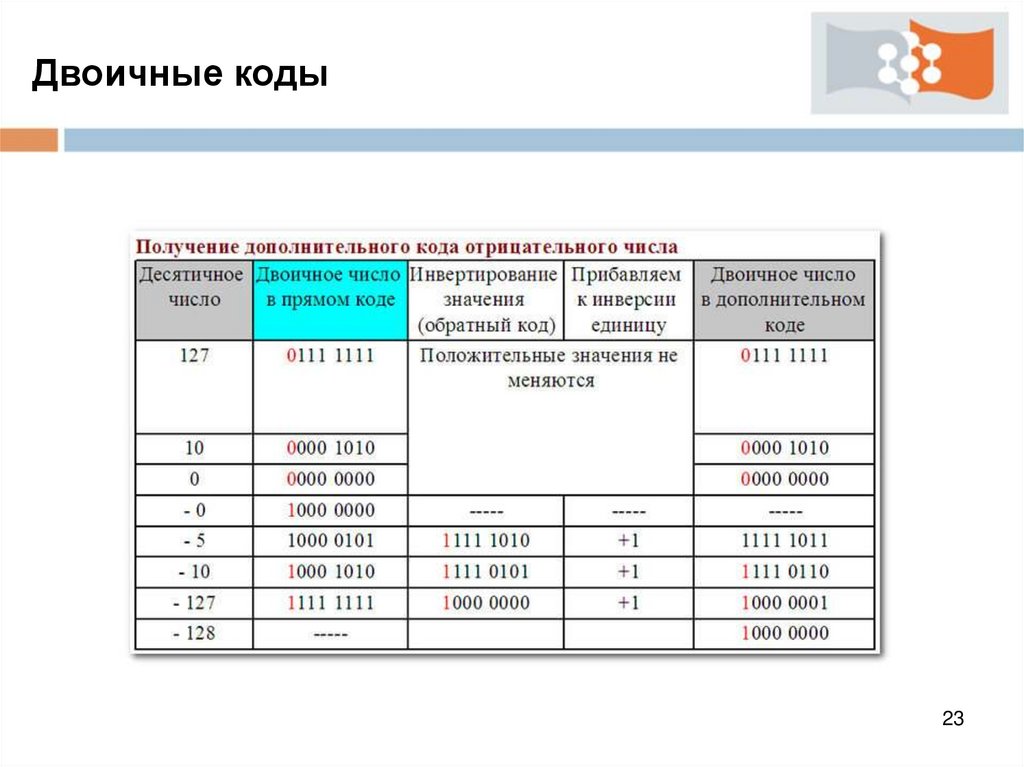
Двоичные коды
Дополнительный код отрицательного числа можно
получить двумя способами.
1-й способ:
- инвертируем значение отрицательного числа,
записанного в прямом коде (знаковый бит не трогаем)
- к полученной инверсии прибавляем 1
20

21.

Двоичные коды
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 0000 1010 ----> -10 = 1000 1010
Инвертируем значение (получаем обратный код):
1000 1010 ----> 1111 0101
К полученной инверсии прибавляем 1:
1111 0101 + 1 = 1111 0110 - десятичное число
- 10 в дополнительном коде
21

22.

Двоичные коды
2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить
отрицательное число (-10) в дополнительном
двоичном коде.
Переводим 10 в двоичное число:
10 = 0000 1010
Вычитаем из нуля:
0 - 0000 1010 = 1111 0110 - десятичное число
-10 в дополнительном коде
22

23.

Двоичные коды
23

24.

Двоичные коды
Арифметические операции с отрицательными
числами в дополнительном коде:
Необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что
соответствует числу -5 в дополнительном коде
24

25.

Двоичные коды
Вывод:
1. Для арифметических операций сложения и
вычитания положительных двоичных чисел наиболее
подходит применение прямого кода
2. Для арифметических операций сложения и
вычитания отрицательных двоичных чисел наиболее
подходит применение дополнительного кода
25

26.

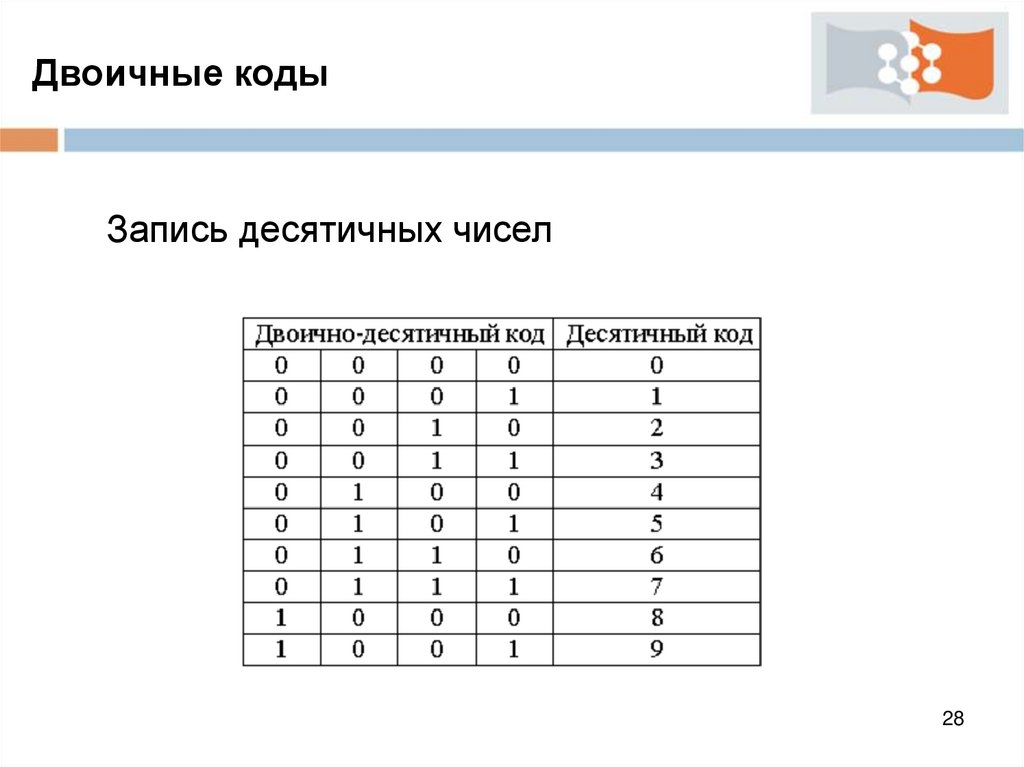
Двоичные коды
Запись десятичных чисел
Иногда удобно хранить числа в памяти процессора в
десятичном виде (например, для вывода на дисплей).
Для записи таких чисел используются двоичнодесятичные коды.
Для записи одного десятичного разряда используется
четыре двоичных бита. Эти четыре бита называются
тетрадой.
26

27.

Двоичные коды
Запись десятичных чисел
При помощи четырех бит можно закодировать
шестнадцать цифр.
Лишние комбинации в двоично-десятичном коде
являются запрещенными.
27

28.

Двоичные коды
Запись десятичных чисел
28

29.

Двоичные коды
Запишем пример двоично-десятичного кода:
1258 = 0001 0010 0101 1000
589 = 0000 0101 1000 1001
29

30.

Двоичные коды
Достаточно часто в памяти процессора для хранения
одной десятичной цифры выделяется одна ячейка
памяти (восьми, шестнадцати или
тридцатидвухразрядная).
Это делается для повышения скорости работы
программы.
Такой способ записи десятичного числа называется
упакованной формой двоично-десятичного числа.
30

31.

Двоичные коды
Суммирование двоично-десятичных чисел.
Суммирование двоично-десяичных чисел можно
производить по правилам обычной двоичной
арифметики, а затем производить двоичнодесятичную коррекцию.
Двоично-десятичная коррекция заключается в
проверке каждой тетрады на допустимые коды. Если
в какой либо тетраде обнаруживается запрещенная
комбинация , то это говорит о переполнении. В этом
случае необходимо произвести двоично-десятичную
коррекцию.
31

32.

Двоичные коды
Суммирование двоично-десятичных чисел.
Двоично-десятичная коррекция заключается в
дополнительном суммировании числа шесть 0110
(число запрещенных комбинаций) с тетрадой, в
которой произошло переполнение или произошел
перенос в старшую тетраду.
32

33.

Двоичные коды
Суммирование двоично-десятичных чисел.
33

34.

Двоичные коды
Вычитание двоично-десятичных чисел производится
по правилам двоичного вычитания с вводимой в
необходимых случаях коррекцией результата.
Такая коррекция заключается в вычитании кода 0110
из тех тетрад результата, которые использовали
межтетрадный заем.
34