Similar presentations:
ДС_Л.3, 4_Локальная бифуркация_ИЗО
1. Локальные бифуркации в одномерных динамических системах
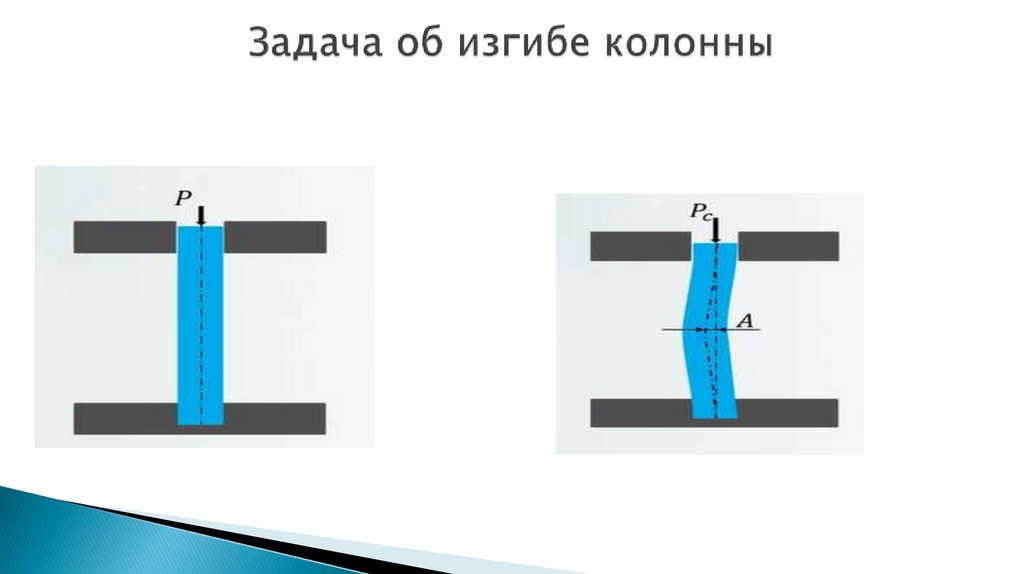
2. Задача об изгибе колонны
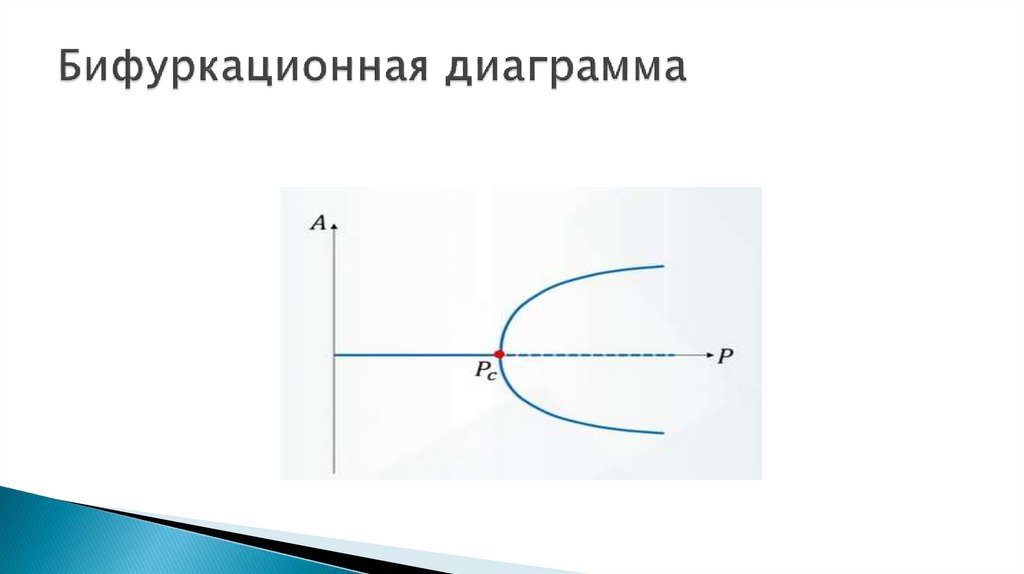
3. Бифуркационная диаграмма
4. Основные понятия теории бифуркации
Существуют два основных класса задач, которые решаютсяв рамках качественной теории динамических систем:
1) изучение поведения систем при фиксированных
значениях параметрах (построение фазового портрета);
2)качественные изменения в системе при изменении
значений параметров, т. е. бифуркация.
Бифуркация – это качественная перестройка фазового
портрета динамической системы при малых изменениях
ее параметров (бифуркационных параметров).
5. Основные понятия теории бифуркации
Значения параметров, при которых происходит бифуркация –это бифуркационные значения или точки бифуркации системы).
В динамической системе может быть как один бифуркационный
параметр, так и несколько.
Минимальным количеством бифуркационных параметров и
определяется коразмерность бифуркации.
Бифуркационная диаграмма – изображение смены всех
возможных динамических режимов системы при изменении
значения бифуркационного параметра.
6. Основные понятия теории бифуркации
Выделяют два класса динамических систем.Грубые динамические системы: при малом изменении
параметров динамической системы или правой части
динамического уравнения вид фазового портрета
качественно не изменяется.
В таких системах никаких бифуркаций не происходит.
7. Основные понятия теории бифуркации
Негрубые динамические системы: при малом изменениипараметров динамической системы или правой части
динамического уравнения качественно изменяется вид
фазового портрета.
Из одного равновесия рождается другое или несколько.
Или система находилась в состоянии неустойчивого
равновесия, а в результате бифуркации она переходит в
состояние устойчивого равновесия.
8. Основные понятия теории бифуркации
Выделяют два класса бифуркации:локальная бифуркация или бифуркация равновесия;
глобальная бифуркация.
Рассмотрим первый класс – бифуркацию равновесия.
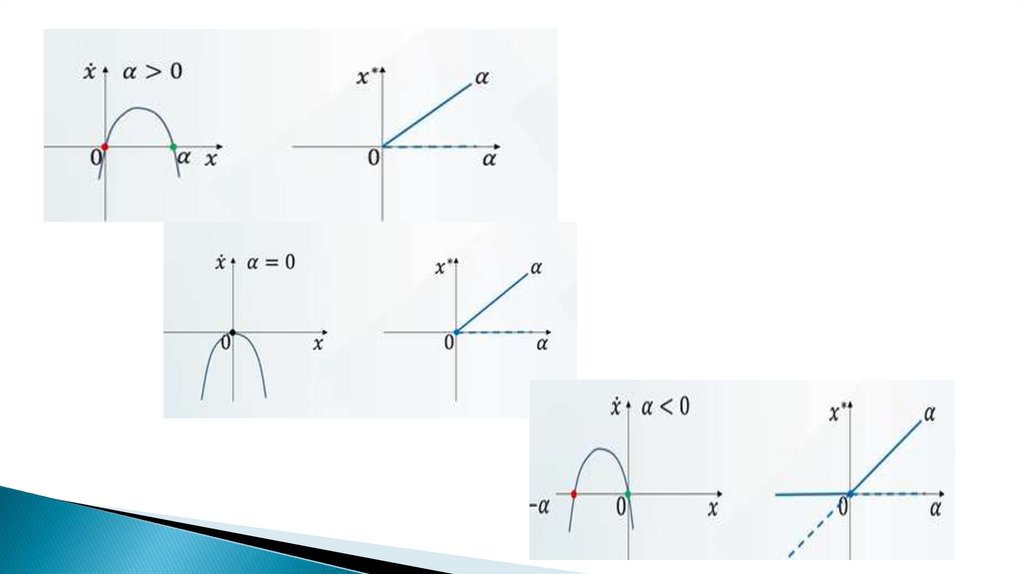
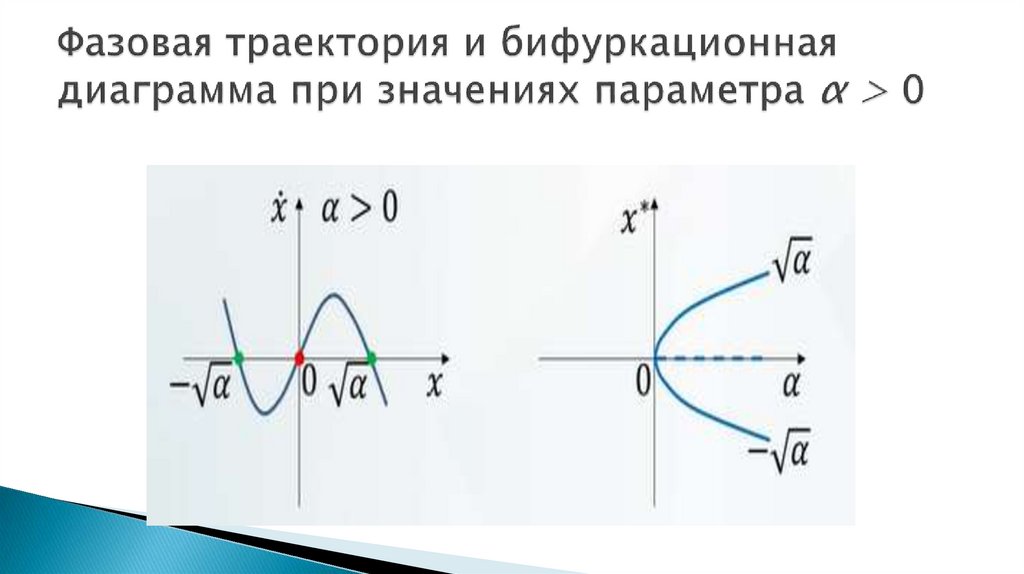
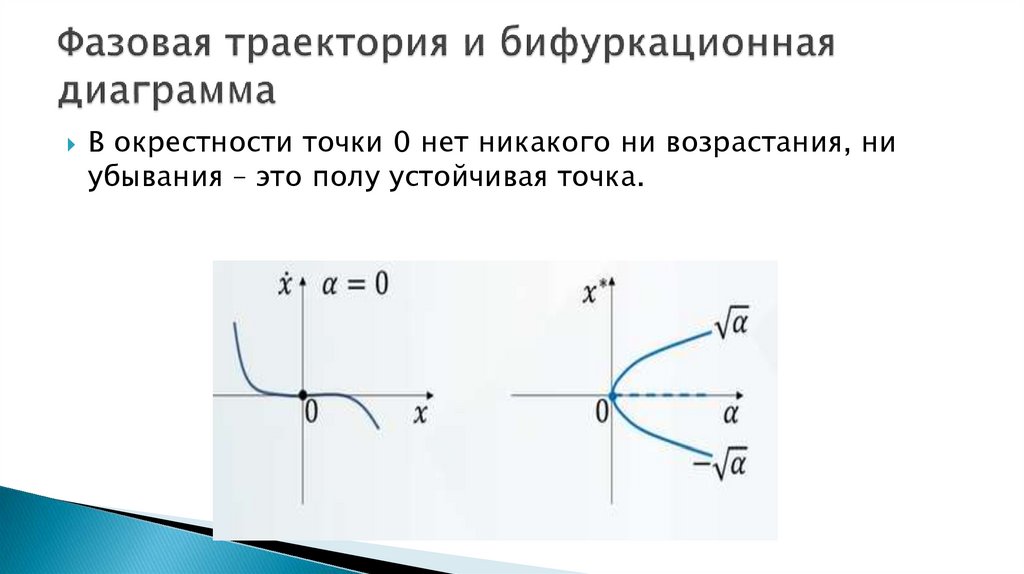
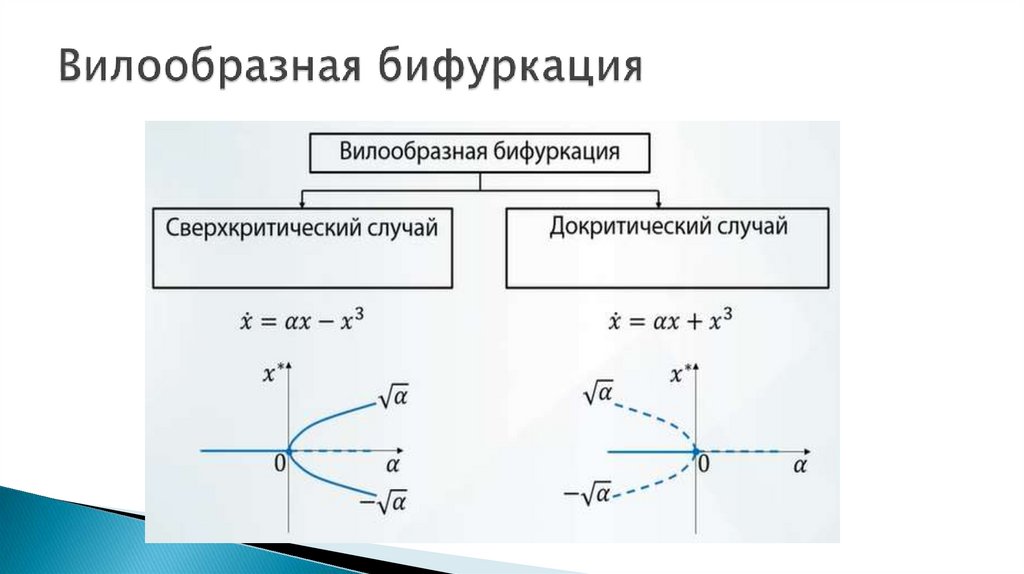
9. Седло-узловая бифуркация
Бифуркация равновесий – это бифуркации в динамическойсистеме, в которых изменяется: число равновесных точек и
/ или их устойчивость.
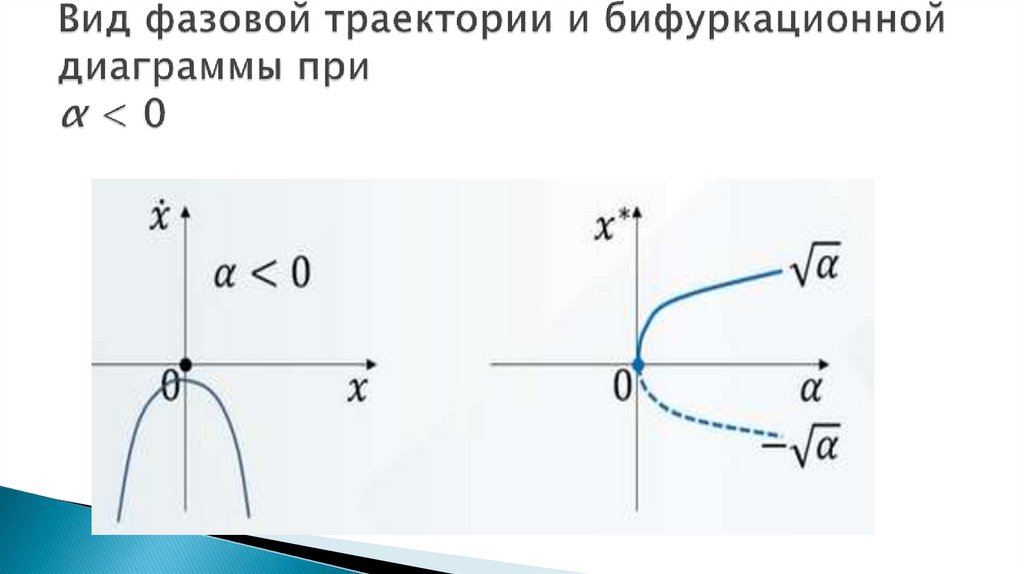
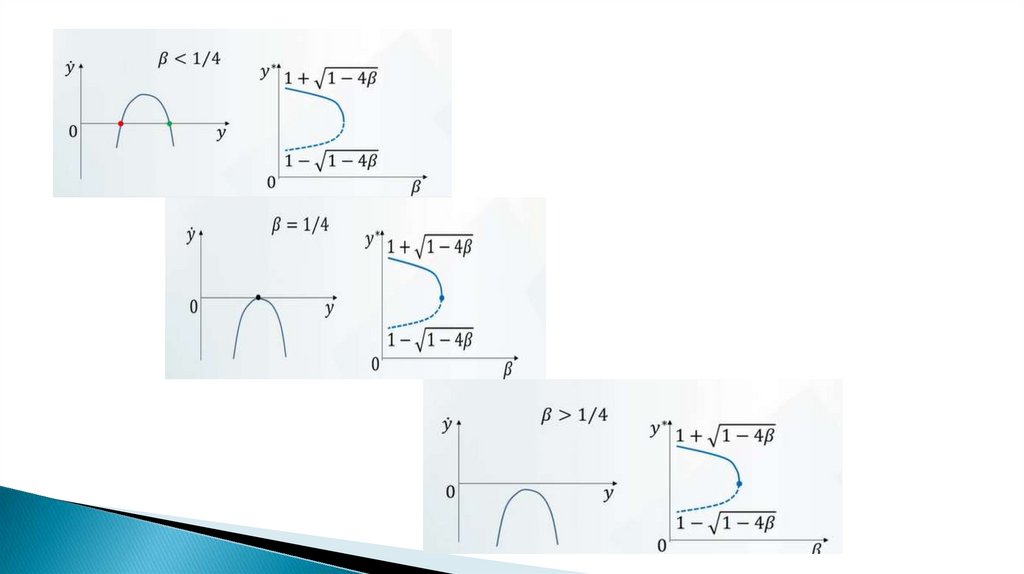
Нормальная форма седло-узловая бифуркация:
ẋ = α – х2,
α – параметр бифуркации.