Urok_34_Skalyarnoe_proizvedenie_vektorov_2

1. Скалярное произведение векторов, его применение для нахождения длин и углов.

ПОДГОТОВИЛА:
УЧИТЕЛЬ МАТЕМАТИКИ
ГБОУ «ШКОЛА № 42 Г.О.ГОРЛОВКА»
РЫБИНА М.В.

2. Скалярное произведение

Скалярным произведением двух векторов a и b будет скалярная
величина, равная произведению модулей этих векторов, умноженная
на косинус угла между ними:

3.

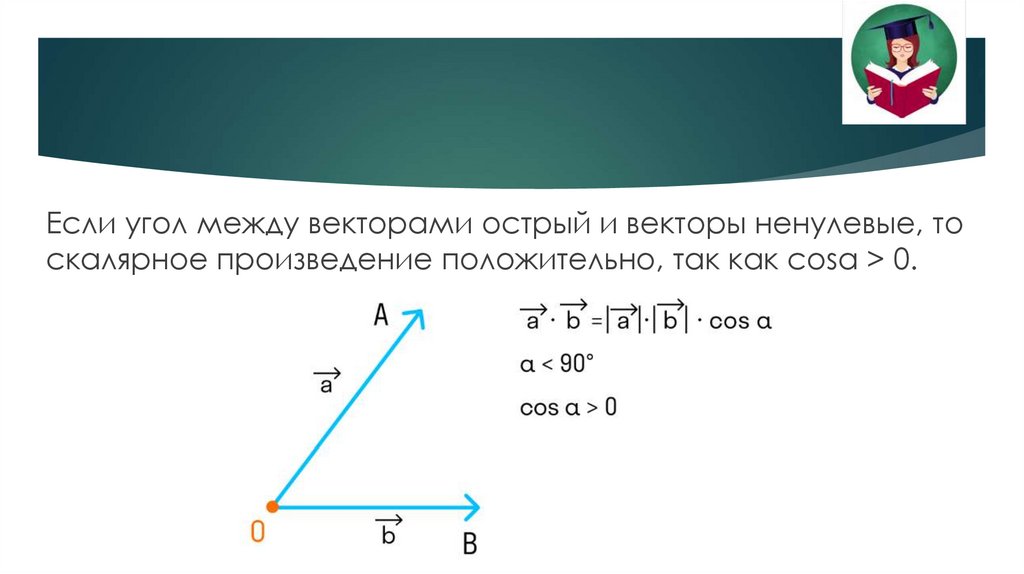
Если угол между векторами острый и векторы ненулевые, то
скалярное произведение положительно, так как cosα > 0.

4.

Если угол между векторами тупой и векторы
ненулевые,
то
скалярное
произведение
отрицательно, так как cosα < 0.

5.

Если угол между векторами прямой,
произведение равно 0, так как cosα = 0.
то
скалярное

6. Скалярное произведение векторов, заданных координатами

7. Задание 1

-10

8. Задание 2

0

9. Задание 3

10. Задание 4

Найдите косинус угла между
1 1
векторами m
ഥ {1; 7} и nത {− ; }.
2
2

11. Задание 5

При каком значении х векторы m
ഥ { х; -1 }
и nഥ {3;2 } векторы перпендикулярны?

12. Задание 6

Найдите угол М в треугольнике с вершинами
М(2; 4 3), N(– 2; 0), К(2; 0).

13. Задание 7

Треугольник MNP задан координатами вершин
М(2; 2 3), N(0; 0), P(3; 3). Найдите углы
треугольника.

14. Домашнее задание

1. Найдите косинус угла между векторами c
ത {1; 0 } и dത {0;
2. Найдите угол А в треугольнике с вершинами А(1; 2
В(– 1; 0), С(1, 0).
3),
1
}.
2

15. Использованные источники

https://resh.edu.ru/subject/lesson/2039/main/
https://www.yaklass.ru/p/geometria/9-klass/sootnosheniia-mezhdu-storonamii-uglami-treugolnika-skaliarnoe-proizvedeni_-9222/skaliarnoe-proizvedenievektorov-svoistva-9526/re-4c246f69-ab7f-4efb-8d1f-5c49e95d1c06
https://skysmart.ru/articles/mathematic/skalyarnoe-proizvedenie-vektorov
https://www.evkova.org/vektor