Обучающий электронный ресурс

1.

Открытый банк
заданий
http://www.mathege.ru:8080/or/ege/ShowProblems?posMask=512
470 заданий, прототипов 13
10
Обучающий электронный ресурс
(с эффектами анимации)

2.

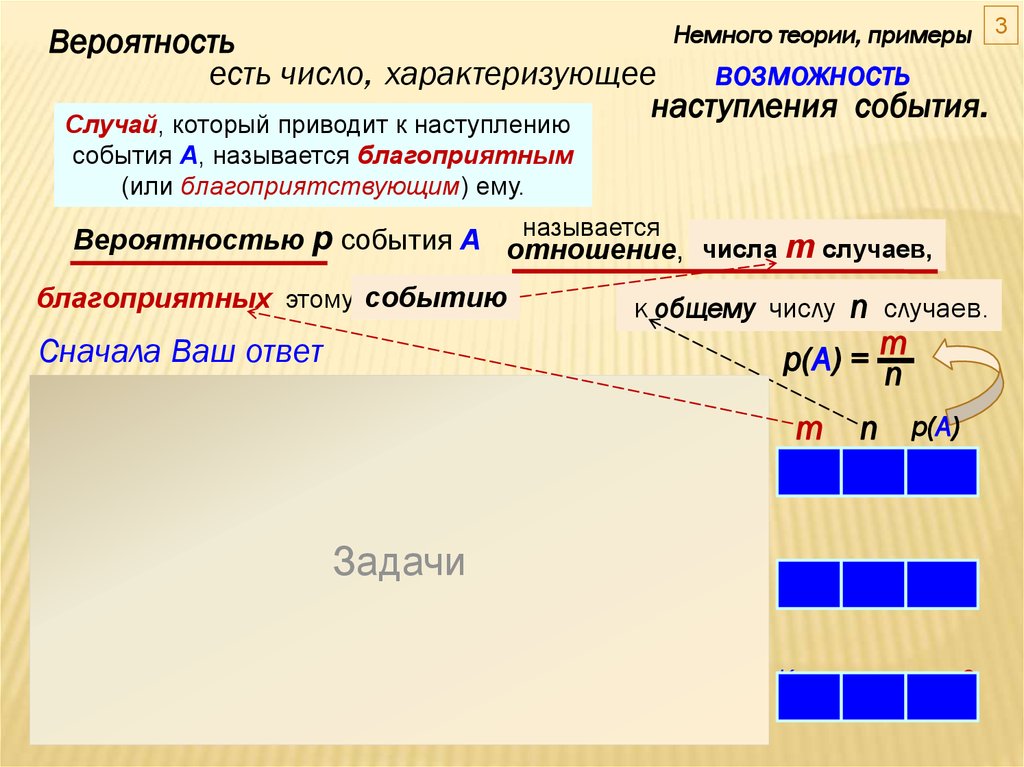
Немного теории, примеры
Вероятность
есть число, характеризующее
возможность
наступления события.
Случай, который приводит к наступлению
события А, называется благоприятным
(или благоприятствующим) ему.
называется
Вероятностью p события А отношение,
числа m случаев,
благоприятных этому событию
испытанию
искомому
варианту
событию
случаю
к общему числу n случаев.
Сначала Ваш ответ
1.Игральный кубик (кость) бросили один раз. Найдите
вероятность того, что выпавшее количество очков
чётное.
2. На экзамен по математике всего 20 билетов, в 13
из них встречается вопрос по производной. Найдите
вероятность того, чтоЗадачи
в выбранном билете не будет
вопроса по производной.
m
p(A) = ―
n
m n p(A)
3 6 0,5
7
20 0,35
Событие
(А) {выбор
№ карточки}
3.На карточках
написаны
номера от 4 до 35. Какова
трёх
Нет карточек
1, случайно
2, 3 → Всего
исходов
(n) 32 Как рассуждали ?
вероятность
того,№
что
выбранная
карточка
будет
иметь
номерисход
делящийся
на15,
5 (округлите
до →
сотых)
7 32 0,22
Номера,
Благоприятный
делящиеся
на 5 5,10,
m=7
20, 25,30, 35
3

3.

В10 Консультация
4
4.Фабрика выпускает сумки. В среднем на 180 качественных сумок
приходится две сумки со скрытыми дефектами. Найдите
вероятность того, что купленная сумка окажется качественной.
Результат округлите до сотых.
Событие (А){выпуск сумок}
По условию
Находим отношение {качественные}
количества
в среднем выпускают
{качественные} + {брак}
качественных - m
на 180 качественных
180
2 с дефектами
к общему
≈ 0,98901… 0,99
182
количеству- n
То есть -180
всего
+ 2 = 182
Округляем до сотых
Проследите
Закрепляем Сначала Ваш ответ
5.В среднем из 500 садовых насосов, поступивших в продажу,
4 подтекают. Найдите вероятность того, что один случайно
выбранный для контроля насос не подтекает.
благоприятных
Событие (А)-{выбор насоса} не
подтекают-m:
ответ
0,992
ИЗ (n=500) 4 подтекают
500 – 4 = 496
Проверить решение
Вероятность p( A)= 496 : 500 = 0,992
Сравните
условия
Вывод

4.

Закрепление
Сначала Ваш ответ.
5
6.В чемпионате по гимнастике участвуют 50 спортсменок: 19 из
России, 14 из США, остальные — из Китая. Порядок, в котором
выступают
гимнастки,
определяется
жребием.
Найдите
вероятность того, что спортсменка, выступающая первой,
окажется из Китая.
ответ
0,34
= 50
Событие (А) {выбор гимнастки Китая} nВсего
Спортсменок России и США
19+14 = 33
Проверить
решение
№6
Благоприятных
спортсменок
исходов
m Китая
50-33 = 17
Вероятность, что первой выступит
17 : 50
7. На семинар приехали 3 учёных из Норвегии, 3 из России и 4 из
Испании. Порядок докладов определяется жеребьёвкой. Найдите
вероятность того, что восьмым окажется доклад учёного из России.
Событие (А) {выбор докладчика из России}
Всего учёных (докладов - n)
3+3+4 = 10
ответ
0,3
благоприятных
(m) 3
Событию (А)-Проверить
решение исходов
№7
Вероятность выступления р(А)
3:10
(неважно, под каким номером выступление)

5.

6
Сначала Ваш ответ.
8. Научная конференция проводится в 5 дней. Всего запланировано 75
докладов – первые три дня по 15 докладов, остальные распределены
поровну между четвёртым и пятым днями. Порядок докладов определён
жеребьёвкой. Какова вероятность, что доклад профессора М. окажется
запланированным на последний день конференции ?
0,2
ответ
Событие (А)
прядок докладов
5-й день р(А)
{доклад
М.
на
последний
день}
определяется из
докладов
Решение задачи № 8
15
―
75 докладов - это n
15
благоприятствующих исходов
75
9. Перед началом первого тура чемпионата по бадминтону участников
разбивают на игровые пары случайным образом с помощью жребия.
Всего в чемпионате участвует 26 бадминтонистов, среди которых 10
участников из России, в том числе Руслан Орлов. Найдите вероятность
того, что в первом туре Руслан Орлов будет играть с каким-либо частником из России ?
0,36
ответ
Орлову, очевидно,
с собой не играть !
То, всего исходов
26 - 1= 25 - это n
Событие (А)
из 10
{выбор в пару Орлову из России} россиян
Решение задачи № 9
благоприятствующих исходов
m=9
р(А)
9
25
―

6.

• • что
••Всё
• равно,
• • • • •
ИЛИ

7.

Консультация
Но сначала Ваш ответ
10.Одновременно бросают два кубика. Определите,
5 36
m
n 0,14
p(A)
••
•
•
•
8
Какова вероятность того, что сумма выпавших очков
на двух кубиках равна 8 (ответ округлите до сотых).
Событие (А) {СУММЫ очков 8}
Благоприятных
Кубик I Возможные случаи Кубик II
очков 1 1,2,3,4,5,6,
задачислучаев
№ 10 - суммы очков 8 - m
––
2 – – – – Решение
–– – – – – – –
(2,6) (3,5) (4,4) р(А )
6 ––––––
Всего случаев - n 36
(5,3) (6,2)
11.В случайном эксперименте дважды бросают
игральную кость. Найдите вероятность того,
что сумма выпавших очков будет равной 5.
Результат округлите до сотых.
Событие (А) {СУММЫ очков 5}
••
•
5 :36
условия
•
Сравни
p(A)=0,11
p(A)
Условие: одну кость бросить 2 раза
это, всё равно, что ОДИН раз
Всего событий: 36 - n
каждому числу одной кости
Решение задачи № 11
может быть с 1 по 6 - другой
бросить ДВЕ игральные кости !!!
Благоприятных
событий
- суммы по 5: 1
4
4
1
2
3
3
2
m=4

8.

9
Закрепим приём решения
Сначала Ваш ответ.
12.Какова вероятность выпадения герба подряд два
раза при троекратном подбрасывании монеты?
всё равно, что
один раз
подбрасываются
три монеты
p(A)=0,375
p(A)
Все возможные случаи: Г – герб, Ц– цифра
Г
Г
Г
Г Ц Г
Г Ц Ц
Решение задачи № 12
Ц Г
благоприятные Ц Ц Ц
Г
n=8
Ц Ц Г
Ц Г Ц
Г
Г Ц
m=3
Возможные случаи
ГГГ ГЦГ ГЦЦ ЦГГ ЦЦГ ЦЦЦ ЦГЦ ГГЦ
благоприятные
|
Ещё вариант предъявления решения задачи № 12m = 3
n=8

9.

10
Решить самостоятельно
15. Игральный кубик (кость) бросили один раз. Найдите вероятность
того, что выпало число очков больше, чем 3.
Событие (А) { число очков больше, чем 3}
Всего исходов: n = 6
Проверьте себя, решив задачу
Благоприятных исходов m = 3 (4, 5, 6)
Вероятность 3 : 6 = 0,5
16.Монету подбросили два раза. Найдите вероятность того, что оба
раза выпал орёл.
Событие (А) { орёл выпал ДВА раза}
Всего исходов: n = 4
Проверьте себя, решив задачу
Благоприятных исходов m = 1 (О, О,)
Вероятность 1 : 4 = 0,25

10.

Самостоятельно
18 В случайном эксперименте
ИЛИ
симметричную монету бросают дважды.
Найдите вероятность того, что орел
выпадет ровно один раз.
0.5
19 В случайном эксперименте
Ваши ответы
симметричную монету бросают трижды.
Найдите вероятность того, что орел
не выпадет ни разу.
0.125
Всего исходов (n) 16
20 В случайном эксперименте
20·2·2
и 21
6³ №2·2
симметричную монету бросают четырежды.
(решение
– СЛАЙД 12,13)
Найдите вероятность того, что орел
Благоприятных
(m)1
(РРР)
не выпадет ни разу.
0.0625
21 В случайном эксперименте
• • что
••Всё
• равно,
• • • • •
Игральную кость бросают три раза.
Найдите вероятность того, что
в сумме выпадет 4 очка.
Результат округлите до сотых. 0,01
11

11.

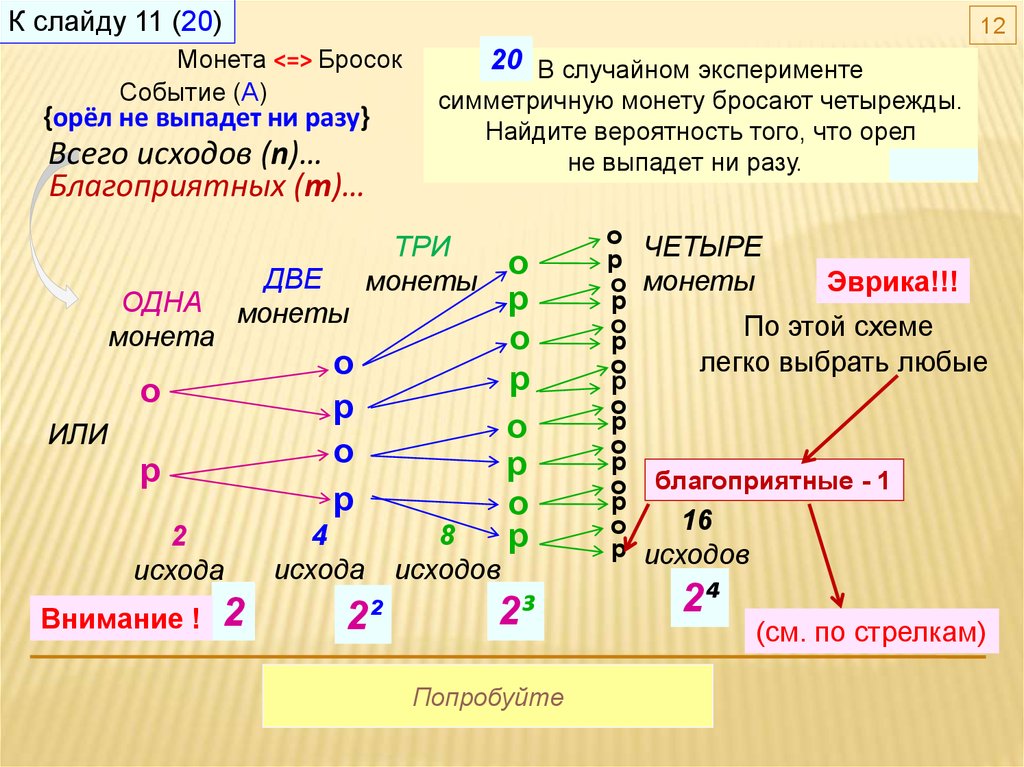
К слайду 11 (20)
12
Монета <=> Бросок
Событие (А)
{орёл не выпадет ни разу}
Всего исходов (n)…
Благоприятных (m)…
ДВЕ
монеты
ОДНА
монета
симметричную монету бросают четырежды.
Найдите вероятность того, что орел
не выпадет ни разу.
0.0625
ТРИ
монеты
о
р
о
р
о
ИЛИ
р
2
исхода
Внимание !
20 В случайном эксперименте
2
4
исхода
2²
8
исходов
о
р
о
р
о
р
о
р
2³
о
р ЧЕТЫРЕ
Эврика!!!
о монеты
р
о
По этой схеме
р
легко выбрать любые
о
р
о
р
о
р
о благоприятные - 1
р
16
о
р исходов
2⁴
СоставьтеПопробуйте
свою задачу и решите
(см. по стрелкам)

12.

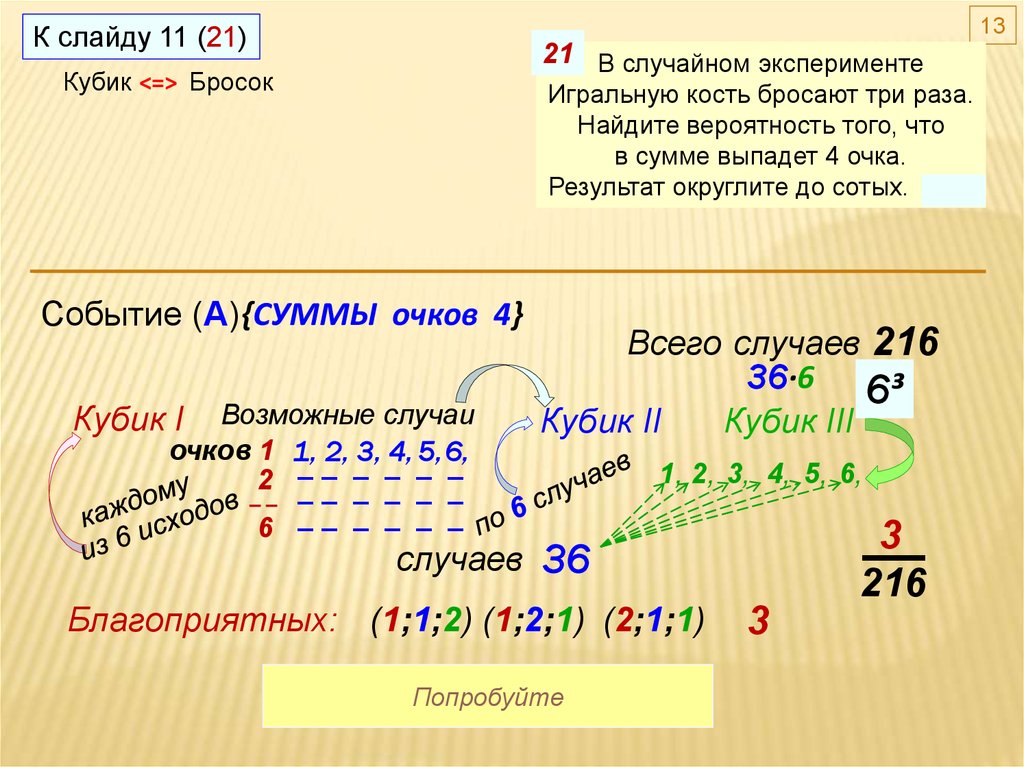
13
К слайду 11 (21)
21 В случайном эксперименте
Кубик <=> Бросок
Игральную кость бросают три раза.
Найдите вероятность того, что
в сумме выпадет 4 очка.
Результат округлите до сотых. 0,01
Событие (А) {СУММЫ очков 4}
Возможные случаи
очков 1 1, 2, 3, 4, 5, 6,
2 –– – – – –
–– – – – – – –
6 –– – – – –
Кубик I
Всего cлучаев 216
36·6
6³
Кубик II
Кубик III
1, 2, 3, 4, 5, 6,
―
3
216
cлучаев 36
Благоприятных: (1;1;2) (1;2;1) (2;1;1)
СоставьтеПопробуйте
свою задачу и решите
3

13.

14
КЛЮЧ ОТВЕТОВ к заданиям файла - приложения
(стр. 1) В10. Вероятность 2012. Все прототипы.
1- 0,2; 2 - 0,6; 3 - 0,3; 4 - 0,2; 5 - 0,36; 6 - 0,9; 7- 0,14; 8 - 0,5;
9 - 0,25; 10 - 0,955 ; 11 - 0,92; 12 - 0,36; 13 - 0,3
(стр. 2) В10. Задания из открытого банка - на ПРОТОТИПАХ
(каждого вида по 47, отличающихся числовыми параметрами)
1 - 0,99; 2 - 0,992; 3 - 0,0625; 4 - 0,03; 5 -0,46; 6 - 0,99; 7- 0,96; 8 - 0,15;
9 - 0,1; 10 - 0,325 ; 11 - 0,25; 12 - 0,04; 13 - 0,12 , 14 - 0,35 ;15 - 0,24

14.

Используемые ресурсы:
В 10 http://mathege.ru/or/ege/ShowProblems.html?posMask=8192
Открытый банк заданий по математике (2012)
http://miranimashek.com/index/0-92
Комментарии http://live.mephist.ru/show/mathege2010/view/B10/all/
Ответы ко всем задачам ЕГЭ по математике 2010 года
Здесь можно общаться
Монеты
http://trinixy.ru/2008/10/30/samye_dorogie_sovremennye_monety_rossii_12_shtuk__tekst.html
Теория и примеры
http://sdo.uspi.ru/mathem&inform/dopoln/dop_lek4/dop_lek4.htm#решение_задач

15.

16
Конкурс исполнителей проводится в 3 дня. Всего заявлено 40 выступлений - по
одному от каждой страны. В первый день 14 выступлений, остальные распределены
поровну между оставшимися днями. Порядок выступлений определяется
жеребьёвкой. Какова вероятность, что выступление представителя России состоится
в третий день конкурса?
Ответ:0,325.
Перед началом первого тура чемпионата по шахматам участников разбивают на
игровые пары случайным образом с помощью жребия. Всего в чемпионате
участвует 26 шахматистов, среди которых 14 участников из России, в том числе Егор
Косов. Найдите вероятность того, что в первом туре Егор Косов будет играть с какимлибо шахматистом из России?
Ответ: 0,52.
Фабрика выпускает сумки. В среднем на 140 качественных сумок приходится десять
сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка
окажется качественной. Результат округлите до сотых.
Ответ: 0,93
В среднем из 1500 садовых насосов, поступивших в продажу, 9 подтекают. Найдите
вероятность того, что один случайно выбранный для контроля насос не подтекает.
Ответ: 0,994
В соревнованиях по толканию ядра участвуют 9 спортсменов из Греции, 3
спортсмена из Болгарии, 10 спортсменов из Румынии и 8 — из России. Порядок, в
котором выступают спортсмены, определяется жребием. Найдите вероятность того,
что спортсмен, который выступает последним, окажется из Болгарии.
Ответ: 0,1