13_Нечеткая логика

1. Нечеткая логика

1

2.

• Лотфи Заде – основатель
научной теории, написавший
в
1965
году
фундаментальный
труд
«Fuzzy Sets». Он описал свой
подход в 1973 году в тексте
«Outline of a New Approach to
the Analysis of Complex
Systems
and
Decision
Processes» (опубликованном в
журнале IEEE Transactions on
Systems). Примечательно, что
сразу после его выхода одна
предприимчивая
датская
фирма успешно применила
изложенные в нем принципы
для
усовершенствования
своей системы управления
сложным производственным
процессом.
04.02.1921 – 06.09.2017 гг.
2

3.

• Английский математик Э.
Мамдани
(Ebrahim
Mamdani) в 1975 году
разработал
алгоритм,
который был предложен в
качестве
метода
для
управления
паровым
двигателем. Предложенный
им алгоритм, основанный
на нечетком логическом
выводе, позволил избежать
чрезмерно большого объема
вычислений. Этот алгоритм
в настоящее время получил
наибольшее практическое
применение
в
задачах
нечеткого моделирования.
01.06.1942 – 22.01.2010 гг.
3

4.

Технологические решения, базирующиеся на нечеткой логике, используются
в следующих областях:
• - распознавание рукописных символов в карманных компьютерах
(записных книжках) (Sony);
• - однокнопочное управление стиральными машинами (Matsushita,
Hitatchi);
• - распознавание рукописных текстов, объектов, голоса (CSK, Hitachi,
Hosai Univ., Ricoh);
• - управление метрополитенами для повышения удобства вождения,
точности остановки и экономии энергии (Hitachi);
• - оптимизация потребления бензина в автомобилях (NOK, Nippon Denki
Tools);
• - повышение чувствительности и эффективности управления лифтами
(Fujitec, Hitachi, Toshiba);
• - эффективное и стабильное управление автомобильными двигателями,
управление экономичной скоростью автомобилей (Nissan, Subaru);
• - оптимизированное планирование автобусных расписаний (Toshiba);
• - системы архивации документов (Mitsubishi Elec.);
• - системы прогнозирования землетрясений (Japan);
• - диагностика рака (Kawasaki Medical School).
4

5.

Системы нечеткого вывода позволяют
решать задачи:
• автоматического управления;
• классификации данных;
• распознавания образов;
• принятия решений;
• машинного обучения и многие другие.
5

6.

Основные понятия и определения нечеткой
логики
• Нечеткое
множество
A определяется
как
множество упорядоченных пар A={μA(х)/х}, где
μA(х)
характеристическая
функция
принадлежности
(или
просто
функция
принадлежности), принимающая значения в
некотором вполне упорядоченном множестве M
(например, M = [0,1]).
• Функция принадлежности указывает степень (или
уровень) принадлежности элемента x множеству A.
• Множество
M
называют
множеством
принадлежностей. Если M = {0,1}, то нечеткое
множество A может рассматриваться как обычное
или четкое множество.
6

7. Наибольшее распространение получили: треугольная, трапецеидальная, гауссова функции принадлежности. Треугольная функция

принадлежности
определяется тройкой чисел (a,b,c), и ее
значение в точке x вычисляется согласно
выражению:
7

8.

• При (b-a)=(c-b) имеем случай
симметричной треугольной функции
принадлежности, которая может быть
однозначно задана двумя параметрами из
тройки (a,b,c).
8

9.

• Аналогично для задания трапецеидальной
функции принадлежности необходима четверка
чисел (a,b,c,d):
• При (b-a)=(d-c) трапецеидальная функция
принадлежности принимает симметричный вид.
Типовые кусочно-линейные функции принадлежности
9

10.

• Трапецеидальная функция принадлежности
• описывается формулой:
10

11.

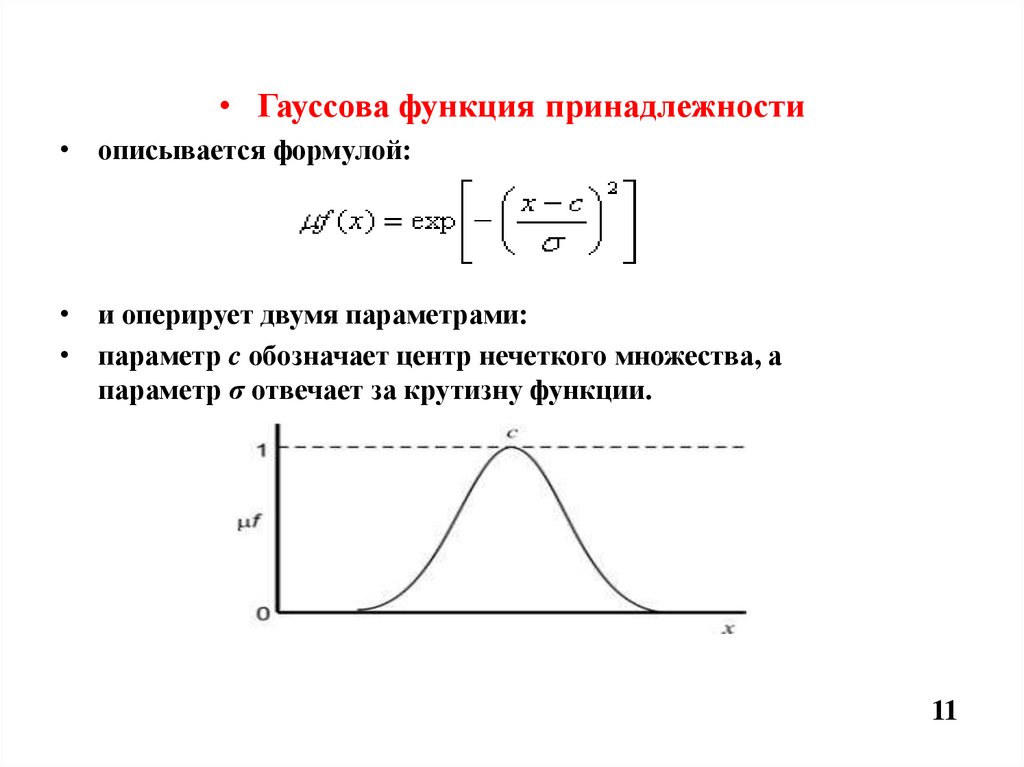
• Гауссова функция принадлежности
• описывается формулой:
• и оперирует двумя параметрами:
• параметр c обозначает центр нечеткого множества, а
параметр σ отвечает за крутизну функции.
11

12.

Нечеткая переменная
характеризуется тройкой <a, X, A>,
где:
a - наименование переменной,
X - универсальное множество (область определения a),
A - нечеткое множество на X, описывающее
ограничения (т.е. μ(x)) на значения нечеткой
переменной a.
12

13.

Лингвистической переменной называется набор <b ,T,X,G,M>,
где:
b - наименование лингвистической переменной;
Т - множество ее значений (терм-множество), представляющих
собой наименования нечетких переменных, областью определения
каждой из которых является множество X. Множество T называется
базовым терм-множеством лингвистической переменной;
G - синтаксическая процедура, позволяющая оперировать
элементами терм-множества T, в частности, генерировать новые термы
(значения). Множество T U G(T), где G(T) - множество сгенерированных
термов, называется расширенным терм-множеством лингвистической
переменной;
М - семантическая процедура, позволяющая превратить каждое
новое значение лингвистической переменной, образуемое процедурой G,
в нечеткую переменную, т.е. сформировать соответствующее нечеткое
множество.
13

14.

Совокупность функций принадлежности для
каждого терма из базового терм-множества T одной
лингвистической переменной обычно изображаются
вместе на одном графике.
Пример: нечеткое понятие “Влажность зерна”. Это
название лингвистической переменной.
Сформируем для нее базовое терм-множество,
которое будет состоять из трех нечетких
переменных: "Низкая", "Умеренная", "Высокая" и
зададим область рассуждений в виде X=[0;100] (%).
Последнее, что осталось сделать – построить x (i )j
функции принадлежности для каждого
лингвистического терма из базового терммножества T.
14

15.

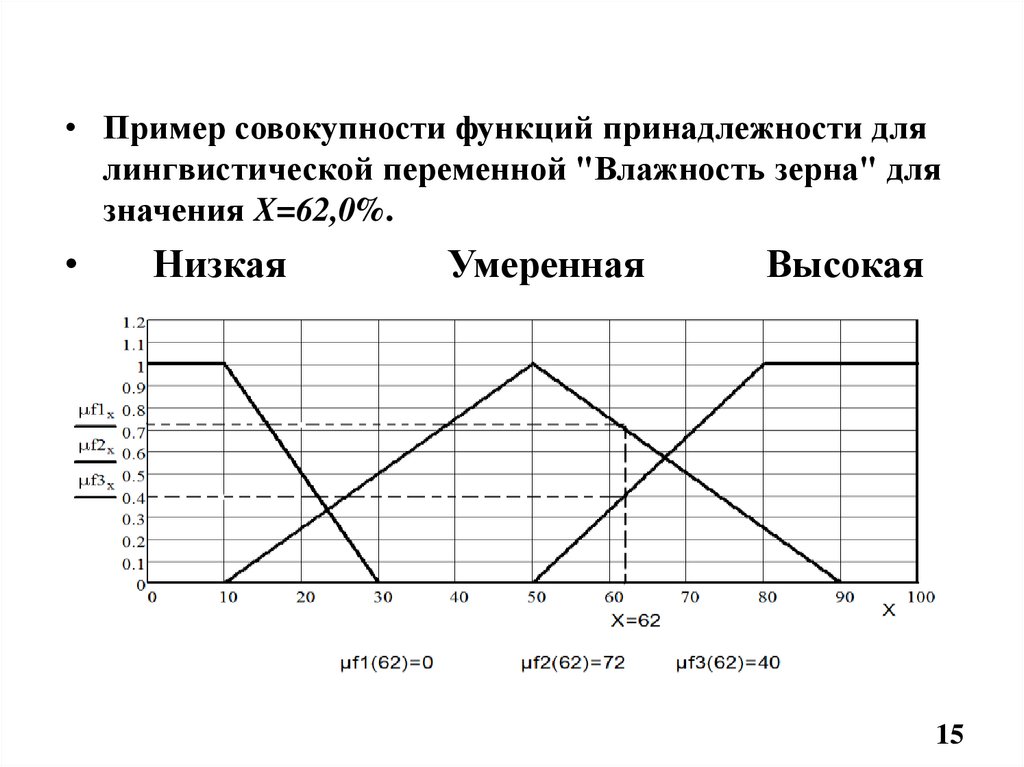
• Пример совокупности функций принадлежности для
лингвистической переменной "Влажность зерна" для
значения X=62,0%.
Низкая
Умеренная
Высокая
15

16.

• Нечеткие числа - нечеткие переменные, определенные на
числовой оси, т.е. нечеткое число определяется как нечеткое
множество А на множестве действительных чисел R с
функцией принадлежности μA(x)€[0,1], где x действительное число, т.е. x € R.
• Нечеткими высказываниями будем называть
высказывания следующего вида:
• Высказывание <b есть b'>, где b - наименование
лингвистической переменной, b' - ее значение, которому
соответствует нечеткое множество на универсальном
множестве Х.
• Высказывание <b есть mb'>, где m - модификатор, которому
соответствуют слова "ОЧЕНЬ", "БОЛЕЕ ИЛИ МЕНЕЕ",
"МНОГО БОЛЬШЕ" и др.
• Составные высказывания, образованные из высказываний
видов 1. и 2. и союзов "И", "ИЛИ", "ЕСЛИ.., ТО...",
"ЕСЛИ.., ТО.., ИНАЧЕ".
16

17.

• Описание системы с помощью аппарата нечеткой логики
• С помощью нечетких высказываний, содержащих лингвистические
переменные, можно описать поведение системы на естественном
(или близком к естественному) языке.
• Входные и выходные параметры системы рассматриваются как
лингвистические переменные, а качественное описание процесса
задается совокупностью высказываний следующего вида (правил):
• L1 : если <A1 > то <B1 >,
• L2 : если <A2 > то <B2 >,
• ....................
• Lk : если <Ak > то <Bk >,
• где <Ai>, i=1,2,..,k - составные нечеткие высказывания, определенные
на значениях входных лингвистических переменных, а <Bi>, i =
1,2,..,k - высказывания, определенные на значениях выходных
лингвистических переменных.
17

18.

• Основой для проведения операций нечеткой логики является база
правил, содержащая нечеткие высказывания в форме "Если-то" и
функции принадлежности для соответствующих лингвистических
термов. Они позволяют осуществлять нечеткие выводы. При этом
должны соблюдаться следующие условия:
• 1. Существует хотя бы одно правило для каждого
лингвистического терма выходной переменной.
• 2. Для любого терма входной переменной имеется хотя бы одно
правило, в котором этот терм используется в качестве
предпосылки (левая часть правила).
• Пример подобного правила: если х – низко, то у – высоко.
• Знание эксперта V → Z отражает нечеткое причинное отношение
предпосылки и заключения, поэтому его можно назвать нечетким
отношением и обозначить через R:
• R = V → Z,
• где «→» называют нечеткой импликацией.
18

19.

• В противном случае имеет место неполная база
нечетких правил.
• Пусть в базе правил имеется m правил вида:
• R1: ЕСЛИ x1 это A11 … И … xn это A1n, ТО y это B1 …
• Ri: ЕСЛИ x1 это Ai1 … И … xn это Ain, ТО y это Bi…
• Rm: ЕСЛИ x1 это Ai1 … И … xn это Amn, ТО y это Bm,
• где xk , k=1..n – входные переменные; y – выходная
переменная; Aik – заданные нечеткие множества с
функциями принадлежности.
• Результатом нечеткого вывода является четкое
значение переменной y* на основе заданных четких
значений xk , k=1..n.
19

20. Механизм логического вывода

включает четыре этапа:
1. Введение нечеткости (фазификация). На данном этапе
осуществляется разработка входных и выходных
лингвистических переменных.
2. Нечеткий вывод. Вычисленное значение истинности для
предпосылок каждого правила применяется к заключениям
правил. Это дает нечеткое подмножество для переменной
вывода каждого правила.
3. Композиция. Все нечеткие подмножества, определенные для
каждой переменной вывода (во всех правилах), объединяются
вместе и формируют одно нечеткое подмножество для каждой
переменной вывода.
4. Приведение к четкости или скаляризация (дефазификация)
результата композиции, т.е. переход от нечеткого
подмножества к скалярным значениям. При этом
скаляризация может проводится различными методами,
например, расчетом «центра тяжести» или первого максимума.
20

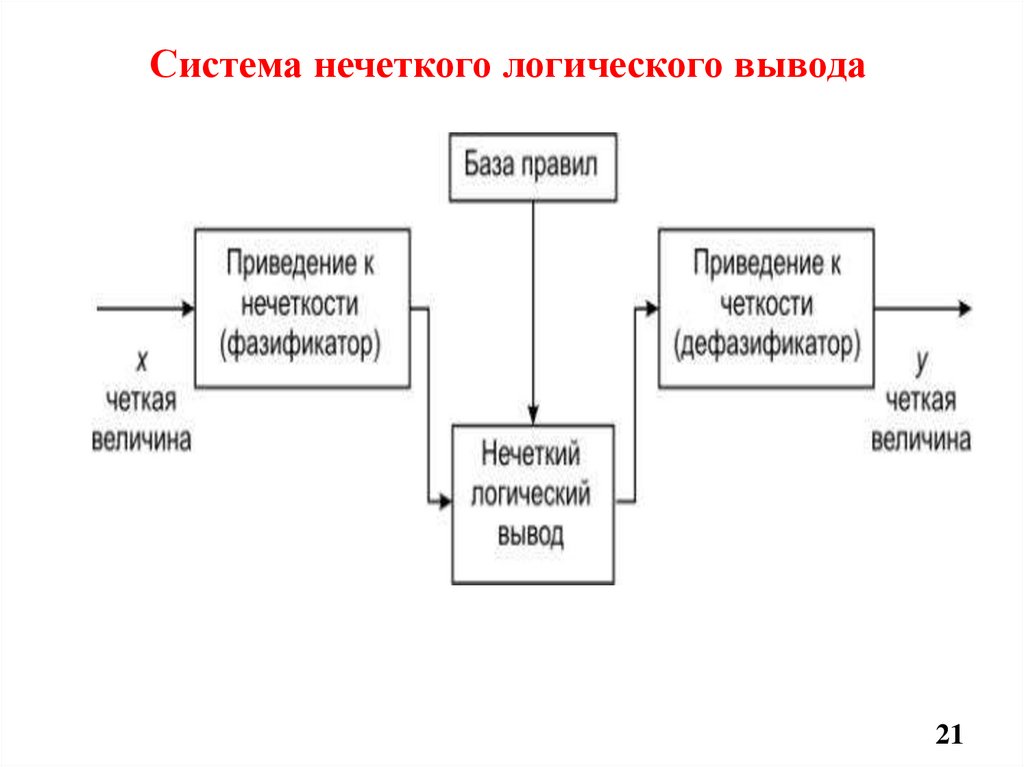
21. Система нечеткого логического вывода

21

22.

• Фаззификация – операция перевода четкой
информации в нечеткую информацию.
• Дефаззификация – операция перевода нечеткой
информации в четкую информацию. Фаззификатор
преобразует точное множество входных данных в
нечеткое множество, определяемое с помощью
значений функций принадлежности, тогда как
дефаззификатор решает обратную задачу – он
формирует однозначное решение относительно
значения выходной переменной на основании многих
нечетких выводов, вырабатываемых исполнительным
модулем нечеткой системы. Выходной сигнал этого
модуля может иметь вид нечетких множеств,
определяющих диапазон изменения выходной
переменной. Дефаззификатор преобразует этот
диапазон в одно конкретное значение, принимаемое в
качестве выходного сигнала всей системы.
22

23. Алгоритмы нечеткого вывода

• Различаются видом используемых правил, логических
операций и разновидностью метода дефазификации.
Разработаны модели нечеткого вывода Мамдани, Сугено,
Ларсена, Цукамото:
• - алгоритм Ларсена (особенность - импликация моделируется с
использованием операции умножения);
• - алгоритм Сугено (особенность - правые части правил вывода
представлены в виде линейных функций);
• - алгоритм Цукамото (особенность - функции принадлежности
являются монотонными);
• - так называемый упрощенный вывод (особенность – правая
часть правил – четкое значение).
• Выбор алгоритма зависит от характера взаимосвязей и
описания нечетких переменных, а также целями
моделирования (интерпретация и объяснение принятого
решения или точность идентификации нелинейных
зависимостей).
23

24. Методы дефаззификации

центр тяжести (centroid),
центр медианы (bisector),
наибольшего из максимумов (lom),
наименьшего из максимумов (som) и центр
максимумов (mom).
• Наиболее распространенный способ логического
вывода – вывод Мамдани, использующий на этапе
дефаззификации метод центроида с целью сокращения
объема вычислений и повышения быстродействия.
• Геометрический смысл такого значения – центр
тяжести для кривой µfc(y).
24

25.

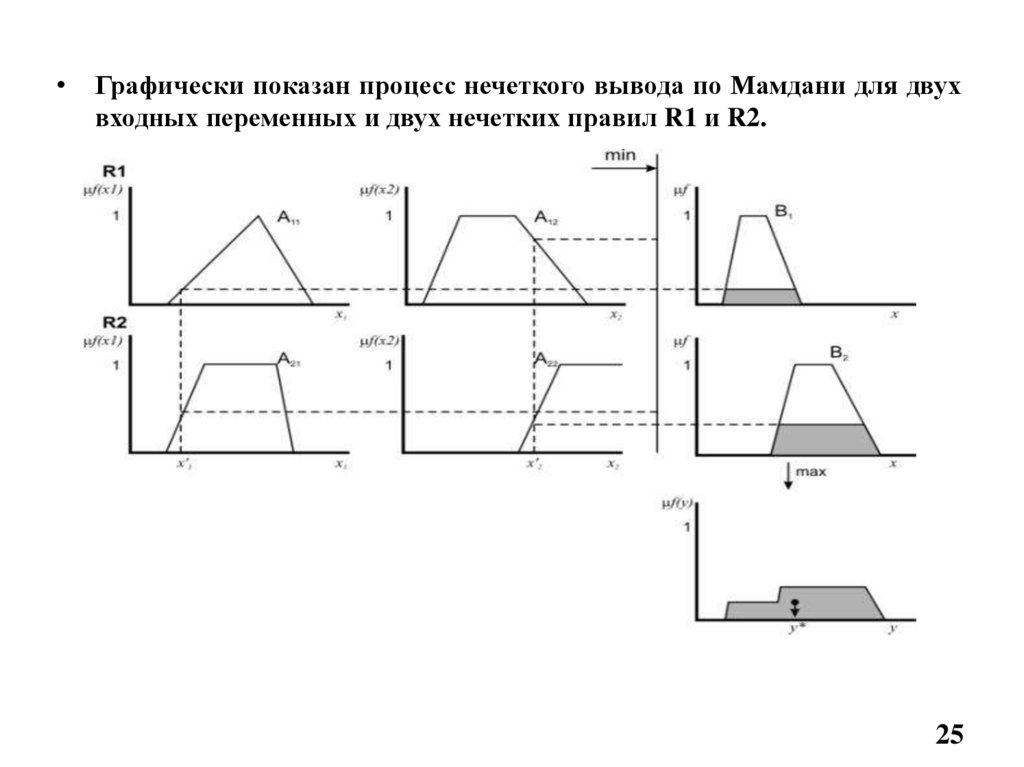
Графически показан процесс нечеткого вывода по Мамдани для двух
входных переменных и двух нечетких правил R1 и R2.
25

26.

Дефаззификатор по центру тяжести
В качестве выходного значения принимается значение у,
соответствующее центру тяжести фигуры, ограниченной функцией
принадлежности и осью абсцисс:
26

27. Пример

управления глубиной погружения в почву рабочего органа
почвообрабатывающей машины при вспашке. Входным точным
значением здесь является плотность почвы ρ, а выходным длительность действия актуатора t – приводного механизма
поступательного движения рабочего органа, определяющего глубину его
погружения в почву.
Введем две лингвистические переменные: "плотность почвы" с
термами "малая", "средняя", "большая" и "длительность
поступательного движения актуатора" с термами "короткая",
"средняя", "большая".
Нечеткая инструкция управлением этой системой может сводиться к
трем простым правилам:
1) при малой плотности длительность поступательного движения
актуатора должна быть короткой (R1),
2) средней плотности должна соответствовать средняя длительность
поступательного движения актуатора (R2),
3) в случае большой плотности требуется большая длительность
поступательного движения актуатора(R3).
27

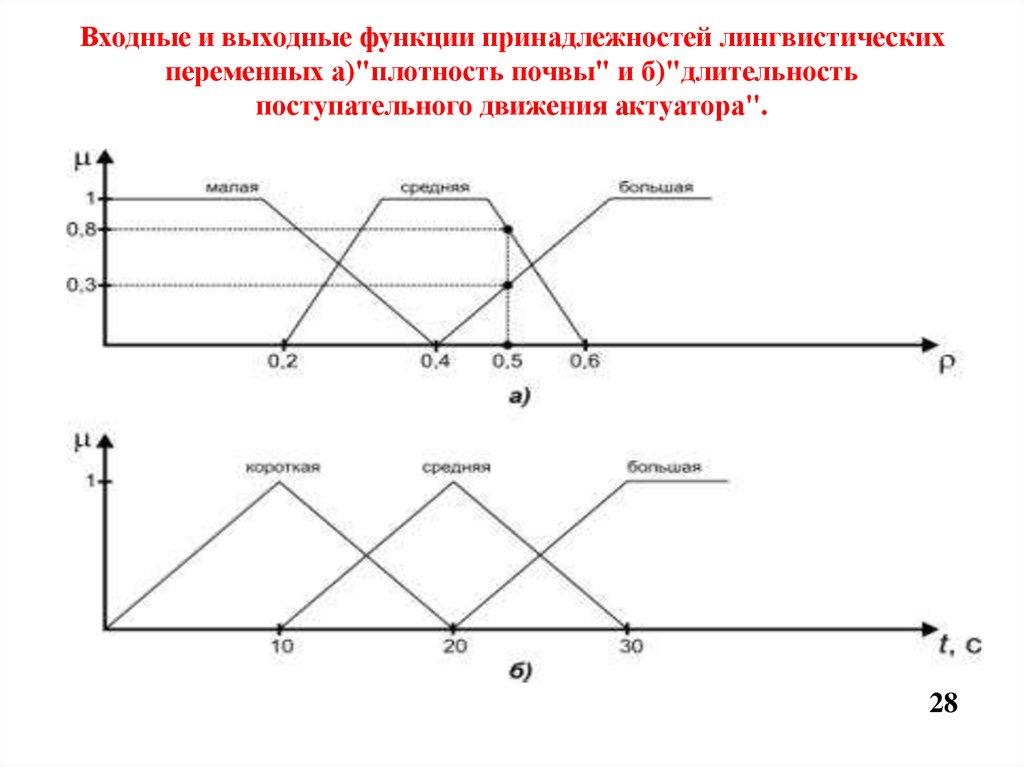
28. Входные и выходные функции принадлежностей лингвистических переменных а)"плотность почвы" и б)"длительность поступательного

Входные и выходные функции принадлежностей лингвистических
переменных а)"плотность почвы" и б)"длительность
поступательного движения актуатора".
28

29. Пример

• Области определения входных функций принадлежности
различных термов пересекаются, поэтому выходная
нечеткая инструкция будет представляться некоторой
комбинацией приведенных правил. При этом естественно
предположить, что в эту комбинацию отдельные правила
будут входить с коэффициентами, определяемыми
степенями принадлежности точных исходных данных
соответствующим термам.
• Пусть зафиксированное в некоторый момент значение
плотности ρ равно 0,5. Процедура фаззификации
показывает, что эта плотность со степенью 0,3 принадлежит
терму "большая плотность" и со степенью 0,8 - терму
"средняя плотность", а к терму «низкая плотность» не
принадлежит. Согласно принятому правилу
комбинирования нечетких выходных инструкций,
длительность поступательного движения актуатора должна
быть на 0,3 большой и на 0,8 средней.
29

30. Пример

• Применим центроидный метод дефаззификации:
• где tб и tс – длительности поступательного
движения актуатора, при которых выходные
функции принадлежности соответствующих
термов ("большая" и "средняя") принимают
максимальные значения (соответственно 30 и
20). В нашем случае t = 24,2.
30