Методысортировки

1.

АЛГОРИТМЫ СОРТИРОВКИ
Основные требования к алгоритму сортировки – экономное расходование памяти и быстродействие. Удобная
мера эффективности- подсчет необходимых сравнений (С) и пересылок элементов (М). Эти величины
определяются некоторыми функциями от n –числа элементов.
Хорошие алгоритмы требуют n*log(n)сравнений. Простые методы требуют порядка n2 сравнений. При небольших
n простые методы работают быстрее, но их не следует применять при больших n.
Сортировка обменом
Сортировка выбором
Сортировка вставками

2.

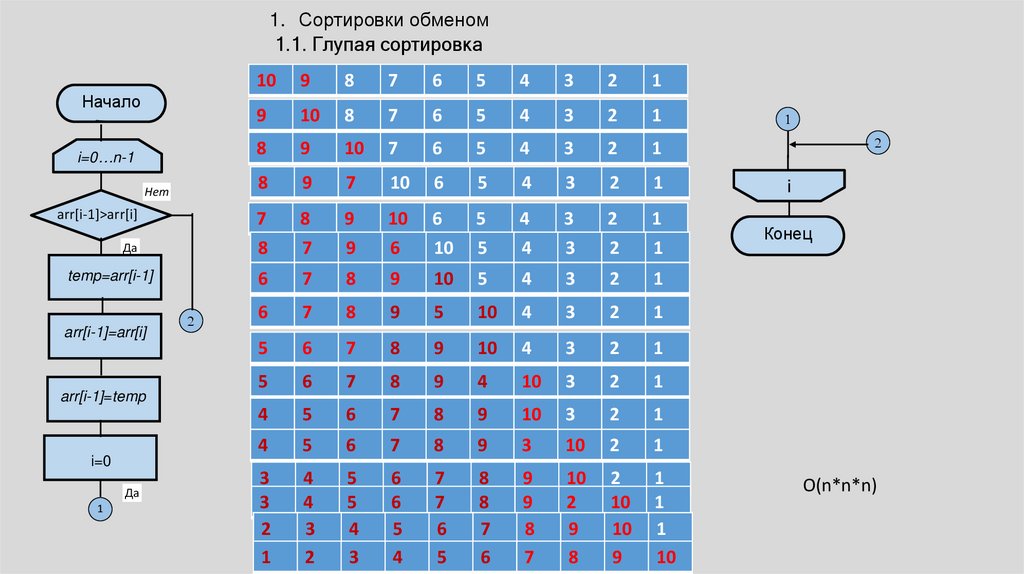
1. Сортировки обменом
1.1. Глупая сортировка
10
9
8
7
6
5
4
3
2
1
9
10
8
7
6
5
4
3
2
1
8
9
10
7
6
5
4
3
2
1
8
9
7
10
6
5
4
3
2
1
arr[i-1]>arr[i]
7
8
9
10
6
5
4
3
2
1
Да
8
7
9
6
10
5
4
3
2
1
6
7
8
9
10
5
4
3
2
1
6
7
8
9
5
10
4
3
2
1
5
6
7
8
9
10
4
3
2
1
5
6
7
8
9
4
10
3
2
1
4
5
6
7
8
10
3
2
1
4
5
6
7
8
9
10
9
3
10
2
1
3
3
2
1
4
4
3
2
5
5
4
3
6
6
5
4
7
7
6
5
8
8
7
6
9
9
8
7
10
2
9
8
2
10
10
9
1
1
1
10
Начало
i=0…n-1
Нет
temp=arr[i-1]
arr[i-1]=arr[i]
arr[i-1]=temp
i=0
Да
1
2
1
2
i
Конец
O(n*n*n)

3.

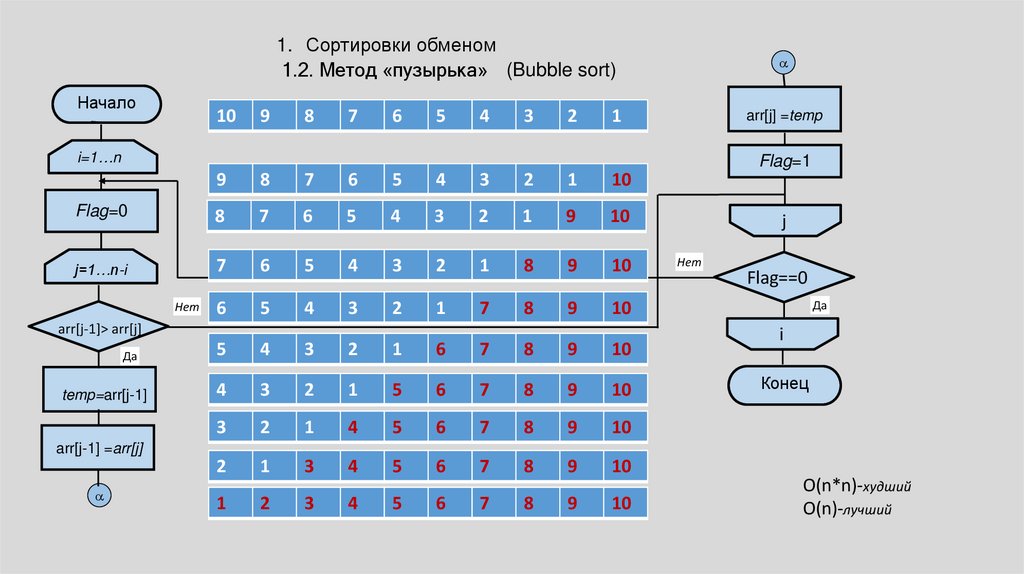
1. Сортировки обменом
1.2. Метод «пузырька» (Bubble sort)
Начало
10
9
8
7
6
5
4
3
2
a
1
arr[j] =temp
i=1…n
Flag=1
9
8
7
6
5
4
3
2
1
10
Flag=0
8
7
6
5
4
3
2
1
9
10
j=1…n-i
7
6
5
4
3
2
1
8
9
10
6
5
4
3
2
1
7
8
9
10
Нет
arr[j-1]> arr[j]
Да
temp=arr[j-1]
5
4
3
2
1
6
7
8
9
10
4
3
2
1
5
6
7
8
9
10
3
2
1
4
5
6
7
8
9
10
2
1
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
j
Нет
Flag==0
Да
i
Конец
arr[j-1] =arr[j]
a
O(n*n)-худший
O(n)-лучший

4.

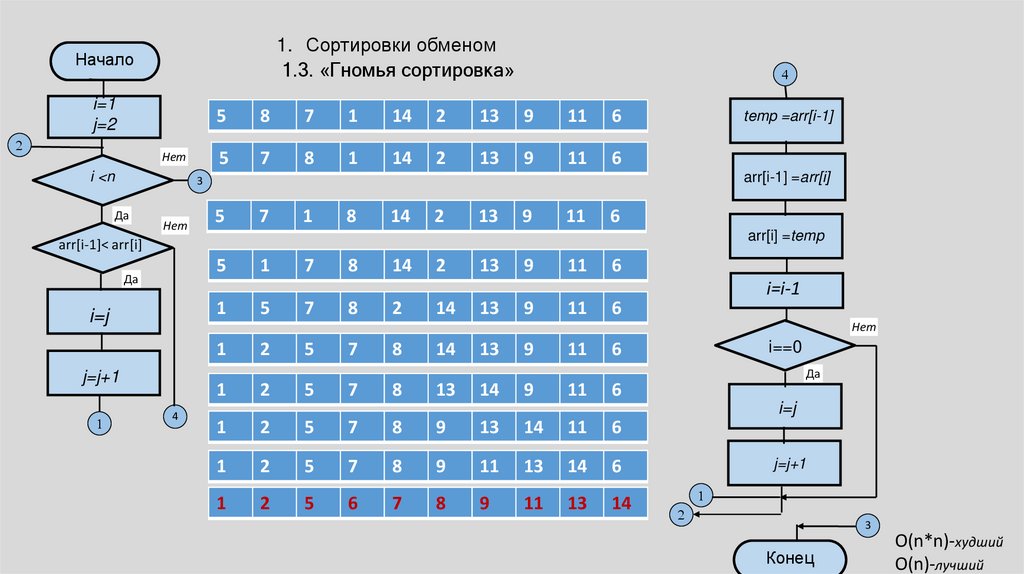
1. Сортировки обменом
1.3. «Гномья сортировка»
Начало
i=1
j=2
2
Нет
i <n
4
5
8
7
1
14
2
13
9
11
6
5
7
8
1
14
2
13
9
11
6
temp =arr[i-1]
arr[i-1] =arr[i]
3
Да
Нет
5
7
1
8
14
2
13
9
11
6
arr[i] =temp
arr[i-1]< arr[i]
5
Да
7
8
14
2
13
9
11
6
i=i-1
1
i=j
5
7
8
2
14
13
9
11
6
Нет
1
2
5
7
8
14
13
9
11
i==0
6
Да
j=j+1
1
1
1
4
2
5
7
8
13
14
9
11
6
i=j
1
2
5
7
8
9
13
14
11
6
1
2
5
7
8
9
11
13
14
6
1
2
5
6
7
8
9
11
13
14
j=j+1
1
2
3
Конец
O(n*n)-худший
O(n)-лучший

5.

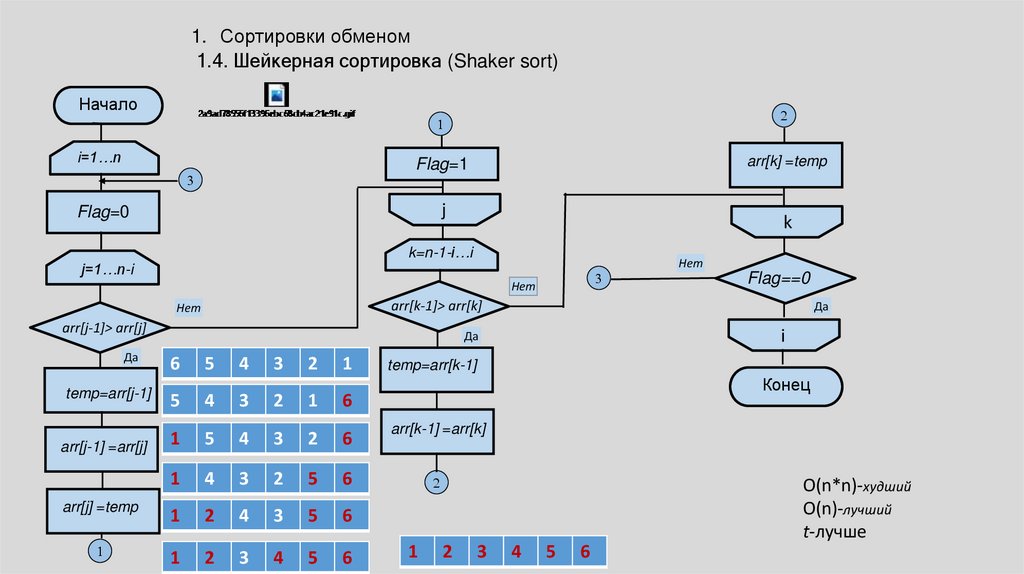
1. Сортировки обменом
1.4. Шейкерная сортировка (Shaker sort)
Начало
2
1
i=1…n
arr[k] =temp
Flag=1
3
j
Flag=0
k
k=n-1-i…i
j=1…n-i
3
Нет
arr[j-1]> arr[j]
temp=arr[j-1]
arr[j-1] =arr[j]
arr[j] =temp
1
Да
i
Да
6
Flag==0
arr[k-1]> arr[k]
Нет
Да
Нет
5
4
3
2
1
5
4
3
2
1
6
1
5
4
3
2
6
1
4
3
2
5
6
1
2
4
3
5
6
1
2
3
4
5
6
temp=arr[k-1]
Конец
arr[k-1] =arr[k]
2
1
O(n*n)-худший
O(n)-лучший
t-лучше
2
3
4
5
6

6.

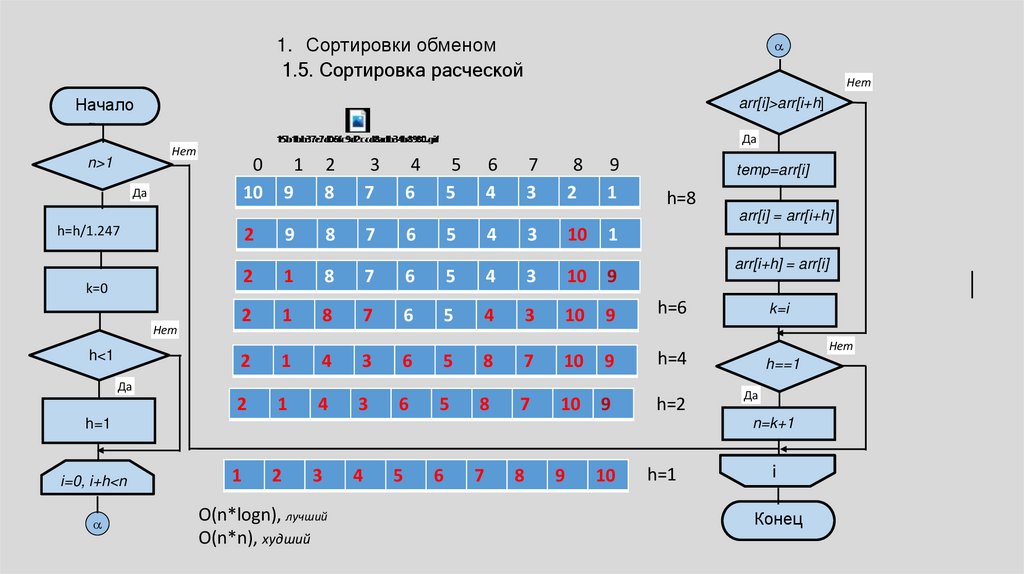
1. Сортировки обменом
1.5. Сортировка расческой
a
Нет
Начало
arr[i]>arr[i+h]
Да
Нет
n>1
0
10
Да
1
9
2
8
3
7
4
6
5
5
6
4
7
3
8
2
9
1
temp=arr[i]
h=8
arr[i] = arr[i+h]
h=h/1.247
k=0
Нет
h<1
2
9
8
7
6
5
4
3
10
1
2
1
8
7
6
5
4
3
10
9
2
1
8
7
6
5
4
3
10
9
h=6
arr[i+h] = arr[i]
2
1
4
3
6
5
8
7
10
9
h=4
2
1
4
3
6
5
8
7
10
9
h=2
Да
a
Нет
h==1
Да
n=k+1
h=1
i=0, i+h<n
k=i
1
2
3
O(n*logn), лучший
O(n*n), худший
4
5
6
7
8
9
10
h=1
i
Конец

7.

1. Сортировки обменом
1.6. Сортировка слиянием

8.

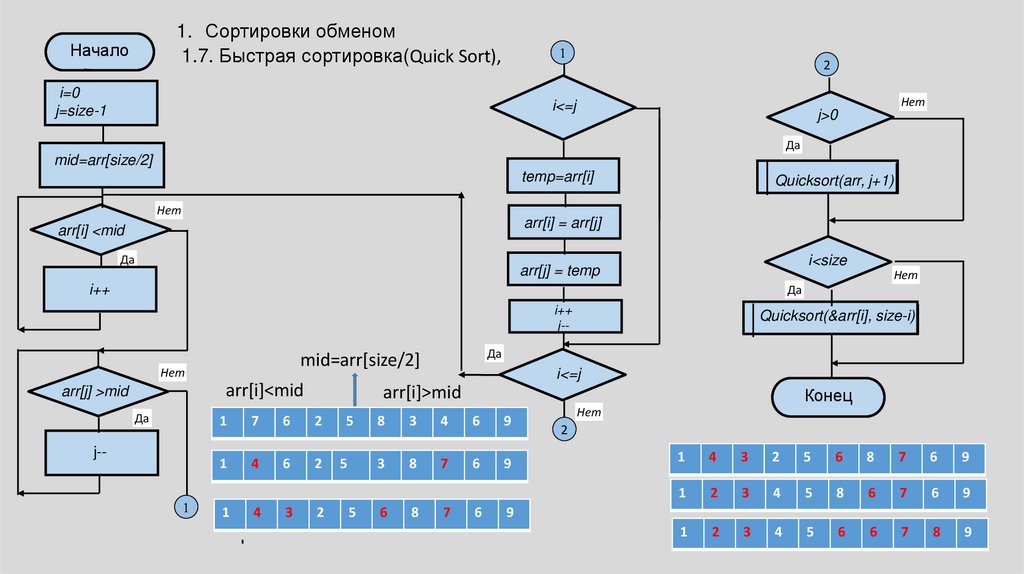
1. Сортировки обменом
1.7. Быстрая сортировка(Quick Sort),
Начало
1
i=0
j=size-1
2
i<=j
Нет
j>0
Да
mid=arr[size/2]
temp=arr[i]
Нет
Quicksort(arr, j+1)
arr[i] = arr[j]
arr[i] <mid
Да
i<size
arr[j] = temp
Нет
i++
Да
i++
j--
arr[i]<mid
arr[j] >mid
Да
j--
1
Да
mid=arr[size/2]
Нет
i<=j
arr[i]>mid
Конец
1
7
6
2
5
8
3
4
6
9
1
4
6
2
5
3
8
7
6
9
1
4
3
Quicksort(&arr[i], size-i)
2
5
6
8
7
6
Нет
2
1
4
3
2
5
6
8
7
6
9
1
2
3
4
5
8
6
7
6
9
1
2
3
4
5
6
6
7
8
9
9

9.

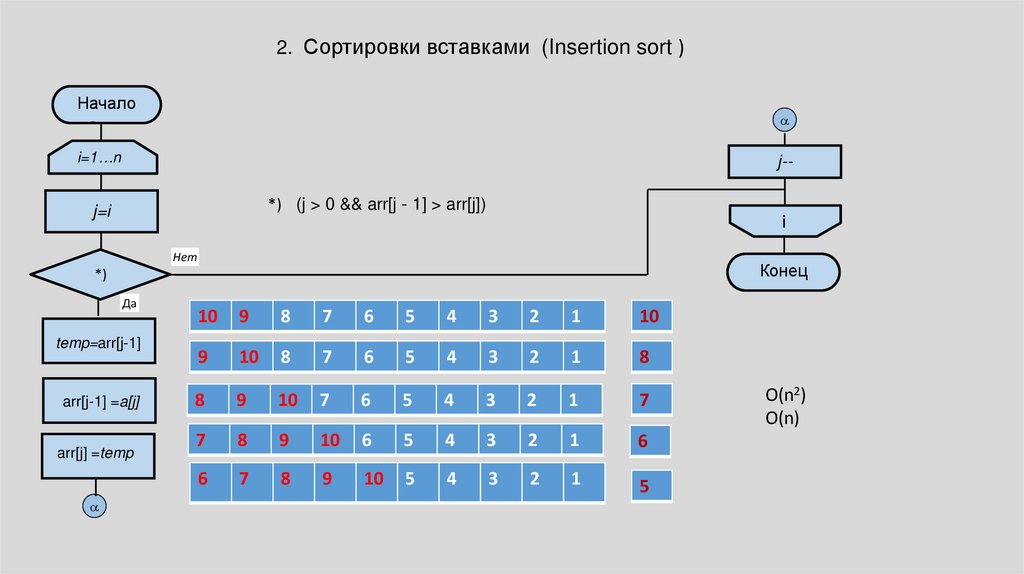
2. Сортировки вставками (Insertion sort )
Начало
a
i=1…n
j-*) (j > 0 && arr[j - 1] > arr[j])
j=i
i
Нет
Конец
*)
Да
temp=arr[j-1]
arr[j-1] =a[j]
arr[j] =temp
a
10
9
8
7
6
5
4
3
2
1
10
9
10
8
7
6
5
4
3
2
1
8
8
9
10
7
6
5
4
3
2
1
7
7
8
9
10
6
5
4
3
2
1
6
6
7
8
9
10
5
4
3
2
1
5
O(n2)
O(n)

10.

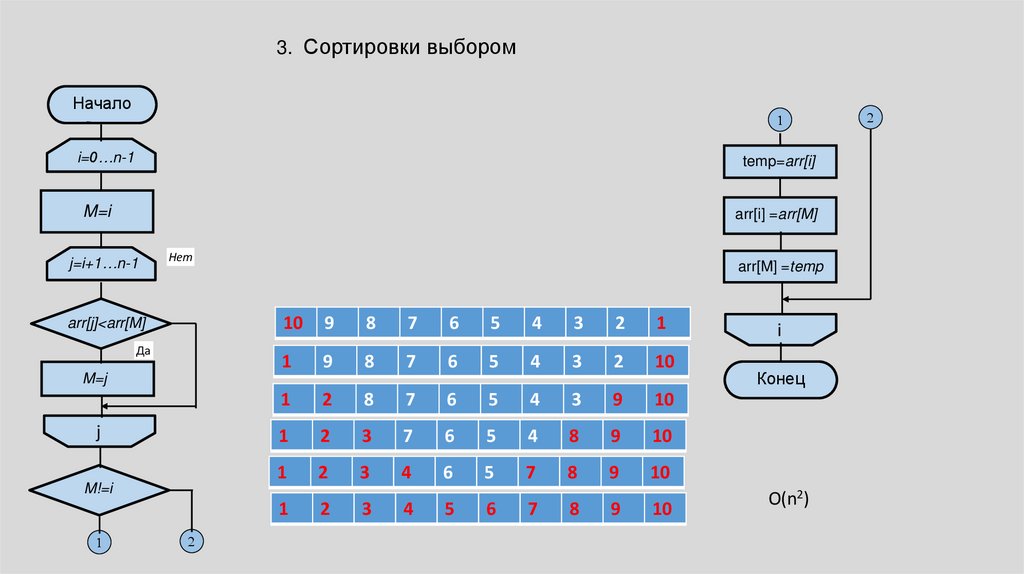
3. Сортировки выбором
Начало
1
i=0…n-1
temp=arr[i]
M=i
arr[i] =arr[M]
j=i+1…n-1
Нет
arr[j]<arr[M]
Да
arr[M] =temp
10
9
8
7
6
5
4
3
2
1
1
9
8
7
6
5
4
3
2
10
1
2
8
7
6
5
4
3
9
10
1
2
3
7
6
5
4
8
9
10
1
2
3
4
6
5
7
8
9
10
M=j
j
M!=i
1
1
2
2
3
4
5
6
7
8
9
10
i
Конец
O(n2)
2

11.

Пирамидальна сортировка
Куча – сбалансированное двоичное дерево.
Все узлы в дереве следуют тому свойству, что они
больше своих потомков, то есть самый большой
элемент находится в корне, и оба его потомка меньше,
чем корень, и так далее. Такая куча называется
убывающая(Max-Heap).
Если вместо этого все узлы меньше своих потомков,
это называется возрастающей кучей (Min-Heap).
a[i] ≤ a[2i+1]; - левый потомок
Просеивание вверх
Просеивание вниз
a[i] ≤ a[2i+2] - правый потомок

12.

Строим из массива дерево:
Пусть индекс элемента в массиве равен i,
тогда индекс левого потомка (2i + 1),
а индекс правого потомка будет (2i + 2)
Индекс родительского элемента для потомка
с индексом i задается нижней границей (i-1) / 2.

13.

Построение пирамиды - рекурсивная процедура. ( void heapify(int arr[], int n, int i))
Тело рекурсии:
выделяем корень,
Если корень Max, ничего не делаем (сценарий 1)
Ищем Max потомка и делаем
его корнем (сценарий 2)

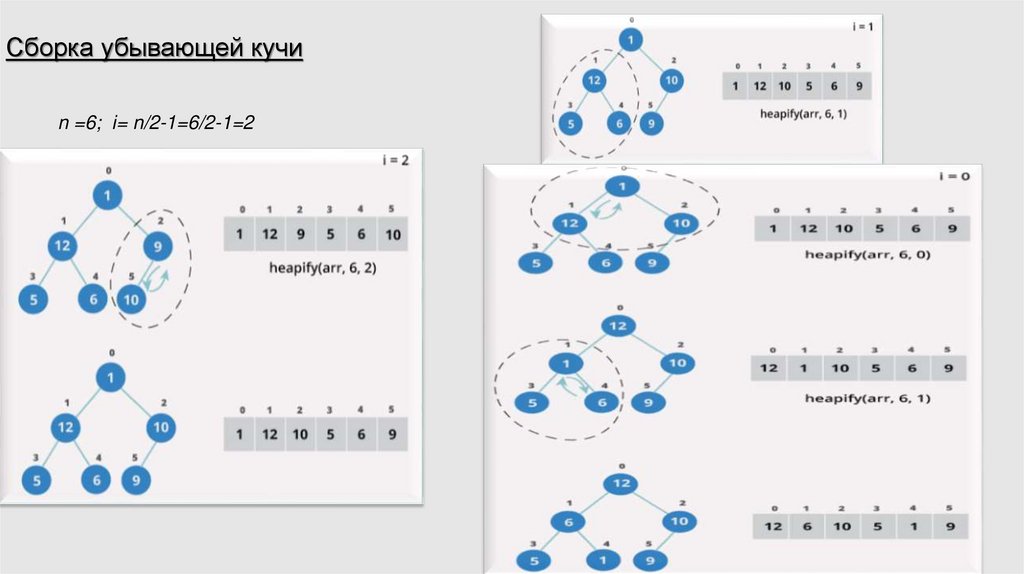
14.

Сборка убывающей кучи
n =6; i= n/2-1=6/2-1=2

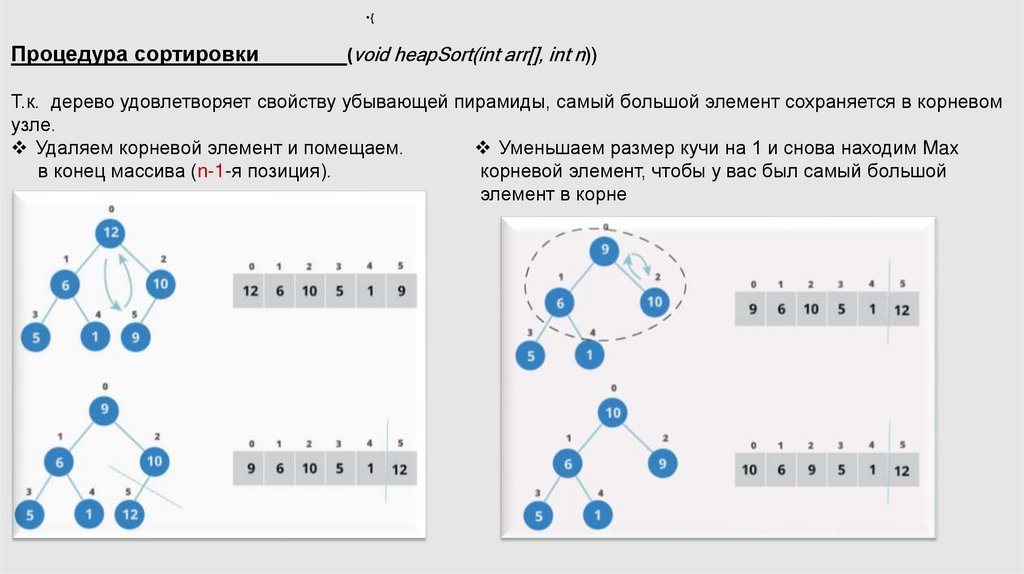
15.

•{
Процедура сортировки
(void heapSort(int arr[], int n))
Т.к. дерево удовлетворяет свойству убывающей пирамиды, самый большой элемент сохраняется в корневом
узле.
Уменьшаем размер кучи на 1 и снова находим Max
Удаляем корневой элемент и помещаем.
корневой элемент, чтобы у вас был самый большой
в конец массива (n-1-я позиция).
элемент в корне

16.

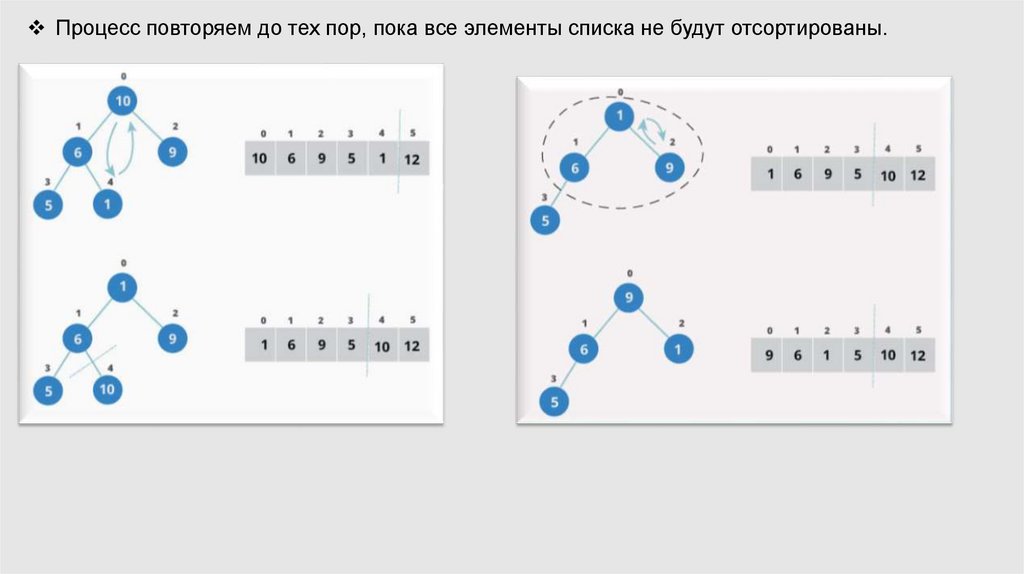
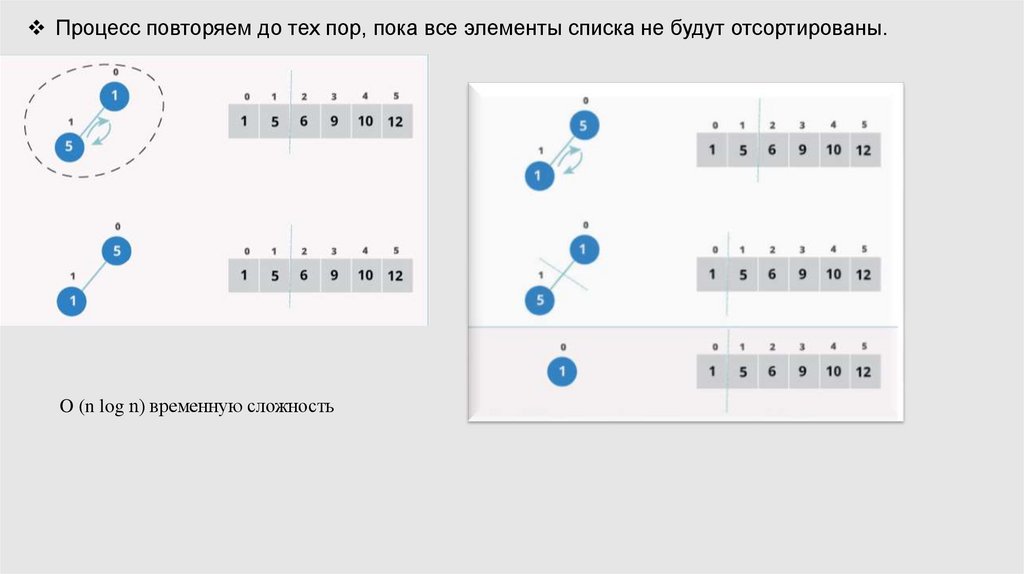
Процесс повторяем до тех пор, пока все элементы списка не будут отсортированы.

17.

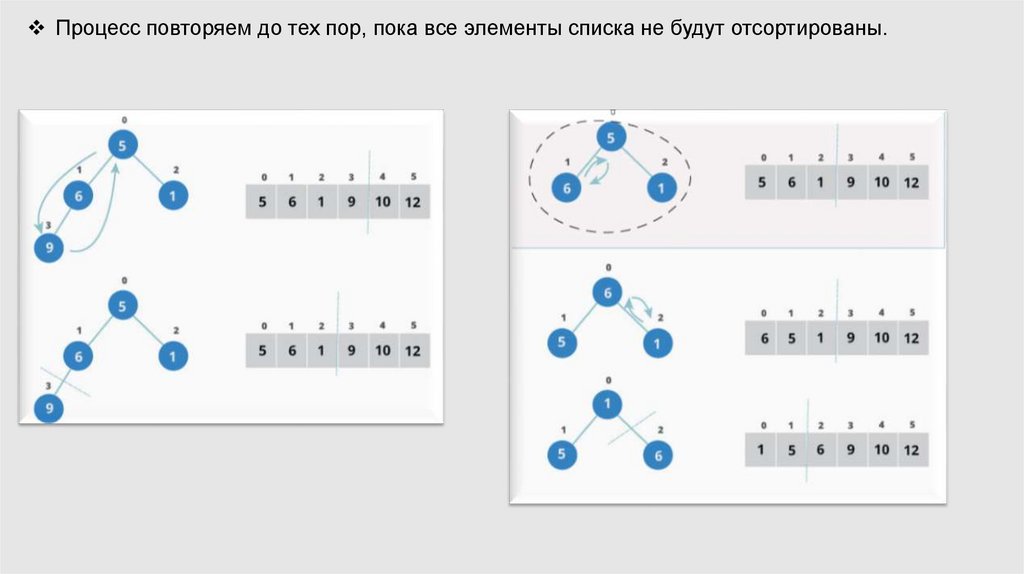
Процесс повторяем до тех пор, пока все элементы списка не будут отсортированы.

18.

Процесс повторяем до тех пор, пока все элементы списка не будут отсортированы.
O (n log n) временную сложность

19.

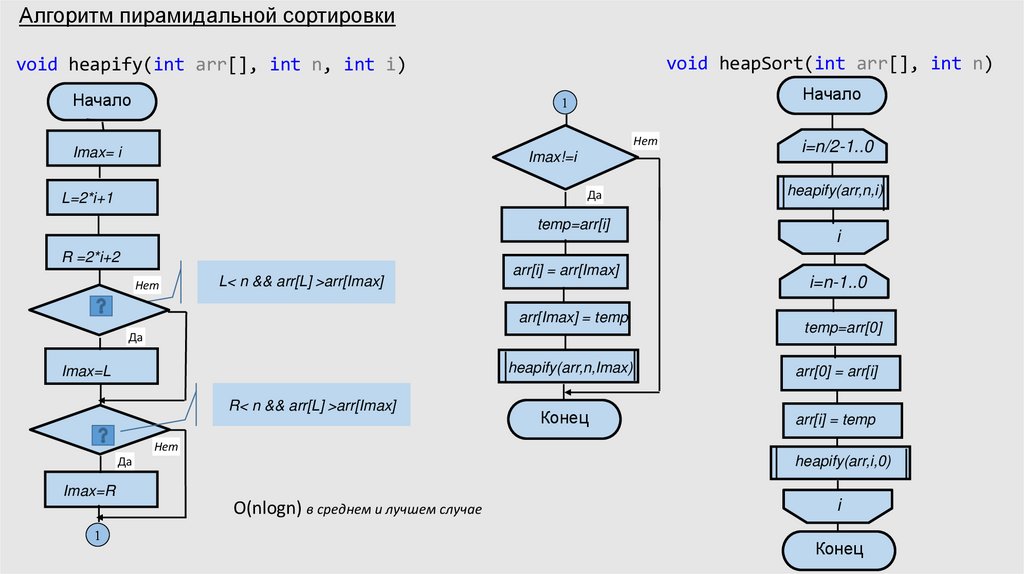
Алгоритм пирамидальной сортировки
void heapSort(int arr[], int n)
void heapify(int arr[], int n, int i)
Начало
Начало
1
Нет
Imax= i
Imax!=i
Да
L=2*i+1
temp=arr[i]
R =2*i+2
Нет
L< n && arr[L] >arr[Imax]
arr[i] = arr[Imax]
arr[Imax] = temp
Да
Imax=L
R< n && arr[L] >arr[Imax]
i=n/2-1..0
heapify(arr,n,i)
i
i=n/2-1..0
i=n-1..0
temp=arr[0]
heapify(arr,n,Imax)
arr[0] = arr[i]
Конец
arr[i] = temp
Нет
heapify(arr,i,0)
Да
Imax=R
O(nlogn) в среднем и лучшем случае
1
i
Конец

20.

Исследование алгоритмов сортировки
Три вида последовательностей:
Изначально отсортированная возрастающая последовательность
1 2 3 4 5 6 7 8 9 10….
Изначально отсортированная убывающая последовательность
… 10 9 8 7 6 5 4 3 2 1
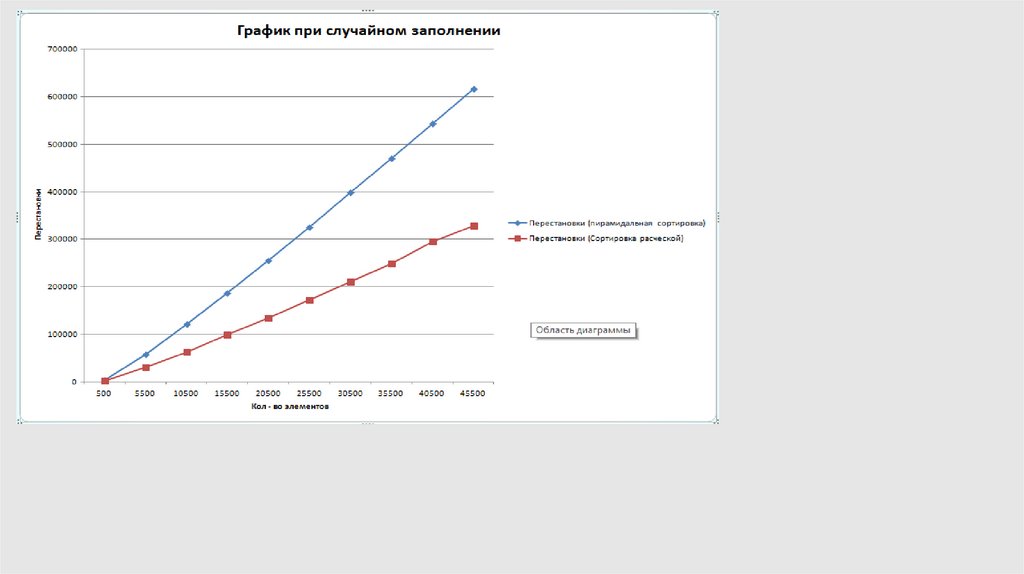
Произвольная последовательность
Оцениваемые параметры ( в зависимости от количества элементов):
Время
Количество сравнений
Количество перестановок