лекция 2 курс (1)

1. Лекция

Алгоритмизация и программирование
Лекция
Основы языка

2.

Лабораторная
Работа №4
2

3.

Задание:
Реализовать свои собственные классы для коллекций List, Stack,
Queue, LinkedList*.
В качестве буфера для хранения использовать обычные массивы.
Обязательные методы класса MyList:
Add – добавить элемент
AddRange – добавить коллекцию
Clear - очистить
Contains – проверить, содержит ли
IndexOf – индекс первого вхождения
Insert – вставка
InsertRange – вставка коллекции
LastIndexOf – индекс последнего
вхождения
Remove – удаление
RemoveAt – удаление по индексу
RemoveRange
–
удаление
последовательности
Sort – сортировка
Reverse – переворот
Count – количество элементов
(свойство)
Получение значения по индексу [ ]
3

4.

Задание:
Реализовать свои собственные классы для коллекций List, Stack,
Queue, LinkedList*.
В качестве буфера для хранения использовать обычные массивы.
Обязательные методы класса MyStack:
Push – добавить элемент в стек
Pop – извлечь элемент из стека
Peek – вернуть значение элемента без извлечения
Count – количество элементов (свойство)
Обязательные методы класса MyQueue:
EnQueue – добавить элемент в очередь
Dequeue – извлечь элемент из очереди
Peek – вернуть значение элемента без извлечения
Count – количество элементов (свойство)
4

5.

Задание:
Реализовать свои собственные классы для коллекций List, Stack,
Queue, LinkedList*.
В качестве буфера для хранения использовать обычные массивы.
Обязательные методы класса MyLinkedList:
• AddFirst,
• AddLast,
Свойства класса MyLinkedListNode:
• AddAfter,
• List
• AddBefore,
• Next
• Remove
• Previous
• RemoveFirst,
• Value
• RemoveLast.
Свойства: Count, Last, First
5

6.

РасчетноГрафическая
Работа
6

7.

Сложность алгоритмов обычно оценивают по времени выполнения
или по используемой памяти.
В обоих случаях сложность зависит от размеров входных данных:
массив из 100 элементов будет обработан быстрее, чем аналогичный из
1000.
При этом точное время мало кого интересует: оно зависит от
процессора, типа данных, языка программирования и множества других
параметров.
Важна лишь асимптотическая сложность, т. е. сложность при
стремлении размера входных данных к бесконечности.
7

8.

Допустим, некоторому алгоритму нужно выполнить
4n3 + 7n
условных операций, чтобы обработать n элементов входных данных.
При увеличении n на итоговое время работы будет значительно
больше влиять возведение n в куб, чем умножение его на 4 или же
прибавление 7n.
Тогда говорят, что временная сложность этого алгоритма равна О(n3),
т. е. зависит от размера входных данных кубически.
8

9.

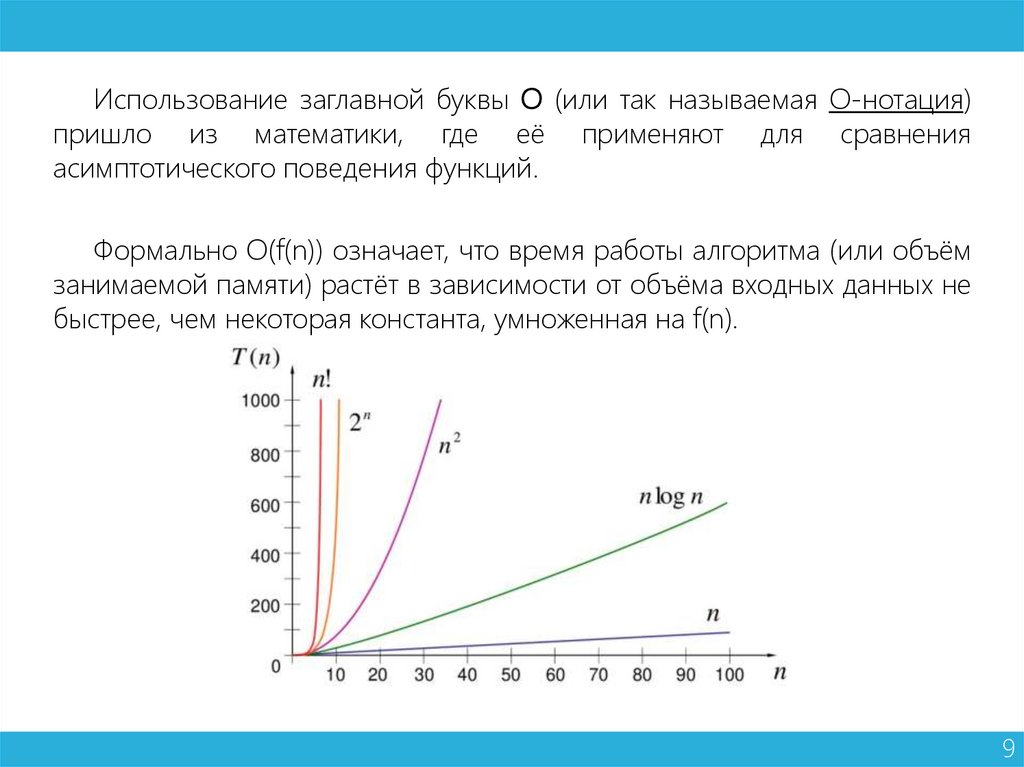
Использование заглавной буквы О (или так называемая О-нотация)
пришло из математики, где её применяют для сравнения
асимптотического поведения функций.
Формально O(f(n)) означает, что время работы алгоритма (или объём
занимаемой памяти) растёт в зависимости от объёма входных данных не
быстрее, чем некоторая константа, умноженная на f(n).
9

10.

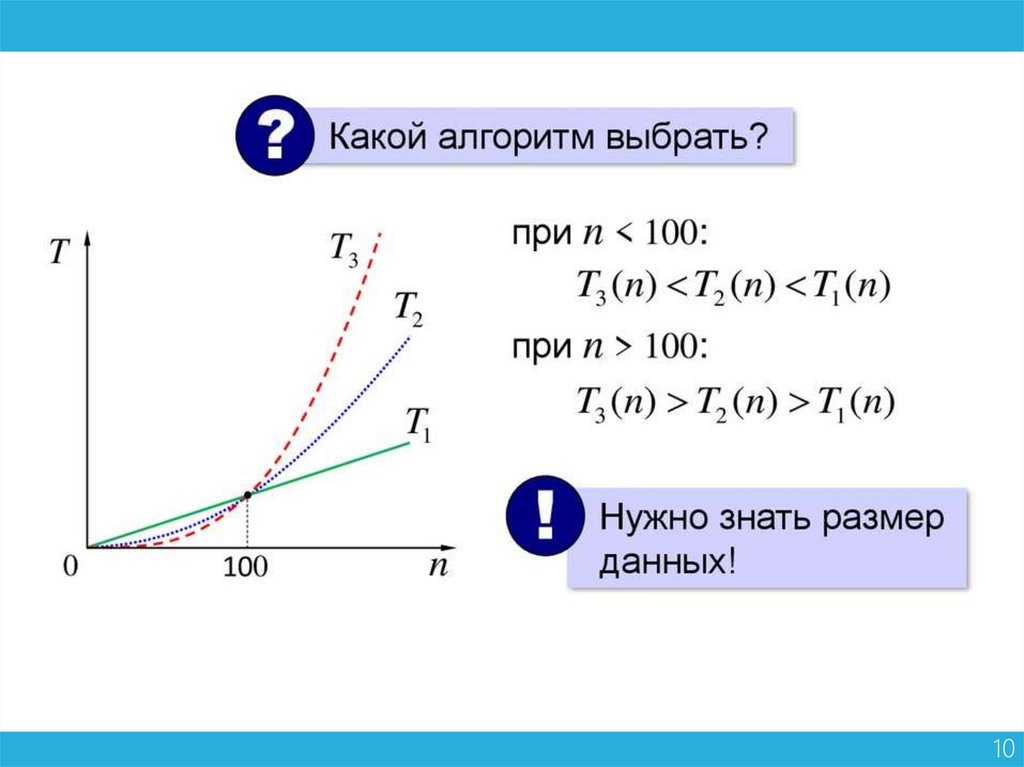
10

11.

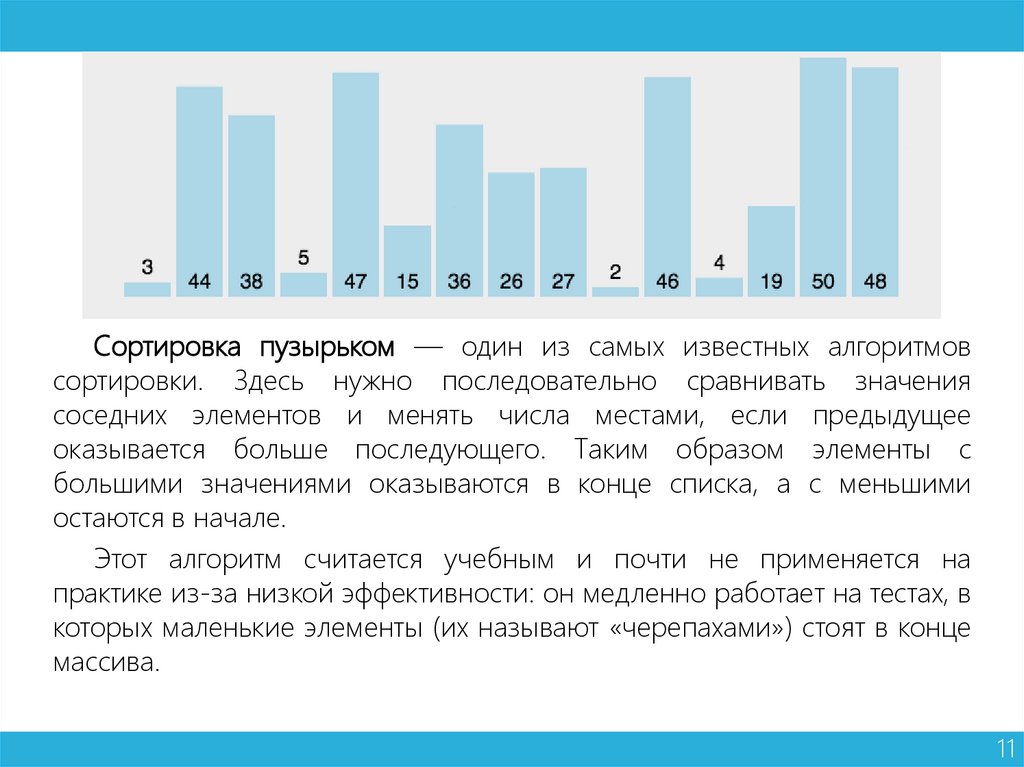
Сортировка пузырьком — один из самых известных алгоритмов
сортировки. Здесь нужно последовательно сравнивать значения
соседних элементов и менять числа местами, если предыдущее
оказывается больше последующего. Таким образом элементы с
большими значениями оказываются в конце списка, а с меньшими
остаются в начале.
Этот алгоритм считается учебным и почти не применяется на
практике из-за низкой эффективности: он медленно работает на тестах, в
которых маленькие элементы (их называют «черепахами») стоят в конце
массива.
11

12.

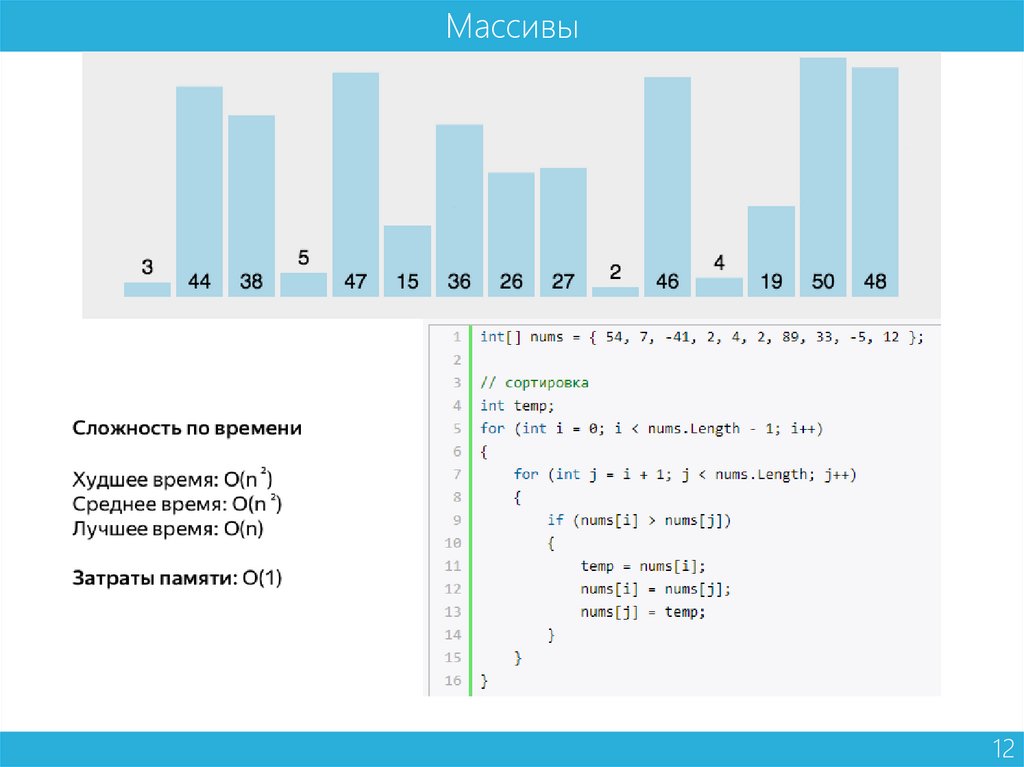
Массивы
12

13.

Шейкерная сортировка отличается от
пузырьковой тем, что она двунаправленная:
алгоритм перемещается не строго слева
направо, а сначала слева направо, затем
справа налево.
13

14.

Сортировка расчёской — улучшение
сортировки пузырьком. Её идея состоит в том,
чтобы «устранить» элементы с небольшими
значения в конце массива, которые
замедляют работу алгоритма. Если при
пузырьковой и шейкерной сортировках при
переборе массива сравниваются соседние
элементы, то при «расчёсывании» сначала
берётся достаточно большое расстояние
между сравниваемыми значениями, а потом
оно сужается вплоть до минимального.
Первоначальный разрыв нужно выбирать
не случайным образом, а с учётом
специальной
величины
—
фактора
уменьшения, оптимальное значение которого
равно 1,247. Сначала расстояние между
элементами будет равняться размеру массива,
поделённому
на
1,247;
на
каждом
последующем шаге расстояние будет снова
делиться на фактор уменьшения — и так до
окончания работы алгоритма.
14

15.

Быстрая сортировка. Этот алгоритм
состоит из трёх шагов. Сначала из массива
нужно выбрать один элемент — его
обычно называют опорным. Затем другие
элементы в массиве перераспределяют так,
чтобы
элементы
меньше
опорного
оказались до него, а большие или равные
— после. А дальше рекурсивно применяют
первые два шага к подмассивам справа и
слева от опорного значения.
Быструю сортировку изобрели в 1960
году для машинного перевода: тогда
словари хранились на магнитных лентах, а
сортировка слов обрабатываемого текста
позволяла получить переводы за один
прогон ленты, без перемотки назад.
15

16.

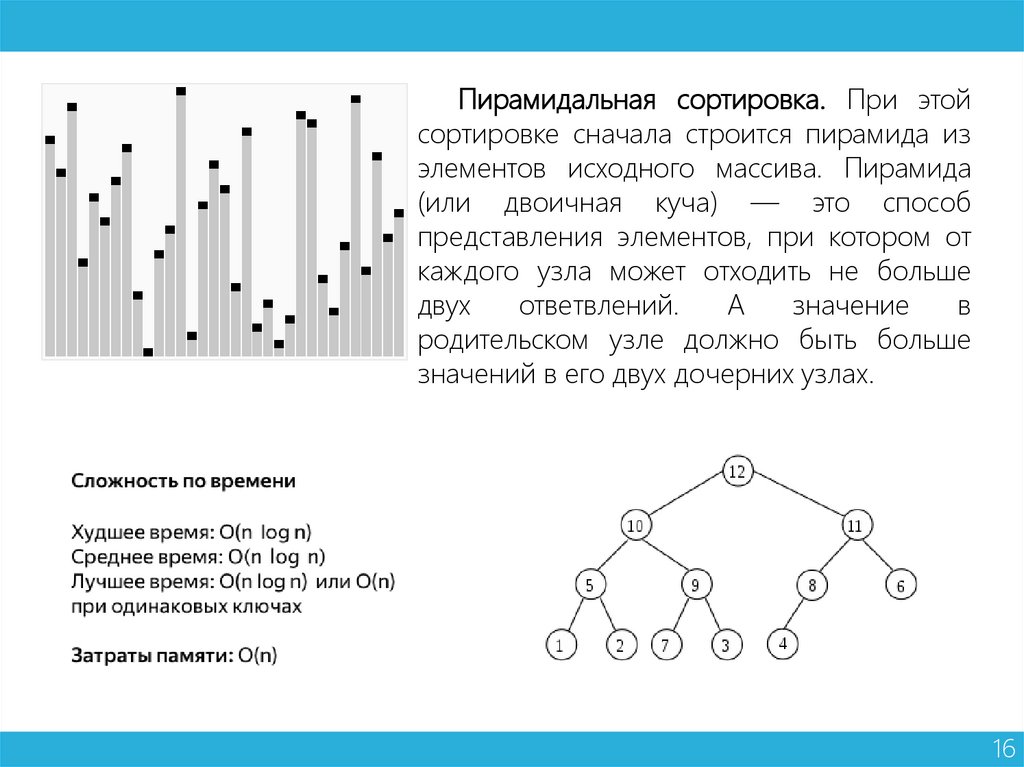
Пирамидальная сортировка. При этой
сортировке сначала строится пирамида из
элементов исходного массива. Пирамида
(или двоичная куча) — это способ
представления элементов, при котором от
каждого узла может отходить не больше
двух
ответвлений.
А
значение
в
родительском узле должно быть больше
значений в его двух дочерних узлах.
16

17.

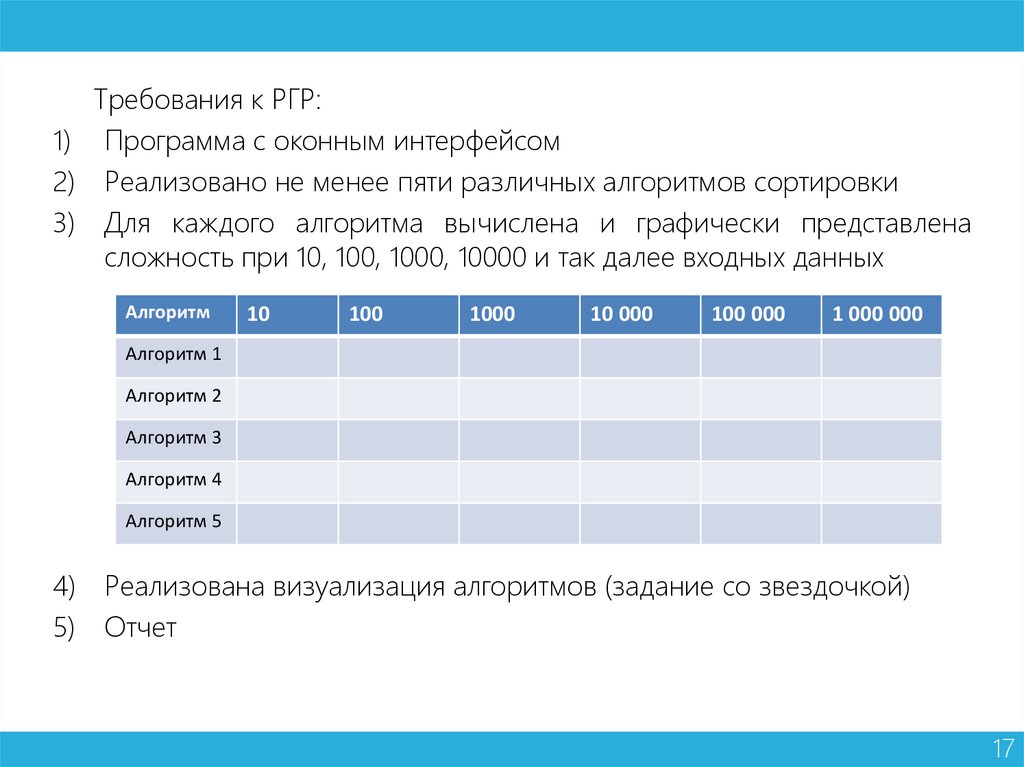
Требования к РГР:
1) Программа с оконным интерфейсом
2) Реализовано не менее пяти различных алгоритмов сортировки
3) Для каждого алгоритма вычислена и графически представлена
сложность при 10, 100, 1000, 10000 и так далее входных данных
Алгоритм
10
100
1000
10 000
100 000
1 000 000
Алгоритм 1
Алгоритм 2
Алгоритм 3
Алгоритм 4
Алгоритм 5
4) Реализована визуализация алгоритмов (задание со звездочкой)
5) Отчет
17