МО_4_сети

1. Методы оптимизации Тема «Оптимизация на сетях»

Граецкая Оксана Владимировна, к.т.н., доцент
кафедры системного анализа и управления

2. Основные характеристики сети

Сетью называется конечный ориентированный граф без циклов и
петель, с 2-мя выделенными вершинами, одна из которых называется
истоком (входом) I, а другая – стоком (выходом) S.
В дальнейшем будем предполагать, что в любой сети с вершинами i, j
наряду с дугой (i, j), соединяющей вершины i – начало, j – конец
присутствует дуга (j, i) (j – начало, i – конец).
Считаем, что по ребрам сети из истока I в сток S направляется некоторое
«вещество» (груз, ресурс, информация,…).
Максимальное количество вещества rij, которое можно пропустить за
единицу времени по ребру (i, j) из вершины i в вершину j называется
пропускной способностью ребра (i, j).
В общем случае rij ≠ rji.
Если вершины в сети не соединены ребром, то пропускная способность
между ними равна нулю. Так как в сети отсутствуют петли, то rii=0.
Обычно на сети пропускные способности ребер (i, j) и (j, i) указывают в
виде пары (rij,rji), при этом на сети можно изобразить только одно ребро,
тогда первое число соответствует пропускной способности в
направлении стрелки.
(rij,rji)
i
j
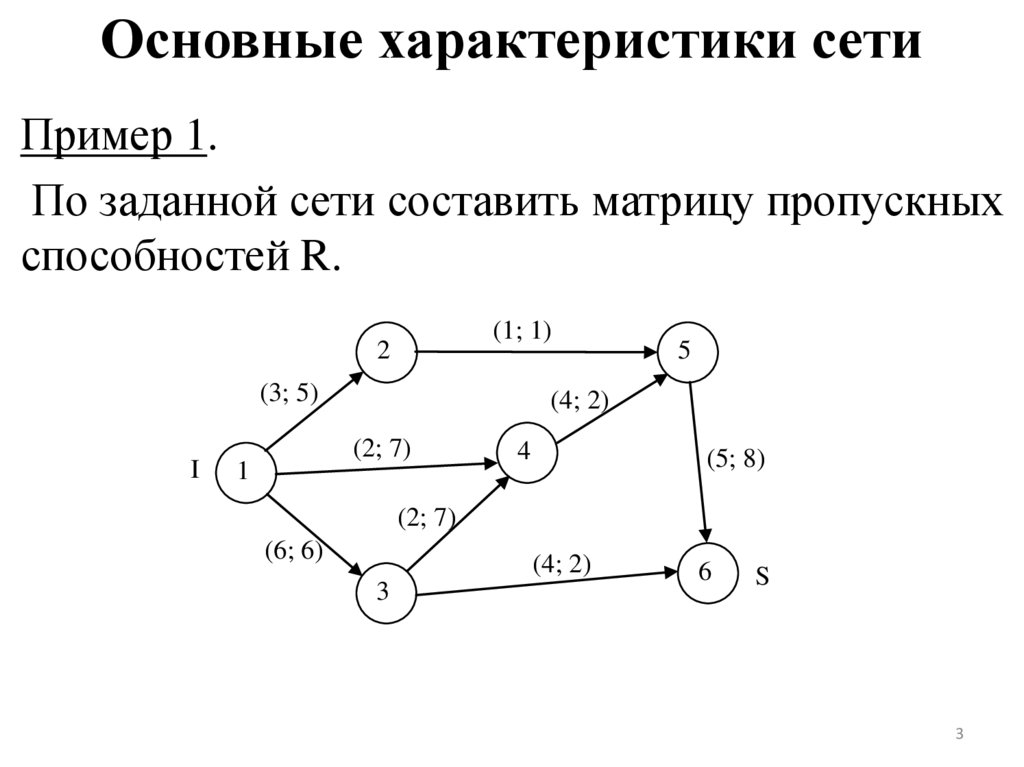
Пропускные способности задаются в виде матрицы R=(rij) порядка nxn.
2

3. Основные характеристики сети

Пример 1.
По заданной сети составить матрицу пропускных
способностей R.
(1; 1)
2
(3; 5)
I
(4; 2)
(2; 7)
1
5
4
(5; 8)
(2; 7)
(6; 6)
(4; 2)
3
6
S
3

4. Основные характеристики сети

Количество вещества xij, проходящее через ребро (i, j) от i к j в единицу
времени, называется потоком по ребру (i, j).
Так как в графе нет петель, то xii=0, I ①.
Если по ребру (i, j) прошло количество вещества xij из i в j, то это равносильно
тому, что из j в i прошло количество вещества xji=-xij, i, j ②.
Если поток xij по ребру (i, j) меньше пропускной способности ребра (xij<rij), то
ребро (i, j) называется ненасыщенным.
Если xij=rij, то ребро называется насыщенным.
Во всех случаях xij≤rij, i, j ③.
Множество X={xij} потоков по всем ребрам сети называется потом по сети или
просто потоком.
Для всех вершин сети, кроме истока I и стока S, количество вещества,
поступающего в эту вершину равно количеству вещества, вытекающего из нее:
, i, j ≠ I, S ④
Из ④ получаем, что общее количество вещества, вытекающего из истока I
равно общему количеству вещества, поступающему в сток S:
⑤, где суммирование ведется по таким j, которые соответствуют
ребрам (i,j), выходящим из истока I и таким i, которые соответствуют ребрам
(i,s), входящим в сток S.
Линейная функция f вида ⑤ называется мощностью потока на сети.
Любой путь в сети с началом в истоке I и концом в стоке S, называется
4
полным.

5. Основные характеристики сети

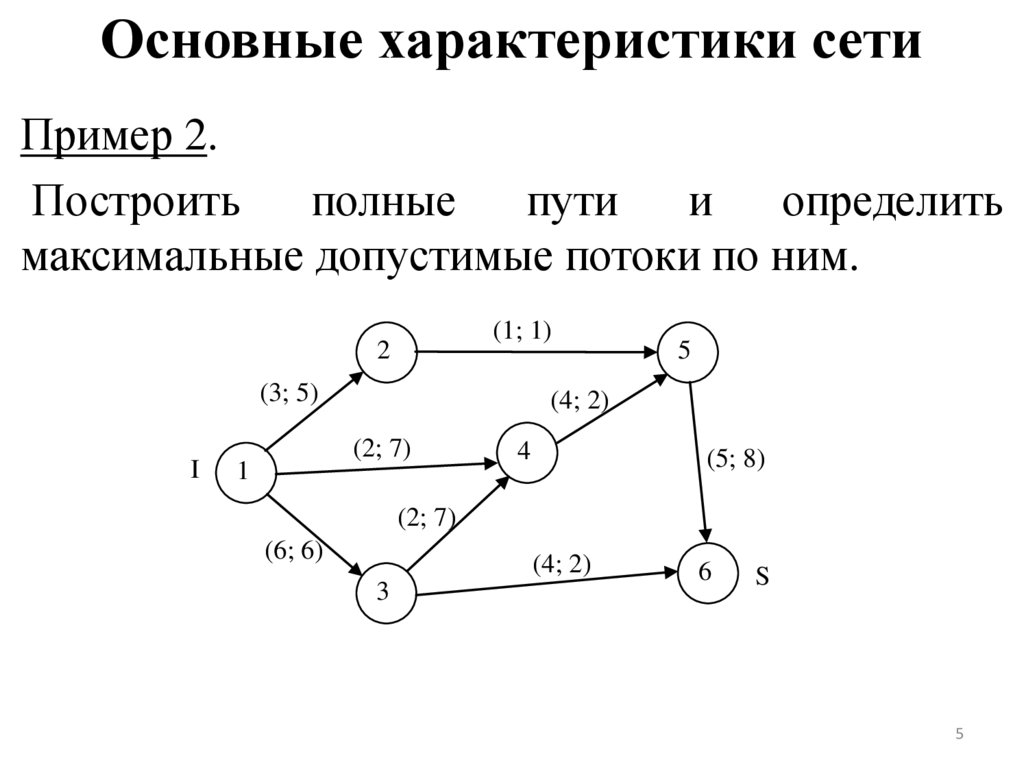
Пример 2.
Построить
полные
пути
и
определить
максимальные допустимые потоки по ним.
(1; 1)
2
(3; 5)
I
(4; 2)
(2; 7)
1
5
4
(5; 8)
(2; 7)
(6; 6)
(4; 2)
3
6
S
5

6. Разрез на сети. Теорема Форда-Фолкерсона

Пусть дана сеть. Разобьем множество всех вершин сети на два
подмножества A и B так, что I A, I B и S B, S A. В этом
случае говорят, что на сети выполнен разрез, отсекающий исток
I от стока S. При выполненном разбиении в сети окажутся
ребра (i, j), конечные вершины которых i и j попадут в разные
множества A и B.
Множество ребер (i, j), связывающих вершины, принадлежащие
разным множествам А и В, называется разрезом на сети и
обозначается А/В.
Величина R(А/В), равная сумме пропускных способностей всех
ребер разреза А/В, называется пропускной способностью
разреза А/В.
⑥
Пусть на сети задан поток X={xij} и некоторый разрез А/В.
Величина
⑦, равная сумме потоков по всем
ребрам разреза А/В, называется потоком через разрез А/В.
С учетом ③ получаем
⑧.
6

7. Разрез на сети. Теорема Форда-Фолкерсона

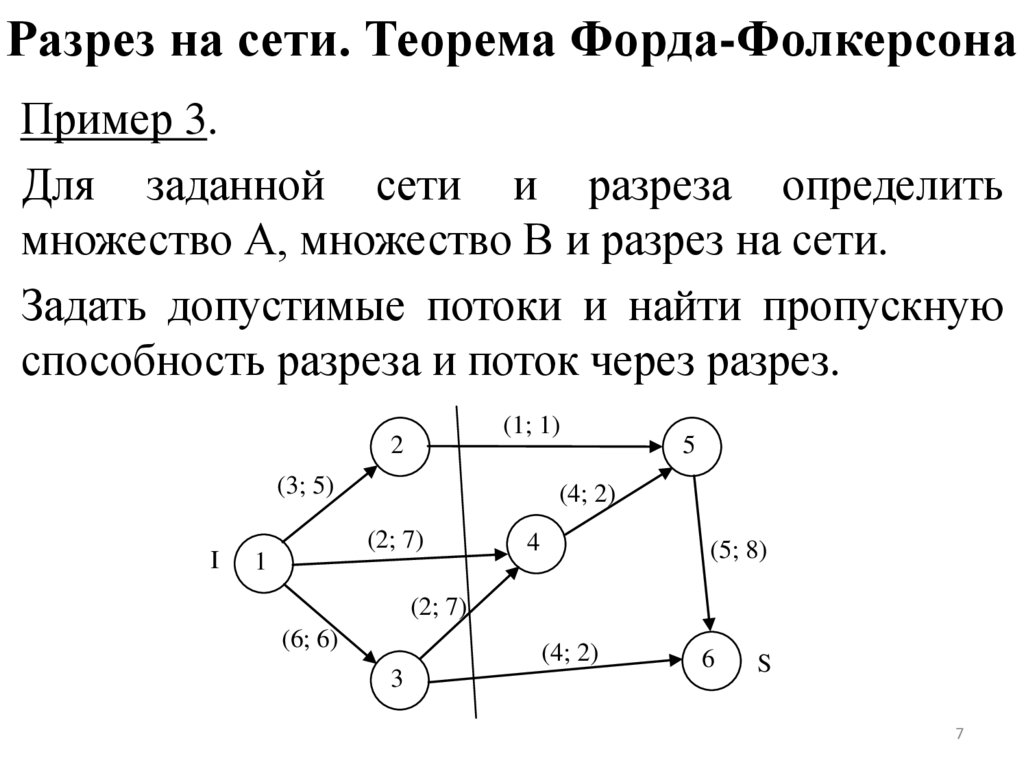
Пример 3.
Для заданной сети и разреза определить
множество А, множество В и разрез на сети.
Задать допустимые потоки и найти пропускную
способность разреза и поток через разрез.
(1; 1)
2
(3; 5)
I
(4; 2)
(2; 7)
1
5
4
(5; 8)
(2; 7)
(6; 6)
(4; 2)
3
6
S
7

8. Разрез на сети. Теорема Форда-Фолкерсона

Теорема Форда-Фолкерсона.
На любой сети максимальная величина потока от
истока I в сток S равна минимальной пропускной
способности всех возможных разрезов A/B,
отделяющих исток от стока (I A,I B,S B,S A).
8

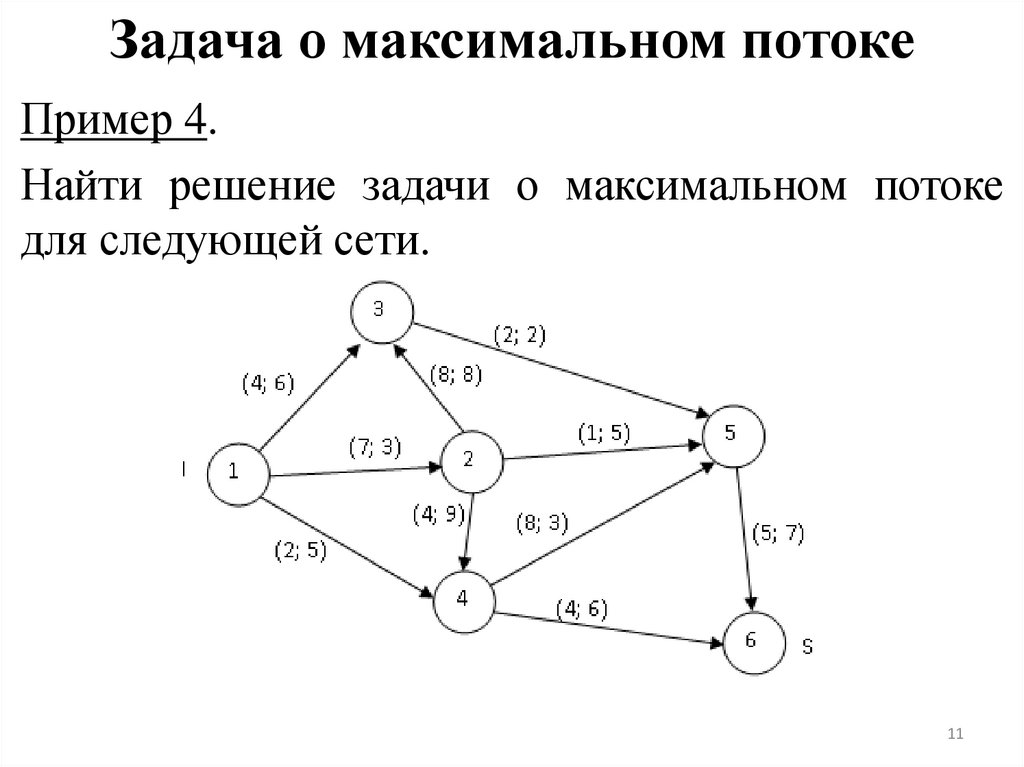
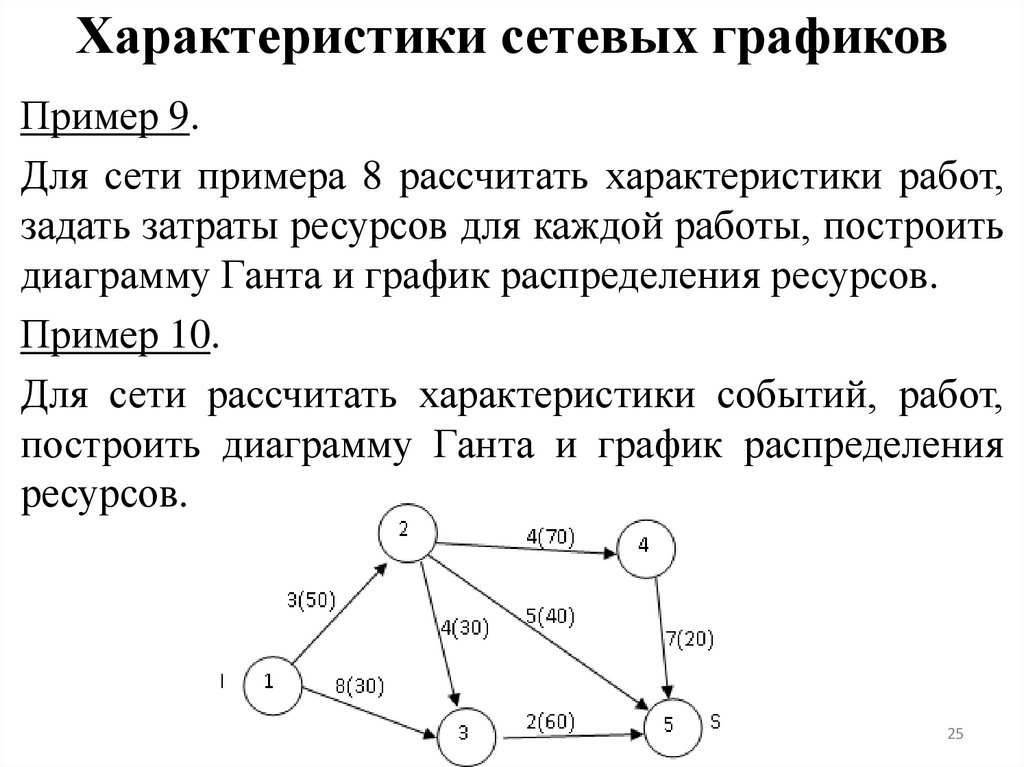
9. Задача о максимальном потоке

Найти такое распределение потока X*={xij*}, при котором мощность потока
(количество вещества, передаваемого из истока I в сток S) окажется
максимальной, то есть необходимо найти такое Х*, при котором достигается
максимум ⑤ при ограничениях ①-④.
Пусть X={xij} – допустимый поток сети.
Разобьем множество вершин на два подмножества А и В.
• А: Исток I и все вершины, достижимые из I хотя бы по одному пути,
образованному ненасыщенными ребрами.
• В: все остальные вершины.
Возможны два случая:
1) S A (S B). Тогда существует путь из I в S, состоящий из ненасыщенных
ребер. По этому пути можно пропустить дополнительный поток ∆=
min(