funktsii-mnogikh-peremennykh

1. Функции многих переменных

Лутковская Е.А.

2. n-мерное Евклидово пространство

3. Расстояние в Евклидовом пространстве

4. n-мерный шар

5. n-мерный параллелепипед

6. Окрестность точки

7. Функция многих переменных

8. Примеры

9. График функции многих переменных

10. Пример

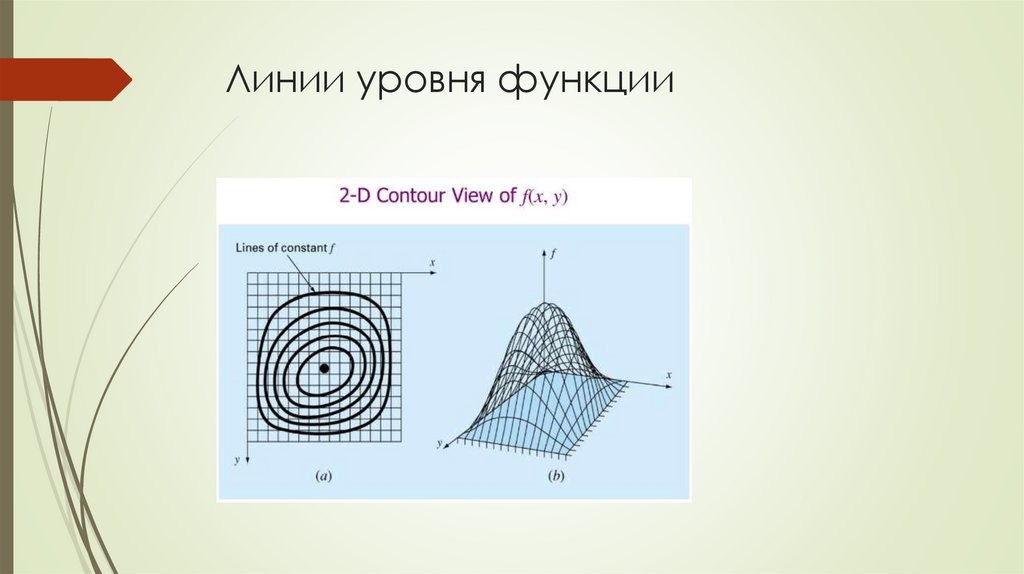
11. Поверхность и линия уровня

12. Линии уровня функции

13. Пример.

14. Линейная и квадратичная функция

15. Производственная функция Кобба-Дугласа

16. Замечание

17. Предел функции многих переменных

18. Непрерывность функции многих переменных

19. Частное приращение функции

20. Полное приращение функции

21. Частная производная

22. Пример

23. Частные производные второго и высших порядков

24. Примеры.

25. Теорема.

26. Экономический смысл частных производных

27. Дифференциал функции многих переменных

28. Применение дифференциала для приближенных вычислений

29. Градиент функции

30. Экстремумы функции многих переменных

31. Седловая точка

32. Достаточное условие экстремума

33. Схема исследования функции 2х переменных на экстремум

34. Пример.

35. Применение в экономике.

Рассмотрим случай, когда используются два ресурса: труд и капитал.
Равновесие производителя — ситуация, когда производственная функция достигает
максимального значения
при заданных издержках С, цене труда w и цене капитала г, т.е. при выполнении бюджетного
ограничения
где L и К— затраты труда и капитала соответственно. Набор затрат ресурсов, при котором
производитель достигает равновесия, называют равновесным.
В качестве производственной функции чаще всего используется

36. Равновесие производителя

Решив задачу определения равновесия производителя методом Лагранжа,
получим несколько тождественных условий равновесия.
1. В состоянии равновесия производителя предельные продукты ресурсов,
деленные на соответствующие цены, равны между собой:
Из данного равенства следует, что в состоянии равновесия производителю
безразлично, на какой из двух ресурсов тратить дополнительный рубль. В обоих
случаях он получит одинаковый прирост выпуска продукта.
2. В состоянии равновесия производителя предельные продукты ресурсов
пропорциональны ценам соответствующих ресурсов:
3. В состоянии равновесия производителя предельная норма технологического
замещения равна отношению цен ресурсов:

37. Изокванта и изокоста

ИЗОКВАНТА — кривая, демонстрирующая различные варианты
комбинаций факторов производства, которые могут быть использованы
для выпуска данного объема продукта. Изокванты иначе называют
кривыми равных продуктов, или линиями равного выпуска.
ИЗОКОСТА — линия, демонстрирующая комбинации факторов
производства, которые можно купить за одинаковую общую сумму
денег. Изокосту иначе называют линией равных издержек. Изокосты
являются параллельными прямыми, поскольку допускается, что фирма
может приобрести любое желаемое количество факторов
производства по неизменным ценам.
В состоянии равновесия производителя изокоста касается некоторой
изокванты производственной функции.

38. Пример.

Пример 8. Издержки производителя равны 36, цены труда и капитала равны 3 и 6
соответственно. Производственная функция задана формулой
Определим равновесный набор и максимальный выпуск. Для этого найдем функции
предельного продукта. Дифференцируя заданную функцию последовательно по обоим
аргументам, получим
Предельная норма технологического замещения равна отношению предельных продуктов
труда и капитала:
Согласно условию равновесия (форма записи № 3), предельная норма технологического
замещения равна отношению цен ресурсов:
Данное равенство задает соотношение между затратами ресурсов в равновесном
наборе при любой величине издержек производителя. Для определения конкретной точки
равновесия запишем бюджетное ограничение производителя для нашего случая:
Подставляя в данное равенство соотношение затрат ресурсов в равновесном наборе,
получим уравнение относительно затрат капитала:
Итак, равновесным является набор (8, 2), максимальный выпуск равен 2 х 8 х 2^0,5 = 22,6.
Предельная норма технологического замещения для равновесного набора равна 2x2:8 =
0,5, т.е. она равна отношению цен ресурсов 3 : 6. Как мы убедились, условие равновесия

39. 3D графики в онлайн-калькуляторах

3D графики в онлайнкалькуляторах

40. Desmos 3D graphic calculator

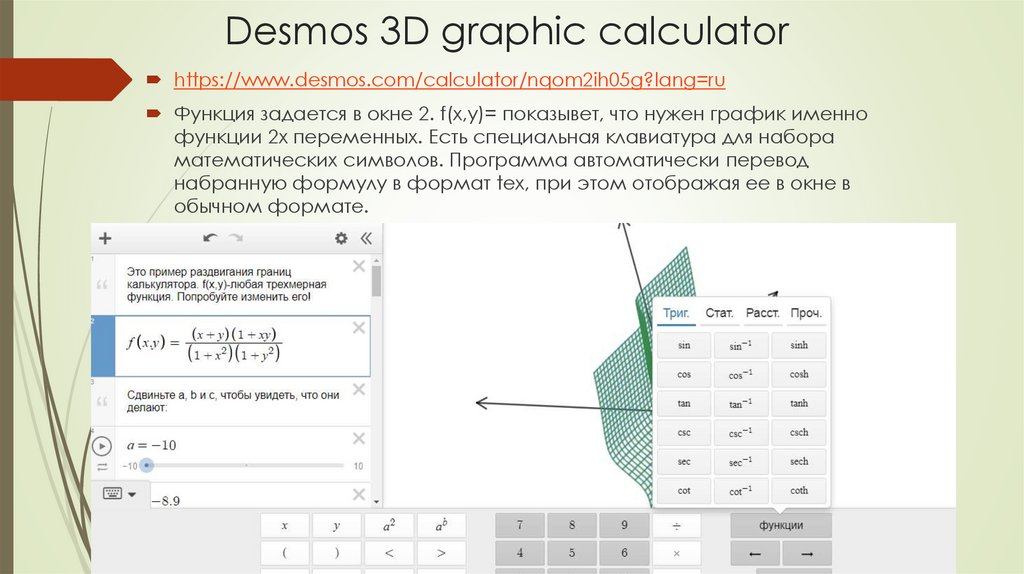
https://www.desmos.com/calculator/nqom2ih05g?lang=ru
Функция задается в окне 2. f(x,y)= показывет, что нужен график именно
функции 2х переменных. Есть специальная клавиатура для набора
математических символов. Программа автоматически перевод
набранную формулу в формат tex, при этом отображая ее в окне в
обычном формате.

41.

Бегунки a,b,c позволяют вращать график, при этом ось z не
обязательно направлена вверх.
Нет возможности визуализировать линии уровня функции.

42. Wolfram alpha

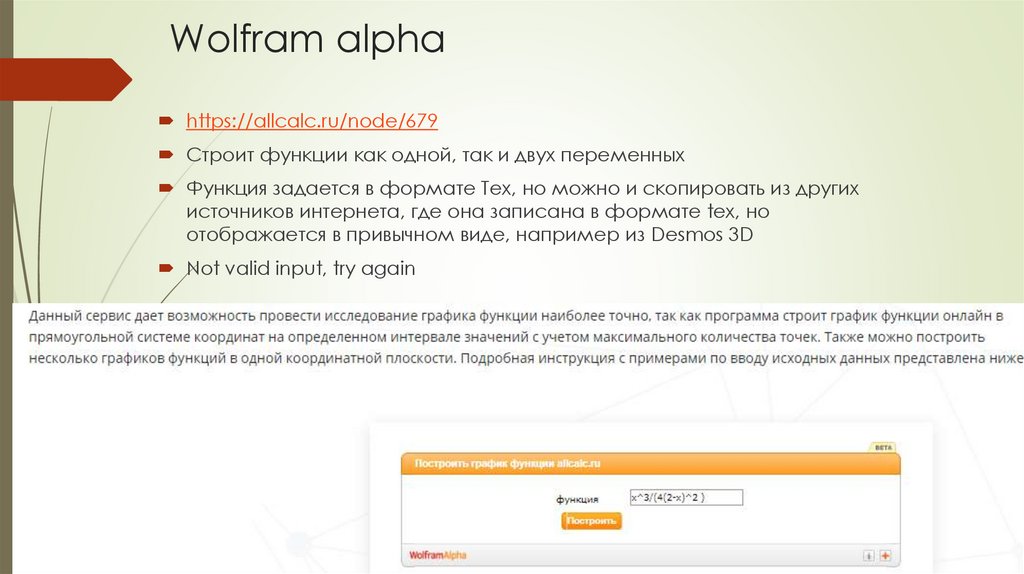
https://allcalc.ru/node/679
Строит функции как одной, так и двух переменных
Функция задается в формате Tex, но можно и скопировать из других
источников интернета, где она записана в формате tex, но
отображается в привычном виде, например из Desmos 3D
Not valid input, try again

43. Wolfram alpha

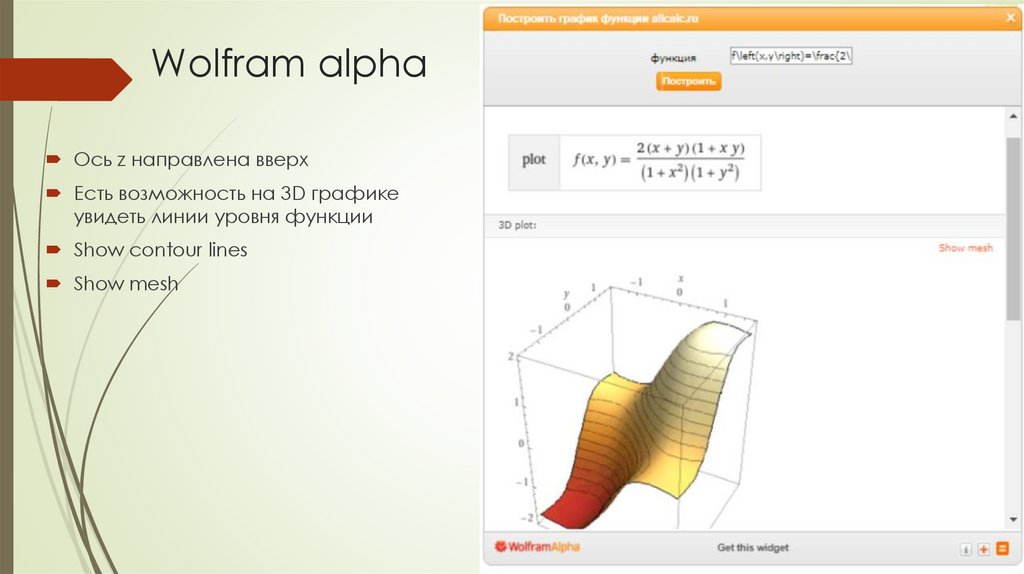
Ось z направлена вверх
Есть возможность на 3D графике
увидеть линии уровня функции
Show contour lines
Show mesh

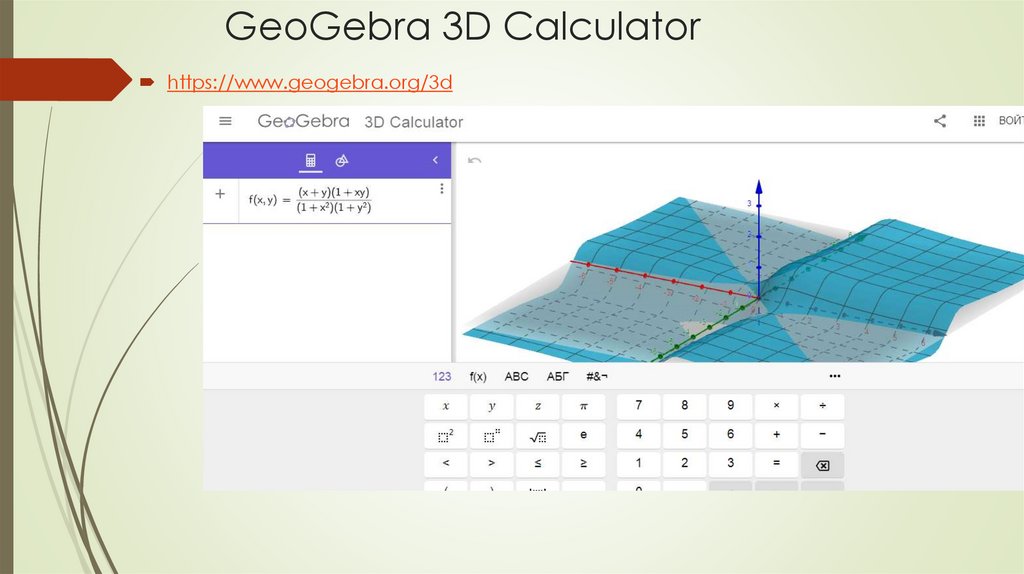
44. GeoGebra 3D Calculator

https://www.geogebra.org/3d

45. GeoGebra 3D Calculator

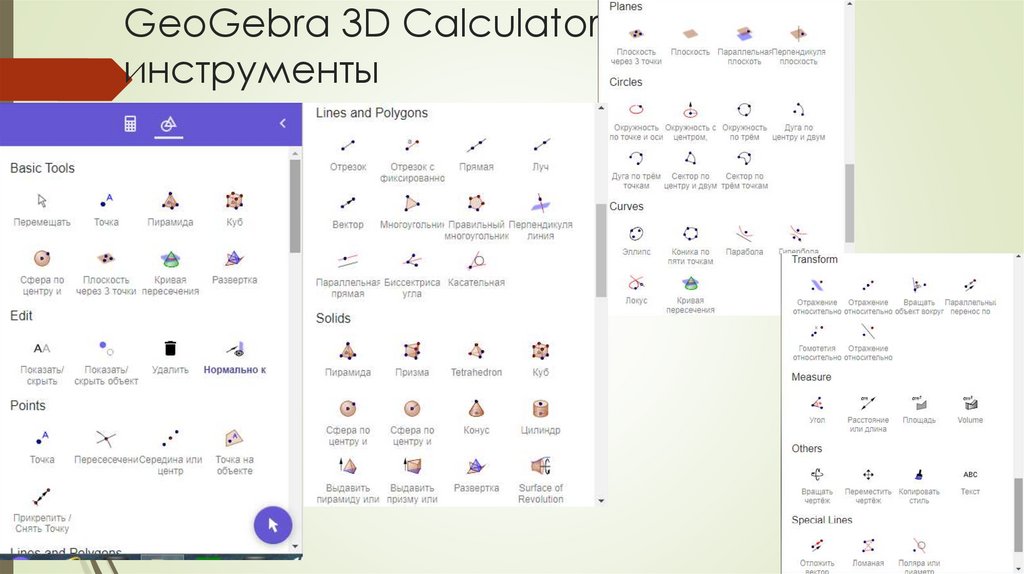
Можно вращать в любую сторону, двигая за стрелочки

46. GeoGebra 3D Calculator инструменты

47. Решение задачи

Критические точки: (1,1), (1,-1), (-1,1), (-1,-1)
(1,1) – точка минимума
(-1,-1) – точка максимума
(1,-1) и (-1,1) – седловые точки

48. Математические пакеты

Mathcad
Mathlab
Maxima
CalcPlot3D
Python

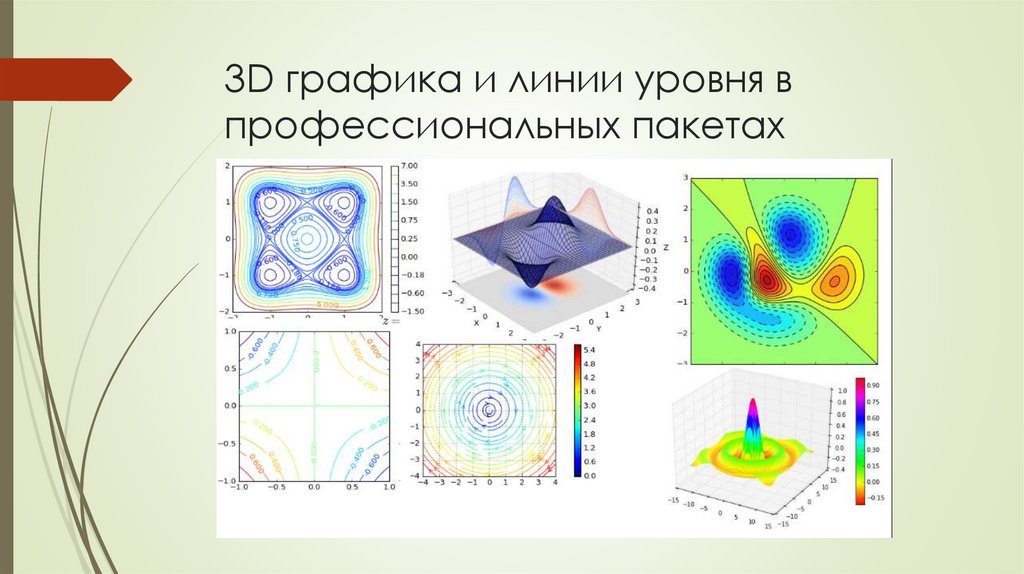
49. 3D графика и линии уровня в профессиональных пакетах

50.

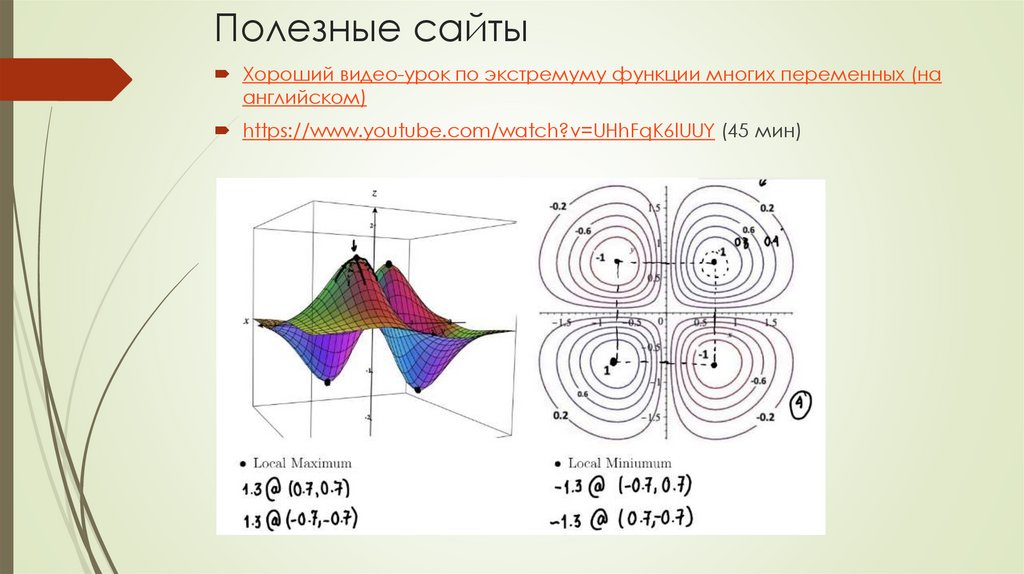
51. Полезные сайты

Хороший видео-урок по экстремуму функции многих переменных (на
английском)
https://www.youtube.com/watch?v=UHhFqK6lUUY (45 мин)

52. Литература

Высшая математика для экономистов: учебник для студентов вузов,
обучающихся по экономическим специальностям / Н. Ш. Кремер и
др.; под ред. проф. Н. Ш. Кремера. - 3-е изд. - м. : юнити-дана, 2012. 479 с. - (Серия «Золотой фонд российских
учебников»). https://drive.google.com/file/d/1LBUJ1fiv12lcZJ5xZz9Gpm6D3
VS9dKgA/view
Клюшин В. Л. Высшая математика для экономистов: Учеб. пособие. —
М.: ИНФРА-М, 2009. — 448 с. — (Учебники РУДН).
https://www.studmed.ru/view/klyushin-vl-vysshaya-matematika-dlyaekonomistov_8dcc8cf0f70.html
https://studme.org/128674/ekonomika/ravnovesie_proizvoditelya
https://studopedia.ru/4_16274_izokvanta-i-izokosta-ravnovesieproizvoditelya-otdacha-ot-masshtaba.html