Лекция №5. Основные информационные процессы

1. ОСНОВНЫЕ ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ И ИХ РЕАЛИЗАЦИЯ

Принципы обработки информации компьютером. Арифметические
и логические основы работы компьютера.

2. Алгебра логики (булева алгебра)

• это раздел математики, возникший в XIX веке благодаря усилиям
английского математика Дж. Буля. Поначалу булева алгебра не имела
никакого практического значения. Однако уже в XX веке ее положения
нашли применение в разработке различных электронных схем. Законы и
аппарат алгебры логики стали использоваться при проектировании
различных частей компьютеров (память, процессор).
• Алгебра логики оперирует с высказываниями. Под высказыванием
понимают повествовательное предложение, относительно которого имеет
смысл говорить, истинно оно или ложно. Над высказываниями можно
производить определенные логические операции, в результате которых
получаются новые высказывания. Наиболее часто используются
логические операции, выражаемые словами «не», «и», «или».
• Логические операции удобно описывать так называемыми таблицами
истинности, в которых отражают результаты вычислений сложных
высказываний при различных значениях исходных простых
высказываний. Простые высказывания обозначаются переменными
(например, A и B).

3. Конъюнкция (логическое умножение)

• Сложное высказывание А & В истинно только в том случае, когда
истинны оба входящих в него высказывания. Истинность такого
высказывания задается следующей таблицей:
• Обозначим 0 – ложь, 1 – истина

4. Дизъюнкция (логическое сложение)

• Сложное высказывание A
В истинно, если истинно хотя бы одно из
входящих в него высказываний. Таблица истинности для логической
суммы высказываний имеет вид:

5. Инверсия (логическое отрицание)

• Присоединение частицы НЕ (NOT) к данному высказыванию называется
операцией отрицания (инверсии). Она обозначается Ā (или ¬А)и
читается не А . Если высказывание А истинно, то В ложно, и наоборот.
Таблица истинности в этом случае имеет вид

6. Логические операции:

• Приоритет логических операций: если в выражении нет скобок,
сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», и
самая последняя – «импликация».

7. Алгоритм

• система точных и понятных предписаний (команд, инструкций,
директив) о содержании и последовательности выполнения конечного
числа действий, необходимых для решения любой задачи данного типа.
Как всякий объект, алгоритм имеет название (имя). Также алгоритм
имеет начало и конец.
• В качестве исполнителя алгоритмов можно рассматривать человека,
любые технические устройства, среди которых особое место занимает
компьютер. Компьютер может выполнять только точно определенные
операции, в отличии от человека, получившего команду и имеющего
возможность сориентироваться в ситуации.

8. Алгоритм обладает следующими свойствами.

• 1. Дискретность (от лат. discretus – разделенный, прерывистый)
указывает, что любой алгоритм должен состоять из конкретных
действий, следующих в определенном порядке.
• 2. Детерминированность (от лат. determinate – определенность,
точность) указывает, что любое действие алгоритма должно быть строго и
недвусмысленно определено в каждом случае.
• 3. Конечность определяет, что каждое действие в отдельности и
алгоритм в целом должны иметь возможность завершения.
• 4. Результативность требует, чтобы в алгоритме не было ошибок, т.е.
при точном исполнении всех команд процесс решения задачи должен
прекратиться за конечное число шагов и при этом должен быть получен
ответ.
• 5. Массовость заключается в возможности применения алгоритма к
целому классу однотипных задач, различающихся конкретными
значениями исходных данных (разработка в общем виде).

9. Способы описания алгоритмов

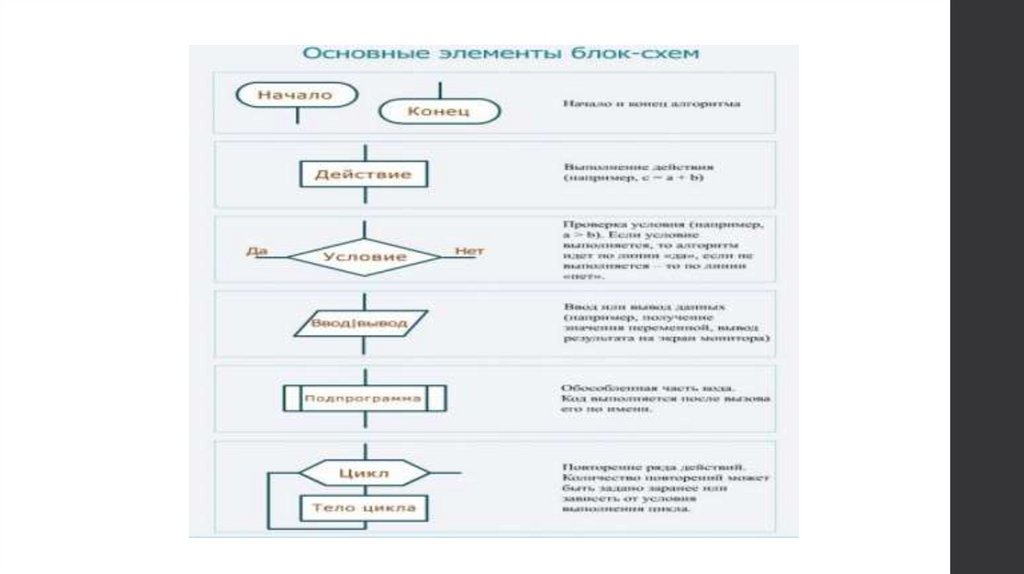
• словесный (на естественном языке);
• графический (с помощью стандартных графических
объектов (геометрических фигур) – блок-схемы);
• программный (с помощью языков программирования)

10.

11. Компьютер или ЭВМ

• – это универсальное техническое средство для автоматической обработки
информации. Аппаратное обеспечение компьютера – это все
устройства, входящие в его состав и обеспечивающие его исправную
работу.
• Несмотря на разнообразие компьютеров в современном мире, все они
строятся по единой принципиальной схеме, основанной на фундаменте
идеи программного управления Чарльза Бэббиджа(середина XIX в).
Эта идея была реализована при создании первой ЭВМ ENIAC в 1946
году коллективом учёных и инженеров под руководством известного
американского математика Джона фон Неймана.

12. Общие принципы построения:

1. Принцип программного управления. Из него следует, что программа
состоит из набора команд, которые выполняются процессором автоматически
друг за другом в определенной последовательности.
2. Принцип однородности памяти. Программы и данные хранятся в одной
и той же памяти. Поэтому компьютер не различает, что хранится в данной
ячейке памяти — число, текст или команда. Над командами можно
выполнять такие же действия, как и над данными. Это открывает целый ряд
возможностей. Например, программа в процессе своего выполнения
также может подвергаться переработке, что позволяет задавать в самой
программе правила получения некоторых ее частей (так в программе
организуется выполнение циклов и подпрограмм).
3. Принцип адресности. Структурно основная память состоит из
пронумерованных ячеек; процессору в произвольный момент времени
доступна любая ячейка. Отсюда следует возможность давать имена областям
памяти, так, чтобы к запомненным в них значениям можно было
впоследствии обращаться или менять их в процессе выполнения программ с
использованием присвоенных имен.

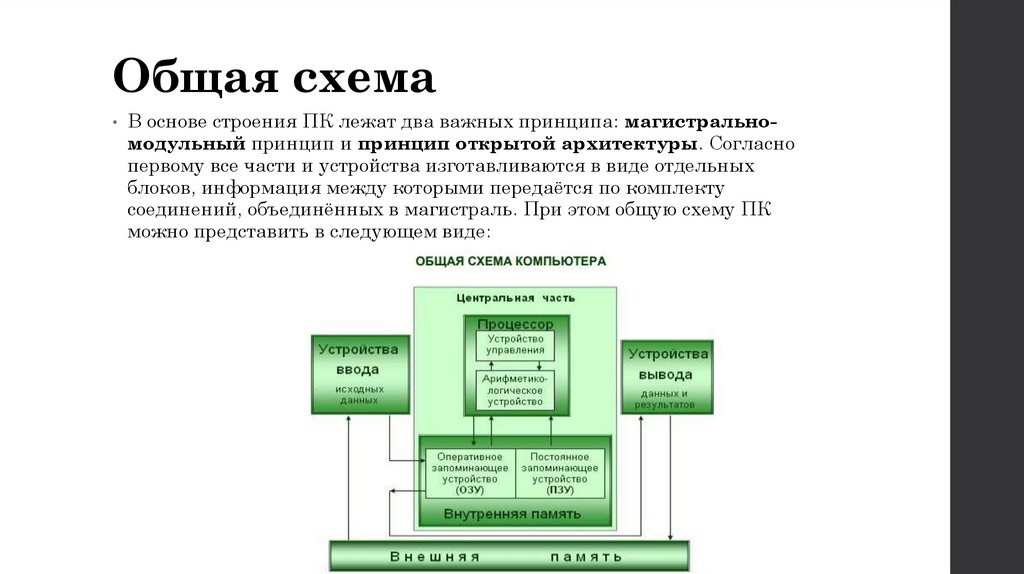
13. Общая схема

• В основе строения ПК лежат два важных принципа: магистрально-
модульный принцип и принцип открытой архитектуры. Согласно
первому все части и устройства изготавливаются в виде отдельных
блоков, информация между которыми передаётся по комплекту
соединений, объединённых в магистраль. При этом общую схему ПК
можно представить в следующем виде:

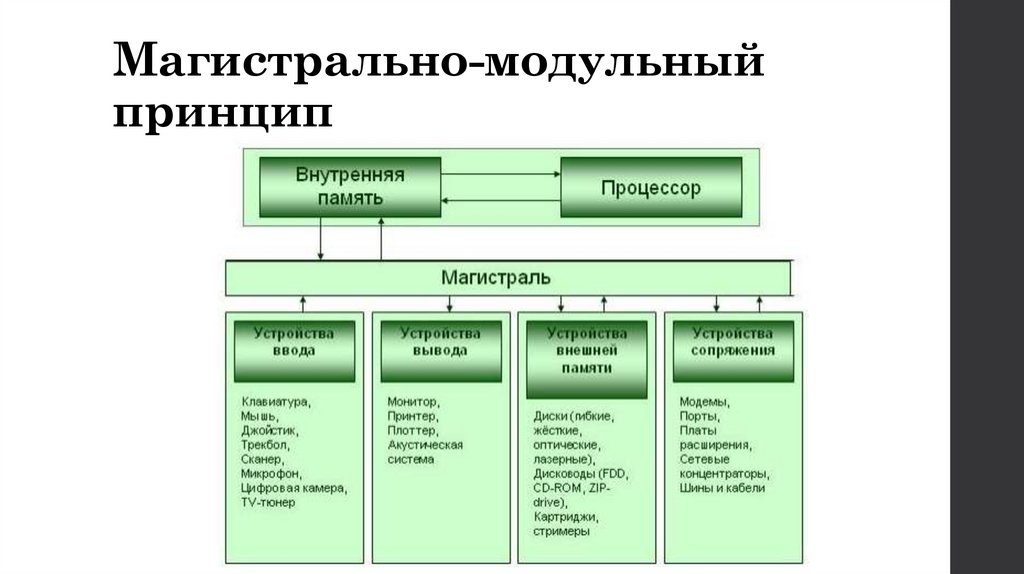
14. Магистрально-модульный принцип

• Идея: Компьютер строится из отдельных устройств (модулей),
которые подключаются к общей системе соединений –
магистрали.
• Магистраль: Это набор шин (шины данных, адреса и
управления), по которым передается информация между всеми
компонентами ПК.
• Преимущества: Обеспечивает гибкость в сборке, возможность
модернизации системы и масштабируемость

15. Магистрально-модульный принцип

16. Принцип открытой архитектуры

• Идея: Компьютер собирается из независимых частей,
изготовленных разными производителями, что делает их
доступными для всех желающих, подобно детскому конструктору.
• Цель: Позволяет пользователям самостоятельно комплектовать
ПК и производить его модернизацию, устанавливая новые платы
расширения или заменяя компоненты.
• Исторический пример: Компьютеры IBM PC стали одним из
первых и ярких примеров такой архитектуры.

17. Основные информационные процессы

• Информационный процесс — процесс получения, создания, сбора,
обработки, накопления, хранения, поиска, распространения и
использования информации.
• В целом, любые действия, выполняемые с информацией,
называются информационными процессами.
• Существует четыре типа информационных процессов:
• 1. Получение
• 2. Хранение
• 3. Обработка
• 4. Передача

18. Информационные процессы:

• Хранение. В аналоговой форме (бумага, камень, береста, граммофонная
пластинка, магнитофонная лента…)
• В цифровой форме (память ПК, флешки, винчестеры, CD, DVD, …)
• Обработка. кодирование – изменение формы, запись в некоторой
знаковой системе (в виде кода)
• поиск
• сортировка – расстановка элементов списка в заданном порядке
• Передача. Обмен информацией – всегда двусторонний процесс: есть
источник и приёмник информации.
• Большая часть воспринимается в образной форме. Информация,
воспринимаемая человеком в речевой или письменной форме,
называется знаковой (символьной).

19. Язык 

Язык
• – это знаковая система представления информации. Обмен
информацией может происходить как при непосредственном общении
между людьми, так и с помощью технических средств связи: телефона,
радио, телевидения, компьютерных сетей и т.д.
• Отметим, что без помощи технических средств люди способны
обмениваться информацией только в знаковой форме (голосом, жестами,
мимикой) и на небольшом расстоянии.

20. Человеку почти непрерывно приходится заниматься обработкой информации

• получение новой информации из данной путем вычислений или
логических рассуждений (решение математической задачи);
• изменение формы представления информации (перевод текста с одного
языка на другой);
• поиск информации в информационном массиве (поиск номера телефона
в телефонной книге);
• сортировка информации (упорядочение списка учеников класса в
алфавитном порядке).

21. Задания:

• 1. Таблица истинности "И" (∧)
Заполните таблицу для выражения: F = A ∧ B
• 2. Таблица истинности "ИЛИ" (∨)
Заполните таблицу для выражения: F = A ∨ B
• 3. Отрицание
Найдите значения ¬A для:
• A = 1 → ¬A = ?
• A = 0 → ¬A = ?
• 4. Простое выражение
Вычислите значение выражения при A=1, B=0:
F = A ∧ (B ∨ 1)
• 5. Упрощение
Упростите выражение: F = A ∨ (A ∧ B)

22. Задания:

• 6. Законы Де Моргана (простой вариант)
Упростите: F = ¬(A ∧ B)
• 7. Импликация
Вычислите A → B при:
• A=1, B=1 → ?
• A=1, B=0 → ?
• 8. Логическое тождество
Проверьте, является ли тождеством: A ∨ ¬A = 1
• 9. Подстановка значений
Найдите F при A=0, B=1: F = ¬A ∧ B
• 10. Составление выражения
Запишите логическое выражение для:
"Я пойду гулять, если будет хорошая погода и нет дождя"
(В = хорошая погода, D = дождь, G = гулять)

23.

Задание № 1
Задание № 2
A|B|F
0|0|0
0|1|0
1|0|0
1|1|1
A|B|F
0|0|0
0|1|1
1|0|1
1|1|1
3. Отрицание:
A = 1 → ¬A = 0
A = 0 → ¬A = 1
4. Вычисление:
A=1, B=0: F = 1 ∧ (0 ∨ 1) = 1 ∧ 1 = 1
5. Упрощение:
F = A ∨ (A ∧ B) = A
6. Законы Де Моргана:
F = ¬(A ∧ B) = ¬A ∨ ¬B
7. Импликация:
A=1, B=1 → 1
A=1, B=0 → 0
8. Логическое тождество:
A ∨ ¬A = 1 - да, является тождеством
9. Подстановка значений:
A=0, B=1: F = ¬0 ∧ 1 = 1 ∧ 1 = 1
10. Составление выражения:
G = B ∧ ¬D