9.86M

Чемпионат по МГ 1 тур старшая лига

1.

XIXIОбластной
Чемпионат
Областной Чемпионат
командных игр-конкурсов
игр-конкурсов
командных
математической грамотности
попо
математической
грамотности
для обучающихся Омской области
для обучающихся Омской области
Старшая лига
Старшая лига
Первый тур
Первый тур

2.

XI Областной Чемпионат командных игр-конкурсов по математической грамотности для обучающихся Омской области
Правила игры
Каждый тур состоит из 9 заданий, разных по степени сложности
и формату ответа.
Команды получают каждое задание отдельно (по одному) и решают
в строго отведенное время. Ведущий поочередно зачитывает задания,
которые параллельно транслируются на экране. На обсуждение одного
задания ведущий дает 3 минуты. За 20 секунд до конца отведенного
времени звучит предупреждающий звуковой сигнал, и команды передают
членам счетной комиссии заполненный бланк с ответом.
По истечении 3-х минут ведущий объявляет «Стоп». После данного
сигнала ответы не принимаются.
Ведущий игры оглашает правильный ответ после сдачи
бланков ответов.

3.

Задание № 1
XI Областной Чемпионат командных игр-конкурсов
по математичеcкой грамотности. Старшая лига.
Саша летом отдыхает у дедушки в деревне Масловка. В субботу они
собираются съездить на велосипедах в село Захарово в магазин.
Из деревни Масловка в село Захарово можно проехать по прямой
лесной дорожке. Есть более длинный путь: по прямолинейному шоссе
через деревню Вёсенка до деревни Полянка, где нужно повернуть
под прямым углом направо на другое шоссе, ведущее в село Захарово.
Есть и третий маршрут: в деревне Вёсенка можно свернуть
на прямую тропинку в село Захарово, которая идет мимо пруда. Лесная
дорожка и тропинка образуют с шоссе прямоугольные треугольники.
По шоссе Саша с дедушкой едут со скоростью 20 км/ч, а по лесной
дорожке и тропинке – со скоростью 15 км/ч. На плане изображено
взаимное расположение населённых пунктов, сторона каждой клетки
равна 1 км.
Сколько минут затратят на дорогу из деревни Масловка в село
Захарово Саша с дедушкой, если они поедут по прямой лесной
дорожке?
Запишите решение и ответ.

4.

Задание № 2
XI Областной Чемпионат командных игр-конкурсов
по математичеcкой грамотности. Старшая лига.
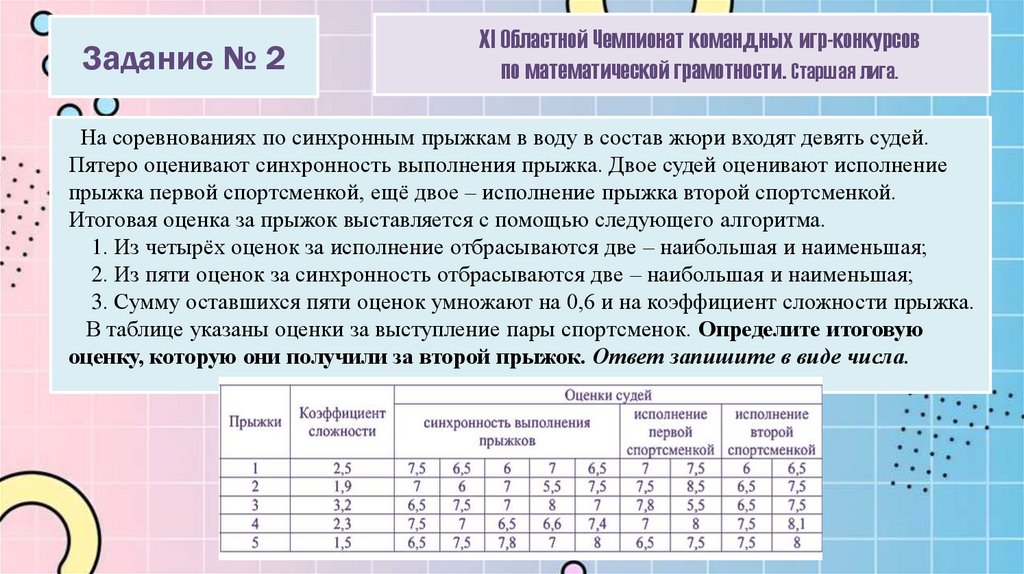
На соревнованиях по синхронным прыжкам в воду в состав жюри входят девять судей.
Пятеро оценивают синхронность выполнения прыжка. Двое судей оценивают исполнение
прыжка первой спортсменкой, ещё двое – исполнение прыжка второй спортсменкой.
Итоговая оценка за прыжок выставляется с помощью следующего алгоритма.
1. Из четырёх оценок за исполнение отбрасываются две – наибольшая и наименьшая;
2. Из пяти оценок за синхронность отбрасываются две – наибольшая и наименьшая;
3. Сумму оставшихся пяти оценок умножают на 0,6 и на коэффициент сложности прыжка.
В таблице указаны оценки за выступление пары спортсменок. Определите итоговую
оценку, которую они получили за второй прыжок. Ответ запишите в виде числа.

5.

Задание № 3
XI Областной Чемпионат командных игр-конкурсов
по математичеcкой грамотности. Старшая лига.
Рейтинг – основной показатель уровня шахматиста.
Шахматные партии бывают трёх видов (по времени):
классические, быстрые (рапид) и молниеносная игра
(блиц). По каждому виду проводятся турниры
и отдельно считается соответствующий рейтинг.
Рейтинговая система делит шахматистов на девять
классов: высший класс начинается с рейтинга в 2600,
в низшем классе – игроки с рейтингом 1200 и ниже.
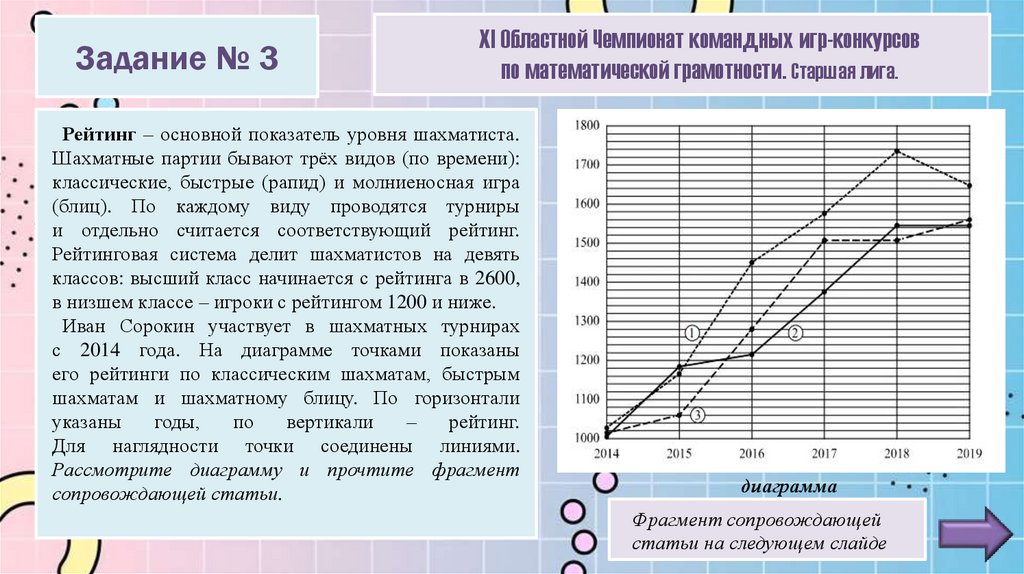
Иван Сорокин участвует в шахматных турнирах
с 2014 года. На диаграмме точками показаны
его рейтинги по классическим шахматам, быстрым
шахматам и шахматному блицу. По горизонтали
указаны
годы,
по
вертикали
–
рейтинг.
Для наглядности точки соединены линиями.
Рассмотрите диаграмму и прочтите фрагмент
сопровождающей статьи.
диаграмма
Фрагмент сопровождающей
статьи на следующем слайде

6.

Задание № 3
XI Областной Чемпионат командных игр-конкурсов
по математичеcкой грамотности. Старшая лига.
Наиболее успешно Иван выступает в классических шахматных
турнирах. За первые четыре года с начала занятий его рейтинг
поднялся более чем на 700 пунктов. И лишь в последний год
наблюдается небольшой спад рейтинга, что свидетельствует о том,
что занятия стали менее интенсивными.
Соревнованиям по быстрым шахматам и шахматному блицу Иван
уделяет меньше времени. Вероятно, поэтому его рейтинг по данным
дисциплинам ниже, чем по классическим шахматам, и находится около
отметки 1550. С 2017 по 2018 год Иван не играл в блиц-турнирах,
поэтому его рейтинг по шахматному блицу на протяжении этого
времени не менялся. А с 2018 по 2019 год Иван не участвовал
в турнирах по быстрым шахматам.
В одной секции с Иваном занимается Саша Воробьев. Наиболее
успешным в классических шахматах для Саши был 2016 год, когда его
рейтинг достиг своего максимального значения и равнялся 1530, что на
280 пунктов выше, чем в предыдущем году, и на 410 пунктов выше,
чем в 2014. Затем Саша стал играть менее интенсивно, и его рейтинг
стал снижаться. С 2016 по 2017 год он упал на 40 пунктов, а затем
каждый год из двух следующих лет падал ещё на 30 пунктов.
диаграмма
На основании прочитанного
определите, какому рейтингу
(по классическим шахматам,
быстрым
или
блиц)
соответствует график 3.

7.

Задание № 4
XI Областной Чемпионат командных игр-конкурсов
по математичеcкой грамотности. Старшая лига.
Стоимость билетов на поезда дальнего следования одного направления зависит
от нескольких факторов и меняется в течение года. В периоды, когда спрос наибольший,
цены выше, при понижении спроса в определённые месяцы железнодорожные билеты стоят
дешевле. Изменение цен по сравнению с базовым тарифом определяется с помощью
сезонных коэффициентов. Например, если обычная цена билета 1000 рублей, но действует
коэффициент 1,1, то билет будет стоить на 10 % дороже, то есть 1100 рублей. А если
действует коэффициент 0,9, то билет будет стоить 900 рублей. На графике показаны цены
на железнодорожные билеты в плацкартные вагоны в разные периоды 2024 года.
На
сколько
примерно
рублей
выросла цена билетов в плацкартные
вагоны 14 июня по сравнению
со второй половиной мая?
Ответ запишите в виде числа.

8.

Задание № 5
В колледже проводится конкурс
профессионального мастерства по
специальности «Повар». Конкурсное
задание состоит из теоретической и
практической части. Теоретическая
часть
включает
5
вопросов.
За каждый ответ участник получает
от 0 до 5 баллов.
Практическая часть заключается
в приготовлении горячего блюда.
Жюри оценивает практическую часть
баллами. Если участник допустил
нарушение
санитарных
норм
в
процессе
приготовления,
то начисляются штрафные баллы,
которые вычитаются из суммы баллов
за практическую часть.
XI Областной Чемпионат командных игр-конкурсов
по математичеcкой грамотности. Старшая лига.
Итоговый балл вычисляется по формуле:
Битог = 0,4∙Бтеор +(Бпракт ─ Бштраф).
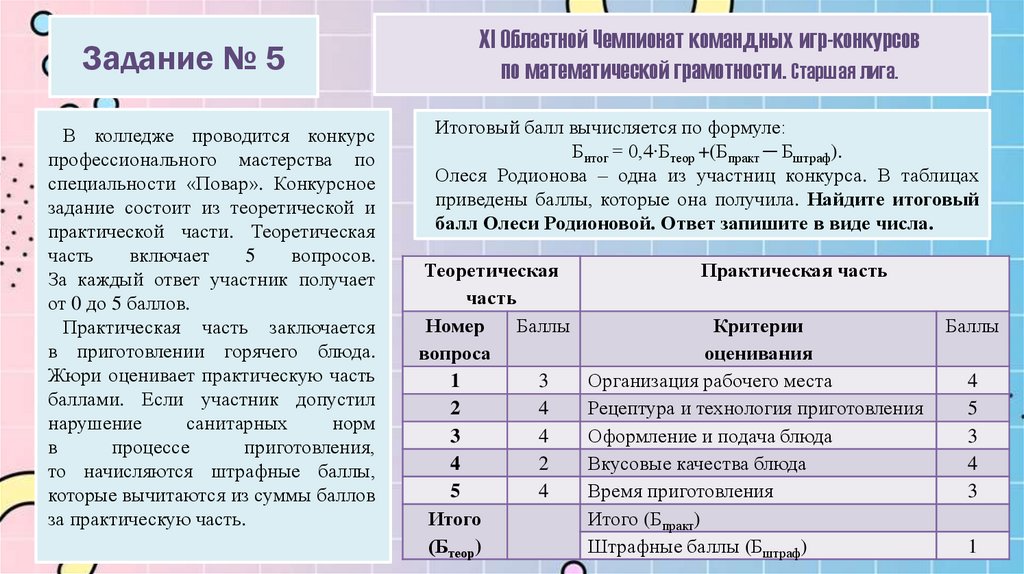
Олеся Родионова – одна из участниц конкурса. В таблицах
приведены баллы, которые она получила. Найдите итоговый
балл Олеси Родионовой. Ответ запишите в виде числа.
Теоретическая
часть
Номер
Баллы
вопроса
1
3
2
4
3
4
4
2
5
4
Итого
(Бтеор)
Практическая часть
Критерии
оценивания
Организация рабочего места
Рецептура и технология приготовления
Оформление и подача блюда
Вкусовые качества блюда
Время приготовления
Итого (Бпракт)
Штрафные баллы (Бштраф)
Баллы
4
5
3
4
3
1

9.

Задание № 6
XI Областной Чемпионат командных игр-конкурсов
по математичеcкой грамотности. Старшая лига.
Воспользуйтесь текстом «Классический бисквит». Выберите правильный ответ на вопрос задачи
и затем объясните свой ответ.
Задача. У домохозяйки осталось 200 граммов муки. Хватит ли ей этого количества муки
для изготовления классического бисквита диаметром 26 см?
Классический бисквит
Бисквит – это кондитерское тесто и кондитерский «хлеб»,
приготовленный из муки, сахара и яиц.
Расчёт
количества
ингредиентов
для
приготовления
классического бисквита идёт от одного яйца. На одно яйцо
необходимо взять:
─ 30 г сахара,
─ 25 г муки,
─ 6 г кукурузного крахмала,
─ 0,5 чайной ложки ванильного сахара,
─ ½ чайной ложки разрыхлителя.
На форму для выпекания, диаметром 18 см, необходимо взять
4 яйца. При увеличении диаметра формы на каждые 3 – 5 см
необходимо добавить еще одно яйцо.
Выберите правильный ответ:
1. Хватит муки;
2. Не хватит муки
Объясните свой ответ.

10.

Задание № 7
XI Областной Чемпионат командных игр-конкурсов
по математичеcкой грамотности. Старшая лига.
Зимние Олимпийские игры – это спортивные
соревнования, проходящие один раз в 4 года
под руководством Международного олимпийского комитета.
Зимние игры начали проводиться с 1974 года
как дополнение к летним играм. С 1924 по 1992 год зимние
Олимпийские игры проводились в те же годы, что и летние.
С 1994 года зимние Олимпийские игры проводятся
со сдвигом в 2 года относительно летних Олимпийских игр.
Первая зимняя Олимпиада прошла в 1924 году в Шамони
(Франция), в ней участвовали 293 спортсмена из 16 стран.
В 2018 году в XXIII Олимпийских играх в Пхёнчхане
(Южная Корея) участвовали уже 2922 спортсмена
из 92 стран.
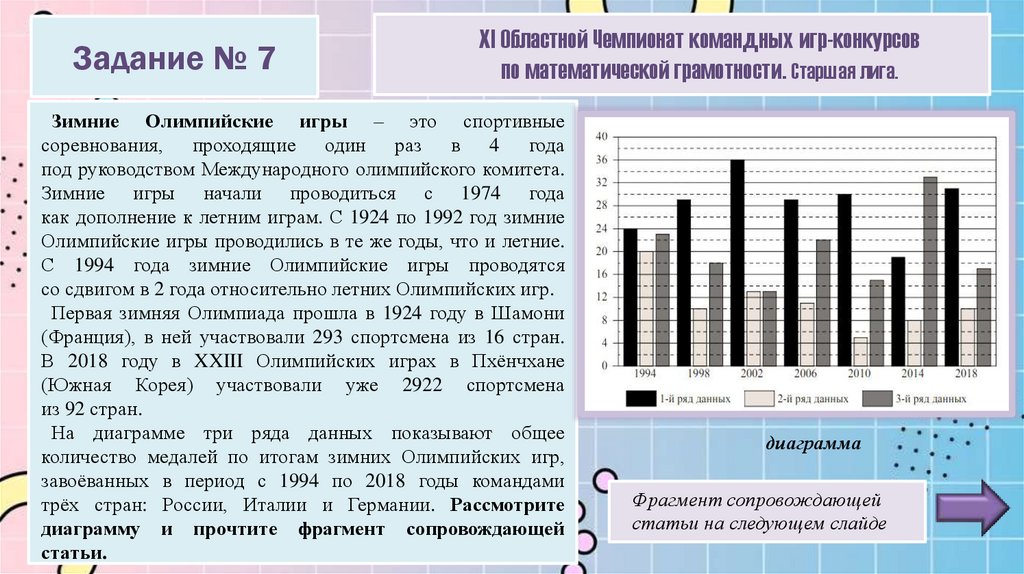
На диаграмме три ряда данных показывают общее
количество медалей по итогам зимних Олимпийских игр,
завоёванных в период с 1994 по 2018 годы командами
трёх стран: России, Италии и Германии. Рассмотрите
диаграмму и прочтите фрагмент сопровождающей
статьи.
диаграмма
Фрагмент сопровождающей
статьи на следующем слайде

11.

Задание № 7
XI Областной Чемпионат командных игр-конкурсов
по математичеcкой грамотности. Старшая лига.
Команда Германии принимает участие в зимних Олимпийских играх с 1928 года. В конце ХХ и начале ХХI века команда
Германии успешно выступает на зимней Олимпиаде. Наибольшее количество медалей – 36 – команда Германии завоевала
на Олимпиаде в Солт-Лейк-Сити (США) в 2002 году.
Российские спортсмены, начиная с 1994 года, завоевали на зимних Олимпийских играх 141 медаль. Самой успешной
для россиян оказалась Олимпиада – 2014, которая проходила в Сочи, где Россия положила в свою копилку 33 медали.
Италия принимала участие во всех соревнованиях зимних Олимпийских игр. Трижды она финишировала в пятёрке лучших
команд по количеству завоёванных медалей. В десятке лучших команд итальянцы финишировали на зимних Олимпиадах
13 раз. В 2002 году на Олимпиаде в Солт-Лейк-Сити спортсмены Италии завоевали столько же медалей, сколько россияне.
Самой неудачной из последних Олимпиад для итальянцев оказалась Олимпиада в 2010 году, проходившая в Ванкувере
(Канада), где Италия смогла выиграть всего 5 медалей.
Спортсмены США завоевали самое большое количество медалей за всю историю Олимпийских игр – более 2,5 тысяч
медалей, в том числе более 1 тысячи золотых. При этом США лидируют по количеству золотых, серебряных и бронзовых
наград как в сумме по итогам летних и зимних Игр, так и отдельно по итогам летних Игр. По итогам всех зимних игр США
уступают в общем зачёте только Норвегии и Германии. Самыми успешными из зимних игр для США оказались Олимпийские
игры 2010 года в Канаде, где они положили в свою копилку 37 наград. Это на 3 медали больше, чем в 2002 году,
и на 9 больше, чем в 2014 году. На Олимпийских играх в 1994 и 1998 годах команда США выиграла по 13 наград.
На Олимпиаде – 2018 в Пхёнчхане американцы завоевали на 10 медалей больше, чем в 1998 году, и на 2 медали меньше,
чем в 2006 году в Турине.
На основании прочитанного определите страну, достижения
которой соответствуют третьему ряду данных на диаграмме.

12.

Задание № 8
XI Областной Чемпионат командных игр-конкурсов
по математичеcкой грамотности. Старшая лига.
Воспользуйтесь текстом «Пункты на карте города»,
расположенным
справа.
Выберите
все
верные
утверждения, о пунктах на карте города в соответствии
с условием задачи.
Задача. На карте города N расположены пункты и заданы
их координаты:
Пункты на карте города
В городе N дорожные магистрали образуют
квадратную сетку. Магистрали, параллельные
оси абсцисс, в городе называют аллеями,
а магистрали, параллельные оси ординат, –
просеками. Между дорожными магистралями
расположены кварталы.
На фрагменте карты города N, данном ниже,
в начале координат расположен Автопарк (А).
Какие из утверждений верны? В ответ запишите
номера всех верных утверждений.
1) Вокзал и театр расположены на одной аллее;
2) Ранок расположен ближе к автопарку, чем театр;
3) Киноцентр и Стадион расположены на одной просеке;
4) Ближе всех к автопарку расположена Обсерватория;
5) Чтобы от рынка доехать до стадиона, необходимо
пересечь аллею, на которой расположен автопарк.
Фрагмент карты города N

13.

Задание № 9
Воспользуйтесь текстом «Рекламная
статистика», расположенным справа.
Запишите ответы на требования задачи
в виде чисел.
Задача. На рисунке представлена в виде
воронки рекламная статистика пледа.
Стоимость
рекламы
составила
1050 рублей. С помощью воронки
на Рисунке 1 вычислите показатель
кликабельности и стоимость клика.
Рисунок 1
XI Областной Чемпионат командных игр-конкурсов
по математичеcкой грамотности. Старшая лига.
Рекламная статистика
Многие продавцы размещают в Интернете рекламу своих услуг
и товаров в виде баннера (графического изображения
с информацией). По завершении показов рекламы формируется
статистика по размещению. Статистические данные собираются
автоматизированной системой и учитывают результаты обработки
показов и кликов пользователей.
В статистике, в том числе, представлены следующие данные:
Частота показов – среднее количество показов баннера на одного
пользователя за определённый период. Стоимость клика – частное
стоимости рекламы и числа кликов по баннеру:
стоимость рекламы
Стоимость клика =
количество кликов
Показатель кликабельности – процентное отношение числа кликов
по баннеру к числу показов:
количество кликов
Показатель кликабельности =
∙ 100%
количество показов
Внимание! Показатель кликабельности обычно округляют
до десятых долей.
Продолжение на следующем слайде

14.

15.

XI Областной Чемпионат командных игр-конкурсов
по математической грамотности. Старшая лига.
Благодарим за участие!
Желаем удачи
в следующем туре!

English Русский Rules