Презентация1

1.

2. Минимальное остовное дерево

• 1. Алгоритм Краскала

3. 1. Выпишем ребра в порядке возрастания

• (2, 6)= 1
• (3, 6)= 1
• (1, 2)= 2
• (5, 7)= 2
• (6, 7)= 3
• (7, 9)= 3
• (2, 3)= 4
• (2, 4)= 4
• (7, 8)= 4
• (3, 5)= 5
• (5, 9)= 5
• (8, 9)= 7
• (4, 6)= 7

4. Просматриваем по очереди ребра графа

• Ребро (2, 6)= 1 добавляем
остов
• Ребро (3, 6)= 1 добавляем
остов
• Ребро (1, 2)= 2 добавляем
остов
• Ребро (5, 7)= 2 добавляем
остов
• Ребро (6, 7)= 3 добавляем
остов
• Ребро (7, 9)= 3 добавляем
остов
• Ребро (2, 3)= 4 добавляем
остов
• Ребро (2, 4)= 4 добавляем
остов
• Ребро (7, 8)= 4 добавляем
остов
• Ребро (3, 5)= 5 добавляем
остов
• Ребро (5, 9)= 5 добавляем
остов
• Ребро (8, 9)= 7 добавляем
остов
• Ребро (4, 6)= 7 добавляем
остов

5.

• Добавлено 13 ребер при 9 вершинах.
• Алгоритм завершен.
• Его вес равен
1+1+2+2+3+3+4+4+4+5+5+7+7=48

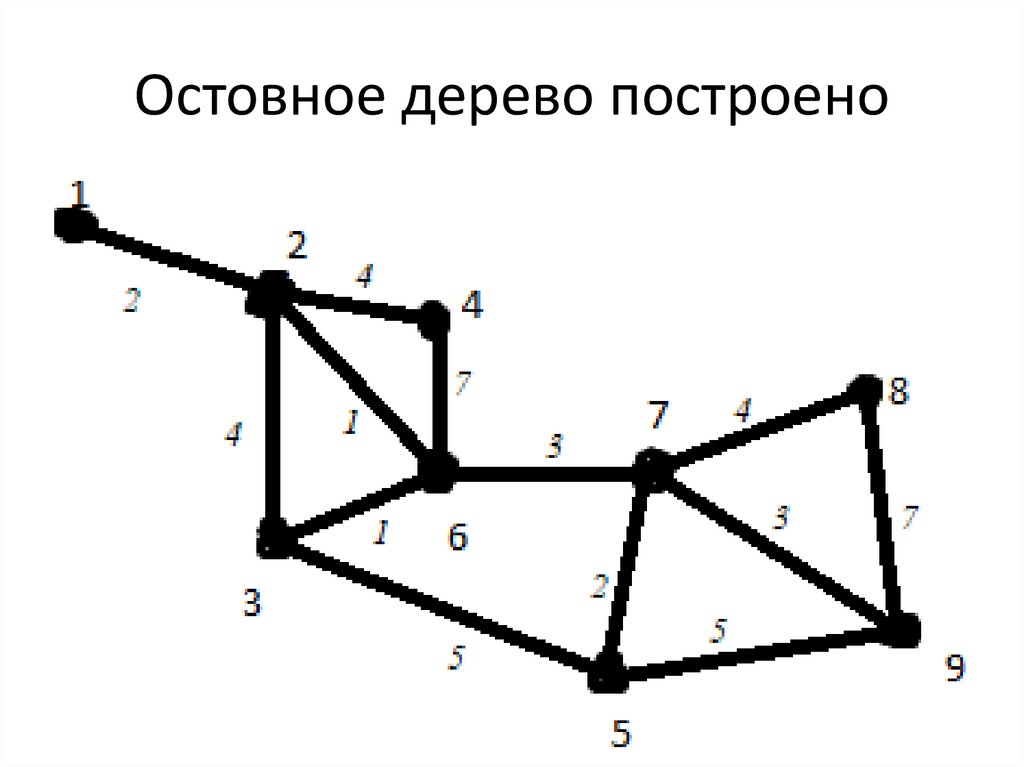
6. Остовное дерево построено

7. Минимальное остовное дерево

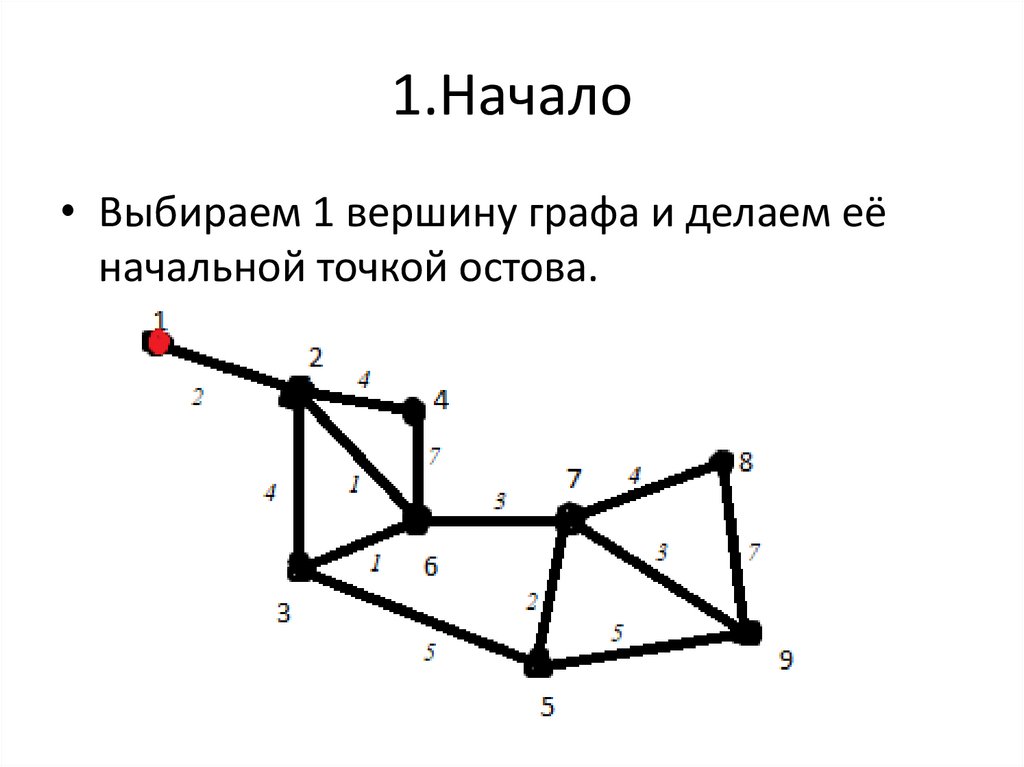
• 2. Алгоритм Прима

8. 1.Начало

• Выбираем 1 вершину графа и делаем её
начальной точкой остова.

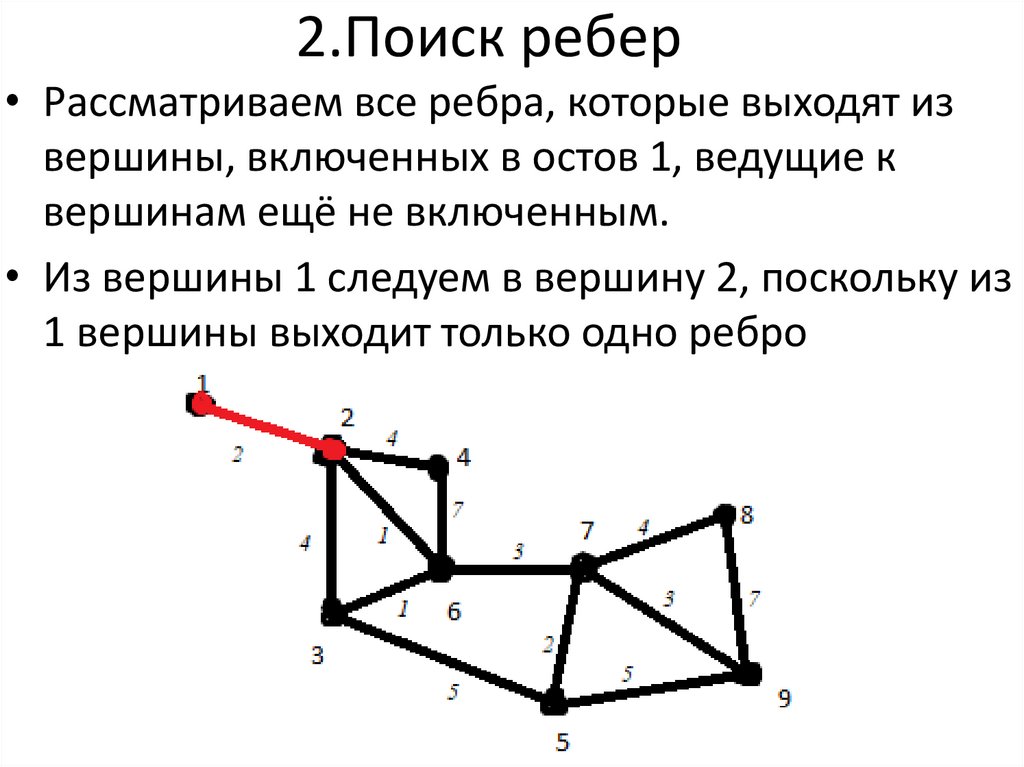
9. 2.Поиск ребер

• Рассматриваем все ребра, которые выходят из
вершины, включенных в остов 1, ведущие к
вершинам ещё не включенным.
• Из вершины 1 следуем в вершину 2, поскольку из
1 вершины выходит только одно ребро

10. 3. Выбор ребра

• Из вершины 2, которая является остовом,
выходят три ребра. Выбираем ребро с
наименьшим весом из имеющихся.
• Ребро (2, 6) = 1 имеет наименьший вес.

11. 4. Повторение шагов 2 и 3

• Все последующие шаги будут описаны словестно
• Из вершины 6 выбираем ребро (3, 6) = 1
• Из вершины 6 выбираем ребро (6, 7) = 3
• Из вершины 7 выбираем ребро (5, 7) = 2
• Из вершины 7 выбираем ребро (9, 7) = 3
• Из вершины 2 выбираем ребро (2, 3) = 4
• Из вершины 2 выбираем ребро (2, 4) = 4
• Из вершины 7 выбираем ребро (7, 8) = 4
• Из вершины 3 выбираем ребро (3, 5) = 5
• Из вершины 5 выбираем ребро (5, 9) = 5
• Из вершины 4 выбираем ребро (4, 6) = 7
• Из вершины 8 выбираем ребро (8, 9) = 7

12.

• Добавлено 13 ребер при 9 вершинах.
• Алгоритм завершен.
• Его вес равен
1+1+2+2+3+3+4+4+4+5+5+7+7=48

13. Вывод

14. Кратчайший маршрут

• 1. Алгоритм Дейкстры
• С помощью данного алгоритма найдем
кратчайшие пути от вершины 1 до всех
остальных

15. Начальные метки вершин

• 1 – (0;-)
• 2 – (∞;-)
• 3 – (∞;-)
• 4 – (∞;-)
• 5 – (∞;-)
• 6 – (∞;-)
• 7 – (∞;-)
• 8 – (∞;-)
• 9 – (∞;-)
• 1 итерация
• Вершина 2 0+2=2 –
обновляем метку ∞

16.

• 1 – (0;-)
• 2 – (2;1)
• 3 – (∞;-)
• 4 – (∞;-)
• 5 – (∞;-)
• 6 – (∞;-)
• 7 – (∞;-)
• 8 – (∞;-)
• 9 – (∞;-)
• Минимальную метку делаем
постоянной (вершина 2)
• 2 итерация
• Вершина 4 2+4=5 – обновляем
метку ∞
• Вершина 6 2+1=3 – обновляем
метку ∞
• Вершина 3 2+4=5 – обновляем
метку ∞

17.

• 1 – (0;-)
• 2 – (2;1)
• 3 – (5;2)
• 4 – (5;2)
• 5 – (∞;-)
• 6 – (3;2)
• 7 – (∞;-)
• 8 – (∞;-)
• 9 – (∞;-)
• Минимальную метку делаем
постоянной (вершина 6)
• 3 итерация
• Вершина 3 3+1=4 – обновляем
метку 5
• Вершина 4 3+7=10 – не обновляем
метку
• Вершина 7 3+3=6 – обновляем
метку ∞

18.

• 1 – (0;-)
• 2 – (2;1)
• 3 – (4;6)
• 4 – (5;2)
• 5 – (∞;-)
• 6 – (3;2)
• 7 – (6;6)
• 8 – (∞;-)
• 9 – (∞;-)
• Минимальную метку делаем
постоянной (вершина 3)
• 4 итерация
• Вершина 2 4+4=8 – не обновляем
метку
• Вершина 5 4+5=9 – обновляем
метку ∞

19.

• 1 – (0;-)
• 2 – (2;1)
• 3 – (4;6)
• 4 – (5;2)
• 5 – (∞;-)
• 6 – (3;2)
• 7 – (6;6)
• 8 – (∞;-)
• 9 – (∞;-)
• Минимальную метку делаем
постоянной (вершина 4)
• 5 итерация
• Вершина 2 5+4=9 – не обновляем
метку
• Вершина 6 5+7=12 – не
обновляем метку

20.

• 1 – (0;-)
• 2 – (2;1)
• 3 – (4;6)
• 4 – (5;2)
• 5 – (∞;-)
• 6 – (3;2)
• 7 – (6;6)
• 8 – (∞;-)
• 9 – (∞;-)
• Минимальную метку делаем
постоянной (вершина 7)
• 6 итерация
• Вершина 6 6+3=9 – не обновляем
метку
• Вершина 5 6+2=8 – обновляем метку
∞
• Вершина 9 6+3=9 – обновляем метку
∞
• Вершина 8 6+4=10 – обновляем метку
∞

21.

• 1 – (0;-)
• 2 – (2;1)
• 3 – (4;6)
• 4 – (5;2)
• 5 – (8;7)
• 6 – (3;2)
• 7 – (6;6)
• 8 – (10;7)
• 9 – (9;7)
• Минимальную метку делаем
постоянной (вершина 5)
• 7 итерация
• Вершина 3 8+5=13 – не обновляем
метку
• Вершина 7 8+2=10 – не обновляем
метку
• Вершина 9 8+5=13 – не обновляем
метку

22.

• 1 – (0;-) • Минимальную метку делаем постоянной
(вершина 9)
• 2 – (2;1)
• 3 – (4;6) • 8 итерация
• 4 – (5;2) • Вершина 5 9+5=14 – не обновляем метку
• 5 – (8;7) • Вершина 8 9+8=17 – не обновляем метку
• 6 – (3;2) • Минимальную метку делаем постоянной
(вершина 8)
• 7 – (6;6)
• 8 – (10;7) • Алгоритм завершен.
• 9 – (9;7)

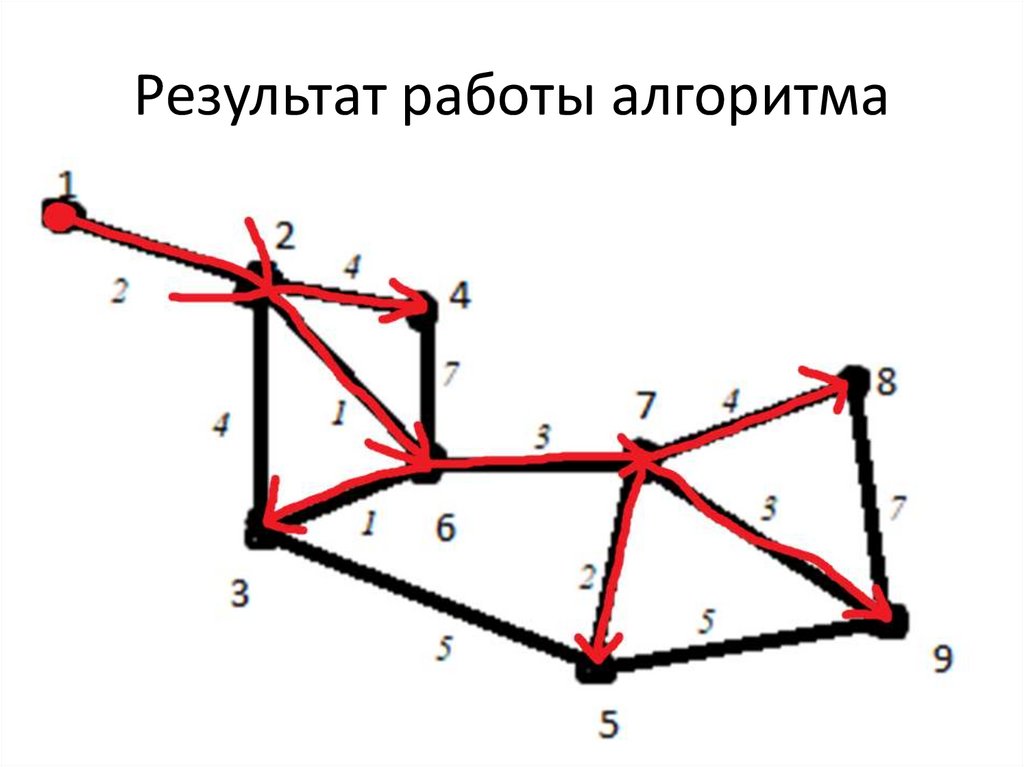
23. Результат работы алгоритма

24.

• До вершины 2 (1-2)
• До вершины 3 (1-2-6-3)
• До вершины 4 (1-2-4)
• До вершины 5 (1-2-6-7-5)
• До вершины 6 (1-2-6)
• До вершины 7 (1-2-6-7)
• До вершины 8 (1-2-6-7-8)
• До вершины 9 (1-2-6-7-9)
• Протяженность 2
• Протяженность 4
• Протяженность 5
• Протяженность 8
• Протяженность 3
• Протяженность 6
• Протяженность 10
• Протяженность 9

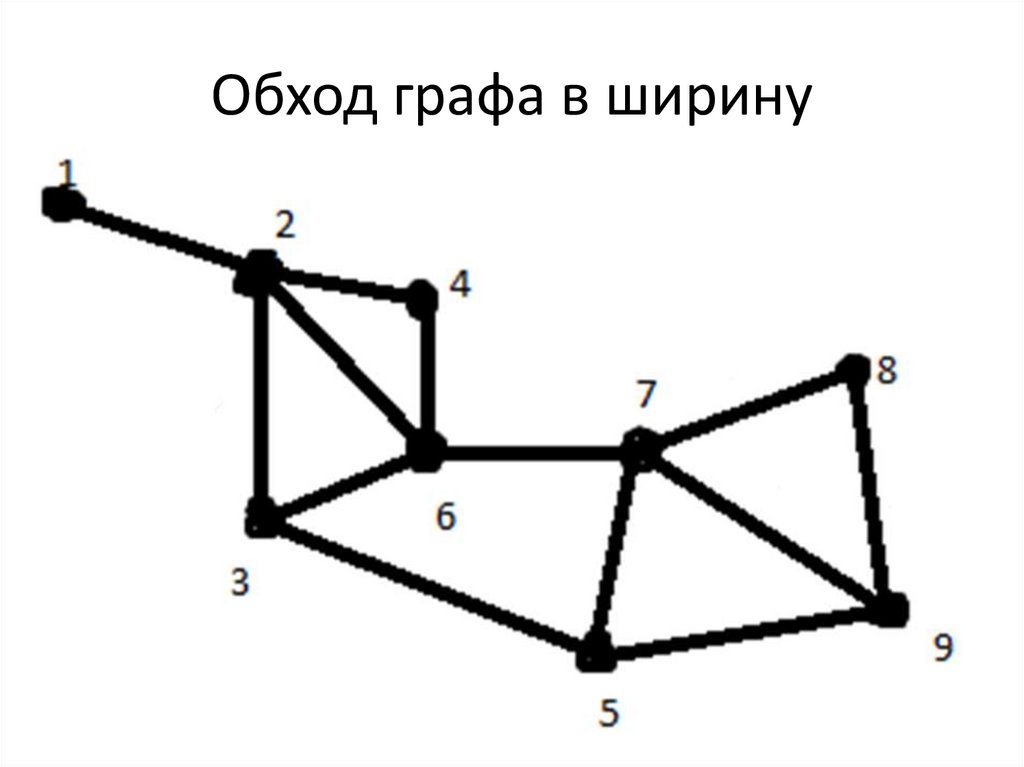
25. Обход графа в ширину

26. Начинаем с вершины 1

• 1) С вершиной 1 смешна только вершина 2. Добавляем её в
очередь. Q = {2}. Извлекаем из очереди вершину 2.
• 2) С вершиной 2 смешны вершины 3,4,6. Добавляем их в
очередь. Q = {3,4,6}. Извлекаем из очереди вершину 3.
• 3) С вершиной 3 смешна только вершина 5. Добавляем её в
очередь. Q = {4,6,5}. Извлекаем из очереди вершину 4.
• 4) У вершины 4 нет смешных не посещенных вершин. Q =
{6,5}. Извлекаем из очереди вершину 6.
• 5) С вершиной 6 смешна только вершина 7. Добавляем её в
очередь. Q = {5,7}. Извлекаем из очереди вершину 5.
• 6) С вершиной 5 смешна только вершина 9. Добавляем её в
очередь. Q = {7,9}. Извлекаем из очереди вершину 7.
• 7) С вершиной 7 смешна только вершина 8. Добавляем её в
очередь. Q = {9,8}. Извлекаем из очереди вершину 9.
• 8) У вершины 9 нет смешных не посещенных вершин. Q = {8}.
Извлекаем из очереди вершину 8.
• 9) У вершины 8 нет смешных не посещенных вершин. Q = Ø
• Очередь пуста. Алгоритм завершен.

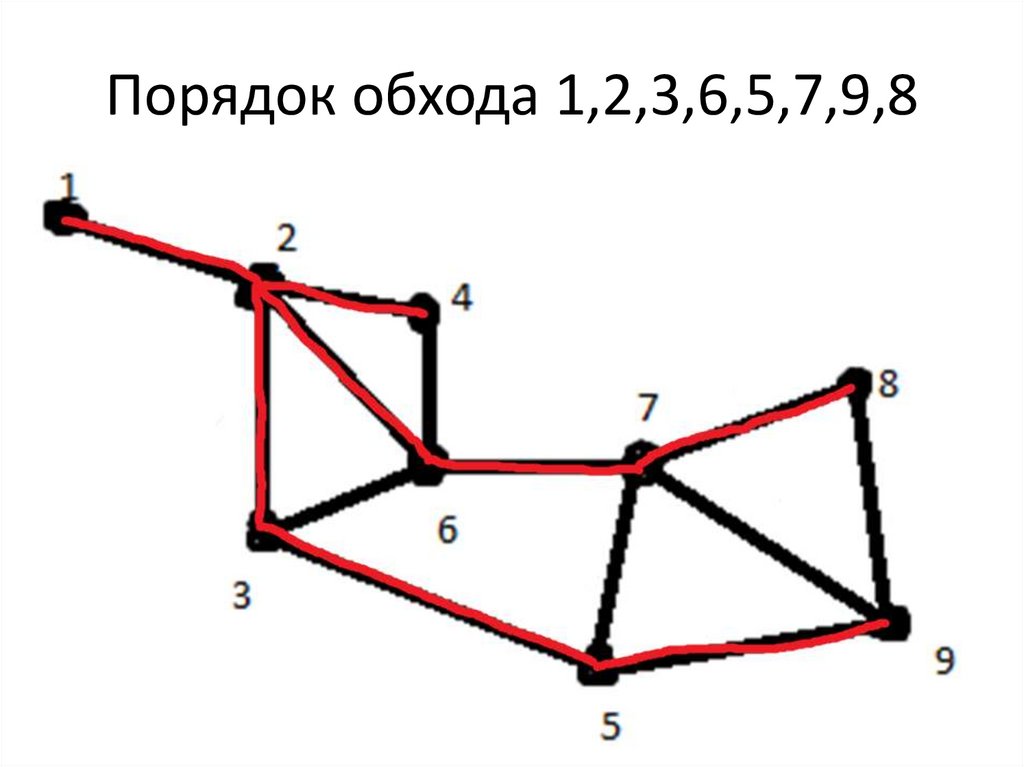
27. Порядок обхода 1,2,3,6,5,7,9,8

28. Обход графа в глубину

• Начинаем с вершины 1

29.

1) Из вершины 1 переходим в вершину 2.
2) Из вершины 2 переходим в вершину 6.
3) Из вершины 6 переходим в вершину 3.
4) Из вершины 3 переходим в вершину 5.
5) Из вершины 5 переходим в вершину 7.
6) Из вершины 7 переходим в вершину 9.
7) Из вершины 9 переходим в вершину 8.
8) У вершины 8 нет не посещенных вершин, возвращаемся в 9
вершину.
9) У вершины 9 нет не посещенных вершин, возвращаемся в 7
вершину.
10) У вершины 7 нет не посещенных вершин, возвращаемся в 5
вершину.
11) У вершины 5 нет не посещенных вершин, возвращаемся в 3
вершину.
12) У вершины 3 нет не посещенных вершин, возвращаемся в 6
вершину.
13) Из вершины 6 переходим в вершину 4.
Алгоритм завершен

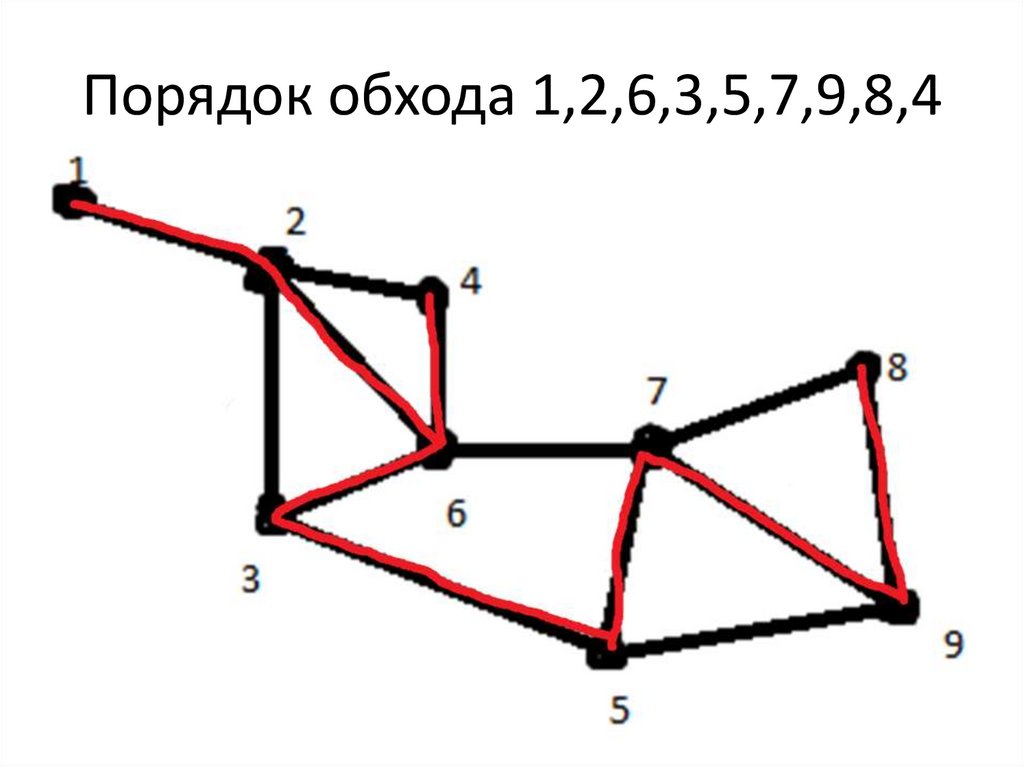
30. Порядок обхода 1,2,6,3,5,7,9,8,4

31. Сравнительный анализ.

• Для поиска в глубину в предложенном
случае потребовалось на 4 хода больше
итераций, чем для поиска в ширину.
Рациональнее использовать обход в
ширину в предложенном случае.