ML.2025.Л 7 ЛОГИКА Логика высказываний

1. Математическая логика и теория алгоритмов

Шошмина Ирина Владимировна
Карпов Юрий Глебович

2. Структура курса

17 лекций
Двоичные функции –
Математическая логика –
Лекция 5. Логика - наука о законах мышления
Лекция 6. Логический вывод в логике высказываний
Лекция 7. Логика предикатов (логика первого порядка)
Лекция 8. Логический вывод в логике предикатов и язык Пролог
Лекция 9. Индуктивный метод Флойда-Хоара верификации программ
Конечные автоматы – преобразователи –
Темпоральные логики и верификация –
Теория алгоритмов –
Ю.Г.Карпов
4л
5л
3л
2л
3л
Математическая логика и теория алгоритмов
2

3. Лекция 5

Логика - наука о законах мышления
Как надо рассуждать, чтобы получить
правильные выводы?

4. Логика – что это?

Логикой ученые занимались много веков. Уже древние греки (4-й век ВС)
знали операции над высказываниями, т.е. над утверждениями, каждое из
которых могло иметь значения “истина” или “ложь”.
Логика исходит из идеи о том, что, записав все исходные допущения на
языке знаков, похожих на математические, можно заменять рассуждение
вычислением
Логика изучает формальные структурные свойства мышлѐния, способы
представления знаний в формальных языках, методы анализа формул,
которыми формально представляются утверждения. Логика упорядочивает
мышление
Предметом логики являются функции и структура мышления, его
применение в практической деятельности. Логика является наукой о
формах и законах правильного мышления. Правильным является такой
способ мышления, который приводит к выводам, которые соответствуют
действительности в соответствующих обстоятельствах
Иммануил Кант: “Логика является цензурой мысли”
Мы будем рассматривать математическую логику как математическую
модель дедуктивных умозаключений. Основная задача курса - обучение
правильным способам рассуждения
Ю.Г.Карпов
Математическая логика и теория алгоритмов
4

5. Логика

Логика
не исследует мышления,
не исследует пути постижения истины,
не исследует она и то, является ли данное конкретное простое
утверждение истинным либо ложным
Логика позволяет судить об истине, рассматривая форму и структуру
мышления независимо от содержания мышления – конкретных объектов и
их свойств
Такой подход возможен, благодаря объективно существующим
закономерностям и связанной с ними упорядоченности окружающего мира.
Если мышление протекает в соответствии с этими закономерностями, его
естественно назвать правильным
Математическая логика выражает закономерности, которые мы можем
назвать законами правильного мышления – законам причинно-следственной
связи. Если мы строим свои рассуждения в соответствии с этими
закономерностями, то эти рассуждения (в оговоренных обстоятельствах, в
которых работают эти закономерности), будут являться правильными т.е.
давать ответы, объективно соответствующие реальности
Ю.Г.Карпов
Математическая логика и теория алгоритмов
5

6. Логика высказываний

Первый раздел логики – пропозициональная логика (proposition logic), логика
высказываний
Высказывание – это утверждение, (мысль, выраженная повествовательным
предложением) которое может быть истинным либо ложным. В классической логике
рассматривается только два истинностных значения высказывания (Истина либо Ложь)
“Идет дождь”, “Дорога сухая”, “Если идет дождь, то дорога не сухая”
Высказывания могут быть либо элементарными (атомарными) утверждениями, либо
сложными, составными. Атомарность означает, что мы не интересуемся СТРУКТУРОЙ
высказывания, они для нас имеют только одну характеристику – их значение, которое
может быть либо Истина, либо Ложь
“Москва – столица России”, “2 + 2 = 4”, “Я люблю Машу” , “Дорога сухая”
Сложные (составные) высказывания составляются из атомарных с помощью связок И,
ИЛИ, НЕ и других. Их характеристика Истина, либо Ложь зависит от их структуры и
истинностных значений составляющих их атомарных высказываний
Если “свет включен”, а “лампочка не горит”, то или “нет электричества”,
или “перегорели пробки”, или “неисправна лампочка”
Логика высказываний отражает то, как истинность сложных
высказываний зависит от истинности составляющих его атомарных
высказываний
Ю.Г.Карпов
Математическая логика и теория алгоритмов
6

7. Логика высказываний рассматривает формулы

“Если сейчас выпадает решка, то я не люблю Машу, а люблю Дашу”
Элементарное высказывание мы можем представить логической
переменной, которая может принимать два значения – Ложь либо Истина
“Сейчас выпадает решка” - Р - или выпадет, или не выпадет
“Я люблю Машу”
- М - или люблю, или не люблю Машу
“Я люблю Дашу”
- Д - или люблю, или не люблю Дашу
Сложные высказывания можно представить формулами над логическими
переменными, принимающими значения Ложь и Истина
“Если сейчас выпадает решка, то я не люблю Машу, а люблю Дашу”
“Если
Р , то НЕ
М,
а
Р М
Ю.Г.Карпов
Д
”
Д
Математическая логика и теория алгоритмов
7

8. Логика высказываний манипулирует формулами (ППФ)

Когда формула является ППФ (правильно построенной формулой)?
атомарные высказывания являются ППФ
если f1 и f2 являются ППФ, то f1 и f1 f2 – тоже являются ППФ
Семантика (смысл) каждой ППФ задается таблицами истинности:
f
f
f1 f2
f1 f2
Л
И
ЛЛ
Л
И
Л
ЛИ
И
ИЛ
И
ИИ
И
Синтаксис (структура) - правила построения
формул, определяет, как строить формулы
Строго говоря, знаки операций в двоичных функциях
и в ППФ логики высказываний должны быть разными
(поскольку сами модели и смысл операций разные)
Выводимые связки задаются правилами:
( ( f1) ( f2) ) обозначается f1 f2
( f1) f2 обозначается f1 f2
f f обозначается Истина
Истина обозначается Ложь
...
Дизъюнктивный базис! Могут быть и другие
Ю.Г.Карпов
Математическая логика и теория алгоритмов
8

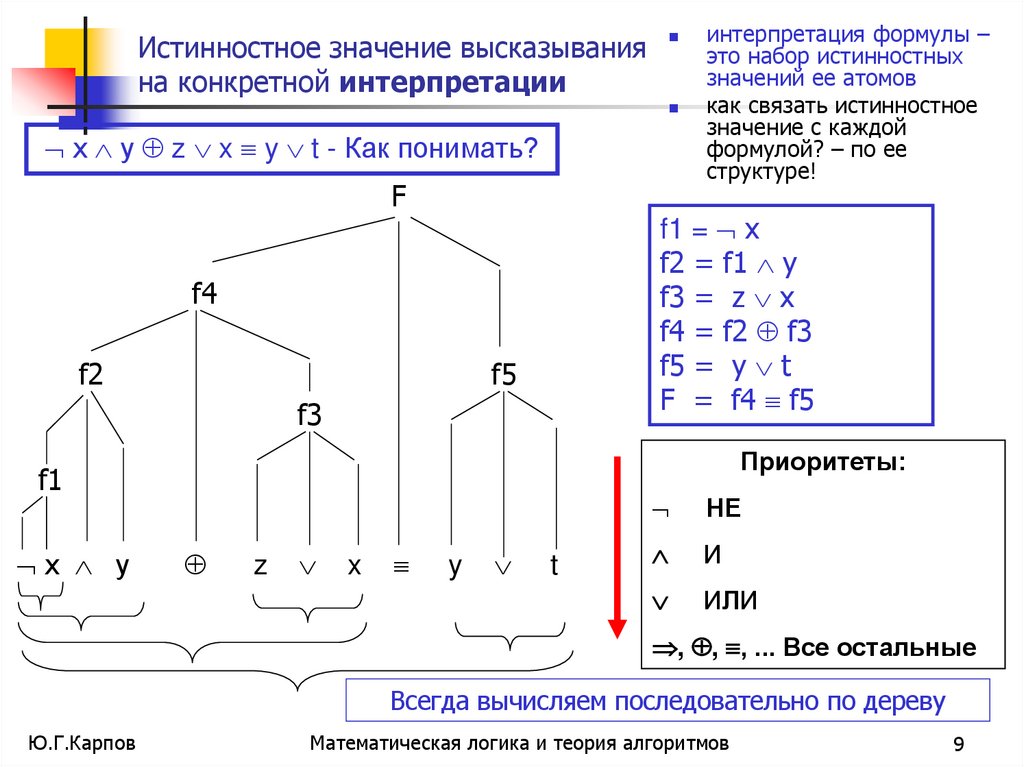
9. Истинностное значение высказывания на конкретной интерпретации

х у z x y t - Как понимать?
F
f1 = х
f2 = f1 y
f3 = z x
f4 = f2 f3
f5 = y t
F = f4 f5
f4
f2
f5
f3
Приоритеты:
f1
х у
интерпретация формулы –
это набор истинностных
значений ее атомов
как связать истинностное
значение с каждой
формулой? – по ее
структуре!
z
x
y
t
НЕ
И
ИЛИ
, , , ... Все остальные
Всегда вычисляем последовательно по дереву
Ю.Г.Карпов
Математическая логика и теория алгоритмов
9

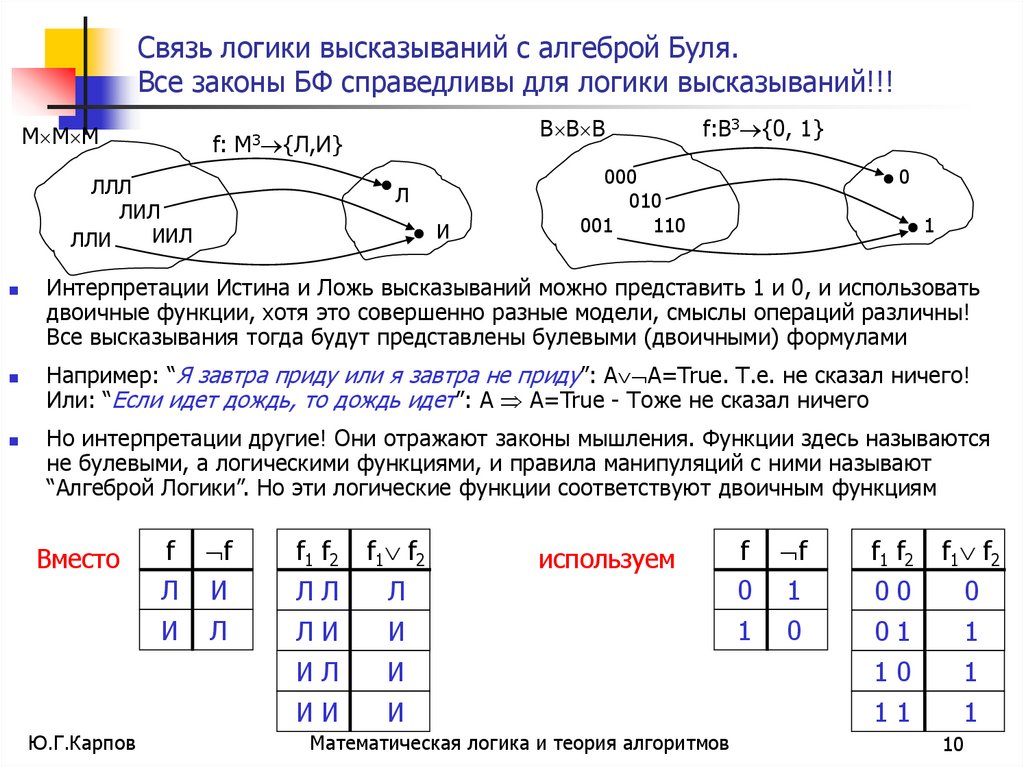
10. Связь логики высказываний с алгеброй Буля. Все законы БФ справедливы для логики высказываний!!!

М М М
ЛЛЛ
ЛИЛ
ИИЛ
ЛЛИ
В В В
f: М3 {Л,И}
Л
И
f:В3 {0, 1}
000
010
001
110
0
1
Интерпретации Истина и Ложь высказываний можно представить 1 и 0, и использовать
двоичные функции, хотя это совершенно разные модели, смыслы операций различны!
Все высказывания тогда будут представлены булевыми (двоичными) формулами
Например: “Я завтра приду или я завтра не приду”: А А=True. Т.е. не сказал ничего!
Или: “Если идет дождь, то дождь идет”: А А=True - Тоже не сказал ничего
Но интерпретации другие! Они отражают законы мышления. Функции здесь называются
не булевыми, а логическими функциями, и правила манипуляций с ними называют
“Алгеброй Логики”. Но эти логические функции соответствуют двоичным функциям
Вместо
Ю.Г.Карпов
f
f
f1 f2
f1 f2
f
f
f1 f2
f1 f2
Л
И
ЛЛ
Л
0
1
00
0
И
Л
ЛИ
И
1
0
01
1
ИЛ
И
10
1
ИИ
И
11
1
используем
Математическая логика и теория алгоритмов
10

11. ППФ логики высказываний и двоичные функции

Соответствуют ли наше понимание истинности и ложности во всех
контекстах единице и нулю двоичных формул??? И наоборот??? ДА!
Любая ППФ логики высказываний является логической функцией над
логическими переменными, принимающими значения {Истина, Ложь}, или
двоичными функциями над двоичными переменными со значениями в {0, 1}
Базисы логических функций – те же, что и у двоичных функций. Поэтому
любую ППФ можно представить формулой, состоящей только из логических
функций базиса
Интерпретацией логической функции называется набор истинностных
значений ее аргументов
Это отражает очень глубокую мысль:
“ЛЮБОЕ РАССУЖДЕНИЕ может быть выражено только с помощью
атомарных утверждений и связок И, ИЛИ, НЕ (и даже еще более
просто, с помощью {И, НЕ}, {ИЛИ, НЕ}, ...)”
Нильс Бор: «Отрицание правильного высказывания – ложное высказывание. Но
отрицанием глубокой истины может быть только другая глубокая истина»
Ю.Г.Карпов
Математическая логика и теория алгоритмов
11

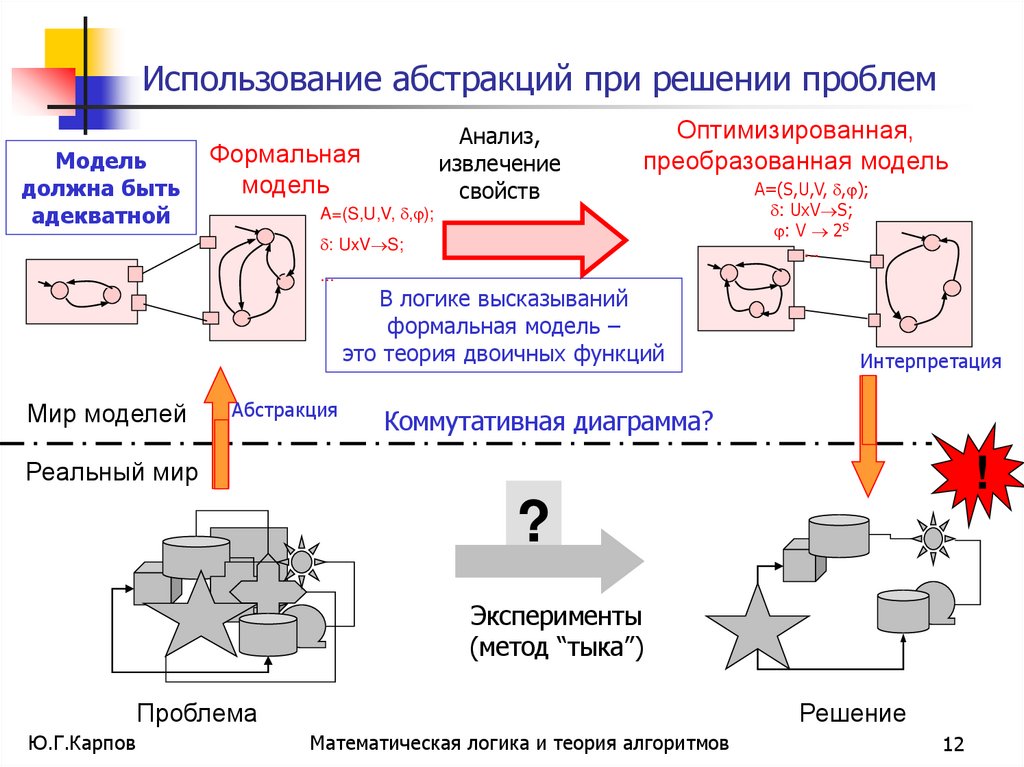
12. Использование абстракций при решении проблем

Модель
должна быть
адекватной
Формальная
модель
A=(S,U,V, , );
Анализ,
извлечение
свойств
Оптимизированная,
преобразованная модель
: UxV S;
...
Мир моделей
Абстракция
В логике высказываний
формальная модель –
это теория двоичных функций
A=(S,U,V, , );
: UxV S;
: V 2S
...
Интерпретация
Коммутативная диаграмма?
!
Реальный мир
?
Эксперименты
(метод “тыка”)
Проблема
Ю.Г.Карпов
Решение
Математическая логика и теория алгоритмов
12

13. Связь логики высказываний с алгеброй Буля (II)

Анализ формул, которые являются моделями сложных высказываний,
выполняется на основе логических функций, которые являются, фактически,
двоичными функциями
Теория двоичных функций и ее результаты делает правила манипулирования
логическими функциями очень простыми (НО изначально двоичные функции
были придуманы именно как логические функции)!
ДЛЯ РЕШЕНИЯ ПРОБЛЕМ с помощью формализма, нужно выполнить два шага
первый шаг: в данном сложном высказывании естественного языка
выделить атомарные высказывания
второй шаг: представить отношения между атомарными высказывании в
сложном высказывании операциями логики (двоичными функциями),
это НЕ всегда однозначно! ОБА ШАГА часто можно сделать по-разному
только формальные преобразования в рамках формальной модели по
формальным правилам дают однозначный ответ
Ю.Г.Карпов
Математическая логика и теория алгоритмов
13

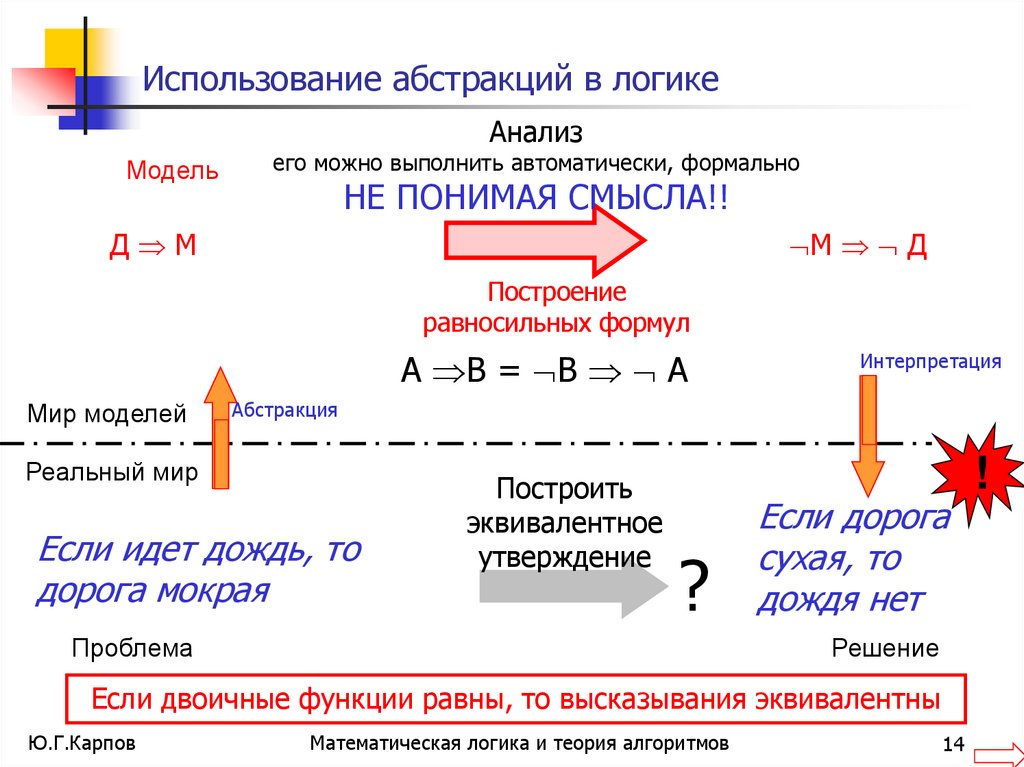
14. Использование абстракций в логике

Анализ
Модель
его можно выполнить автоматически, формально
НЕ ПОНИМАЯ СМЫСЛА!!
Д М
M Д
Построение
равносильных формул
А В = В А
Мир моделей
Интерпретация
Абстракция
Реальный мир
Если идет дождь, то
дорога мокрая
Построить
эквивалентное
утверждение
?
Проблема
Если дорога
сухая, то
дождя нет
Решение
Если двоичные функции равны, то высказывания эквивалентны
Ю.Г.Карпов
Математическая логика и теория алгоритмов
14
!

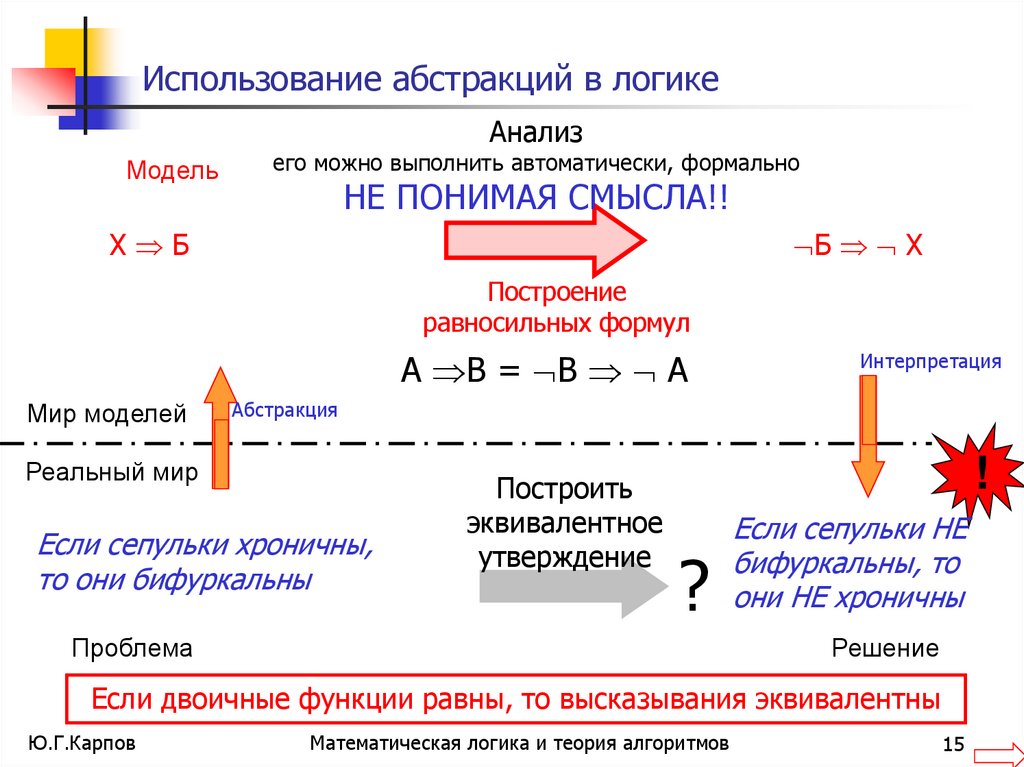
15. Использование абстракций в логике

Анализ
Модель
его можно выполнить автоматически, формально
НЕ ПОНИМАЯ СМЫСЛА!!
Х Б
Б Х
Построение
равносильных формул
А В = В А
Мир моделей
Интерпретация
Абстракция
Реальный мир
Если сепульки хроничны,
то они бифуркальны
Построить
эквивалентное
утверждение
!
?
Проблема
Если сепульки НЕ
бифуркальны, то
они НЕ хроничны
Решение
Если двоичные функции равны, то высказывания эквивалентны
Ю.Г.Карпов
Математическая логика и теория алгоритмов
15

16. Связки естественного языка и логические операции

Абстрагирование: Как от фразы естественного языка перейти к формуле?
Фразы
Обозначение операции
не А; неверно, что A; А неверно;
A, ~A, !А
А или В; или А, или В, или то и другое вместе
А В, А or В
и А, и В; как А, так и В; не только А, но и В
А В, A&B, AB
либо А, либо В, но не то и другое вместе;
exlusive OR; XOR
А В
если А, то В; А влечет В; В тогда, когда А;
(А-посылка, В-заключение)
A B, A B, A B
А если и только если В; как А, так и В;
А эквивалентно В
А В, А В
A B (правило if-then)
А – посылка, антецедент,
Ю.Г.Карпов
В – заключение, консеквент
Математическая логика и теория алгоритмов
16

17. Сложные высказывания

Сложные высказывания состоят из ряда простых. Различают
конъюнктивные, дизинъюнктивные, импликационные, эквивалентные и
отрицательные высказывания
Дизъюнктивные высказывания образуются с помощью разделительных
(дизъюнктивных) логических связок аналогичных союзу «или» в руском
языке. Подобно простым разделительным суждениям бывают нестрогими
(нестрогая дизинъюнкция), члены которой допускают совместное
сосуществование (толи…, толи…), записывающимися a b; и строгими
(строгая дизинъюнкция) члены которой исключают друг друга (либо одно,
либо другое, но не оба вместе), записывающимися a b
Импликационные суждения образуются с помощью импликации,
эквивалентной союзу «если …, то» и записываются a b
Конъюнктивные суждения образуются с помощью логических связок
сочетания (конъюнкции), запятой или союзов «и», «а», «но», «да»,
«хотя», «который», «зато» и другим. записываются a b
Эквивалентные суждения указывают на тождественность частей
суждения друг другу (проводят между ними знак равенства).
Записываются a b
Отрицательные суждения строятся с помощью связок «не», «неверно,
что …» и т.д., и записываются а
Ю.Г.Карпов
Математическая логика и теория алгоритмов
17

18. Роль абстракции и формальных моделей при анализе и синтезе (разработке) сложных систем

Логика как теоретическая наука изучает МОДЕЛИ правильных
рассуждений
С помощью абстрагирования можно перевести решение проблем анализа
рассуждений из мира высказываний естественного языка, полного
неопределенностей и двусмысленностей, в мир моделей, мир математики,
где отношения между объектами или высказываниями определяются
совершенно строго и формально. Эти формы и изучает математическая
логика
Абстракция – процесс упрощения, отбрасывания деталей при описании
систем с тем, чтобы были выявлены главные, основные характеристики
системы
Абстракция является ключом к рациональному мышлению на основе
законов логики
Ю.Г.Карпов
Математическая логика и теория алгоритмов
18

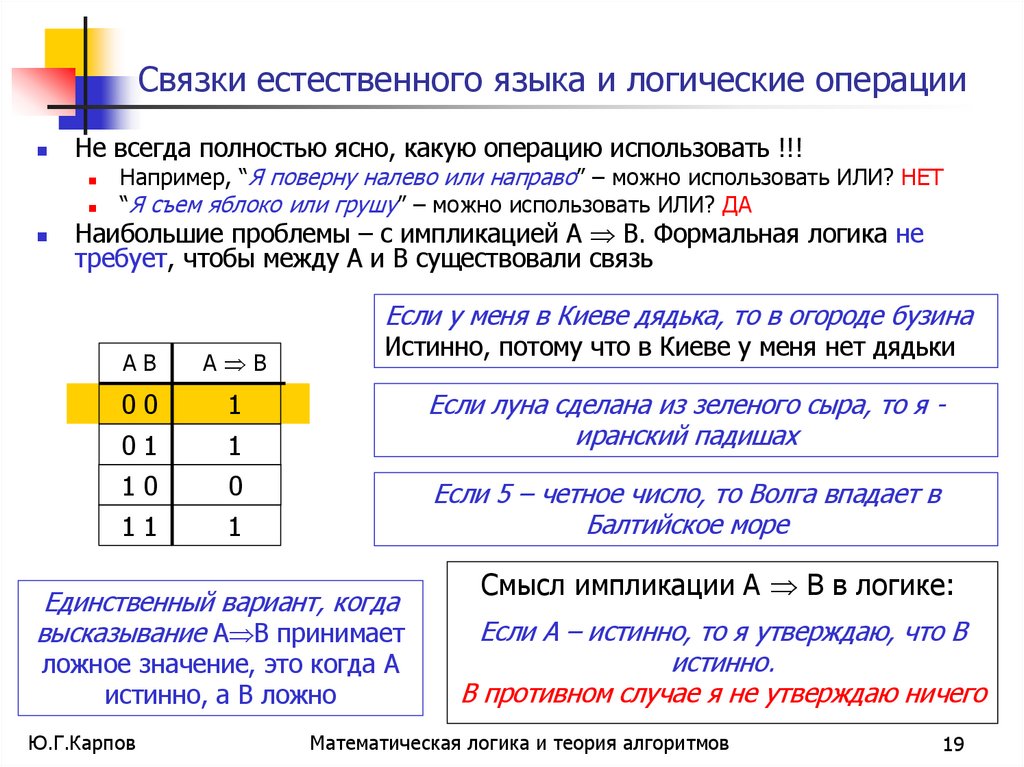
19. Связки естественного языка и логические операции

Не всегда полностью ясно, какую операцию использовать !!!
Например, “Я поверну налево или направо” – можно использовать ИЛИ? НЕТ
“Я съем яблоко или грушу” – можно использовать ИЛИ? ДА
Наибольшие проблемы – с импликацией А В. Формальная логика не
требует, чтобы между А и В существовали связь
Если у меня в Киеве дядька, то в огороде бузина
АВ
А В
00
1
01
1
10
0
11
1
Истинно, потому что в Киеве у меня нет дядьки
Если луна сделана из зеленого сыра, то я иранский падишах
Если 5 – четное число, то Волга впадает в
Балтийское море
Единственный вариант, когда
высказывание А В принимает
ложное значение, это когда А
истинно, а В ложно
Ю.Г.Карпов
Смысл импликации А В в логике:
Если А – истинно, то я утверждаю, что В
истинно.
В противном случае я не утверждаю ничего
Математическая логика и теория алгоритмов
19

20. Импликация в математической логике

Употребление слов “если…, то…” в математической логике отличается от
употребления их в обыденной речи, где мы обычно считаем, что если
высказывание х ложно, то высказывание “если х, то y” не имеет смысла.
При использовании предложения вида “если х, то y” в обыденной речи, мы
всегда подразумеваем, что предложение y причинно зависит (следует,
вытекает) из предложения х
Использование операции импликации (и слов слов “если…, то…”) в
математической логике не требует этого, поскольку в формальной логике
смысл высказываний не рассматривается, мы от содержания высказываний
абстрагируемся, оперируя только формой
Ю.Г.Карпов
Математическая логика и теория алгоритмов
20

21. Понимание импликации. Wason card puzzle

Peter Wason, английский психолог, сформулировал интересную
проблему, которая интенсивно изучается в психологии
Проблема: Даны четыре карты, на одной стороне
РQ
которых число, на другой – буква
00
А
M
4
7
1
01
1
10
0
11
1
Подняв наименьшее число карт, проверить утверждение:
“Если на одной стороне гласная, то на другой – четное число”
P Q
Только 4% людей дают правильный ответ
Вариант этой проблемы: Проверить, справедливо ли правило
“Если на одной стороне М, то на другой – 7 ”
Большинство дает ответ М и 7. Правильно?
Ю.Г.Карпов
Математическая логика и теория алгоритмов
21

22. Задачи, которые мы рассмотрим в рамках логики высказываний

Анализ и преобразование сложных высказываний
является ли данное высказывание тавтологией – т.е. всегда истинным
(либо, что то же – является ли высказывание невыполнимым)?
Доказательство теорем
эквивалентны ли два высказывания?
какова структура формулируемой теоремы?
как доказывать теорему – как свести доказательство сложной теоремы
к доказательству более простых утверждений (теорем)?
Логическое следствие
как определить, что одно высказывание является логическим
следствием заданных высказываний?
как строить умозаключение – вывод некоторого заключения (нового
знания) из установленных фактов – базы знаний?
Фактически, логика учит методам правильного рассуждения
Ю.Г.Карпов
Математическая логика и теория алгоритмов
22

23. Эквивалентность высказываний

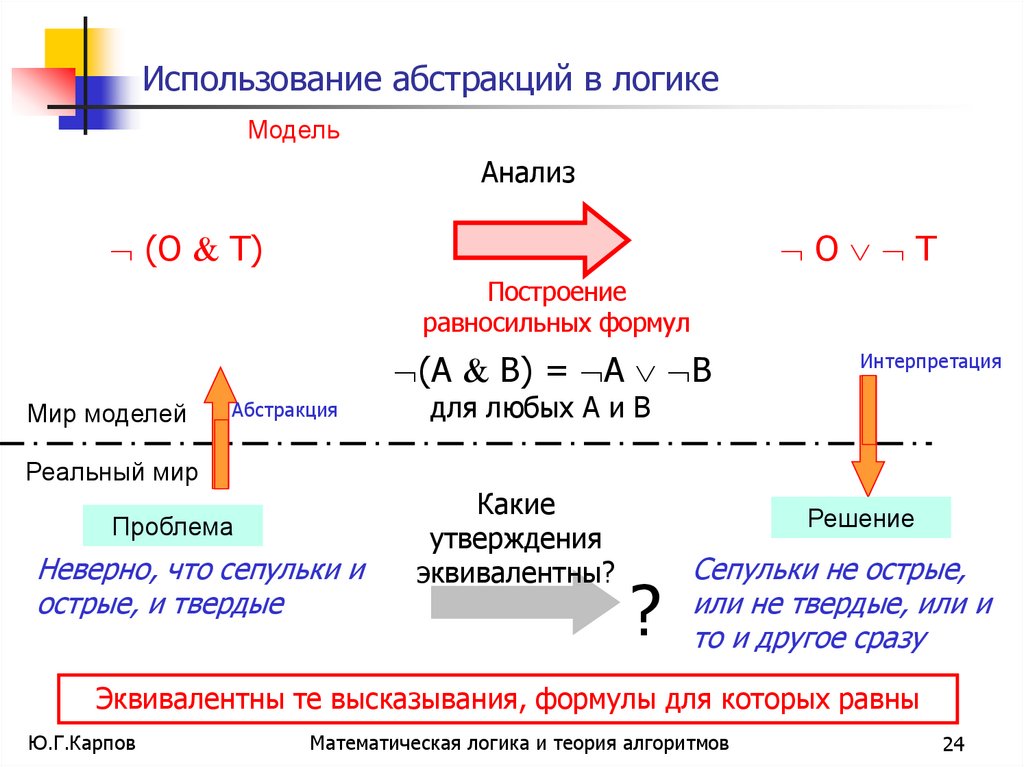
24. Использование абстракций в логике

Модель
Анализ
(О Т)
О Т
Построение
равносильных формул
(А В) = А В
Мир моделей
Абстракция
Реальный мир
Проблема
Неверно, что сепульки и
острые, и твердые
Интерпретация
для любых А и В
Какие
утверждения
эквивалентны?
Решение
?
Сепульки не острые,
или не твердые, или и
то и другое сразу
Эквивалентны те высказывания, формулы для которых равны
Ю.Г.Карпов
Математическая логика и теория алгоритмов
24

25. Свойства двоичных функций и эквивалентные высказываний в логике

Законы де Моргана (А В) = А В
Неверно, что обвиняемый является одновременно и исполнителем и
организатором преступления. Это значит, что или обвиняемый не
является исполнителем преступления, или же он не является
организатором этого преступления, или же и то, и другое вместе
А (В С) = А В А С
Петров трус и он или любит мясо,, или же он любит рыбу. Это значит,
что или Петров трус и любит мясо, или Петров трус и любит рыбу, или
же и то, и другое вместе
Ю.Г.Карпов
Математическая логика и теория алгоритмов
25

26. Эквивалентность высказываний

Построение эквивалентных высказываний с помощью контрапозиции
X Y =
АВ
Y X
А В А В
( Y X контрапозиция X Y)
В А
00
1
1
1
01
1
1
1
10
1
1
1
11
0
0
0
А В
А В
В А
А – он – порядочный человек
В – он вор
А В = А В =
В А
Порядочный человек не может быть вором
Или он не порядочный человек, или он не вор
Если он вор, то он не порядочный человек
Вор не является порядочным человеком
Если функции равны, то соответствующие высказывания эквивалентны
Ю.Г.Карпов
Математическая логика и теория алгоритмов
26

27. Тезис Черча-Тьюринга

Тезис Черча-Тьюринга
Формулировка утверждения (высказывания)
Если существует какой-либо алгоритм решения проблемы, то его
можно реализовать на машине Тьюринга
В виде формулы логики высказываний:
Существует_А Можно_реализовать_А_на_МТ
КОНТРАПОЗИЦИЯ тезиса
В виде формулы логики высказываний:
Можно_реализовать_А_на_МТ Существует_А
Эквивалентная формулировка
Если алгоритм решения некоторой проблемы НЕ может быть
реализован на машине Тьюринга, то НЕ существует алгоритма,
который решает эту проблему
Мы можем построить эквивалентную формулировку, совершенно не понимая,
о чем идет речь, оперируя лишь ФОРМОЙ высказывания
Ю.Г.Карпов
Математическая логика и теория алгоритмов
27

28. Тест на логическое мышление

При условии, что следующее высказывание правильно:
Говорят, что сепульки и острые, и твердые. Оказывается, это вовсе не так
Установить, какое из следующих утверждений эквивалентно ему
а) на самом деле сепульки тупые и мягкие;
b) на самом деле сепульки или тупые, или мягкие, или то и другое сразу;
c) на самом деле сепульки тупые или мягкие, но не то и другое сразу
Решаем задачу, используя модель – логику высказываний
Шаг 1 – выделяем атомарные высказывания
О - сепульки острые ( значит, О – сепульки тупые)
Т – сепульки твердые ( значит, Т – сепульки мягкие)
Шаг 2 – строим абстракцию исходного высказывания – формулу логики
(О Т) – абстрактная модель высказывания “неверно, что сепульки и
острые, и твердые”,
Шаг 3 – преобразуем все формулы в ДНФ: исходное : (О Т)= О Т;
а) О Т; б) О Т; в) О Т
Шаг 4 – сравниваем формулу для исходного и формулы для а), b) и c).
Совпадает b)
Ю.Г.Карпов
Математическая логика и теория алгоритмов
28

29. Анализ сложных высказываний

Если число делится на 6, то оно делится и на 3, и на 2
Д6 Д3 & Д2
Дk – число делится на k
Строим контрапозицию:
(Д3 & Д2) Д6
Если неверно, что число делится и на 3, и на 2, то оно не делится на 6
Используем теорему де Моргана: (А & В) = А В
Д3 Д2 Д6
Если число не делится на 3 , ИЛИ число не делится на 2, то оно не делится на 6
Поскольку формулы равносильны, то все эти три интерпретации
эквивалентны
Ю.Г.Карпов
Математическая логика и теория алгоритмов
29

30. Анализ сложных высказываний. Преобразование к эквивалентным высказываниям

Симпсон будет признан судом виновным тогда и только тогда, когда все 12
присяжных заседателей признают его виновным
выразим формулой:
Симпсон_Виновен П1& П2& …&П12
A B = A B
Равносильная формула: Симпсон_Виновен (П1& П2& …&П12)
Правую часть преобразуем по закону Де Моргана :
Симпсон_Виновен П1 П1 ... П12
Эта формула может быть интерпретирована так:
Симпсон не будет признан судом виновным тогда и только тогда, когда хотя
бы один из 12 присяжных заседателей не признает его виновным
Ю.Г.Карпов
Математическая логика и теория алгоритмов
30

31. Преобразование высказываний. Эквивалентность

“Волков бояться – в лес не ходить” Схема высказывания: В Л
В лес ходить – волков не бояться” Схема высказывания: Л В
Л В – контрапозиция высказывания В Л , следовательно,
высказывания эквивалентны
“Граф взаимных ожиданий процессов будет ациклическим тогда и только
тогда, когда в системе процессов нет дедлока (блокировки) ”
Схема высказывания: Ц Д.
Эквивалентная формула: Ц Д
“Граф взаимных ожиданий процессов будет иметь цикл тогда и только
тогда, когда в системе процессов есть дедлок”
Ю.Г.Карпов
Математическая логика и теория алгоритмов
31

32. Упрощение сложных высказываний

Условие достижения консенсуса в компьютерной сети
П = Б
С = А
О = Н
Ш = Т
Четыре параметра:
тип процессоров: синхронные (С) или асинхронные (А)
порядок сообщений в канале: сохраняется (П), без сохранения (Б)
передача сообщений: широковещательная (Ш), точка-точка (Т)
коммуникации во времени: ограничена (О), нет (Н)}
Результаты исследований: консенсуса можно достигнуть в следующих случаях:
(1) процессоры асинхронные, порядок сообщений сохраняется, передача сообщений
широковещательная и время коммуникации не ограниченно ИЛИ
(2) процессоры асинхронные, порядок сообщений сохраняется, передача сообщений
широковещательная и время коммуникации ограничено ИЛИ
(3) процессоры синхронные, порядок сообщений НЕ сохраняется, передача сообщений
точка-точка и время коммуникации ограничено ИЛИ
.....
(8) ...
Иными словами, логическая функция Kонсенус истинна на 8 наборах значений
(А,П,Ш,Н), (А,П,Ш,О), (С,Б,Т,О), (С,Б,Ш,О), (С,П,Ш,Н), (С,П,Ш,О), (С,П,Т,Н),
(С,П,Т,О), ... где А = С, Б= П и т.д.
Как коротко сформулировать условия достижимости консенсуса в вычислительных
сетях?
J.Turek, D.Sasha. The many Faces of Consensus in Distributed Systems//IEEE Computer, July, 1992
Ю.Г.Карпов
Математическая логика и теория алгоритмов
32

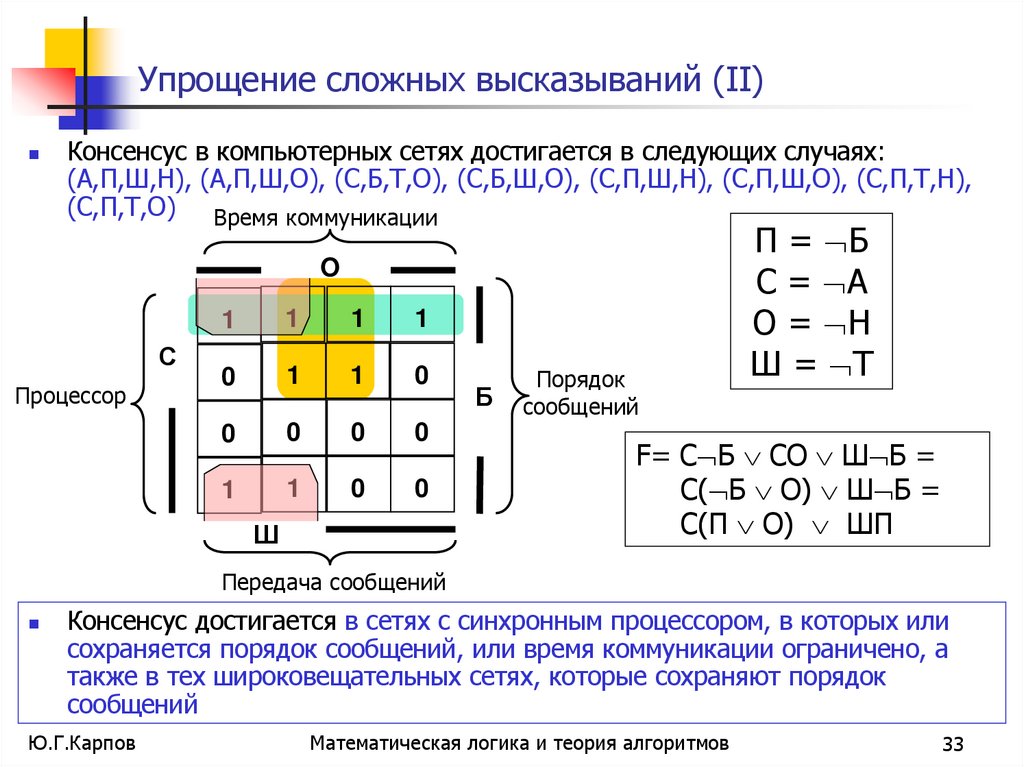
33. Упрощение сложных высказываний (II)

Консенсус в компьютерных сетях достигается в следующих случаях:
(А,П,Ш,Н), (А,П,Ш,О), (С,Б,Т,О), (С,Б,Ш,О), (С,П,Ш,Н), (С,П,Ш,О), (С,П,Т,Н),
(С,П,Т,О) Время коммуникации
O
С
Процессор
1
1
1
1
0
1
1
0
0
0
0
0
1
1
0
0
Ш
Б
Порядок
сообщений
П = Б
С = А
О = Н
Ш = Т
F= С Б СO Ш Б =
С( Б O) Ш Б =
С(П O) ШП
Передача сообщений
Консенсус достигается в сетях с синхронным процессором, в которых или
сохраняется порядок сообщений, или время коммуникации ограничено, а
также в тех широковещательных сетях, которые сохраняют порядок
сообщений
Ю.Г.Карпов
Математическая логика и теория алгоритмов
33

34. Структура доказательства теорем

35. Доказательство теорем. Использование эквивалентностей

Импликация и ее контрапозиция эквивалентны: A B = B A
Доказательство от противного reductio ad absurdum.
AB
Нужно доказать, что если А, то В. Предположим
противное, т.е. что НЕ В. Покажем, что при этом
предположении А будет ложным, т.е. докажем НЕ А.
<доказательство того, что А не выполняется>
Мы пришли к противоречию, доказали, что если
не В, то не А. Следовательно, верно что если А, то B
00
1
1
01
1
1
10
0
0
11
1
1
A B B A
Пример. Доказать:
Если сепульки гомозиготны, то они контрарны
Доказательство. Предположим противное, т.е. что сепульки НЕ контрарны.
Покажем, что отсюда следует, что они НЕ гомозиготны
... Но это же очевидно! Если не контрарны, то уж, конечно, не гомозиготны!
Мы пришли к противоречию, доказали, что не контрарные сепульки не
гомозиготны. Но тогда верно и ДРУГОЕ утверждение, что Если сепульки
гомозиготны, то они контрарны
Ю.Г.Карпов
Математическая логика и теория алгоритмов
35

36. Доказательство теорем. Использование эквивалентностей

Эквивалентность и импликации:
A B = (A B) & (B A)
Нужно доказать, что А тогда и только тогда, когда В
Доказательство проводится в два шага:
1. Доказываем (если А, то В) (прямая)
И
2. Доказываем (если В, то А) (обратная)
ИЛИ 2а. Доказываем (если НЕ А, то НЕ В)
РQ
P Q
Q P
P Q
00
1
1
1
01
1
0
0
10
0
1
0
11
1
1
1
Два доказательства = конъюнкция доказательств
Пример: Нужно доказать: Треугольник равносторонний тогда и только тогда,
когда все его углы равны (A B)
Доказательство этой теоремы проводится в два шага (прямая и обратная
теоремы):
1.
Если треугольник равносторонний, то все его углы равны (A B)
2.
Если все углы треугольника равны, то он равносторонний (B A)
Вместо теоремы A B - две простые: доказываем A B И доказываем B A
Ю.Г.Карпов
Математическая логика и теория алгоритмов
36

37. Доказательство теорем. Использование эквивалентностей

Сложная импликация: A (B &С) = (A B) & (А С)
A (B & С)
доказываются две более простые теоремы A B и А С
Вместо сложной теоремы
Пример: Доказать, что Если сеть Петри жива, то она ограничена и свободна
Доказываются две теоремы: Если сеть Петри жива, то она ограничена, И
Если сеть Петри жива, то она свободна
Ю.Г.Карпов
Математическая логика и теория алгоритмов
37

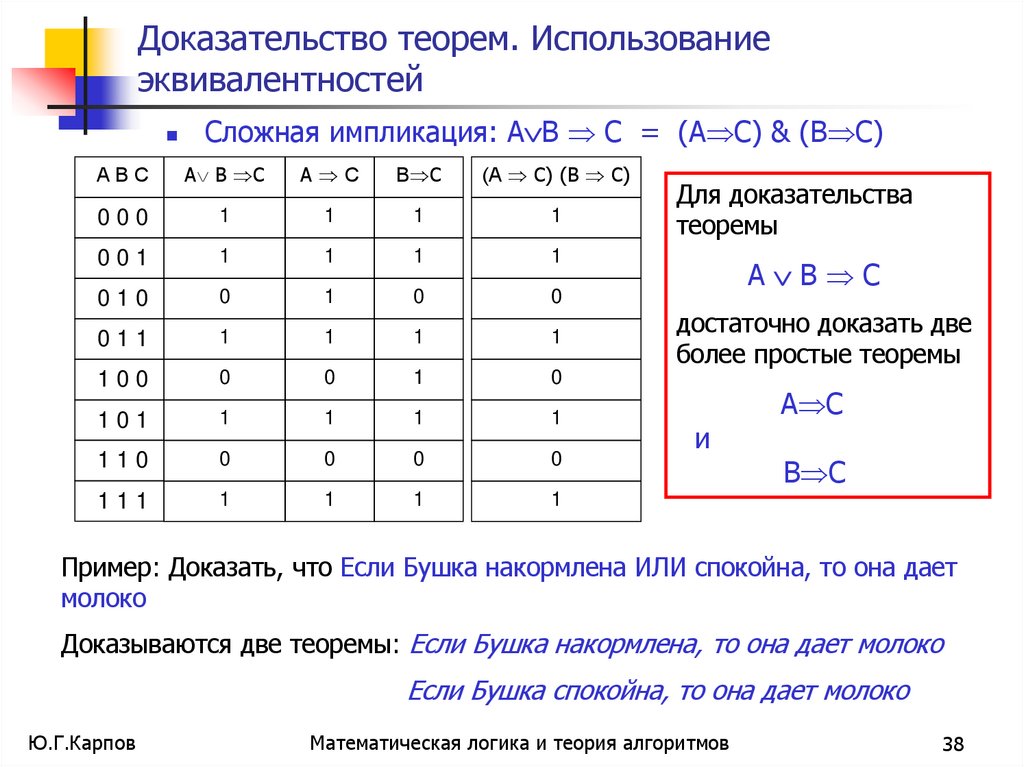
38. Доказательство теорем. Использование эквивалентностей

Сложная импликация: A В С = (A С) & (В С)
АВС
А В С
А С
В С
(А С) (B C)
000
1
1
1
1
001
1
1
1
1
010
0
1
0
0
011
1
1
1
1
100
0
0
1
0
101
1
1
1
1
110
0
0
0
0
111
1
1
1
1
Для доказательства
теоремы
A В С
достаточно доказать две
более простые теоремы
A С
и
В С
Пример: Доказать, что Если Бушка накормлена ИЛИ спокойна, то она дает
молоко
Доказываются две теоремы: Если Бушка накормлена, то она дает молоко
Если Бушка спокойна, то она дает молоко
Ю.Г.Карпов
Математическая логика и теория алгоритмов
38

39. Доказательство теорем. Необходимость и достаточность

А В
Фраза естественного языка
Формула
Если Р, то Q
Для Р необходимо Q
Q, если Р
Для P достаточно Q
Q, только если Р
P Q
P Q
P Q
Q P
Q P
А = Р, В = Q
А = P, В = Q
А = P, В = Q
А = Q, В = P
А = Q, В = P
Необходимым условием Р является Q
Достаточным условием P является Q
P Q
Q P
А = P, В = Q
А = Q, В = P
P Q
Р если и только если Q (еесли, iff)
Для Р необходимо и достаточно Q
P Q
Р тогда и только тогда, когда Q (ттогда) P Q
Как запомнить? Нужно ли запоминать?
Можно подставить два высказывания, одно из них явно более сильное,
чем второе. Например: А: равносторонний, В - равнобедренный
ЯСНО, что А В, но не наоборот (А более сильное утверждение)
Ю.Г.Карпов
Математическая логика и теория алгоритмов
39

40. Структура доказательства. Пример 1

Докажем теорему:
"Необходимым условием того, что сепульки не хроничны или не
бифуркальны, является то, что сепульки не являются одновременно и
хроничными, и бифуркальными”
Как доказать??
1 шаг: Выделяем атомарные высказывания
Х – сепулька хронична
Б – сепулька бифуркальна
2 шаг: Записываем структуру высказывания:
Теорема имеет структуру ( Х Б) (Х&Б)
По теореме де Моргана (Х&Б) = ( Х Б)
Итак, формулировка теоремы – тавтология А А!!
( Х Б) ( Х Б) - истина
Теорема доказана
Ю.Г.Карпов
Математическая логика и теория алгоритмов
40

41. Структура доказательства. Пример 2

Докажем теорему:
“ Для того, чтобы идеал был нильпотентным, необходимо и достаточно, чтобы он
был модулярным и радикальным”.
Как доказывать??
1 шаг: Выделение атомарных высказываний
Н – идеал нильпотентен; М – идеал модулярен; Р – идеал радикален
2 шаг: Запись структуры теоремы: Н М&Р
Доказательство разбивается на:
1) доказательство необходимости: для Н необходимо М и Р, т.е. Н МР
2) доказательство достаточности: для Н достаточно М и Р, т.е. МР Н
Но: Н МР = (Н М) & (Н Р ), или же, что то же ( М Н) & ( Р Н )
Таким образом, для доказательства исходной теоремы нам достаточно доказать ТРИ
теоремы, но более простые:
“Если идеал не модулярен, то он не нильпотентен”
( М Н) (от противного)
“Если идеал не радикален, то он не нильпотентен”
( Р Н) (от противного)
“Если идеал и модулярен, и радикален, то он нильпотентен” (М&Р Н)
Ю.Г.Карпов
Математическая логика и теория алгоритмов
41

42. Структура доказательства. Пример 3

Доказательство теоремы Поста:
“Для того, чтобы множество двоичных функций М было базисом, необходимо и
достаточно, чтобы в нем была по крайней мере одна функция, не сохраняющая 0,
по крайней мере одна функция, не сохраняющая 1, ... ”.
Как доказывали??
1 шаг: Выделяли атомарные высказывания
Бм – множество М - базис;
Ао = М М0 – в М входят только функции, сохраняющие 0,
А1 = М М1 – в М входят только функции, сохраняющие 1,
Ас = М Мс – в М входят только самодвойственные функции,
Ам = М Мм – в М входят только монотонные функции,
Ал = М Мл – в М входят только линейные функции
2 шаг: записывали структуры теоремы:
Теорема имеет структуру Бм ( Ао & А1 & Аc & Ам & Ал)
Ю.Г.Карпов
Математическая логика и теория алгоритмов
42

43. Структура доказательства теоремы Поста

Доказательство теоремы Поста:
“Для того, чтобы множество двоичных функций М было базисом, необходимо и
достаточно, чтобы в нем была по крайней мере одна функция, не сохраняющая 0,
по крайней мере одна функция, не сохраняющая 1, ... ”.
Как доказывали??
Теорема имеет структуру Бм ( Ао & А1 & Аc & Ам & Ал)
Доказательство было разбито на:
доказательство необходимости: Бм ( Ао & А1 & Аc & Ам & Ал)
доказательство достаточности: ( Ао & А1 & Аc & Ам & Ал) Бм
Как доказывали необходимость?
Бм ( Ао & А1 & Аc & Ам & Ал) = (Бм Ао) & ... & (Бм Ал)
Каждую теорему доказывали от противного:
(Ао Бм) & (А1 Бм) & (Ас Бм) & (Ам Бм) & (Ал Бм)
Как доказывали достаточность?
Достаточность доказывали конструктивно: строили функции базиса НЕ и И
из функций, удовлетворяющих условию Ао, и А1, и Аc, и Ам, и Ал
Ю.Г.Карпов
Математическая логика и теория алгоритмов
43

44. Логическое следствие

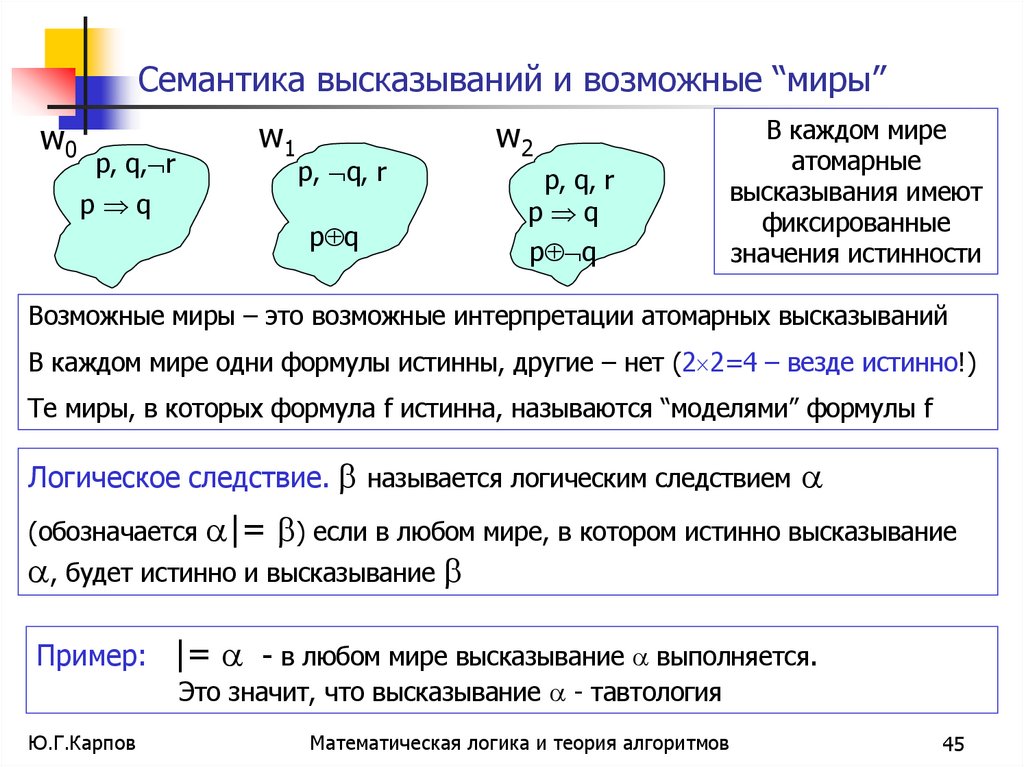
45. Семантика высказываний и возможные “миры”

w0
p, q, r
w1
p, q, r
p q
p q
w2
p, q, r
p q
p q
В каждом мире
атомарные
высказывания имеют
фиксированные
значения истинности
Возможные миры – это возможные интерпретации атомарных высказываний
В каждом мире одни формулы истинны, другие – нет (2 2=4 – везде истинно!)
Те миры, в которых формула f истинна, называются “моделями” формулы f
Логическое следствие. называется логическим следствием
(обозначается |= ) если в любом мире, в котором истинно высказывание
, будет истинно и высказывание
Пример: |= - в любом мире высказывание выполняется.
Это значит, что высказывание - тавтология
Ю.Г.Карпов
Математическая логика и теория алгоритмов
45

46. Логическое следствие

Проверка того, что некоторое высказывание является логическим
следствием нескольких других высказываний, является одной из главных
задач логики.
Мы рассмотрим максимальное следствие из фактов F1, F2, ..., Fn
Максимально сильным следствием из фактов F1, ..., Fn является
конъюнкция этих фактов
Пример. Дело о рецидивистах.
Трое рецидивистов, А, В и С, подозреваются в преступлении. Неопровержимо
установлены следующие факты:
(F1) Если А виновен, а В невиновен, то в деле участвовал С;
(F2) С никогда не действует в одиночку;
(F3) А всегда ходит на дело один;
(F4) Никто, кроме А, В и С в преступлении не замешан, но, по крайней мере, один из
этой тройки виновен
Какие выводы можно сделать на основании этих фактов?
Ю.Г.Карпов
Математическая логика и теория алгоритмов
46

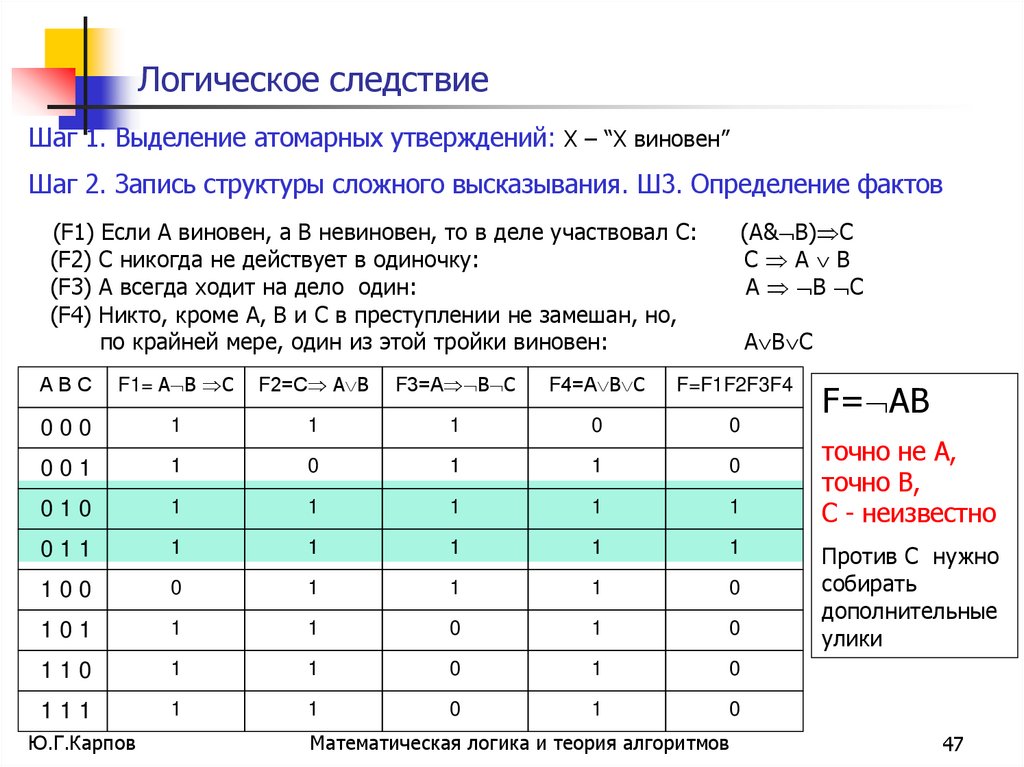
47. Логическое следствие

Шаг 1. Выделение атомарных утверждений: Х – “Х виновен”
Шаг 2. Запись структуры сложного высказывания. Ш3. Определение фактов
(F1) Если А виновен, а В невиновен, то в деле участвовал С:
(F2) С никогда не действует в одиночку:
(F3) А всегда ходит на дело один:
(F4) Никто, кроме А, В и С в преступлении не замешан, но,
по крайней мере, один из этой тройки виновен:
(А& В) С
С А В
А В С
А В С
АВС
F1= А В С
F2=С А В
F3=А В С
F4=А В С
F=F1F2F3F4
000
1
1
1
0
0
001
1
0
1
1
0
010
1
1
1
1
1
011
1
1
1
1
1
100
0
1
1
1
0
101
1
1
0
1
0
110
1
1
0
1
0
111
1
1
0
1
0
Ю.Г.Карпов
Математическая логика и теория алгоритмов
F= АВ
точно не А,
точно В,
С - неизвестно
Против С нужно
собирать
дополнительные
улики
47

48. Максимально сильное следствие

Задача Р. Смаллиана
Друг спросил меня:
Правда ли, что если ты любишь Пэт, то ты также любишь Квинси?"
На это я ответил:
Если это правда, то я люблю Пэт, и если я люблю Пэт, то это правда"
Кого я люблю в действительности?
Обозначим П – Я люблю Пэт, К- Я люблю Квинси
Вопрос: В= (П К)
Полученная информация: F = (В П) & (П В)
ПК
В=(П К) f1=В П
f2=П В
F=f1&f2
00
1
0
1
0
01
1
0
1
0
10
0
1
0
0
11
1
1
1
1
Ю.Г.Карпов
F=П К
Вывод:
Любит обеих
Математическая логика и теория алгоритмов
48

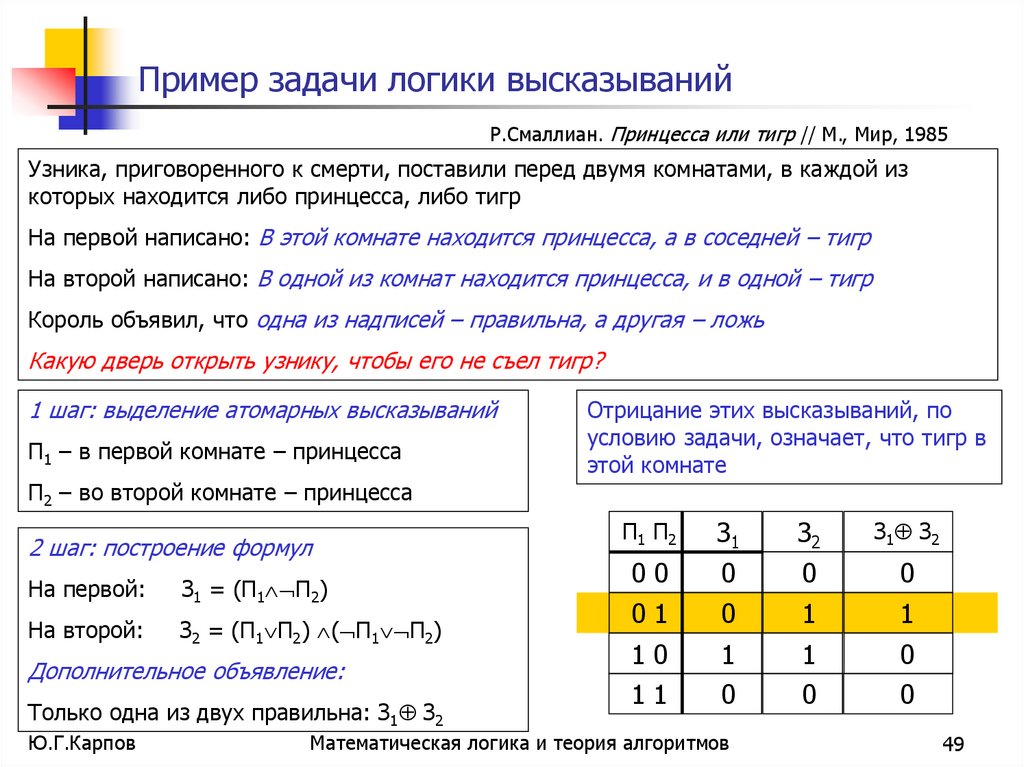
49. Пример задачи логики высказываний

Р.Смаллиан. Принцесса или тигр // М., Мир, 1985
Узника, приговоренного к смерти, поставили перед двумя комнатами, в каждой из
которых находится либо принцесса, либо тигр
На первой написано: В этой комнате находится принцесса, а в соседней – тигр
На второй написано: В одной из комнат находится принцесса, и в одной – тигр
Король объявил, что одна из надписей – правильна, а другая – ложь
Какую дверь открыть узнику, чтобы его не съел тигр?
1 шаг: выделение атомарных высказываний
П1 – в первой комнате – принцесса
П2 – во второй комнате – принцесса
2 шаг: построение формул
На первой:
З1 = (П1 П2)
На второй:
З2 = (П1 П2) ( П1 П2)
Дополнительное объявление:
Только одна из двух правильна: З1 З2
Ю.Г.Карпов
Отрицание этих высказываний, по
условию задачи, означает, что тигр в
этой комнате
П1 П2
З1
З2
З1 З2
00
0
0
0
01
0
1
1
10
1
1
0
11
0
0
0
Математическая логика и теория алгоритмов
49

50. Решение логических задач: инспектор в психбольнице (Р. Смаллиан)

Инспектора Крейга из Скотланд-Ярда направили для проверки лечебницы
для умалишенных. Каждый из обитателей лечебницы - врач либо пациент
- мог быть либо здоров, либо лишен рассудка. Если он был здоров, то
говорил правду, если лишен рассудка, то только лгал
Крейг побеседовал с двумя обитателями лечебницы, Джонсом и Смитом.
Джонс сказал, что Смит - один из врачей больницы, а Смит сказал, что
Джонс - пациент. Крейг понял, что дело нечисто!
ПОЧЕМУ???
Обозначим:
Дсм – Смит – доктор
(тогда Дсм – Смит – пациент)
Нсм – Смит – нормален (тогда Hсм – Смит – псих)
Ддж – Джонс – доктор
(тогда Ддж – Джонс – пациент)
Ндж – Джонс – нормален (тогда Hдж – Джонс – псих)
Информация от Джонса: Дсм
Информация от Смита: Ддж
Использование условия, что нормальный говорит правду, а псих – лжет:
Ндж Дсм, Ндж Дсм, Нсм Ддж, Нсм Ддж
Ю.Г.Карпов
Математическая логика и теория алгоритмов
50

51. Решение логических задач: инспектор в психбольнице (II)

Вся полученная информация – это конъюнкция всех тех утверждений,
которые мы считаем верными:
F = (Ндж Дсм)&( Ндж Дсм)&(Нсм Ддж)&( Нсм Ддж)
Что можно извлечь из всей этой информации?
Преобразуем в ДНФ:
F = (Ндж Дсм)&( Ндж Дсм)&(Нсм Ддж)&( Нсм Ддж) =
( Ндж Дсм)&(Ндж Дсм)&( Нсм Ддж)&(Нсм Ддж) =
( Ндж Дсм Дсм Ндж ) & ( Нсм Ддж Ддж Нсм ) =
Ндж Дсм Нсм Ддж
Ндж Дсм Нсм Ддж
Ндж Дсм Нсм Ддж
Ндж Дсм Нсм Ддж
Джонс доктор, но ненормален
Смит пациент, но нормален
Смит доктор, но ненормален
Джонс пациент, но нормален
Что-либо из этого обязательно есть. Нужно расследование
Ю.Г.Карпов
Математическая логика и теория алгоритмов
51

52. Решение логических задач. Правдивые и лгуны

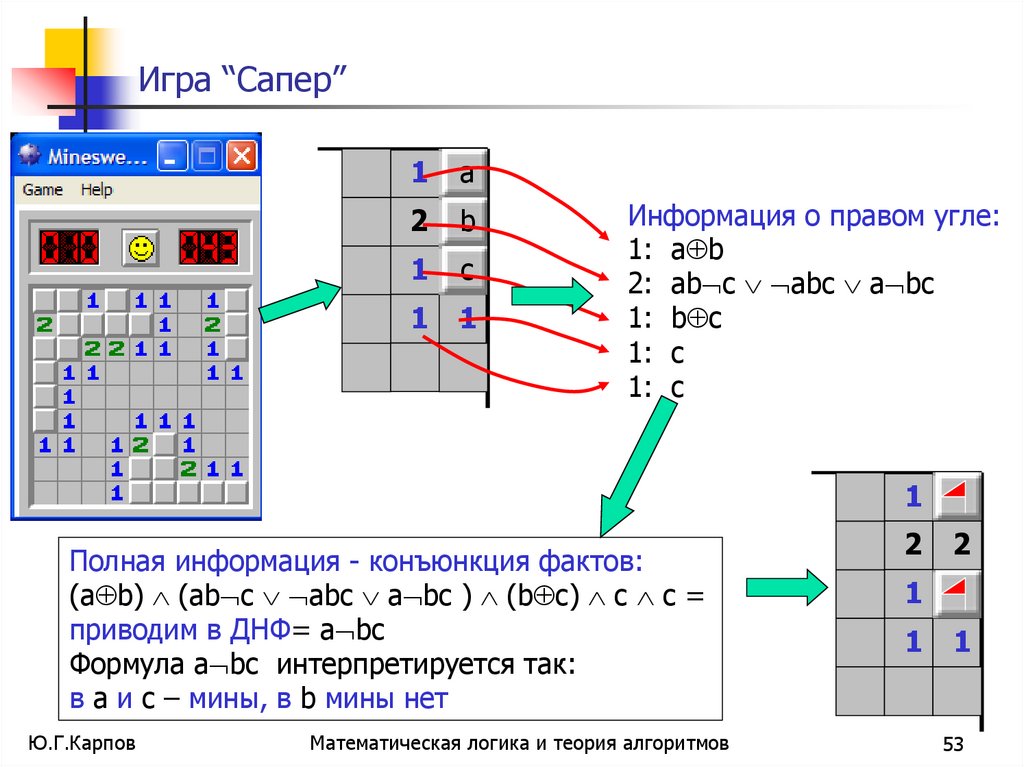
Игра “Сапер”
1
a
2
b
1
c
1
1
Информация о правом угле:
1: a b
2: ab c abc a bc
1: b c
1: c
1: c
1
Полная информация - конъюнкция фактов:
(a b) (ab c abc a bc ) (b c) c c =
приводим в ДНФ= a bc
Формула a bc интерпретируется так:
в а и c – мины, в b мины нет
Ю.Г.Карпов
Математическая логика и теория алгоритмов
2
2
1
1
1
53

53. Игра “Сапер”

Примеры задач
По известным фактам вывести формулу, определяющую, где находятся мины
a b
с d
Ю.Г.Карпов
Решение :
Полная информация:
(a c) (c d) =
Приводим в ДНФ:
(a c ac) (с d cd) =
a cd ac d
Мины либо в а и d, либо в с. Есть ли мина в b - неизвестно
Математическая логика и теория алгоритмов
54

54. Примеры задач

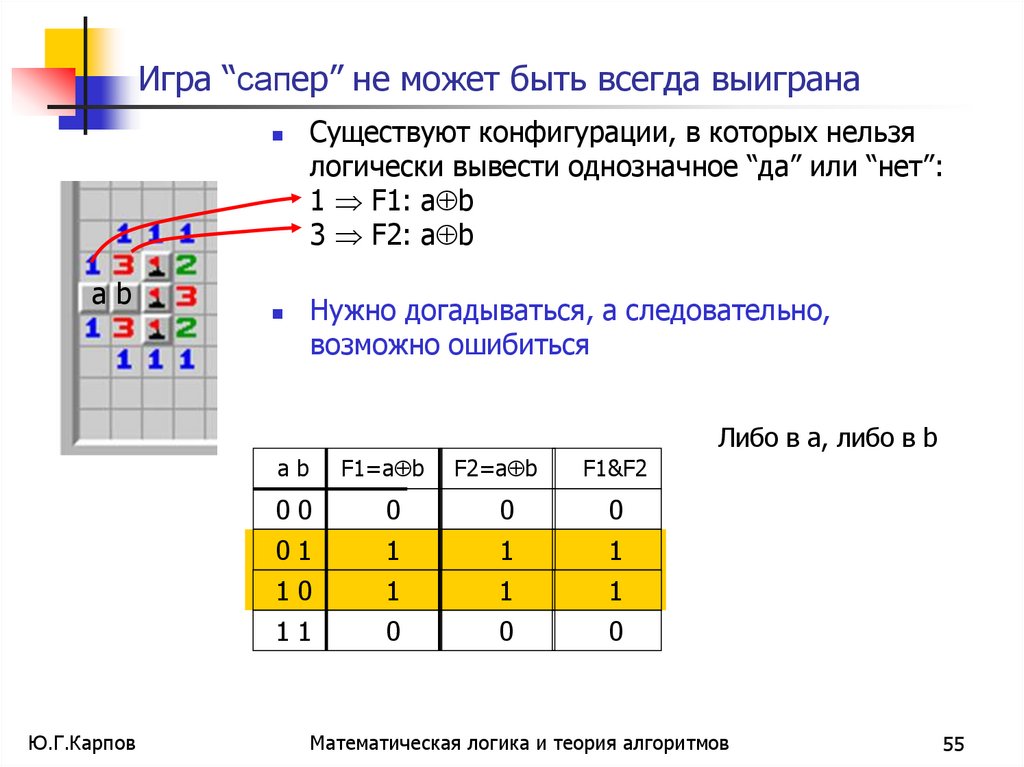
Игра “сапер” не может быть всегда выиграна
ab
Существуют конфигурации, в которых нельзя
логически вывести однозначное “да” или “нет”:
1 F1: a b
3 F2: a b
Нужно догадываться, а следовательно,
возможно ошибиться
Либо в а, либо в b
Ю.Г.Карпов
ab
F1=a b
F2=a b
F1&F2
00
0
0
0
01
1
1
1
10
1
1
1
11
0
0
0
Математическая логика и теория алгоритмов
55

55. Игра “сапер” не может быть всегда выиграна

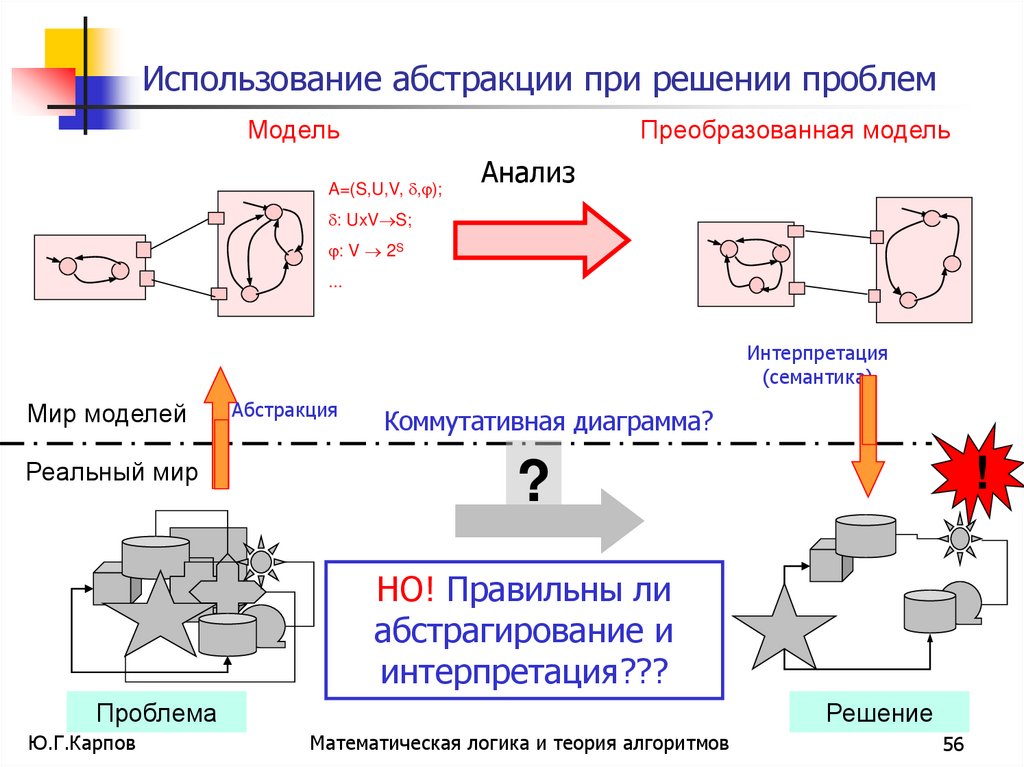
Использование абстракции при решении проблем
Модель
Преобразованная модель
A=(S,U,V, , );
Анализ
: UxV S;
: V 2S
...
Интерпретация
(семантика)
Мир моделей
Реальный мир
Абстракция
Коммутативная диаграмма?
!
?
НО! Правильны ли
абстрагирование и
интерпретация???
Проблема
Ю.Г.Карпов
Решение
Математическая логика и теория алгоритмов
56

56. Использование абстракции при решении проблем

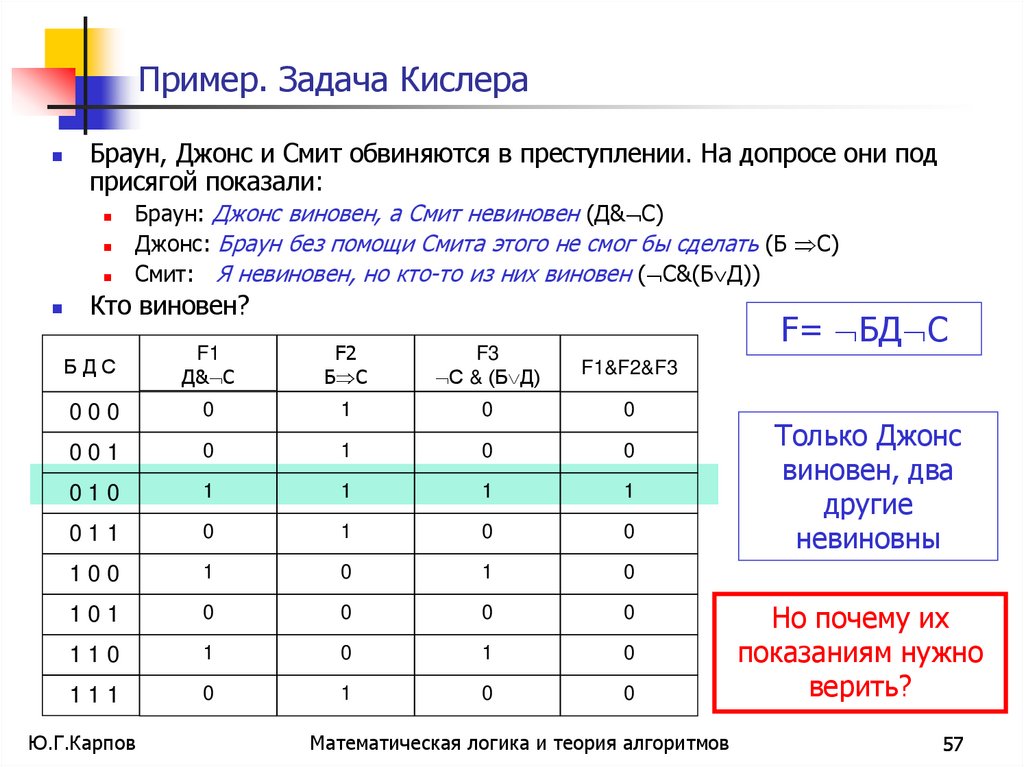
Пример. Задача Кислера
Браун, Джонс и Смит обвиняются в преступлении. На допросе они под
присягой показали:
Браун: Джонс виновен, а Смит невиновен (Д& С)
Джонс: Браун без помощи Смита этого не смог бы сделать (Б С)
Смит: Я невиновен, но кто-то из них виновен ( C&(Б Д))
Кто виновен?
F= БД С
БДС
F1
Д& C
F2
Б С
F3
С & (Б Д)
F1&F2&F3
000
0
1
0
0
001
0
1
0
0
010
1
1
1
1
011
0
1
0
0
100
1
0
1
0
101
0
0
0
0
110
1
0
1
0
111
0
1
0
0
Ю.Г.Карпов
Математическая логика и теория алгоритмов
Только Джонс
виновен, два
другие
невиновны
Но почему их
показаниям нужно
верить?
57

57. Пример. Задача Кислера

(2)
На допросе под присягой показали:
Браун: Джонс виновен, а Смит невиновен (Д& С)
Джонс: Браун без помощи Смита этого не смог бы сделать (Б С)
Смит: Я не виноват, но кто-то из них виновен ( C&(Б Д))
НО ЯВЛЯЮТСЯ ЛИ ИХ СЛОВА ПРАВДОЙ???
Предположим, что невиновный говорит правду (под присягой!), а
виновный – лжет. Тогда факты, которые мы считаем истинными, будут
выглядеть по-другому:
F1 = ( Б (Д & С))
& ( Б (Д & С))
(если виновен, то врет!)
F2 = ( Д (Б С))
& ( Д (Б С))
(если виновен, то врет!)
F3 = ( С ( С&(Б Д ))) & ( С ( С & (Б Д)) ) (если виновен, то врет!)
Результат, полученный с помощью формального анализа, будет
совершенно другим для этих фактов!
Ю.Г.Карпов
Математическая логика и теория алгоритмов
58

58. Пример. Задача Кислера (2)

Неоднозначность формализации
Нельзя считать, что для практических задач можно сразу
использовать формальный аппарат и легко получить решение
При использовании формального аппарата для решения реальных
задач, формализация должна быть адекватной! Различные
абстрагирования могут привести к совершенно различным ответам
в одной и той же задаче
Пример. Задача Рэймонда Смаллиана из книги “Принцесса или тигр”.
Узнику, приговоренному к смерти, король дал шанс спастись. Узника
подвели к двум комнатам, в каждой из которых может оказаться либо
принцесса, либо тигр. На каждой из комнат прикреплены таблички. На
первой (Т1) написано: Что выбрать – большая разница. На второй (Т2):
Лучше выбрать другую комнату. ...
Как формализовать высказывание Лучше выбрать другую комнату?
Первый вариант: T2: П2
(в этой комнате нет принцессы)
Второй вариант: T2: П1
(принцесса в другой комнате)
В общем случае разные варианты формализации могут привести к
разным результатам формального анализа
Ю.Г.Карпов
Математическая логика и теория алгоритмов
59

59. Неоднозначность формализации

Заключение
Логика – это абстрактная теория, позволяющая анализировать законы
мышления, выполнять рассуждения, делать правильные выводы
Логика высказываний оперирует формулами, построенными из атомов
(простейших утверждений), каждый из которых может быть либо
истинным, либо ложным. Нас обычно интересует истинность сложных
утверждений, если известна истинность составляющих их атомарных
утверждений
В формальной логике мы фиксируем только форму, структуру
рассуждений и абстрагируемся от семантики, смысла фраз, анализируя
только одну смысловую составляющую высказываний – их истинностное
значение (Истина или Ложь)
Операции логики совпадают с операциями булевых функций
Примеры применения логики
- проверка эквивалентности высказываний
- анализ структуры доказательства теорем
- логическое следствие - проверка того, что некоторое высказывание
является следствием нескольких других высказываний, истинность
которых предполагается заданной
При использовании формального аппарата для решения проблем
нужно выбирать адекватную модель
Ю.Г.Карпов
Математическая логика и теория алгоритмов
60

60. Заключение

Персоналии
Аристотель (~350 г ВС) впервые сформулировал логическую
систему
Г.Лейбниц (1646-1717) предложил строить логику на формальной
основе с использованием символических обозначений
Джордж Буль (1815-1864) – создал булеву алгебру (которая стала
основой теории двоичных чисел) именно как метод
математического анализа логических утверждений. С его книги
1847г. «Математический анализ логики» началась математическая
логика
Работы Г.Шеффера – (Henry M.Sheffer США) Ч. Пирса (Charles
Sanders Pierce) в 1880 г. и Аугустуса Де Моргана (Augustus De
Morgan) 1850-е – были посвящены именно логике, анализу
логических утверждений
Людвиг Витгенштейн (1889-1951), австрийский философ и логик,
придумал таблицы истинности
Ю.Г.Карпов
Математическая логика и теория алгоритмов
61

61. Персоналии

Дополнения

62. Дополнения

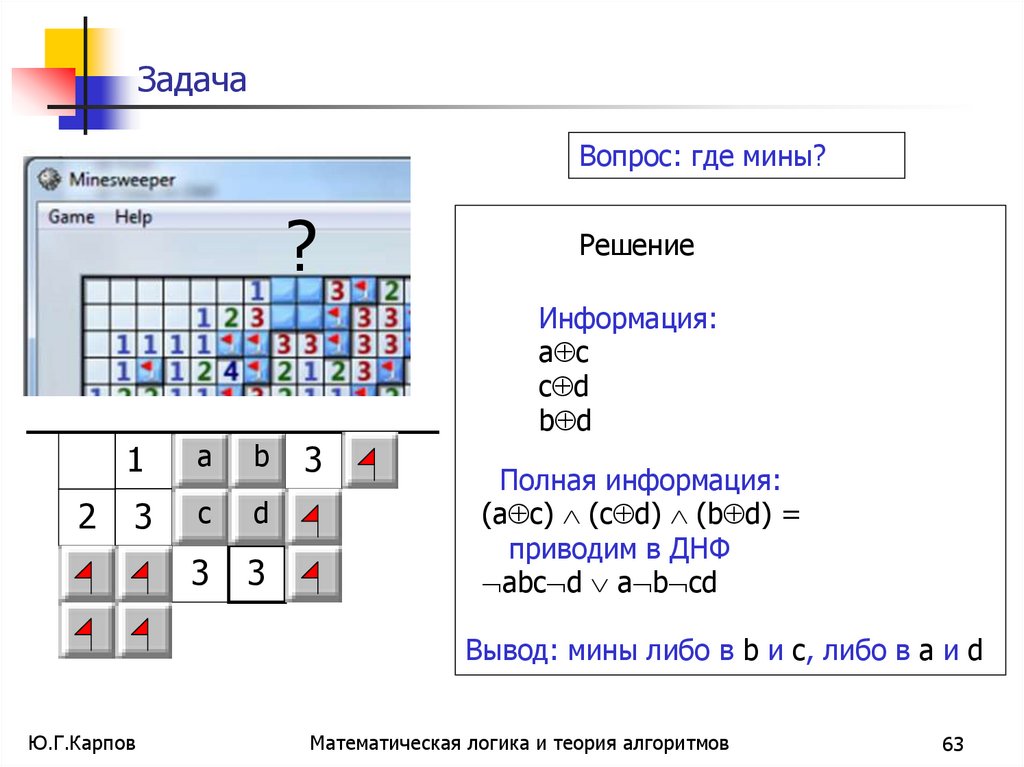
Задача
Вопрос: где мины?
?
Решение
Информация:
a с
c d
b d
2
1
a
b
3
c
d
3
3
3
Полная информация:
(a с) (c d) (b d) =
приводим в ДНФ
abc d a b cd
Вывод: мины либо в b и c, либо в a и d
Ю.Г.Карпов
Математическая логика и теория алгоритмов
63

63. Задача

Спасибо за внимание
Ю.Г.Карпов
Математическая логика и теория алгоритмов
65