Лекция 10 Многомерная случайная оптимизация 2

1.

Тема: МНОГОМЕРНАЯ СЛУЧАЙНАЯ
ОПТИМИЗАЦИЯ
2024 г.

2. 1. Постановка задачи. Метод слепого поиска

Идея метода слепого поиска
Случайным образом «кидаем» в пространство Rn M точек.
Выбираем точку с наименьшим значением целевой функции.
Если ищем минимум в D Rn (задача условной оптимизации),
то выбираем точку с наименьшим значением целевой
функции среди точек, попавших в D

3. Метод слепого поиска

Преимущества метода
• Легко алгоритмизируется
• Функция может быть любой
• Глобальный минимум! При удачном выборе области
поиска
Недостатки метода
• Проблема первоначального выбора области поиска
• Как достичь требуемую точность?
• При больших М работает медленно
Модификация метода
Выбираем область поиска, проводим первую итерацию
метода, находим лучшую точку. Выбираем новую область
поиска вблизи лучшей точки, проводим новую итерацию в
этой области, находим лучшую точку и т.д.
? Когда остановиться?

4. 2. Метод случайных направлений. Идея

При решении задачи (1) методом случайных направлений
используется следующая итерационная формула:
!!!
Могут быть получены разные модификации метода в
зависимости от того, как изменяется шаг и какие действия
будут выполняться при неудачной попытке.

5. 2. Метод случайных направлений. Алгоритм метода с возвратом при неудачном шаге

6. 2. Метод случайных направлений. Алгоритм метода с возвратом при неудачном шаге

7. 2. Метод случайных направлений. Условие прекращения вычислений

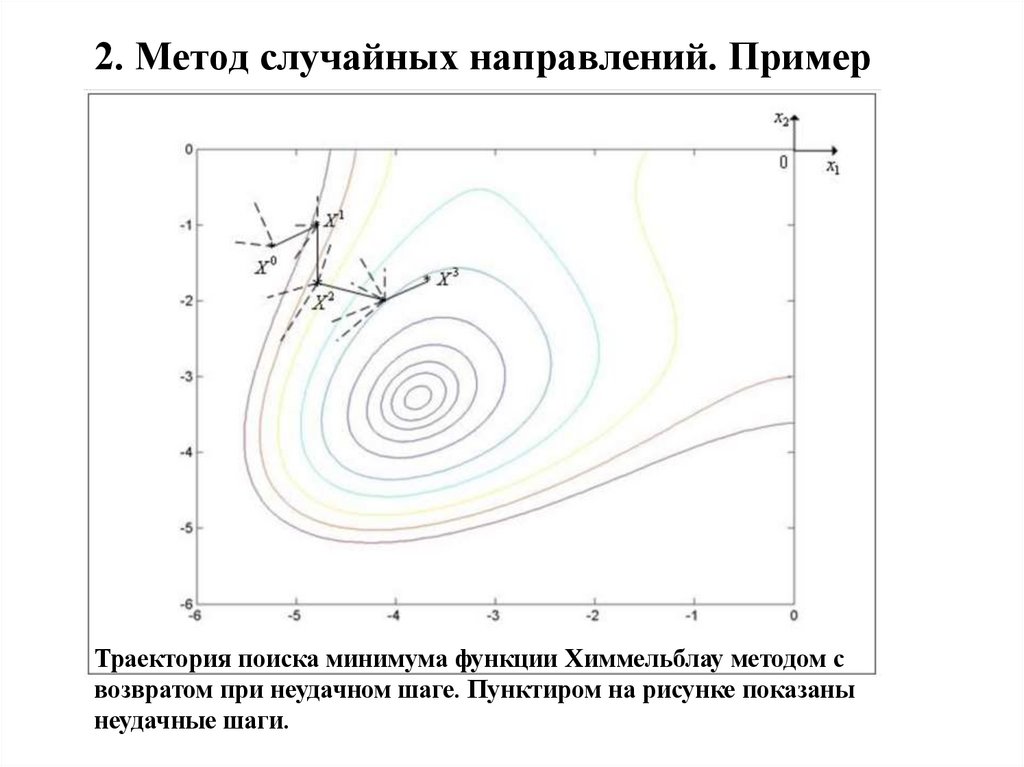
8. 2. Метод случайных направлений. Пример

Траектория поиска минимума функции Химмельблау методом с
возвратом при неудачном шаге. Пунктиром на рисунке показаны
неудачные шаги.

9. 2. Метод случайных направлений. Преимущества и недостатки

Преимущества метода
• Не требует вычисления производных
Недостатки метода
• Не факт, что найдем глобальный минимум
• Проблема выбора начальной точки
• «Овраги» могут быстро уменьшить шаг, и метод будет
работать медленно
Модификация метода
Откат на шаг назад
Метод наилучшей пробы: на каждой итерации выбираем
несколько случайных направлений и идем туда, где значение
функции получилось меньше всего.
Метод поиска с «наказанием случайностью». На всех
итерациях, начиная со второй, сначала пробуем сделать шаг в
том же направлении, что и на предыдущей итерации.

10. 2. Метод случайных направлений в задачах условной оптимизации

Что изменится, если в задаче есть условия?
В новую точку можно переходить только в том случае, если
она удовлетворяет ограничениям задачи.
Поэтому: не учитывать отказы из-за выхода за границу области
допустимых решений.
Подумать: а если экстремум будет на границе области? Не
будет ли проблем?
Проблема: ограничения-равенства