9df75a9735944d7cb48684fe93c2480d

1.

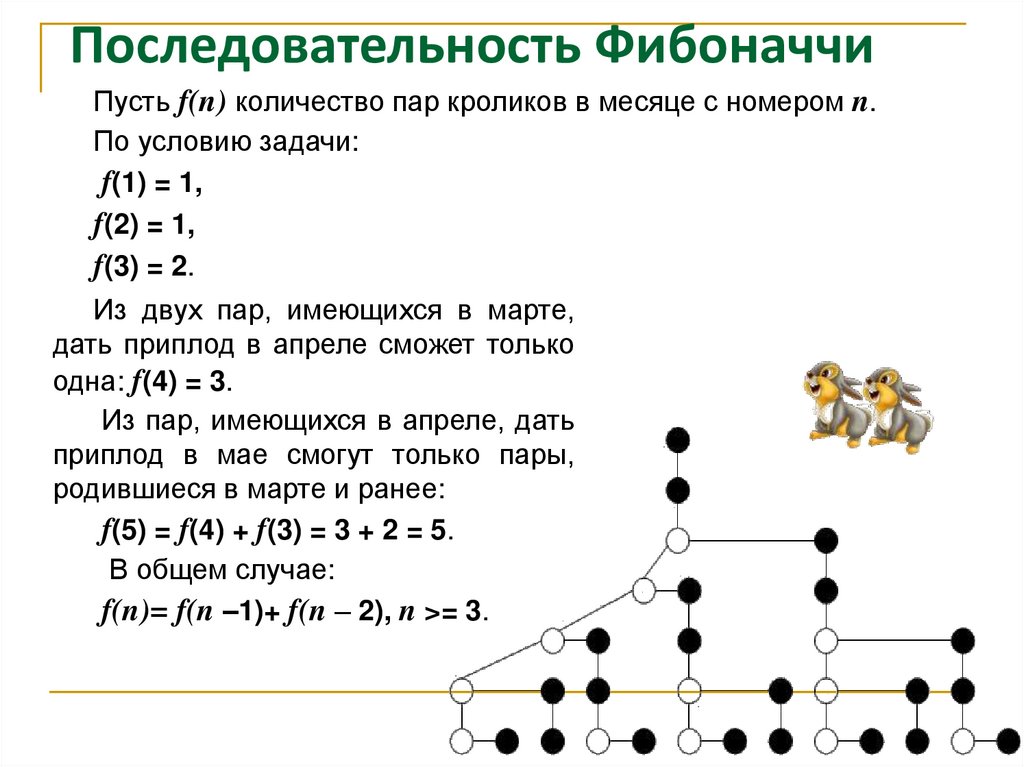
Последовательность Фибоначчи
Пусть f(n) количество пар кроликов в месяце с номером n.
По условию задачи:
f(1) = 1,
f(2) = 1,
f(3) = 2.
Из двух пар, имеющихся в марте,
дать приплод в апреле сможет только
одна: f(4) = 3.
Из пар, имеющихся в апреле, дать
приплод в мае смогут только пары,
родившиеся в марте и ранее:
f(5) = f(4) + f(3) = 3 + 2 = 5.
В общем случае:
f(n)= f(n –1)+ f(n – 2), n >= 3.

2. Подобного типа задачи, когда происходит обращение функции к самой себе, называется Рекурсия

Алгоритм вычисления значения функции F(n), где n –
натуральное число,
задан следующими соотношениями:
F(1) = 1
F(n) = F(n–1) * n, при n > 1
Чему равно значение функции F(5)?
В ответе запишите только натуральное число.
Подобного типа задачи, когда происходит обращение
функции к самой себе, называется Рекурсия
Как это реализовать?

3.

Функция
function f (n: integer): integer;
begin
if (n=1) or (n=2) then f:=1
else f:=f(n-1)+f(n-2)
end;
Полученная функция рекурсивная - в ней реализован
способ вычисления очередного значения функции через
вычисление её предшествующих значений.
3 3 3 3 3 ...