11_Rot_Pl_25

1. DESKRIPTÍVNA GEOMETRIA

Prednáška 11
Obsah
PLOCHY
základné vlastnosti
rozdelenie
ROTAČNÉ PLOCHY
základné vlastnosti
rez všeobecnej rotačnej plochy
rotačné plochy 2. stupňa a ich rezy

2.

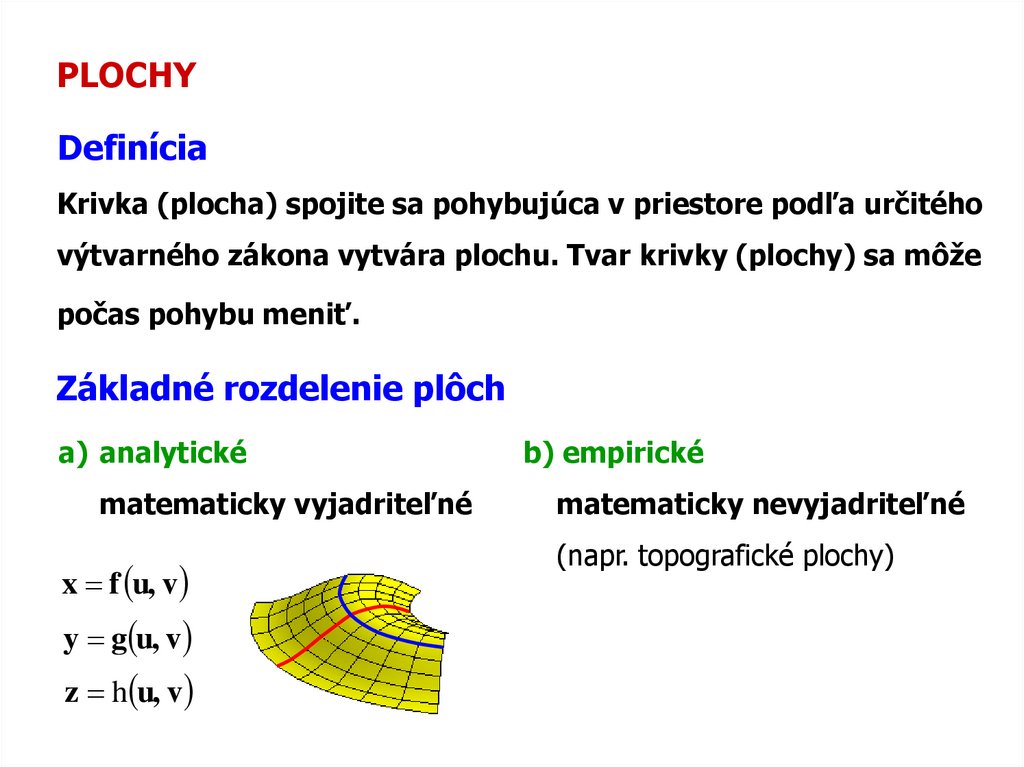
PLOCHY
Definícia
Krivka (plocha) spojite sa pohybujúca v priestore podľa určitého
výtvarného zákona vytvára plochu. Tvar krivky (plochy) sa môže
počas pohybu meniť.
Základné rozdelenie plôch
a) analytické
matematicky vyjadriteľné
x f u, v
y g u, v
z h u, v
b) empirické
matematicky nevyjadriteľné
(napr. topografické plochy)

3.

Ďalšie rozdelenie plôch
1. Podľa tvoriacej čiary
3. Grafické plochy – určené
- priamkové
sústavou rezov alebo sieťou
- cyklické
bodov
atď
2. Podľa druhu pohybu
4. Interpolačné plochy –
- rotačné
určené sieťou bodov alebo
- translačné
okrajovými krivkami
- skrutkové
- Coonsove
atď.
- Bezierove
- Fergusonove
atď

4.

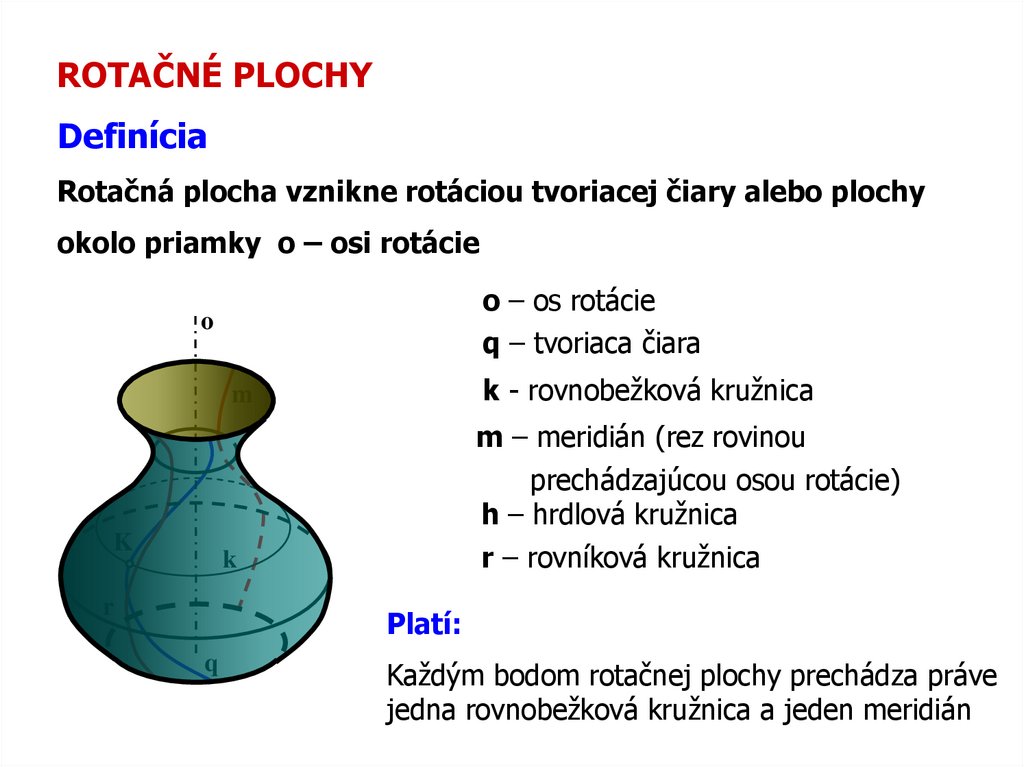
ROTAČNÉ PLOCHY
Definícia
Rotačná plocha vznikne rotáciou tvoriacej čiary alebo plochy
okolo priamky o – osi rotácie
o – os rotácie
q – tvoriaca čiara
o
m
k - rovnobežková kružnica
k
m – meridián (rez rovinou
prechádzajúcou osou rotácie)
h – hrdlová kružnica
r – rovníková kružnica
h
K
T
r
Platí:
q
q
Každým bodom rotačnej plochy prechádza práve
jedna rovnobežková kružnica a jeden meridián

5.

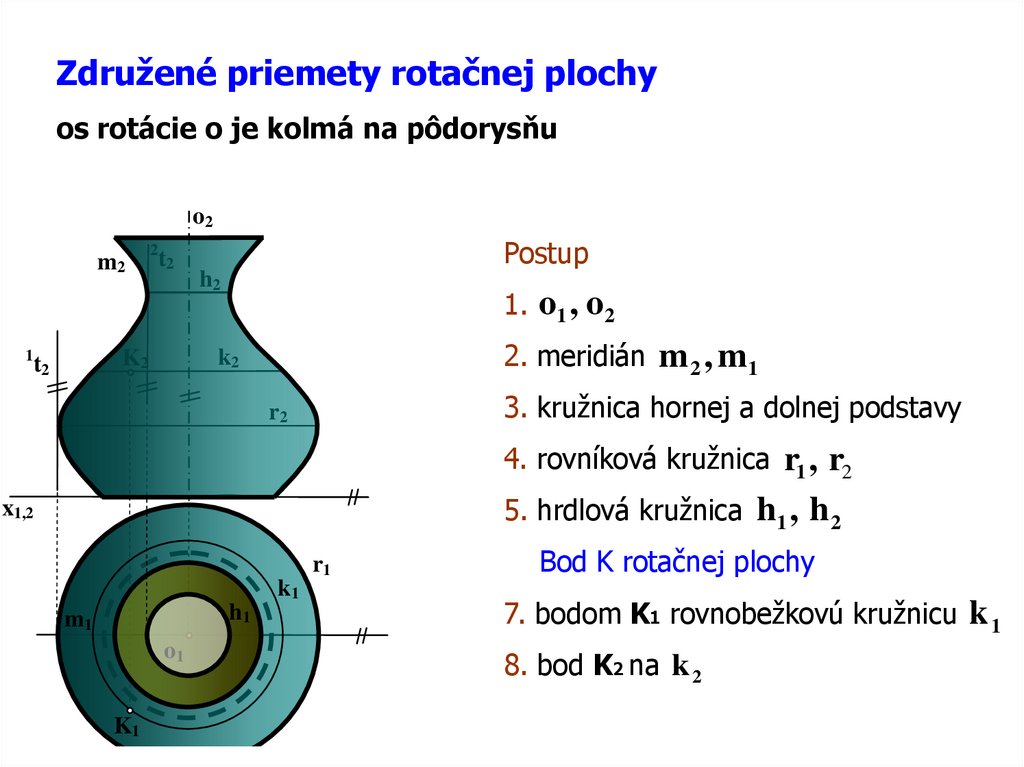
Združené priemety rotačnej plochy
os rotácie o je kolmá na pôdorysňu
o22
m2
1
2
t2
h2
1. o1 , o 2
2. meridián m 2 , m1
k2
K2
t2
Postup
3. kružnica hornej a dolnej podstavy
r2
4. rovníková kružnica r1 , r2
5. hrdlová kružnica h1 , h 2
x1,2
r1
k1
h1
m1
o11
K1
Bod K rotačnej plochy
7. bodom K1 rovnobežkovú kružnicu k 1
8. bod K2 na k 2

6.

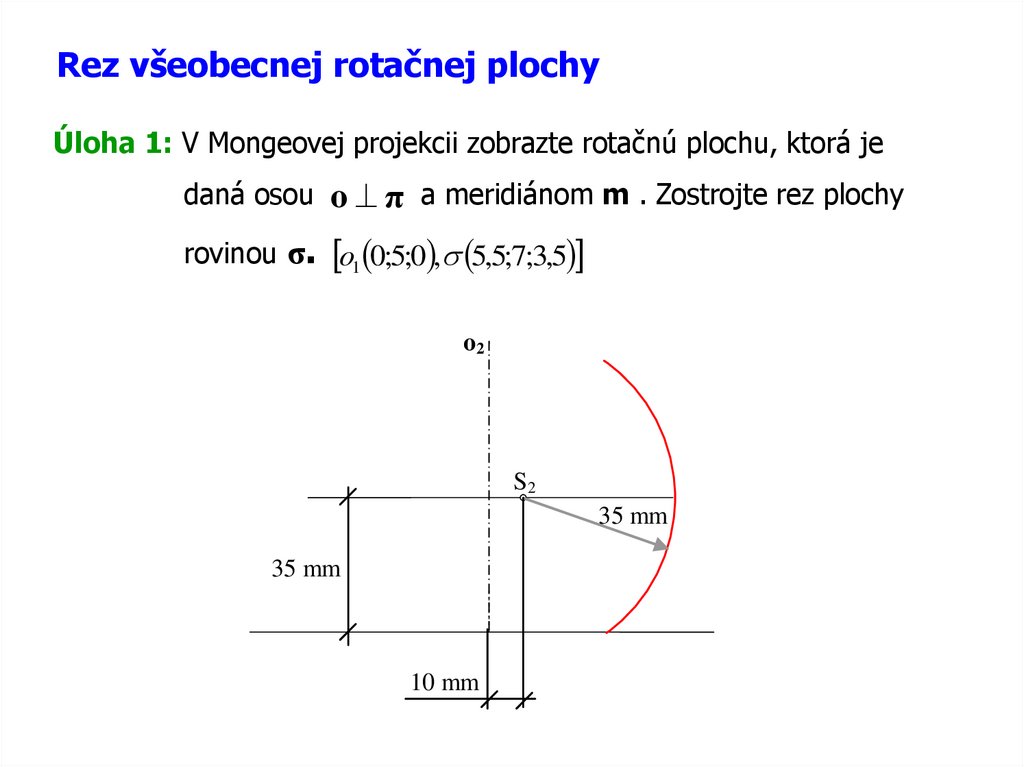
Rez všeobecnej rotačnej plochy
Úloha 1: V Mongeovej projekcii zobrazte rotačnú plochu, ktorá je
daná osou o π a meridiánom m . Zostrojte rez plochy
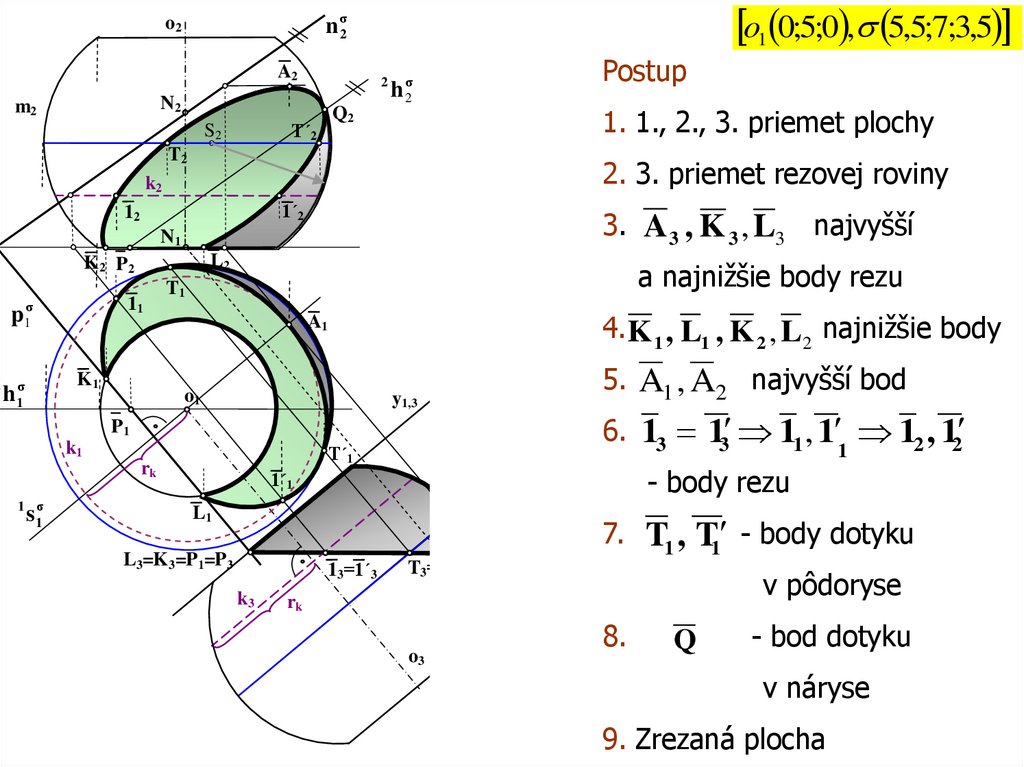
rovinou σ. o1 0;5;0 , 5,5;7;3,5
o2
S2
35 mm
35 mm
x1,2
10 mm

7.

22
A22
22
N22
m
m22
o1 0;5;0 , 5,5;7;3,5
n σ2σ2
o22
Q22
T´22
35 mm
S22
T22
h σ2σ2
1´22
122
3. A 3 , K 3 , L3
N11
p1σ1σ
h 1σ1σ
L22
K
K22 P 22
10 mm
T11
111
K
K11
4. K 1 , L1 , K 2 , L2 najnižšie body
A11
o11
y1,3
1,3
kk11
T´11
rkk
s
o33
najvyšší
a najnižšie body rezu
P 11
11 σσ
11
1. 1., 2., 3. priemet plochy
2. 3. priemet rezovej roviny
k22
35 mm
Postup
5. A1 , A2 najvyšší bod
6. 13 13 11 , 1 12 , 12
1
- body rezu
1´11
L11
L
L33=K 33=P 11=P 33
133=1´33
k33
N33 A33
σ33
T33=T´33
7. T1 , T1 - body dotyku
v pôdoryse
rkk
o33
8.
Q
- bod dotyku
v náryse
9. Zrezaná plocha

8.

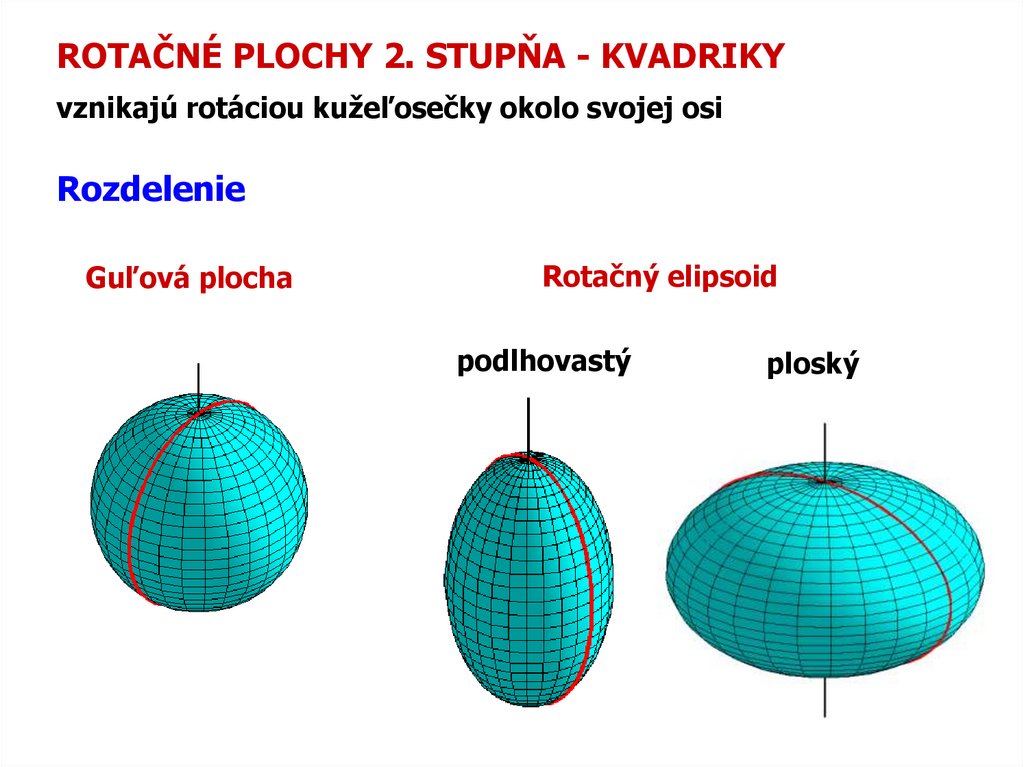
ROTAČNÉ PLOCHY 2. STUPŇA - KVADRIKY
vznikajú rotáciou kužeľosečky okolo svojej osi
Rozdelenie
Guľová plocha
Rotačný elipsoid
podlhovastý
ploský

9.

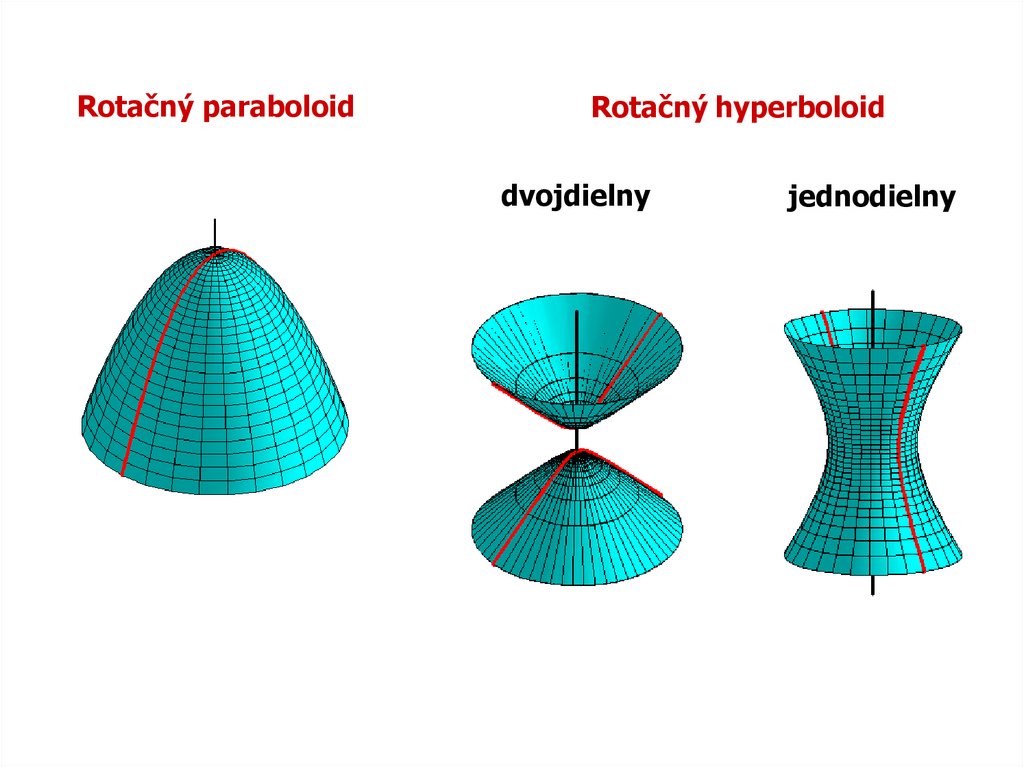
Rotačný paraboloid
Rotačný hyperboloid
dvojdielny
jednodielny

10.

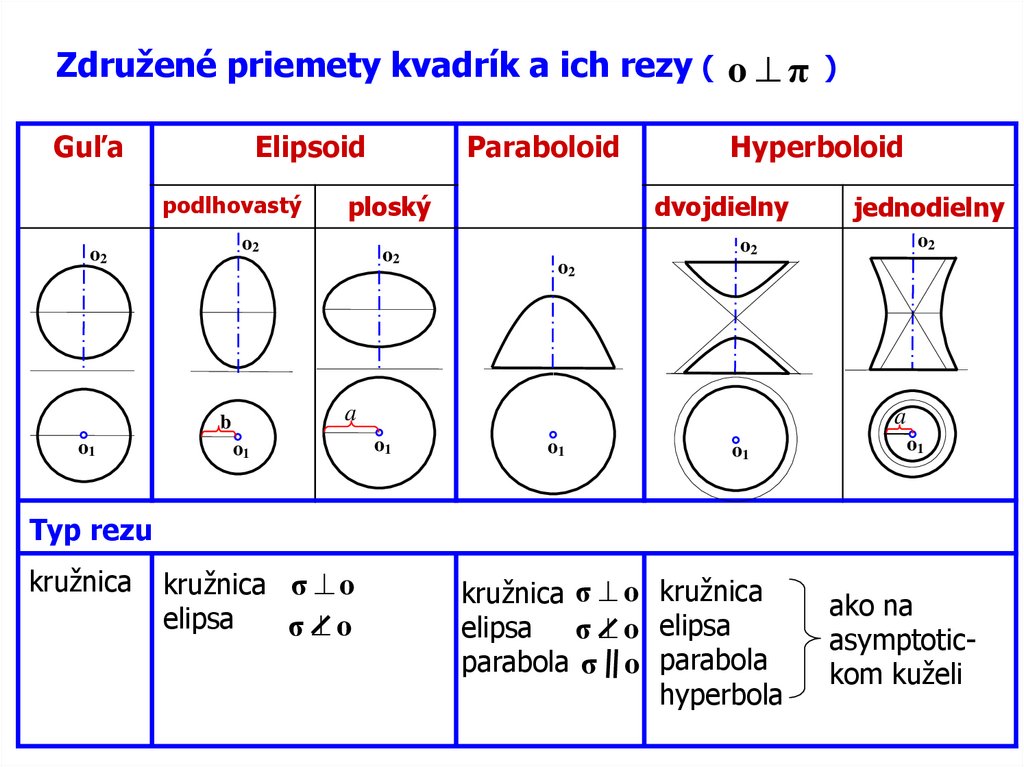
Združené priemety kvadrík a ich rezy ( o π )
Guľa
Elipsoid
podlhovastý
ploský
o2
o2
Paraboloid
o2
Hyperboloid
dvojdielny
jednodielny
o2
o2
o2
x1,2
a
b
o1
o1
a
o1
o1
o1
o1
Typ rezu
kružnica
kružnica σ o
elipsa
σ o
kružnica σ o kružnica
elipsa σ o elipsa
parabola σ o parabola
hyperbola
ako na
asymptotickom kuželi

11.

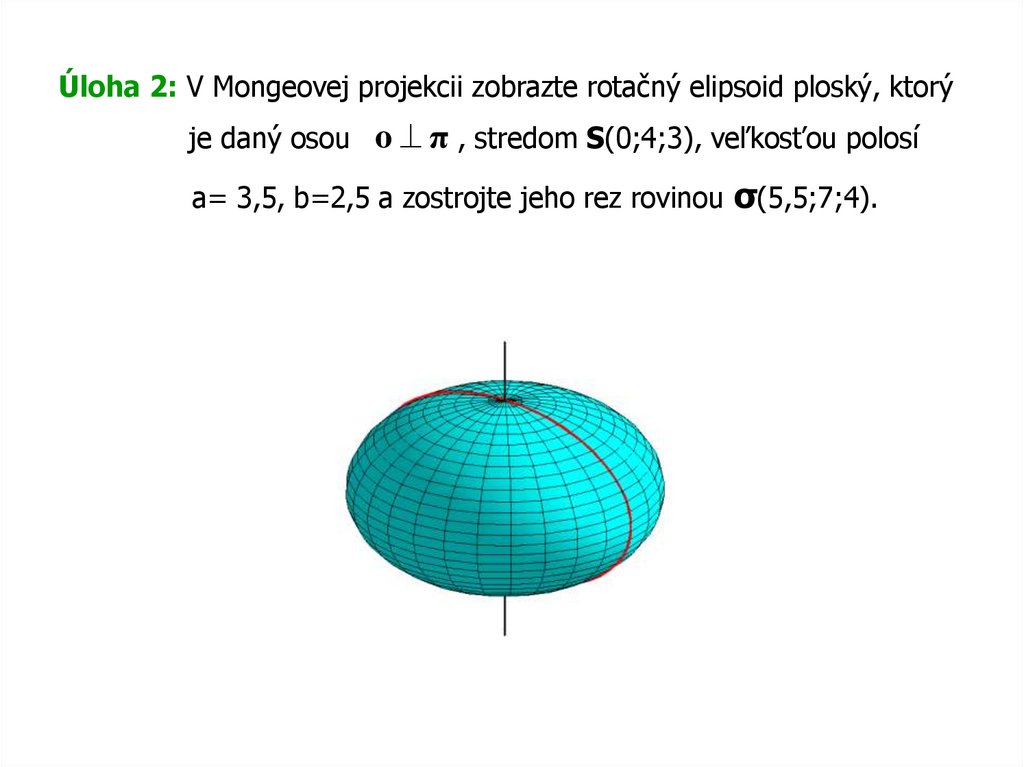
Úloha 2: V Mongeovej projekcii zobrazte rotačný elipsoid ploský, ktorý
je daný osou o π , stredom S(0;4;3), veľkosťou polosí
a= 3,5, b=2,5 a zostrojte jeho rez rovinou σ(5,5;7;4).

12.

2
h σ2
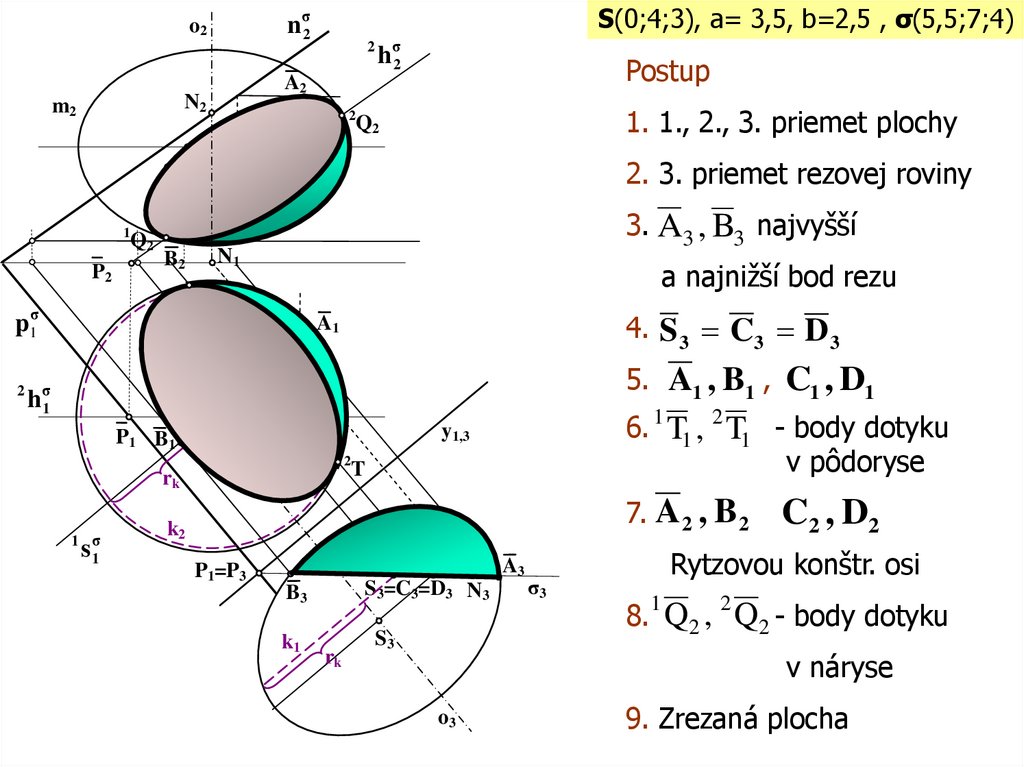
Postup
A2
N2
m2
S(0;4;3), a= 3,5, b=2,5 , σ(5,5;7;4)
n σ2
o2
1. 1., 2., 3. priemet plochy
2
Q2
S2
C2
D2
2. 3. priemet rezovej roviny
S2
3. A3 , B3 najvyšší
1
Q2
P2
N1
B2
a najnižší bod rezu
1
σ
1
T1
p
C1
h 1σ
o1=S1
2
4. S 3 C3 D 3
A1
5. A1 , B1 , C1 , D1
S1
6. 1 T1 , 2 T1 - body dotyku
v pôdoryse
y1,3
P1 B 1
2
rk
1 σ
1
s
o3
T1
D1
1
k2
7. A 2 , B 2
11
T33=22T33
P1=P3
S3=C3=D3 N3
B3
k1
rk
S3
A3
σ3
C2 , D2
Rytzovou konštr. osi
1
2
8. Q2 , Q2 - body dotyku
v náryse
o3
9. Zrezaná plocha

13.

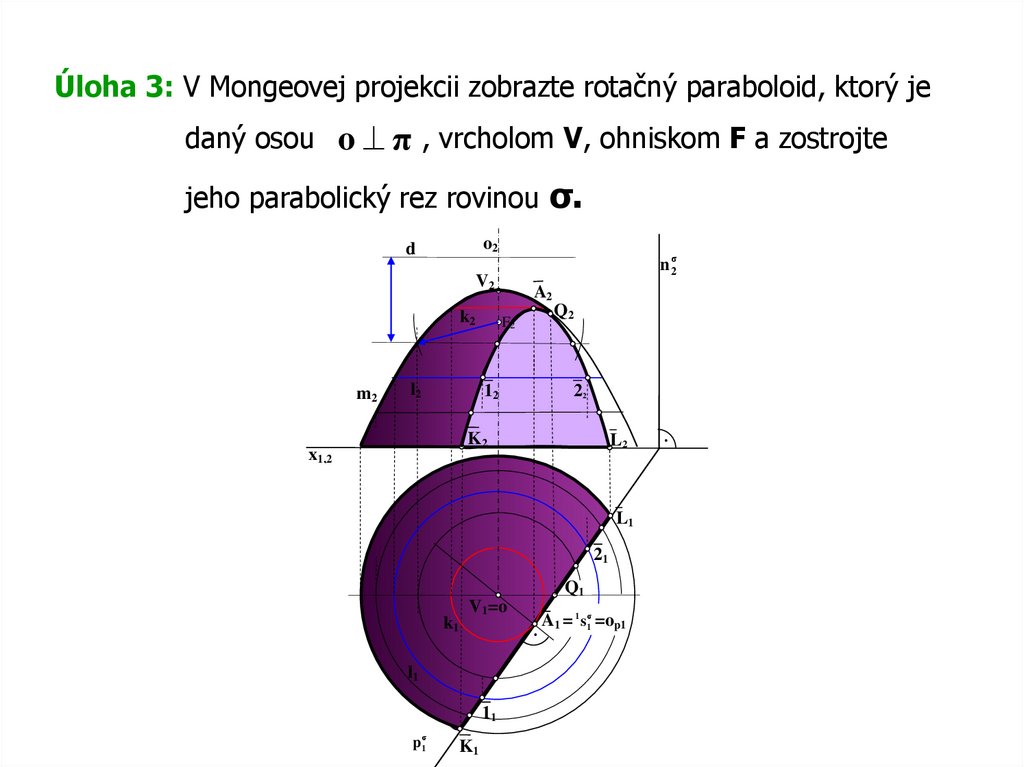
Úloha 3: V Mongeovej projekcii zobrazte rotačný paraboloid, ktorý je
daný osou o π , vrcholom V, ohniskom F a zostrojte
jeho parabolický rez rovinou σ.
o2
d
n σ2
V2
k2
m2
l2
o3
A2
F2
12
Q2
22
K2
x1,2
L2
L1
21
Q1
V1=o
k1 1
l1
11
p
o
σ
1
K1
A1 = 1 s1σ =op1

14.

o2
d
n σ2
V2
k2
o3
A2
F2
Q2
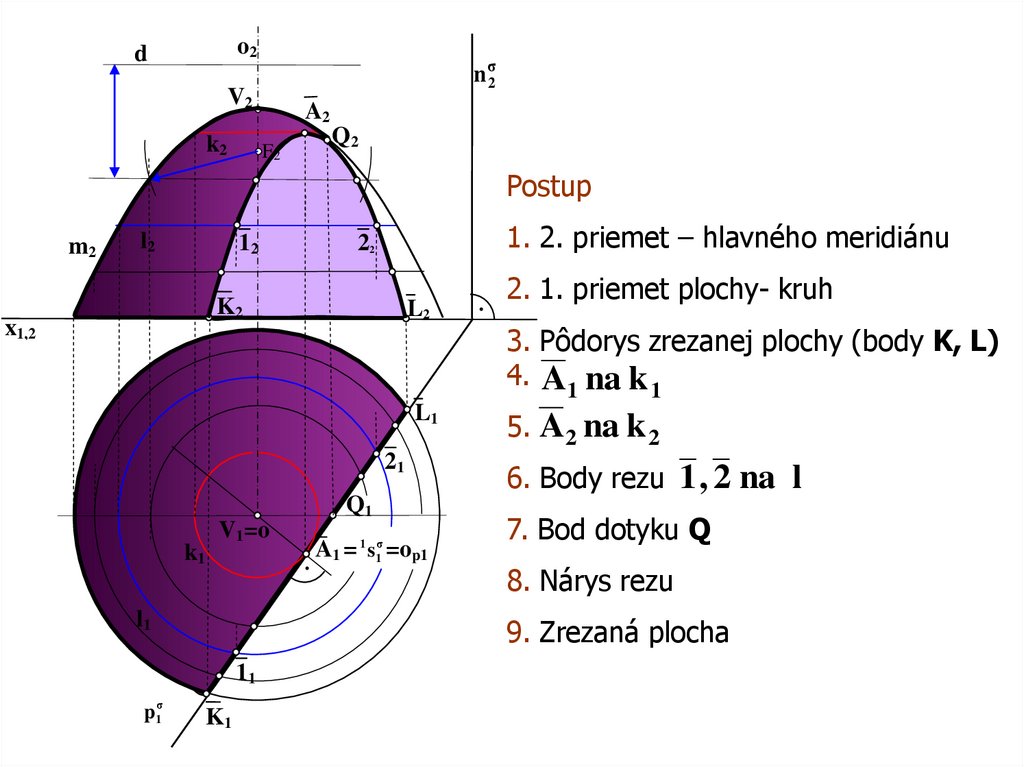
Postup
m2
l2
12
1. 2. priemet – hlavného meridiánu
22
K2
x1,2
L2
2. 1. priemet plochy- kruh
3. Pôdorys zrezanej plochy (body K, L)
4. A1 na k 1
L1
21
Q1
V1=o
k1 1
l1
6. Body rezu 1 , 2 na l
7. Bod dotyku Q
8. Nárys rezu
9. Zrezaná plocha
11
p1σ
o3
A1 = 1 s1σ =op1
5. A2 na k 2
K1

15.

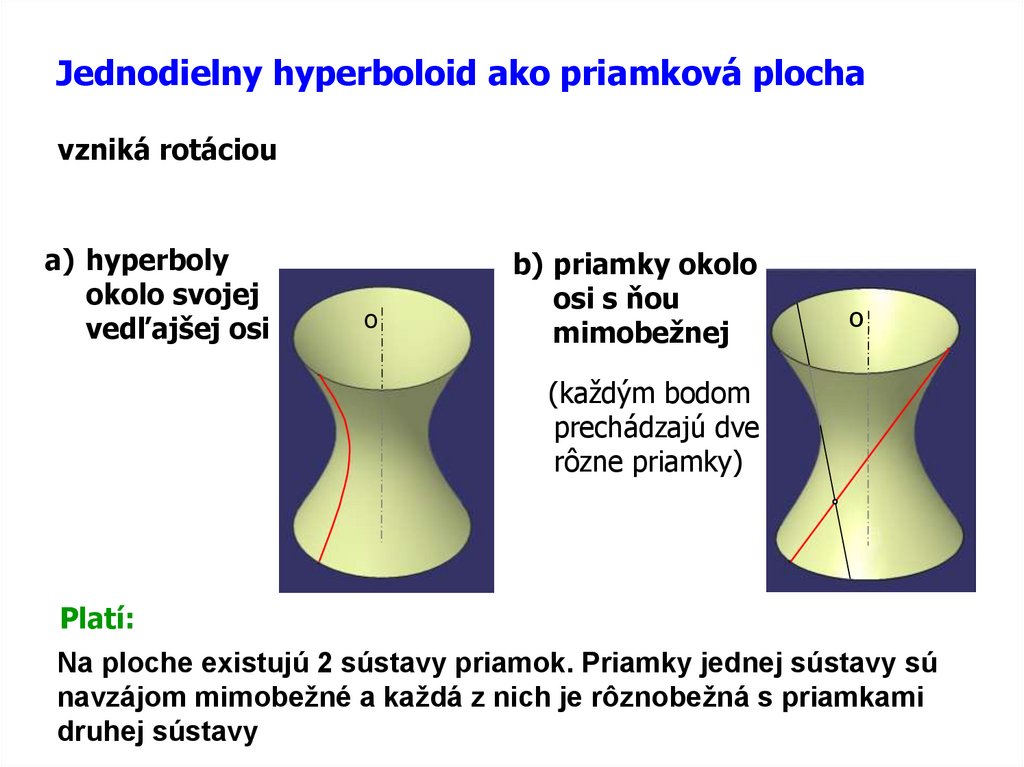
Jednodielny hyperboloid ako priamková plocha
vzniká rotáciou
a) hyperboly
okolo svojej
vedľajšej osi
o
b) priamky okolo
osi s ňou
mimobežnej
o
o
(každým bodom
prechádzajú dve
rôzne priamky)
Platí:
Na ploche existujú 2 sústavy priamok. Priamky jednej sústavy sú
navzájom mimobežné a každá z nich je rôznobežná s priamkami
druhej sústavy

16.

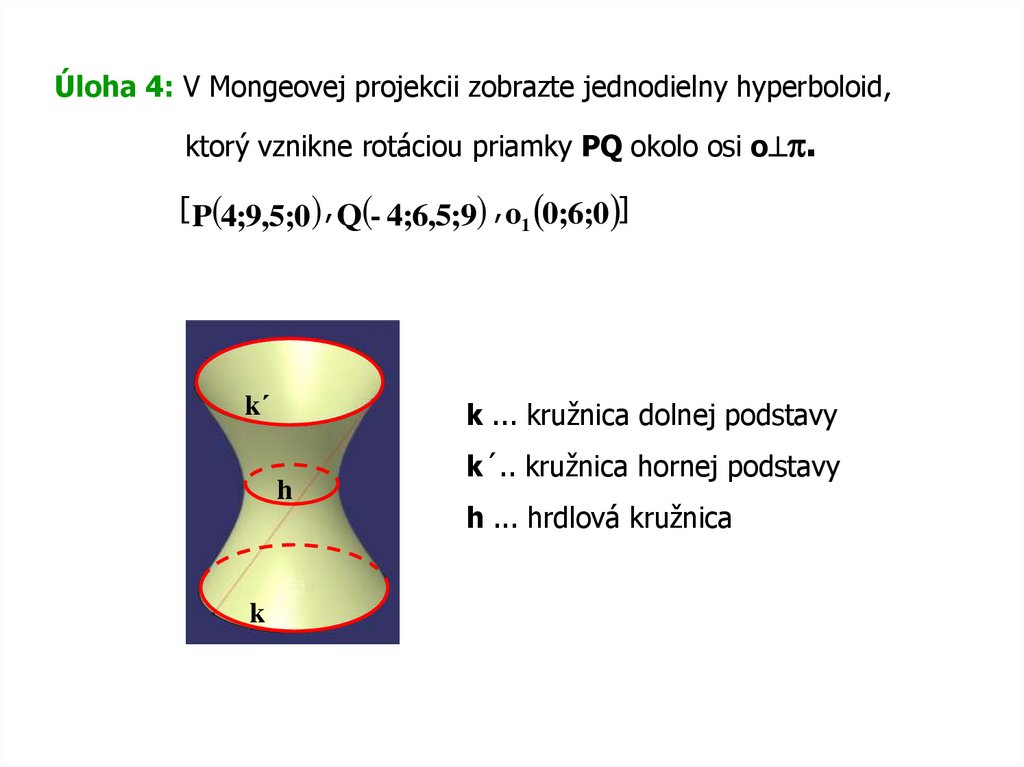
Úloha 4: V Mongeovej projekcii zobrazte jednodielny hyperboloid,
ktorý vznikne rotáciou priamky PQ okolo osi o .
[ P(4;9,5;0) , Q(- 4;6,5;9) , o1 0;6;0 ]
k´
k ... kružnica dolnej podstavy
h
k
k´.. kružnica hornej podstavy
h ... hrdlová kružnica

17.

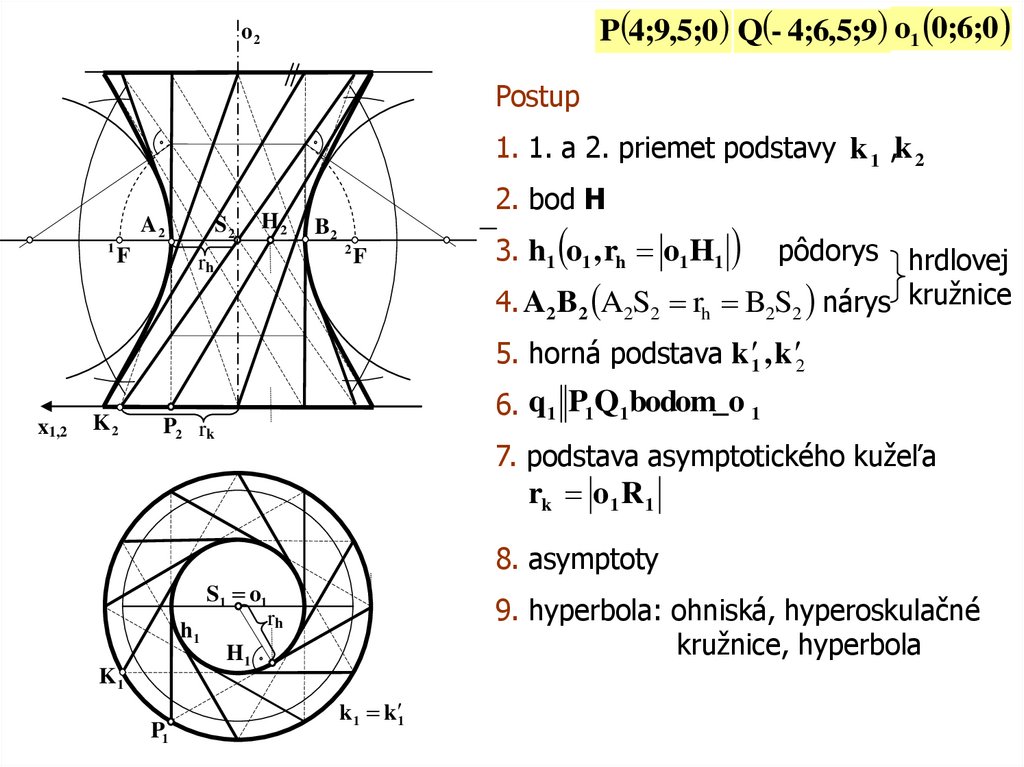
P(4;9,5;0) Q(- 4;6,5;9) o1 0;6;0
o2o2
k 2
Postup
Q2
1. 1. a 2. priemet podstavy k 1 ,k 2
A2
1
1
F
A2
F
rh
S2
rh
S 2 H H2
2
2. bod H
B2
B2
2
2
F
F
3. h1 o1 , rh o1H1
pôdorys
hrdlovej
4. A B A S r B S nárys kružnice
2
2
2 2
h
2 2
5. horná podstava k 1 , k 2
x1,2 K
x1,2
2
P
P2 2rk rrkk
rk
6. q1 P1Q1bodom_o 1
k2
7. podstava asymptotického kužeľa
rk o1 R 1
K1
S o
o
S1 11 o1 1
rh
r
h
h
1
R1 h1 rrkk
k H1
H
r
rkkk1
P
P1 1
q1
Q1
k k
k 1 1 k 1 1
8. asymptoty
9. hyperbola: ohniská, hyperoskulačné
kružnice, hyperbola

18.

Planetárium v Bochume, Nemecko

19.

McDonnell planetarium, Saint Louis, USA

20.

Chladiace veže Temelín, ČR

21.

22.

Fukui Prefectural Museum of Dinosaurus, Japonsko

23.

Budova spoločnosti Swiss Re, Londýn

24. Ďakujem za pozornosť

25.

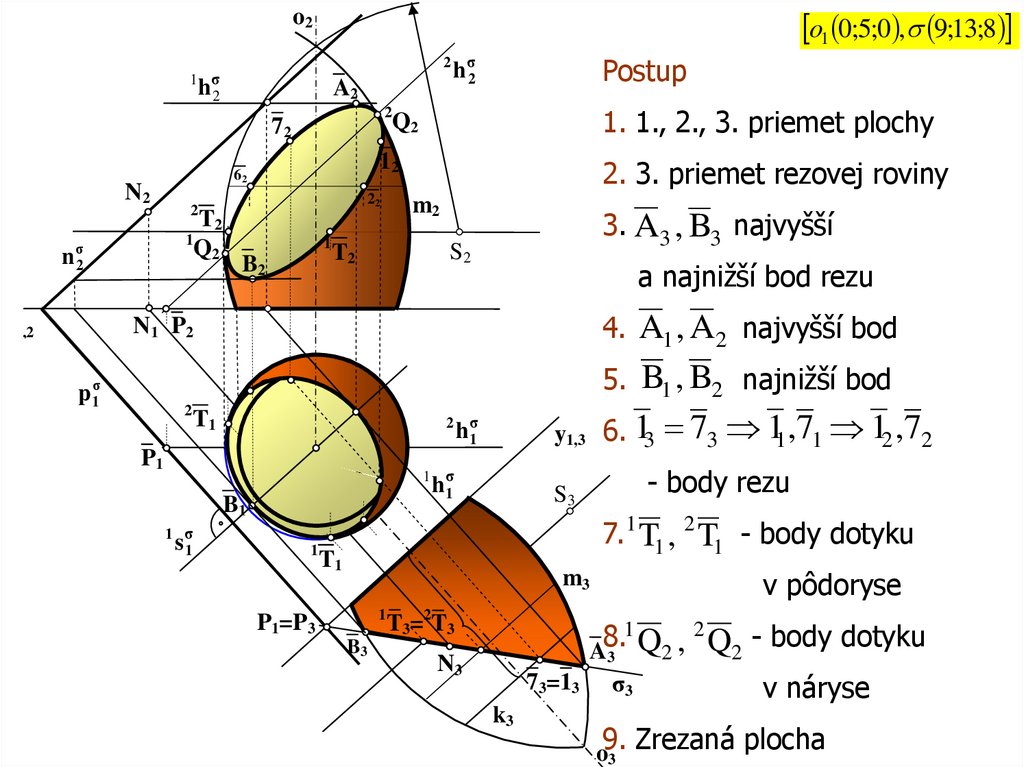
o1 0;5;0 , 9;13;8
o2
2
1 σ
h2
A2
2
72
22
2
T2
1
Q2
n σ2
o3
Q2
1. 1., 2., 3. priemet plochy
12
62
N2
Postup
h σ2
1
B2
2. 3. priemet rezovej roviny
m2
3. A3 , B3 najvyšší
S2
T2
a najnižší bod rezu
o3
4. A1 , A2 najvyšší bod
N1 P2
x1,2
p 1σ
2
o3
5. B1 , B2 najnižší bod
71
o1
T1
2
A1
P1
1 σ
h1
11
B1
1 σ
s1
k1
1
o3
y1,3 6. 13 73 11,71 12 ,72
h 1σ
- body rezu
S3
7. 1 T1 , 2 T1 - body dotyku
T1
v pôdoryse
m3
1
P1=P3
B3
T3=2T3
1
2
8.
Q
,
Q2 - body dotyku
A
2
3
N3
73=13
k3
σ3
v náryse
Zrezaná plocha
o9.
3