Лекция 1 ТПР

1.

Филиал ФГБОУ ВО
«Национальный исследовательский университет «МЭИ» в г. Смоленске
Теория принятия решений
Доцент кафедры ВТ
кандидат технических наук, доцент
И.А. Денисова
Смоленск
Смоленск
– 2024
2011

2.

ПОРЯДОК ИЗУЧЕНИЯ ДИСЦИПЛИНЫ
На изучение дисциплины отводится: 18 часов лекций + 16
На изучение дисциплины отводится: 18 часов лекций + 16
часов практических занятий + 65 часов самостоятельной
часов практических занятий + 65 часов самостоятельной
работы.
работы.
Завершается изучение дисциплины зачетом с оценкой.
Завершается изучение дисциплины зачетом с оценкой.

3.

Лекция № 1
Основы теории принятия решений

4.

УЧЕБНЫЕ ВОПРОСЫ
1. Основы теории принятия решений.
2. Исследование операций. Математические модели
операций.

5.

1 вопрос
Основы теории принятия решений

6.

Процессы принятия решения лежат в основе любой
целенаправленной деятельности.
Оптимальные
(эффективные)
решения
позволяют
достигать цели при минимальных затратах ресурсов.
Основы теории принятия решения были разработаны
американскими учеными Джоном фон Нейманом и Отто
Моргенштерном в 40-х годах двадцатого века.
Как самостоятельная дисциплина теория принятия
решения (ТПР) сформировалась в начале 60-х годов, тогда
же была сформулирована основная цель этой теории рационализировать процесс принятия решения.
66

7.

Принятие решения в профессиональном отношении
представляет
собой
особый
вид
человеческой
деятельности, который состоит в обоснованном выборе
наилучшего в некотором смысле варианта или нескольких
предпочтительных вариантов из имеющихся возможных.
1.
2.
3.
4.
5.
6.
7.
8.
Общая схема процесса принятия решений
Выявление, анализ, диагностика проблемы.
Формирование целей и задач решения проблемы с учетом ограничений.
Анализ способов решения проблемы и адекватных им управленческих
решений.
Моделирование вариантов сценариев, оценка результатов и последствий
реализации разных вариантов.
Выбор предпочтительного варианта, обоснование выбора.
Принятие управленческого решения.
Доведение принятого решения до исполнения.
77
Управление реализацией решения.

8.

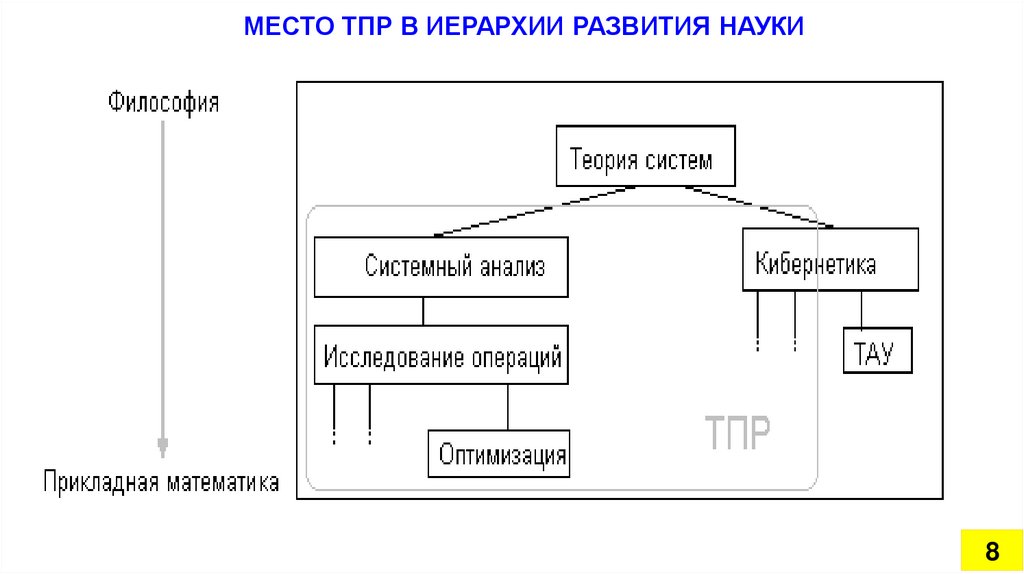
МЕСТО ТПР В ИЕРАРХИИ РАЗВИТИЯ НАУКИ
8

9.

«Кибернетика – это наука об
оптимальном управлении
сложными динамическими
системами»
А́ксель Ива́нович Берг
1893 - 1979
советский учёный
радиотехник, адмирал,
заместитель министра
обороны СССР
«Кибернетика – это наука о
системах, воспринимающих,
хранящих, перерабатывающих
и использующих информацию»
Андре́й Никола́евич
Колмого́ров
1903 - 1987
советский математик,
один из крупнейших
математиков ХХ века
9

10.

Илья́ Рома́нович
Приго́жин
1917 - 2000
советский и российский
учёный в области общей
механики и прикладной
математики, академик
Академии наук СССР
Системный анализ – это
совокупность методов,
основанных на использовании
ЭВМ и ориентированных на
исследование сложных систем –
технических, экономических,
экологических и т. д.
Центральной проблемой
системного анализа является
проблема принятия решения.
10

11.

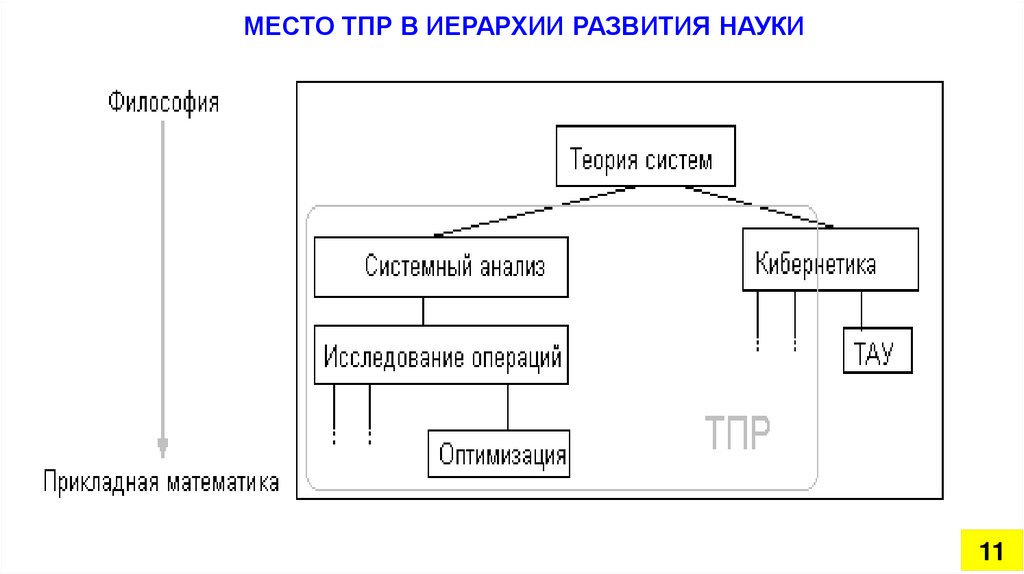
МЕСТО ТПР В ИЕРАРХИИ РАЗВИТИЯ НАУКИ
11

12.

ОСНОВОПОЛАГАЮЩИЙ ПРИНЦИП ТПР
сформулировали
Моргенштерн:
американские
ученые
Нейман
и
Лицо, принимающее решение, должно всегда
выбирать альтернативу с максимально ожидаемой
полезностью, результатом.
12

13.

ФАКТОРЫ, ВЛИЮЯЩИЕ НА ПРИНЯТИЕ РЕШЕНИЯ
• неопределенность природы (факторы, людям неизвестные или
от них не зависящие);
• неопределенность человека, который может вести себя
непоследовательно, противоречиво, допускать ошибки, зависеть от
других лиц (партнеров, противников и т. д.), чьи действия он не может
полностью учесть или предвидеть;
• неопределенность целей.
13

14.

2 вопрос
Исследование операций.
Математические модели операций.

15.

сформулировали
Моргенштерн:
американские
ученые
Нейман
и
Исследование операций - основной научный
инструмент при принятии оптимальных решений в
самых
разнообразных
областях
человеческой
деятельности.
Цель исследования операций - предварительное
количественное обоснование оптимальных решений.
15

16.

Под исследованием операций понимают применение
математических, количественных методов для
обоснования решений во всех областях
целенаправленной человеческой деятельности.
Исследование операций начинается тогда, когда для
обоснования решений применяется тот или другой
математический аппарат.
Исследование операций - это своеобразное
математическое «примеривание» будущих решений,
позволяющее экономить время, силы и материальные
средства, избегать серьезных ошибок, на которых уже
нельзя «учиться» (слишком дорого это обходится).
16

17.

17

18.

Оптимизация - целенаправленная деятельность,
заключающаяся в получении наилучших результатов при
соответствующих условиях.
Формулировка математической задачи оптимизации минимизировать (максимизировать) целевую функцию с учетом
ограничений на управляемые переменные.
18

19.

При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации.
2. Наличие ресурсов оптимизации.
3. Возможность количественной оценки оптимизируемой
величины.
4. Учет ограничений.
19

20.

Критерием оптимальности (он же целевая функция)
называется количественная оценка оптимизируемого качества
объекта.
Критерий оптимальности может быть представлен как
функция переменных:
f (x1, x2,...,xn,)→ opt (min/max)
Ограничения задачи задаются в виде системы уравнений
либо неравенств.
20

21.

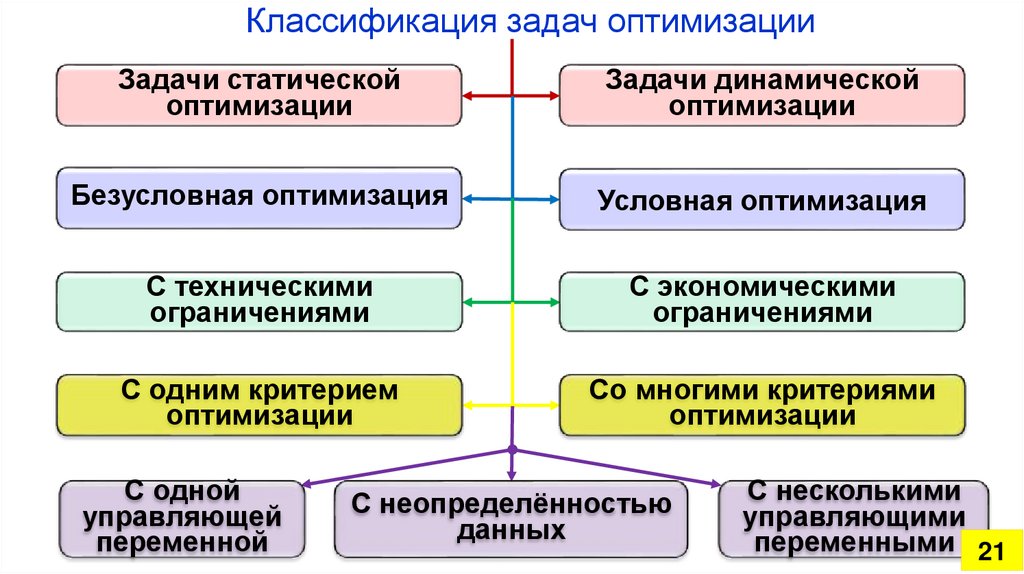
Классификация задач оптимизации
Задачи статической
оптимизации
Задачи динамической
оптимизации
Безусловная оптимизация
Условная оптимизация
С техническими
ограничениями
С экономическими
ограничениями
С одним критерием
оптимизации
Со многими критериями
оптимизации
С одной
управляющей
переменной
С неопределённостью
данных
С несколькими
управляющими
переменными 21

22.

Последовательность решения задачи оптимизации
Составление математической модели
объекта оптимизации
Выбор критерия оптимальности и
составление целевой функции
Установление возможных ограничений
Выбор метода оптимизации
22

23.

Методы решения оптимизационных задачи
Математическое программирование:
линейное программирование;
целочисленное программирование;
нелинейное программирование;
динамическое программирование;
теория игр;
методы исследования функций классического анализа;
метод множителей Лагранжа;
вариационное исчисление;
принцип максимума;
геометрическое программирование и другие.
23

24.

Методы линейного программирования применяют для решения
оптимальных задач с линейными функциями цели. На независимые
переменные могут быть наложены ограничения в виде равенств или
неравенств.
В общем случае модель задачи ЛП имеет вид
L C1 x1 C2 x2 ... C j x j ... Cn xn opt
при ограничениях:
a11 x1 a12 x2 ... a1n xn b1
a
b2
21 x1 a 22 x2 ... a 2 n xn
...
ai1 x1 ai 2 x2 ... ai n xn bi
...
am1 x1 am 2 x2 ... amn xn bm
24

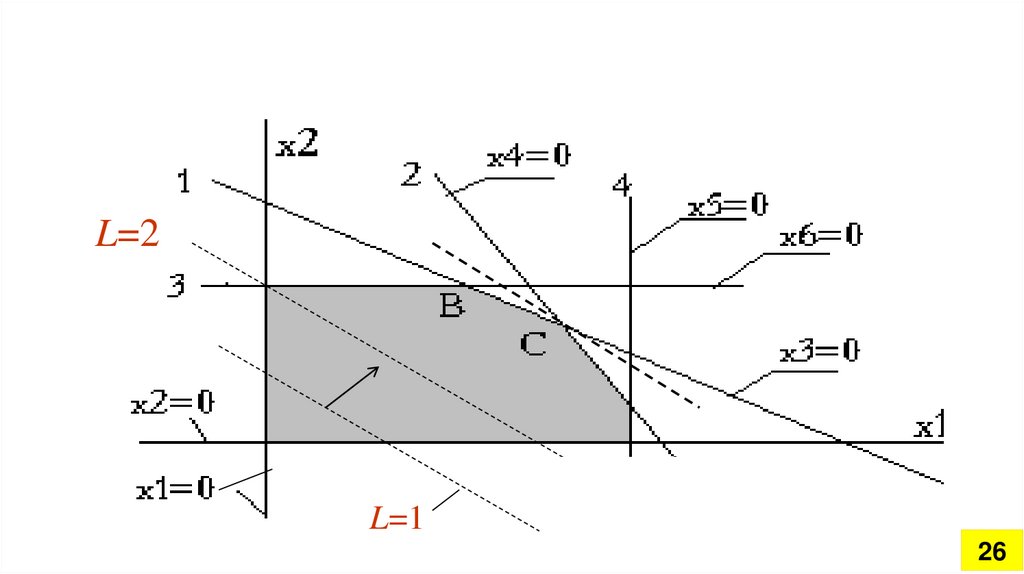
25.

Пример задачи ЛП
L=7x1+5x2→max
2x1+3x2 19 (1)
2x1+x2 13 (2)
3x2 12
(3)
3x1 17
(4)
x1 0
(5)
x2 0
(6)
25

26.

L=2
L=1
26

27.

Задачи целочисленнго пограмрмирования отличаются тем,
что на переменные накладывается требование целочисленности.
Характерные источники целочисленности (дискретности):
неделимость объектов, представляемых переменными
(например, x – число ракет или единиц техники);
вариантность типа “да-нет” (например, включать или нет
данное подразделение в план операции);
заданность возможных значений нормативными
документами (например, сечения проводов, диаметров труб,
грузоподъемность моста и т.п.);
комбинаторность (например, размещение объектов, порядок
обхода объектов, упорядочение).
27

28.

Пример задачи ЦЛП
Требуется закупить для столовой некоторый продукт в
количестве 107 кг. Данный продукт продается только в
расфасованном виде: 1) мешок весом 35 кг стоит 1400 руб.; 2) мешок
весом 24 кг стоит 1200 руб. Необходимо определить вариант закупки
с минимальными затратами.
Модель задачи:
L=1400x1+1200x2 min;
35x1+24x2 107;
x1, x2 0, int (целые).
28

29.

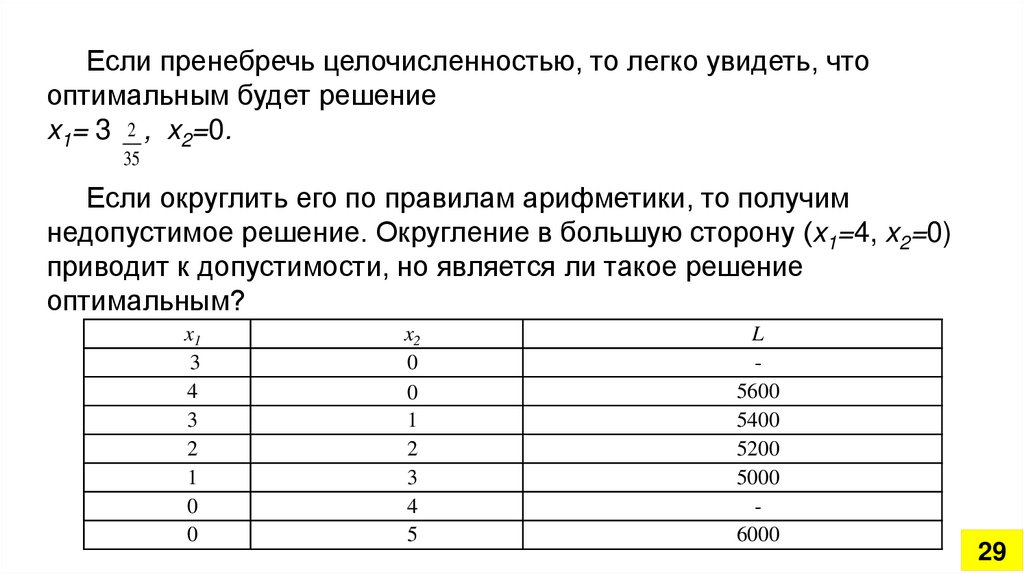
Если пренебречь целочисленностью, то легко увидеть, что
оптимальным будет решение
x1= 3 2 , x2=0.
35
Если округлить его по правилам арифметики, то получим
недопустимое решение. Округление в большую сторону (x1=4, x2=0)
приводит к допустимости, но является ли такое решение
оптимальным?
x1
3
4
3
2
1
0
0
x2
0
0
1
2
3
4
5
L
5600
5400
5200
5000
6000
29

30.

Методы нелинейного программирования применяют для
решения оптимальных задач с нелинейными функциями. На
независимые переменные могут быть наложены ограничения в виде
равенств или неравенств.
30

31.

Концепция метода динамического программирования
проистекает из следующего свойства оптимального решения. Пусть
оптимальный путь из точки A в точку E проходит через точки B, С и D.
Тогда любая часть этого пути является оптимальным путем.
31

32.

Фундаментальной основой метода динамического
программирования является сформулированный Беллманом
принцип оптимальности, согласно которому оптимальное
управление определяется конечной целью управления и состоянием
системы в рассматриваемый момент, независимо от того, каким
образом она пришла в это состояние. Иначе говоря, при
фиксированном состоянии системы последующее оптимальное
решение не зависит от ее предыстории.
Принцип оптимальности Беллмана. Оптимальное
поведение обладает тем свойством, что каковы бы ни были
первоначальное состояние и решение в начальный момент,
последующие решения должны составлять оптимальное
поведение относительно состояния, получающегося в
результате первого решения.
32

33.

ЗАДАНИЕ НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
1. Составить математическую модель задачи ЛП
Для изготовления двух видов изделий А и Б используют три вида сырья.
На производство единицы изделия А требуется затратить сырья 1-го вида 13
кг, сырья 2-го вида 32 кг, сырья 3-го вида 58 кг. На производство единицы
изделия Б требуется затратить сырья 1-го вида 24 кг, сырья 2-го вида 32 кг,
сырья 3-го вида 29 кг. Производство обеспечено сырьем 1-го вида в
количестве 312 кг, сырья 2-го вида 480 кг, сырья 3-го вида 696 кг. Прибыль от
реализации единицы готового изделия А составляет 4 усл. ед., от
реализации единицы готового изделия Б – 3 усл. ед.
Требуется составить план производства изделий А и Б, обеспечивающий
максимальную прибыль от их реализации, если заранее планируется
изготовить не менее 10 единиц изделий А и Б (суммарно).
2. Решить задачу ЛП.
33