Paradoks-Vorony-Gempelya

1.

Парадокс «Вороны
Гемпеля»
Когда зеленое яблоко доказывает, что все вороны черные.

2.

Введение: Вопрос на засыпку
Представьте, что вы ученый и хотите доказать гипотезу: «Все вороны
черные».
1
Индуктивное подтверждение
Каждая найденная черная ворона подтверждает теорию.
2
Парадокс
Что, если зеленое яблоко или красный гидрант тоже доказывают
это?

3.

Суть парадокса: Логический трюк
Карл Густав Гемпель использовал простые законы формальной логики.
Исходное утверждение
«Все вороны черные» (Если X — ворона, то X — черный).
Равносильное утверждение
По законам логики (контрапозиция): «Если X — НЕ черный,
то X — НЕ ворона».

4.

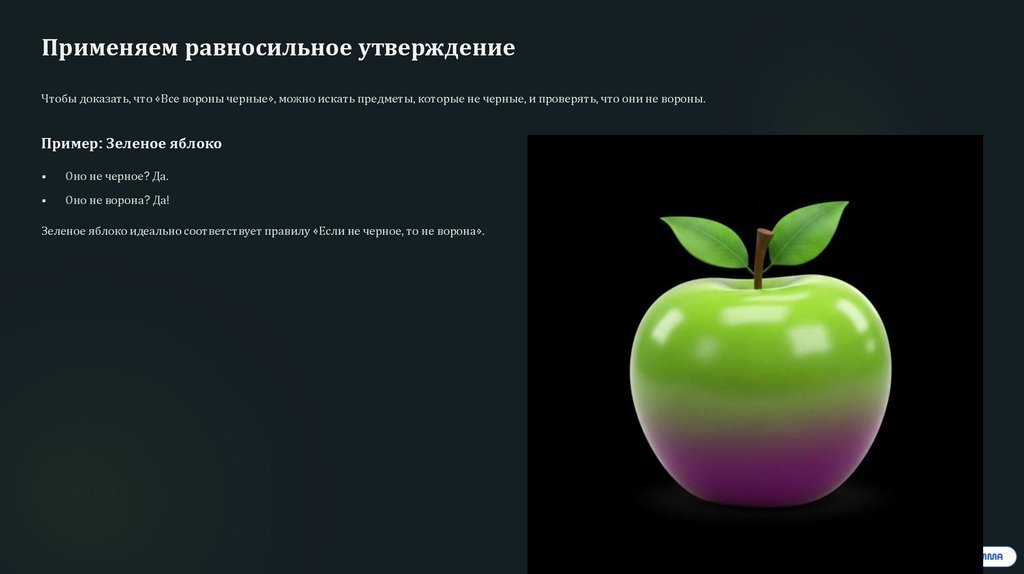
Применяем равносильное утверждение
Чтобы доказать, что «Все вороны черные», можно искать предметы, которые не черные, и проверять, что они не вороны.
Пример: Зеленое яблоко
Оно не черное? Да.
Оно не ворона? Да!
Зеленое яблоко идеально соответствует правилу «Если не черное, то не ворона».

5.

Почему это парадоксально?
Разрыв между интуицией и формальной логикой.
Формальная логика
Яблоко — подтверждающий пример. Все чисто.
Наша интуиция
Это нелепо. Как яблоко может говорить о воронах?

6.

Значение и выводы
Парадокс Гемпеля — это не про биологию, а про философию науки и логику.
01
02
03
Сомнение в индукции
Разрыв со здравым смыслом
Тренировка для ума
Не все подтверждения одинаково
Учит критически относиться к
полезны. Важны рискованные,
Парадокс заставляет уточнять, что мы
информативные проверки.
понимаем под «подтверждением
теории».
очевидным выводам и формулировкам.

7.

Заключение
Парадокс «Вороны Гемпеля» — мощный инструмент для осмысления научного метода.
Логика vs Интуиция
Чистая логика может противоречить
здравому смыслу.
Основы науки
Не про орнитологию, а про то, как
мы получаем знание.
Без решения
Парадокс не имеет одного решения, но
стимулирует мышление.
В следующий раз, увидев зеленое яблоко, вспомните о черных воронах!