Л5 _ТЙКС(20.11.25)

1.

1

2.

КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
імені ТАРАСА ШЕВЧЕНКА
Кафедра інформаційних систем та технологій
ТЕОРІЯ ЙМОВІРНОСТЕЙ та КОМП'ЮТЕРНА СТАТИСТИКА
Викладачі: Володимир ДРУЖИНІН; Ганна ТЕРЕЩУК
2025

3.

ЛЕКЦІЯ № 5: «Комп'ютерна статистика. Закон великих чисел. Необхідна та
достатня умова для закону великих чисел. Посилений закон великих чисел.
Центральна гранична теорема. Емпіричні розподіли і форми їх представлення»
Навчальні питання:
1. Розподіли, пов'язані з нормальним (*** матеріал лекції № 4 - останнє
питання).
2. Закон великих чисел.
3. Емпіричні розподіли і форми їх представлення.
2

4.

1. Розподіли, пов'язані з нормальним
*** Часто використовуються, особливо в математичній статистиці, деякі
розподіли неперервних випадкових величин, пов’язані з нормальним.
Для їх розгляду введемо поняття стандартного нормального розподілу.
Означення. Стандартною нормально розподіленою величиною (або просто
стандартною) називається випадкова величина Y, що розподілена за нормальним
законом з числовими характеристиками
M(Y)=0; D(Y)=1.
3

5.

!!! Будь-яку випадкову величину Х, розподілену за нормальним законом з
довільними числовими характеристиками
можна звести до стандартної лінійним перетворенням
(3.38)
Щільність розподілу ймовірностей для стандартної нормально розподіленої
величини записується у вигляді
(3.39)
4

6.

*** Приведення до стандартного нормального розподілу можна виконати з
використанням вбудованої функції
MS Excel НОРМАЛИЗАЦИЯ (х, а, σ ),
параметри якої зрозумілі з позначень.
Якщо Y1, Y2, ..., Yn – незалежні випадкові величини зі стандартним
нормальним розподілом, то величина
(3.40)
має розподіл
*** (читається «хі-квадрат») з n ступенями свободи.
5

7.

Зрозуміло, що величина «хі-квадрат» приймає тільки додатні значення і
залежить тільки від числа доданків у сумі (числа ступенів свободи).
Доведено, що аналітичний вираз для щільності розподілу має вид:
(3.41)
6

8.

7

9.

При
n > 30
розподіл наближається до нормального з параметрами
8

10.

Ще один розподіл, пов’язаний з нормальним, досліджений англійським
математиком Госсетом (W.S. Gosset), який писав статті під псевдонімом Student
(саме тому розподіл одержав назву розподілу Стьюдента).
Нехай Y – випадкова величина зі стандартним нормальним розподілом, а Z
незалежна від Y випадкова величина, що має розподіл
з n ступенями свободи.
Тоді випадкова величина
(3.42)
має розподіл Стьюдента (t - розподіл) з n ступенями свободи.
9

11.

Щільність такого розподілу виражається формулою
(3.43)
!!! Розподіл Стьюдента є симетричним і одномодальним, внаслідок чого
легко визначити характеристики положення випадкової величини Х:
M(X) = Мо = Ме = 0
*** Доведено, що
D(X) = n/(n–2)
для
n>2
*** Для інтегральної функції розподілу Стьюдента також складені таблиці. При
великих n розподіл наближається до стандартного нормального розподілу.

12.

F - розподіл (розподіл Снедекора, а в деяких джерелах – Фішера-Снедекора)
має місце для випадкової величини
(3.44)
де Y i Z – дві незалежні випадкові величини, які мають розподіл хі - квадрат з
n i m ступенями свободи відповідно.
!!! Як видно, на відміну від розглянутих раніше розподілів, F – розподіл
визначається парою ступенів свободи (n, m).
Щільність F- розподілу задається формулою
(3.45)
11

13.

Числові характеристики
обчислюються за формулами:
випадкової
величини,
яка
має
F-розподіл,
Для обчислення ймовірностей можна використати стандартну функцію
MS Excel FРАСП(х, n, m), при цьому
12

14.

Z-розподіл (або розподіл дисперсійного відношення Фішера).
Якщо Y – випадкова величина, що має F - розподіл з (n, m) ступенями
свободи, то випадкова величина
(3.46)
має Z-розподіл з (n, m) ступенями свободи, щільність розподілу і числові
характеристики якого виражаються формулами
(3.47)
13

15.

2. Закон великих чисел
*** Узагальнену назву «закон великих чисел» отримала система теорем, яка
є перехідною до розділів математичної статистики і яка вивчає властивості
різних характеристик, отриманих за результатами великої кількості дослідів.
!!! Можна стверджувати, що закон великих чисел обґрунтовує
статистичний підхід до теорії ймовірностей і одночасно є теоретичним
фундаментом математичної статистики.
14

16.

*** Розглянемо неперервну випадкову величину Х, задану щільністю
розподілу f(x), з обмеженими математичним очікуванням
Виберемо довільну величину
ε>0
і будемо шукати ймовірність того, що відхилення випадкової величини від
центру розподілу перевищить задане число ε:
15

17.

Таким чином, якщо невід’ємний підінтегральний вираз помножити на
останній дріб, величина інтегралу від цього не зменшиться:
Оскільки підінтегральна функція невід’ємна,
інтегрування не зменшить величини інтегралу
збільшення
інтервалу
16

18.

Таким чином, одержана нерівність
(4.1)
Ця нерівність відома як нерівність Чебишева.
!!! Вона слушна як для дискретних, так і для неперервних випадкових
величин для будь-якого закону розподілу.
*** Зауважимо, що оцінка, отримана за нерівністю Чебишева, в ряді випадків
є дуже наближеною.
Так, для нормального закону відоме співвідношення
а з нерівності Чебишева витікає оцінка
17

19.

!!! На основі нерівності Чебишева можна ввести поняття «збіжності за
ймовірністю».
Розглянемо послідовність випадкових величин
Х1, Х2, ..., Хn,
для якої
*** Якщо до членів послідовності застосувати нерівність Чебишева,
отримаємо
18

20.

*** Враховуючи, що ймовірність є невід’ємною, нерівність стає рівнянням
а після переходу до протилежної події отримаємо
Означення. Послідовність випадкових величин Хn збігається за ймовірністю
до сталого числа а, якщо для довільного числа
ε>0
ймовірність нерівності
19

21.

*** Позначається сказане вище наступним чином
(4.2)
!!! Слід відмітити, що збіжність за ймовірністю є дещо «м’якішою» умовою,
ніж умова збіжності в математичному аналізі; замість жорсткої умови виконання
нерівності починаючи з деякого члену послідовності N, тут вимагається
ймовірність виконання нерівності (рівність ймовірності одиниці не означає, що
подія є достовірною, тобто відбудеться обов’язково).
20

22.

*** Збіжність за ймовірністю використовується для доведення кількох теорем.
Розглянемо послідовність випадкових величин Х1, Х2, ..., Хn, для кожної з
яких визначені математичні очікування і дисперсії.
Для перших n членів послідовності будемо обчислювати середнє
арифметичне
і його числові характеристики:
21

23.

*** Позначимо
і при збільшенні числа доданків, за якими обчислюється середнє
арифметичне, дисперсія результату прямує до нуля.
Використовуючи нерівність Чебишева, маємо
22

24.

Таким чином отримується теорема Чебишева: якщо у послідовності
попарно незалежних випадкових величин всі дисперсії обмежені, то
послідовність середніх арифметичних збігається за ймовірністю до
математичного очікування цієї послідовності.
*** Як окремий випадок теореми Чебишева можна розглядати теорему Бернуллі.
Дійсно, в схемі повторних випробувань Бернуллі число появ події можна розглядати
як суму допоміжних величин, розподілених за законом розподілу Бернуллі.
В цьому випадку відносну частоту появи подій можна розглядати як середню
арифметичну із значень допоміжних величин, внаслідок чого маємо
23

25.

!!! В останньому співвідношенні використана властивість розподілу Бернуллі:
М(Yi) = р.
!!! Теорема Бернуллі: відносна частота події при збільшенні числа дослідів
збігається за ймовірністю до ймовірності появи події при одному випробуванні.
24

26.

3. Емпіричні розподіли і форми їх представлення
*** В математичній статистиці розглядаються результати обробки вже
виконаних дослідів на деякій множині елементів.
!!! При цьому можуть розглядатися як вся множина елементів, так і певна її
частина.
Генеральною
сукупністю
досліджуваної множини.
називається
сукупність
усіх
значень
Вибірковою сукупністю (вибіркою) називається сукупність випадково
відібраних значень досліджуваної множини.
*** Слід зауважити, що метою досліджень завжди є властивості усієї множини,
тобто властивості генеральної сукупності, але з технічних чи економічних причин
досить часто доводиться обмежитись дослідженням вибірки.
25

27.

!!! Сутність вибіркового методу полягає в тому, що характеристики
вибіркової сукупності приймаються в якості наближених значень відповідних
характеристик генеральної сукупності.
!!! Задача математичної статистики - кількісна оцінка значень похибок, які
виникають при використанні наближених значень.
*** Існує ціла теорія експерименту, в якій аналізуються методи організації
вибіркової сукупності, які дозволяють суттєво зменшити похибки від заміни
генеральної сукупності вибіркою.
26

28.

!!! Вибірка повинна бути репрезентативною, тобто вірно представляти
пропорції генеральної сукупності.
*** Вибірка завжди буде репрезентативною, якщо її формувати випадково,
тобто так, щоб всі об’єкти мали однакову ймовірність попасти до вибірки.
Комп ютерна статистика базується на апараті теорії ймовірностей, тому для
багатьох характеристик використовуються статистичні аналоги понять з теорії
ймовірностей.
27

29.

СТАТИСТИЧНІ АНАЛОГИ
Статистичним аналогом ймовірності є відносна частота появи події з
заданою властивістю
W(A)=ni /n,
де ni – кількість елементів множини, що мають задану властивість, n –
загальний об’єм сукупності.
Зрозуміло, що
28

30.

Статистичним аналогом ряду розподілу є статистичний (або емпіричний)
ряд – таблиця, в якій наведені упорядковані за величиною значення
досліджуваної величини і відповідні відносні частоти.
Приклад. За результатами сесії деканати складають такі таблиці (хі – оцінка
на екзамені)
29

31.

!!! (УВАГА) На відміну від теорії ймовірностей, де ряд розподілу
складається тільки для дискретних випадкових величин, в статистиці ряд
складається і для неперервних вимірюваних величин, але при цьому результати
вимірювань (вони завжди дискретні!) групують на деяких інтервалах.
*** Якщо, наприклад, вимірюється зріст студентів групи, то статистичний
ряд може мати такий вид (уі – зріст студента )
30

32.

!!! Кількість інтервалів групування і їх довжину вибирають таким чином,
щоб результати були виразні і наочні.
***Так, інтервал повинен бути сталим, щоб відображати властивості
сукупності, а не довжини інтервалу; довжина інтервалу повинна бути значно
більшою за похибки вимірювання.
Для обчислення довжини інтервалу великих вибірок використовується
формула Стеджерса
(4.3)
де hх – довжина інтервалу групування, Хmax, Х min – максимальне і мінімальне
значення елементів вибірки, n – об’єм вибіркової сукупності.
*** Початок першого інтервалу групування повинен бути не більшим мінімального
значення відповідної величини, кінець останнього – не меншим за максимальне
31
значення величини.

33.

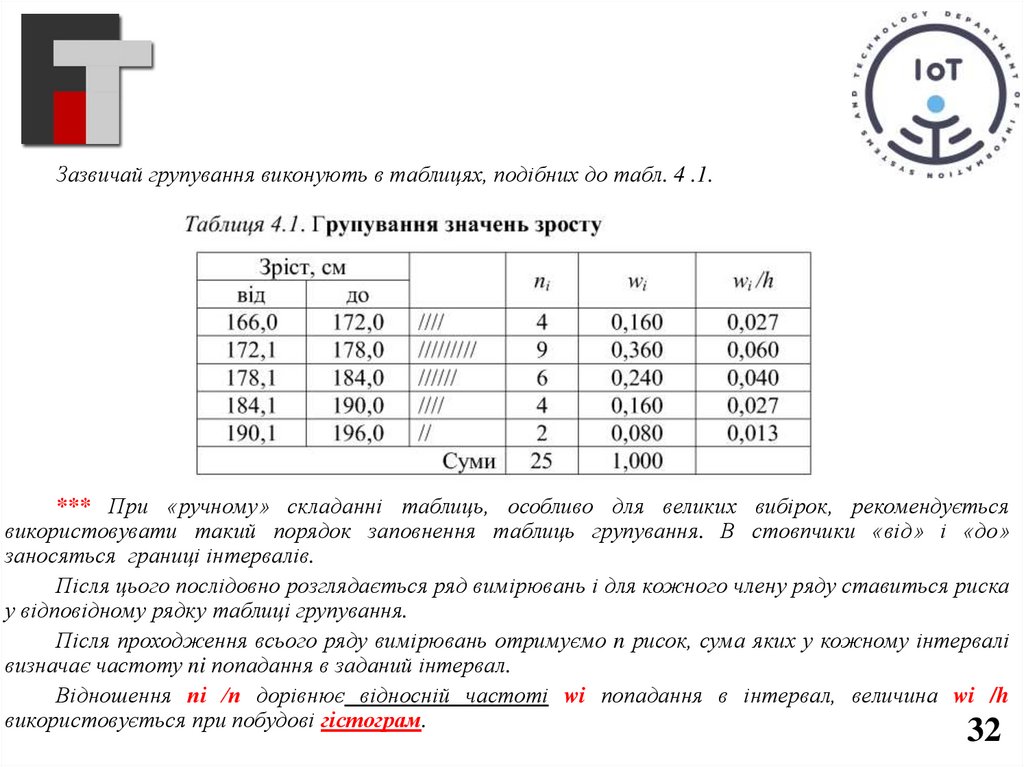
Зазвичай групування виконують в таблицях, подібних до табл. 4 .1.
*** При «ручному» складанні таблиць, особливо для великих вибірок, рекомендується
використовувати такий порядок заповнення таблиць групування. В стовпчики «від» і «до»
заносяться границі інтервалів.
Після цього послідовно розглядається ряд вимірювань і для кожного члену ряду ставиться риска
у відповідному рядку таблиці групування.
Після проходження всього ряду вимірювань отримуємо n рисок, сума яких у кожному інтервалі
визначає частоту ni попадання в заданий інтервал.
Відношення пі /п дорівнює відносній частоті wi попадання в інтервал, величина wi /h
використовується при побудові гістограм.
32

34.

Варіаційним рядом називається упорядкована за зростанням множина усіх
результатів вимірювань.
*** Статистичними аналогами многокутника розподілу є полігон і
гістограма відносних частот (приклади на рис. 4 .2).
Полігон – це ламана лінія, яка з’єднує точки, абсцисами яких є виміряні
значення (або середини інтервалів групування), а ординатами – відповідні
відносні частоти wi . Сума ординат полігона завжди дорівнює одиниці.
Гістограма – це ступінчаста фігура, що складається з прямокутників, основи
яких співпадають з інтервалами групування, а висоти дорівнюють wi/h , тобто
пропорційні відносним частотам. Сума площ прямокутників дорівнює одиниці.
33

35.

!!! Статистичним аналогом функції розподілу є статистична (емпірична)
функція розподілу
(4.4)
де nх – кількість елементів сукупності, менших від х; n – загальний об’єм
сукупності.
*** Інша назва емпіричної функції – кумулятивна крива (вона відображає
накопичення відносних частот).
!!! Слід зауважити, що для емпіричної функції розподілу мають місце всі
властивості функції розподілу дискретної випадкової величини.
УВАГА!!! Функція щільності розподілу f(x) статистичного аналогу не має.

36.

Тема наступної лекції: «Точкові оцінки параметрів генеральної
сукупності.
розсіяння»
Оцінки
характеристик
положення.
Оцінки
характеристик

37.

Лекцію завершено, дякую за увагу!