Лекция №16. Рекурсия. Программирование рекурсивных алгоритмов

1. Программирование на языке C++

1
Программирование
на языке C++
Рекурсия
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

2. Что такое рекурсия?

Алгоритмизация и программирование, язык C++, 10 класс
2
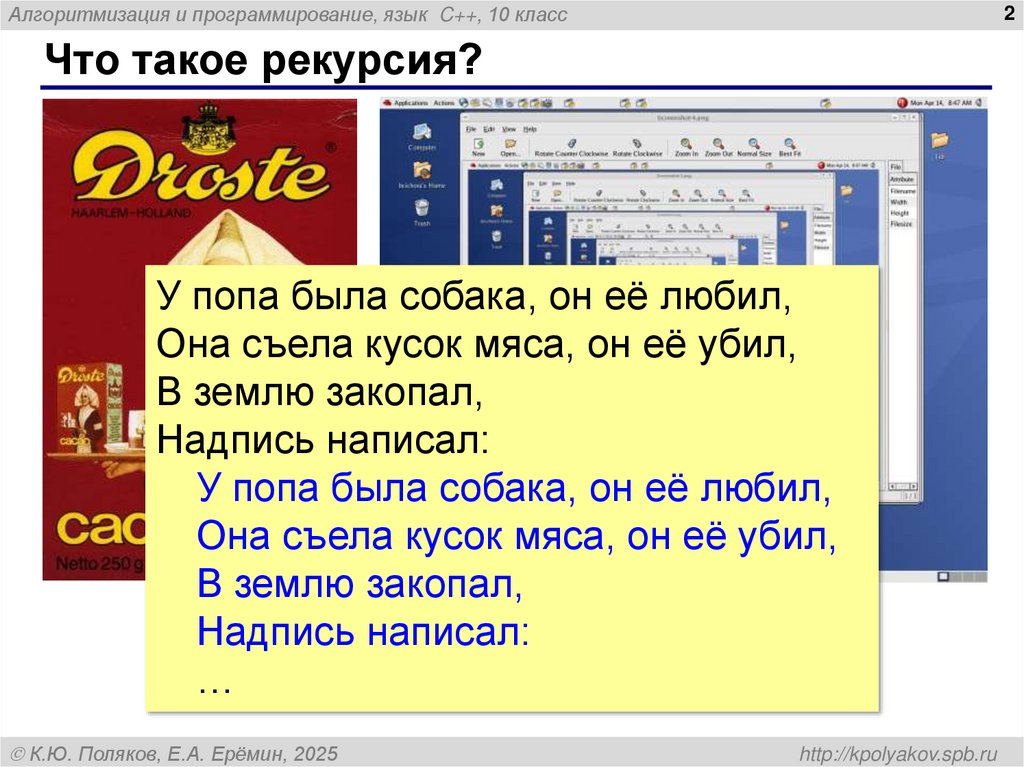
Что такое рекурсия?
У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
…
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

3. Что такое рекурсия?

Алгоритмизация и программирование, язык C++, 10 класс
3
Что такое рекурсия?
Натуральные числа:
• 1 – натуральное число
• если n – натуральное число,
то n 1 – натуральное число
индуктивное
определение
Рекурсия — это способ определения множества
объектов через само это множество на основе
заданных простых базовых случаев.
Числа Фибоначчи:
• F1 F2 1
• Fn Fn 1 Fn 2 при n 2
1, 1, 2, 3, 5, 8, 13, 21, 34, …
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

4. Фракталы

Алгоритмизация и программирование, язык C++, 10 класс
4
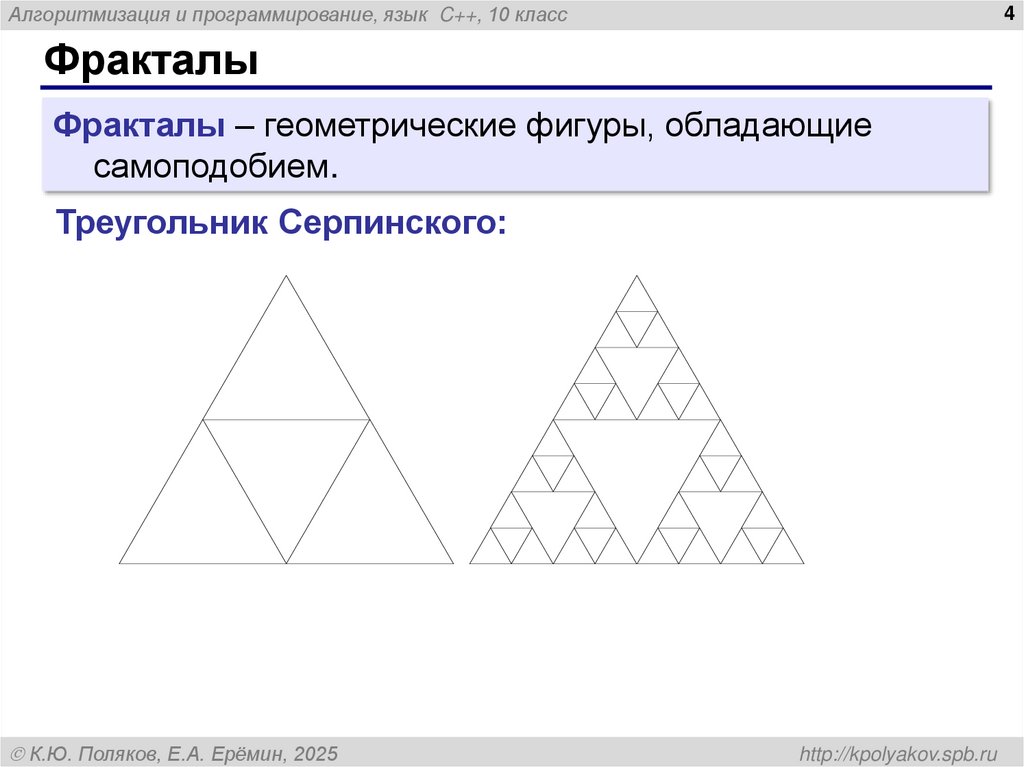
Фракталы
Фракталы – геометрические фигуры, обладающие
самоподобием.
Треугольник Серпинского:
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

5. Ханойские башни

Алгоритмизация и программирование, язык C++, 10 класс
5
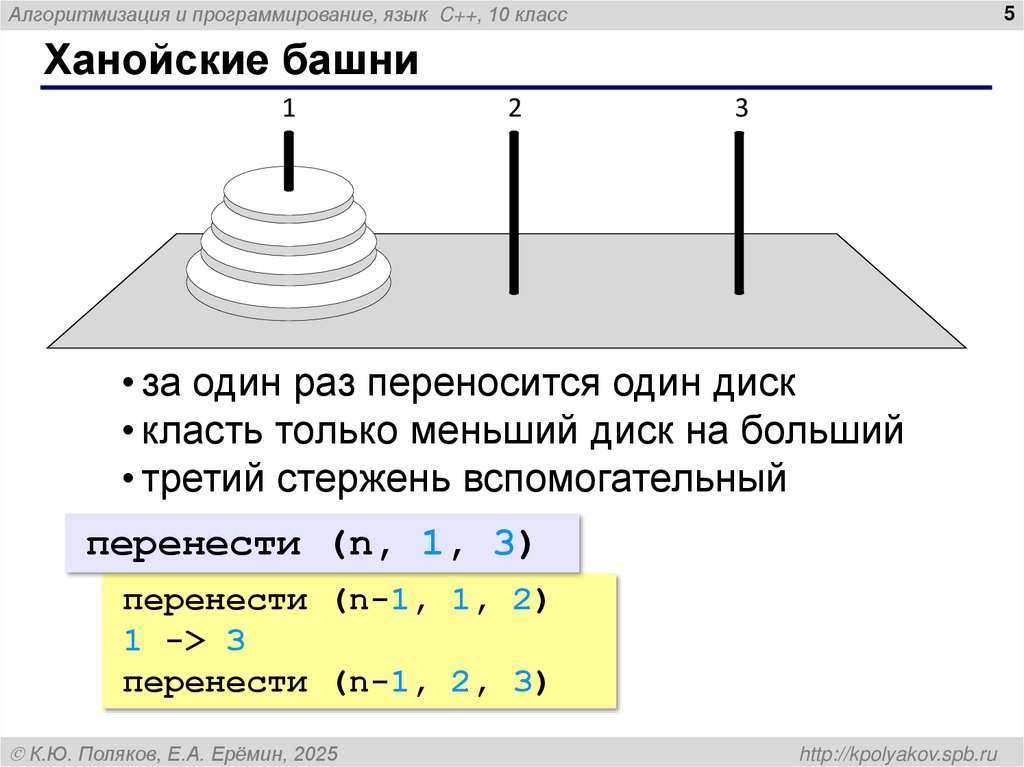
Ханойские башни
1
2
3
• за один раз переносится один диск
• класть только меньший диск на больший
• третий стержень вспомогательный
перенести (n, 1, 3)
перенести (n-1, 1, 2)
1 -> 3
перенести (n-1, 2, 3)
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

6. Ханойские башни – процедура

Алгоритмизация и программирование, язык C++, 10 класс
6
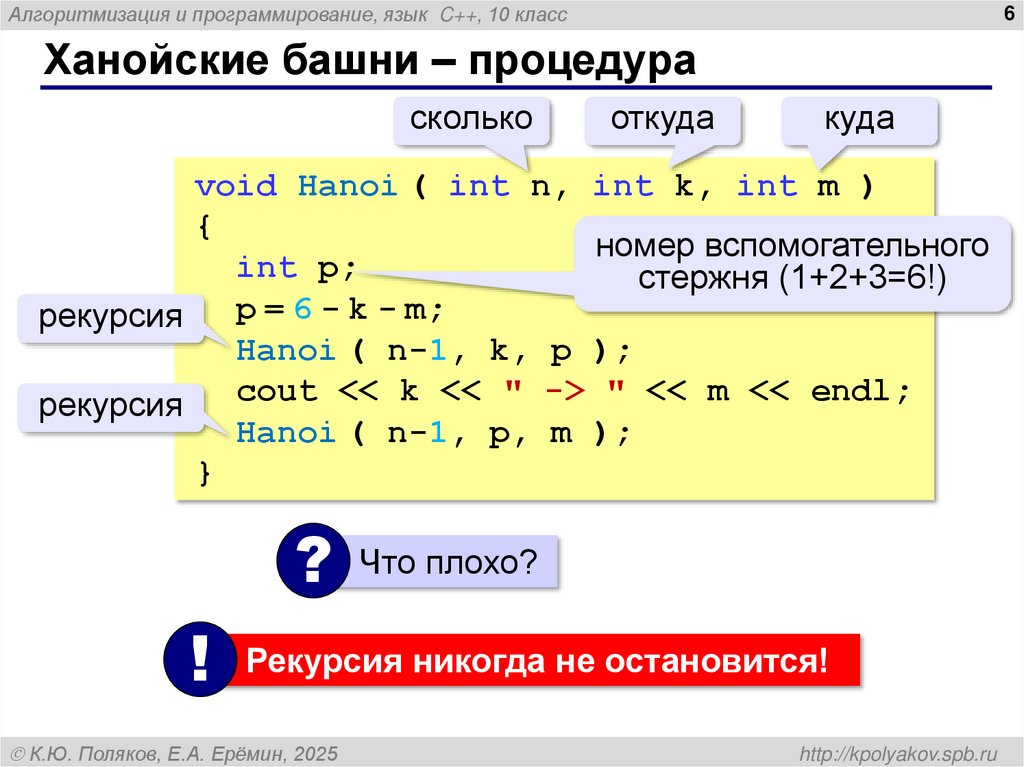
Ханойские башни – процедура
сколько
откуда
куда
void Hanoi ( int n, int k, int m )
{
номер вспомогательного
int p;
стержня (1+2+3=6!)
p = 6 - k - m;
рекурсия
Hanoi ( n-1, k, p );
cout << k << " -> " << m << endl;
рекурсия
Hanoi ( n-1, p, m );
}
? Что плохо?
! Рекурсия никогда не остановится!
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

7. Ханойские башни – процедура

Алгоритмизация и программирование, язык C++, 10 класс
7
Ханойские башни – процедура
Рекурсивная процедура (функция) — это процедура
(функция), которая вызывает сама себя напрямую или
через другие процедуры и функции.
void Hanoi ( int n, int k, int m )
{
условие выхода из
int p;
рекурсии
if ( n == 0 ) return;
p = 6 - k - m;
Hanoi ( n - 1, k, p );
cout << k << " -> " << m << endl;
Hanoi ( n - 1, p, m ); int main()
}
{
Hanoi(4, 1, 3);
}
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

8. Вывод двоичного кода числа

Алгоритмизация и программирование, язык C++, 10 класс
8
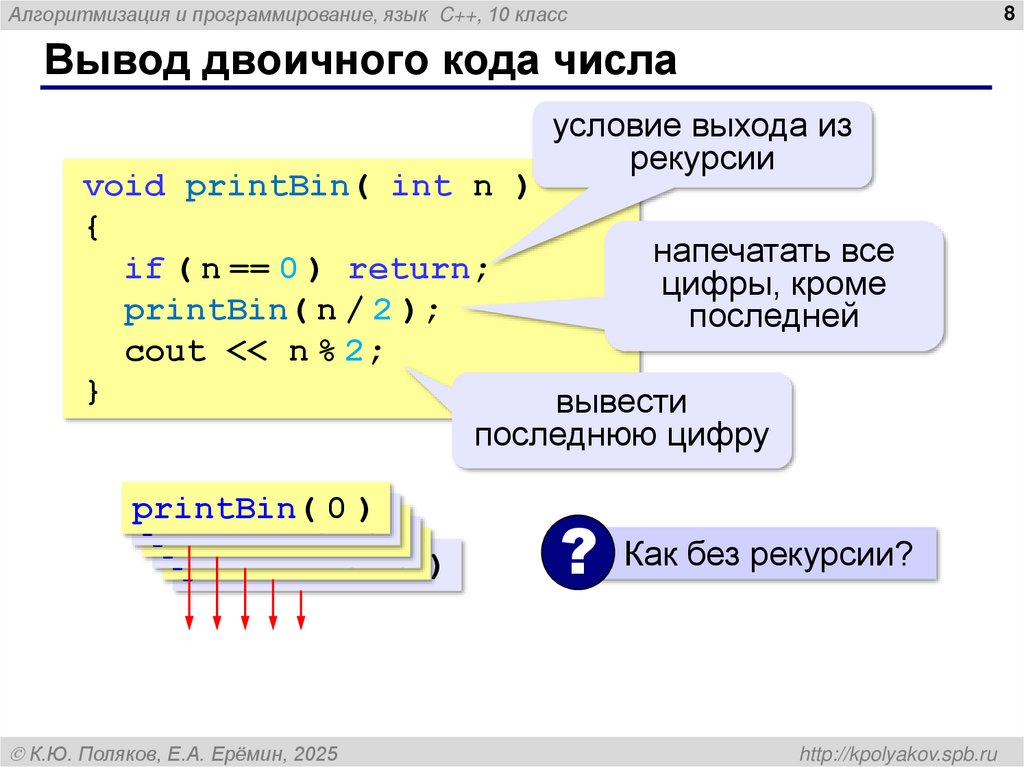
Вывод двоичного кода числа
условие выхода из
рекурсии
void printBin( int n )
{
напечатать все
if ( n == 0 ) return;
цифры, кроме
printBin( n / 2 );
последней
cout << n % 2;
}
вывести
последнюю цифру
printBin(
01))
printBin(
printBin(
24))
printBin(
printBin(
))
printBin(919
? Как без рекурсии?
10011
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

9. Вычисление суммы цифр числа

Алгоритмизация и программирование, язык C++, 10 класс
9
Вычисление суммы цифр числа
Задача. Написать рекурсивную функцию, которая
вычисляет сумму цифр числа.
s = sumDigits( 1234 );
1
2
3
4
n
sumDigits( 123 ) + 4;
n // 10
n % 10
sumDigits( n )= sumDigits( n / 10 )+(n % 10)
sumDigits( n )= n для n < 10
К.Ю. Поляков, Е.А. Ерёмин, 2025
? Это всё?
http://kpolyakov.spb.ru

10. Вычисление суммы цифр числа

Алгоритмизация и программирование, язык C++, 10 класс
10
Вычисление суммы цифр числа
int sumDigits( int n )
{
последняя цифра
int sum;
sum = n %10;
рекурсивный вызов
if ( n >= 10 )
sum += sumDigits ( n / 10 );
return sum;
}
Где условие окончания рекурсии?
?
sumDigits( 1234 )
4 + sumDigits( 123 )
4 + 3 + sumDigits( 12 )
4 + 3 + 2 + sumDigits( 1 )
4 + 3 + 2 + 1
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

11. Вычисление суммы цифр числа

Алгоритмизация и программирование, язык C++, 10 класс
11
Вычисление суммы цифр числа
sumDigits ( 123 );
sum = 3 + sumDigits ( 12 );
sumDigits ( 12 )
sum = 2 + sumDigits ( 1 );
sumDigits ( 1 )
sumDigits = 11 ;
sumnDigits = 3 ;
sumDigits = 6 ;
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

12. Алгоритм Евклида

Алгоритмизация и программирование, язык C++, 10 класс
12
Алгоритм Евклида
Алгоритм Евклида. Чтобы найти НОД двух натуральных
чисел, нужно вычитать из большего числа меньшее до
тех пор, пока меньшее не станет равно нулю. Тогда
второе число и есть НОД исходных чисел.
int NOD ( int a, int b )
{
if ( a == 0 || b == 0 )
условие окончания
рекурсии
return a + b;
if ( a > b )
return NOD( a - b, b );
else return NOD( a, b – a );
}
К.Ю. Поляков, Е.А. Ерёмин, 2025
рекурсивные вызовы
http://kpolyakov.spb.ru

13. Как работает рекурсия?

Алгоритмизация и программирование, язык C++, 10 класс
13
Как работает рекурсия?
Факториал:
1, N 1
N !
N ( N 1)!, N 1
int Fact( int N )
-> N = 3
{
-> N = 2
int F;
-> N = 1
<- N = 1
cout << "-> N=" << N << endl;
<- N = 2
if ( N <= 1 )
<- N = 3
F = 1;
else F = N * Fact(N - 1);
cout << "<- N=" << N << endl;
return F;
}
Как сохранить состояние функции перед
рекурсивным вызовом?
?
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

14. Стек

Алгоритмизация и программирование, язык C++, 10 класс
14
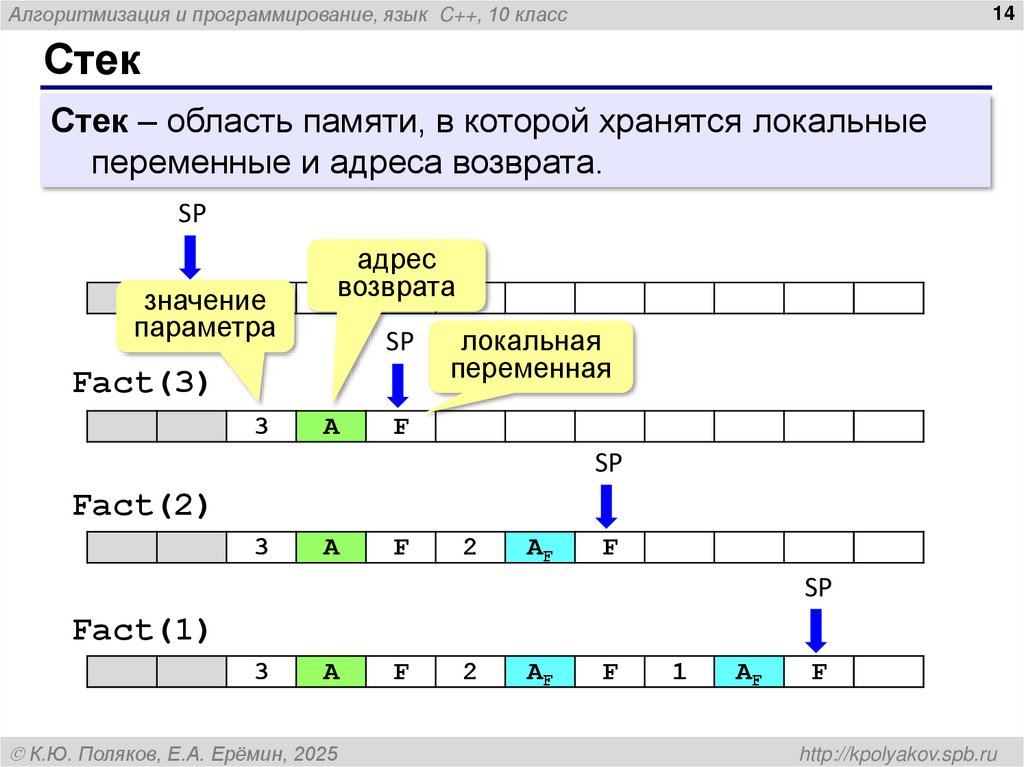
Стек
Стек – область памяти, в которой хранятся локальные
переменные и адреса возврата.
SP
значение
параметра
адрес
возврата
SP
Fact(3)
3
A
локальная
переменная
F
SP
Fact(2)
3
A
F
2
AF
F
SP
Fact(1)
3
A
К.Ю. Поляков, Е.А. Ерёмин, 2025
F
2
AF
F
1
AF
F
http://kpolyakov.spb.ru

15. Рекурсия – «за» и «против»

Алгоритмизация и программирование, язык C++, 10 класс
15
Рекурсия – «за» и «против»
• с каждым новым вызовом расходуется память в стеке
(возможно переполнение стека)
• затраты на выполнение служебных операций при
рекурсивном вызове
программа становится более короткой и понятной
!
возможно переполнение стека
замедление работы
int Fact( int N )
{
Любой рекурсивный
int F;
алгоритм можно заменить
F = 1;
нерекурсивным!
for(i = 2;i <= N;i++)
F = F * i;
итерационный
return F;
алгоритм
}
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

16. Анализ рекурсивных функций

Алгоритмизация и программирование, язык C++, 10 класс
16
Анализ рекурсивных функций
Задача. Определите f(5).
int f( int x ) {
1, x 3
f ( x)
if( x < 3 )
return 1;
f ( x 1) 2,
else
return f( x-1 ) + 2;
}
Метод подстановки:
f(5) = f(4) + 2 = 5 + 2 = 7
f(4) = f(3) + 2 = 3 + 2 = 5
f(3) = f(2) + 2 = 1 + 2 = 3
f(2) = 1
К.Ю. Поляков, Е.А. Ерёмин, 2025
f (5)
f (4)
f (3)
x 3
линейная
структура
f (2)
http://kpolyakov.spb.ru

17. Анализ рекурсивных функций

Алгоритмизация и программирование, язык C++, 10 класс
17
Анализ рекурсивных функций
Задача. Определите f(5).
int f( int x ) {
1, x 3
if( x < 3 )
f ( x)
return 1;
f ( x 1) 2 f ( x 2), x 3
else
return f(x-1) + 2*f(x-2);
}
f (5) 11
дерево
f (3) 3
f (4) 5
3 f (3)
1 f (2)
К.Ю. Поляков, Е.А. Ерёмин, 2025
f (2)
1
f (1) 1
f (2)
1
f (1)
1
http://kpolyakov.spb.ru

18. Анализ рекурсивных функций

Алгоритмизация и программирование, язык C++, 10 класс
18
Анализ рекурсивных функций
Чему равно f (5)?
1, x 3
f ( x)
f ( x 1) 2 f ( x 2), x 3
Табличный метод :
x
f (x)
1
1
2
1
3
3
*2
начальные
значения
К.Ю. Поляков, Е.А. Ерёмин, 2025
4
5
*2
5
11
*2
f(3) = f(2) + 2*f(1) = 3
f(4) = f(3) + 2*f(2) = 5
f(5) = f(4) + 2*f(3) = 11
http://kpolyakov.spb.ru

19. Анализ рекурсивных функций

Алгоритмизация и программирование, язык C++, 10 класс
19
Анализ рекурсивных функций
Задача. Сколько звёздочек выводится при вызове f(11)?
void g( int x ); // объявление функции
void f( int x ) {
if( x > 0 ) g( x-1 );
тут g(x) должна
}
быть известна!
void g( int x ) {
cout << '*';
if( x > 1 ) f( x-3 );
}
f (11)
g(10)
Ответ: 3
*
К.Ю. Поляков, Е.А. Ерёмин, 2025
f (7)
g(6)
*
f (3)
g(2)
f (-1)
*
http://kpolyakov.spb.ru

20. Анализ рекурсивных функций

Алгоритмизация и программирование, язык C++, 10 класс
20
Анализ рекурсивных функций
Задача. Сколько звёздочек выводится при вызове f(9)?
void g( int x ); // объявление функции
void f( int x ) {
if( x > 0 ) {
g( x-1 );
f( x-2 );
1, x 0
f ( x)
}
g ( x 1) f ( x 2) 1, x 0
cout << '*';
}
void g( int x ) {
cout << '*';
if( x > 1 ) f( x-3 );
1, x 1
g ( x)
}
1 f ( x 3), x 1
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

21. Анализ рекурсивных функций

Алгоритмизация и программирование, язык C++, 10 класс
21
Анализ рекурсивных функций
1, x 0
f ( x)
g ( x 1) f ( x 2) 1, x 0
1, x 1
g ( x)
1 f ( x 3), x 1
x
f (x)
g(x)
–1
1
1
0
1
1
1
3
1
2
3
2
3
6
2
4
6
4
5 6 7 8 9
11 11 19 19 32
4 7 7 12 12
f (1) = g(0) + f (–1) + 1 = 3
f (2) = g(1) + f (0) + 1 = 3
Ответ: 32
g (2) = 1 + f (–1) = 2
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru