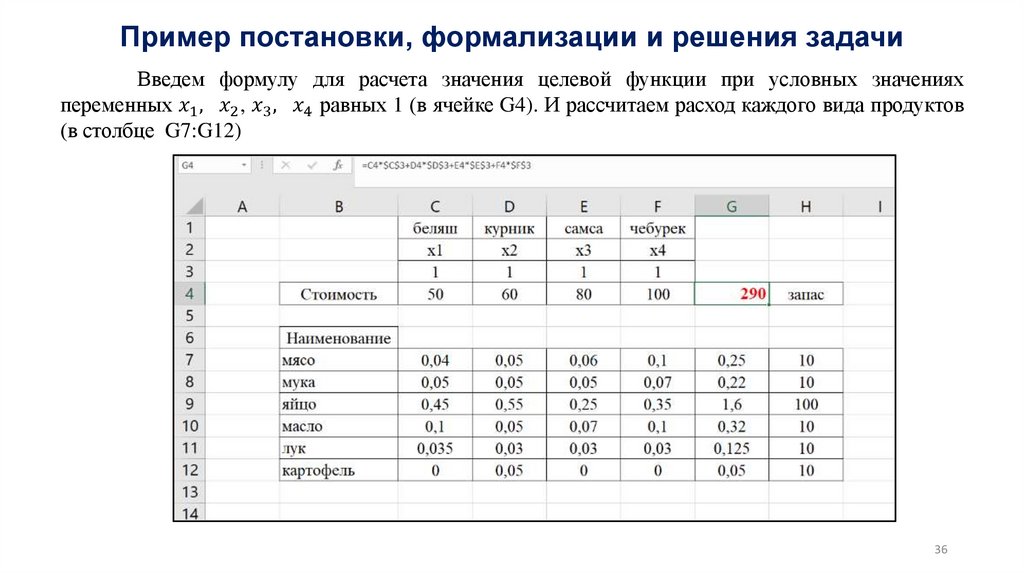
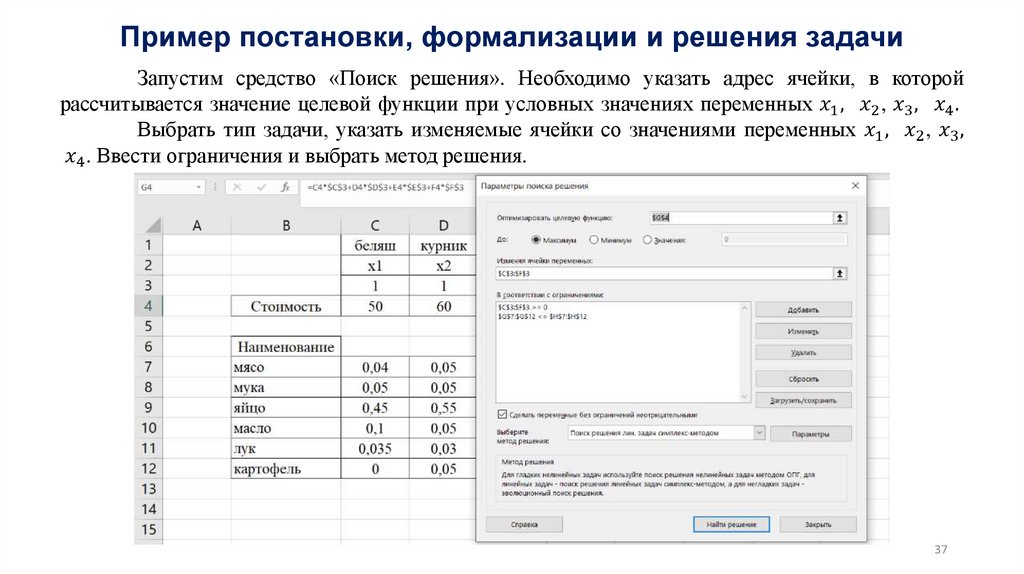
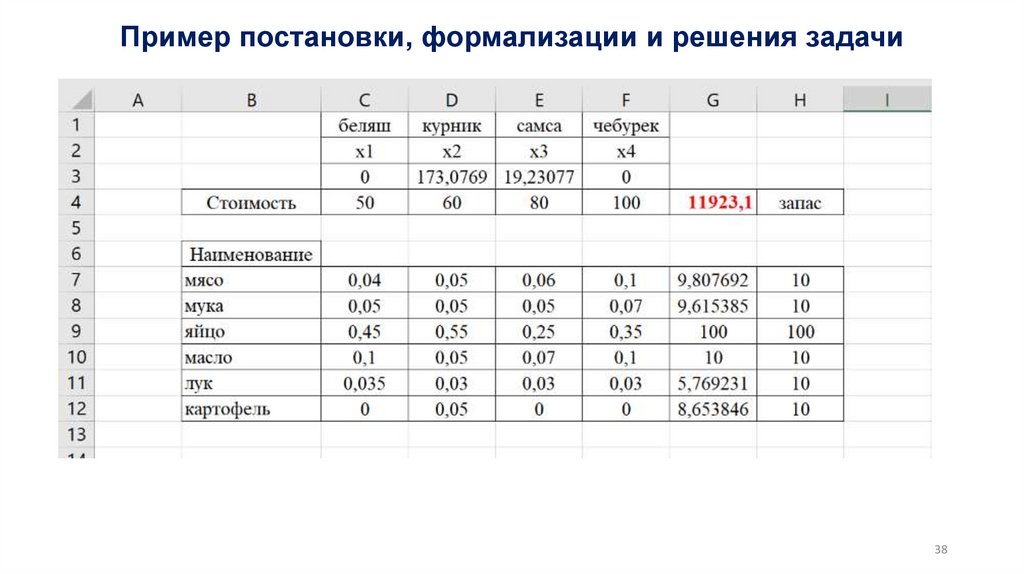
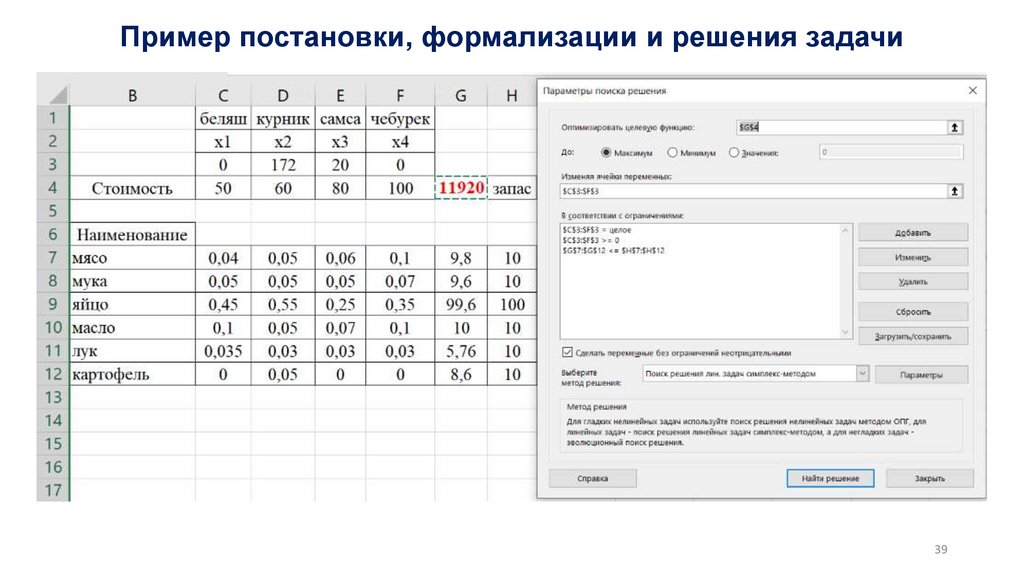
Similar presentations:
Лекция1_Введение в ММПР и ЛП
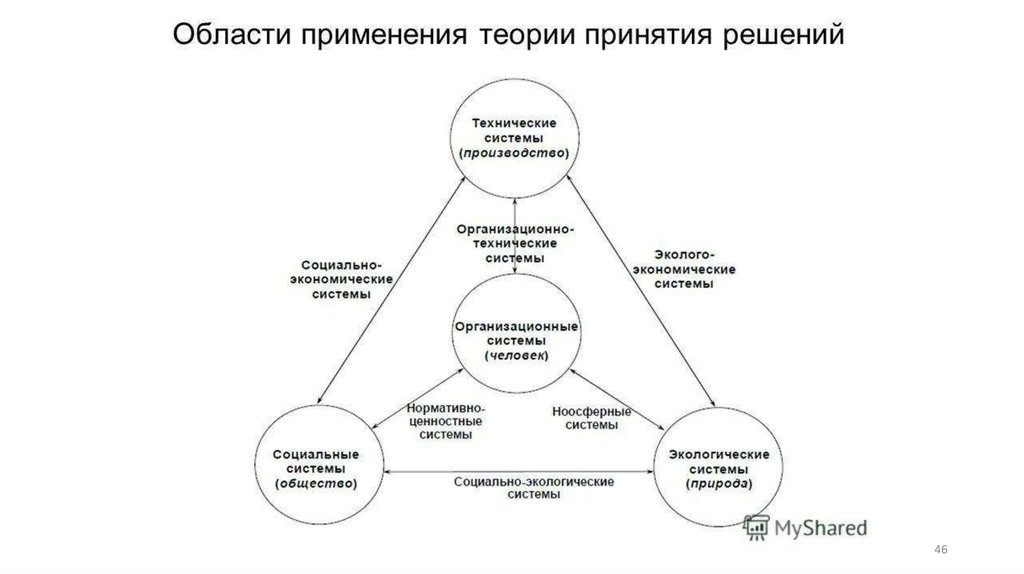
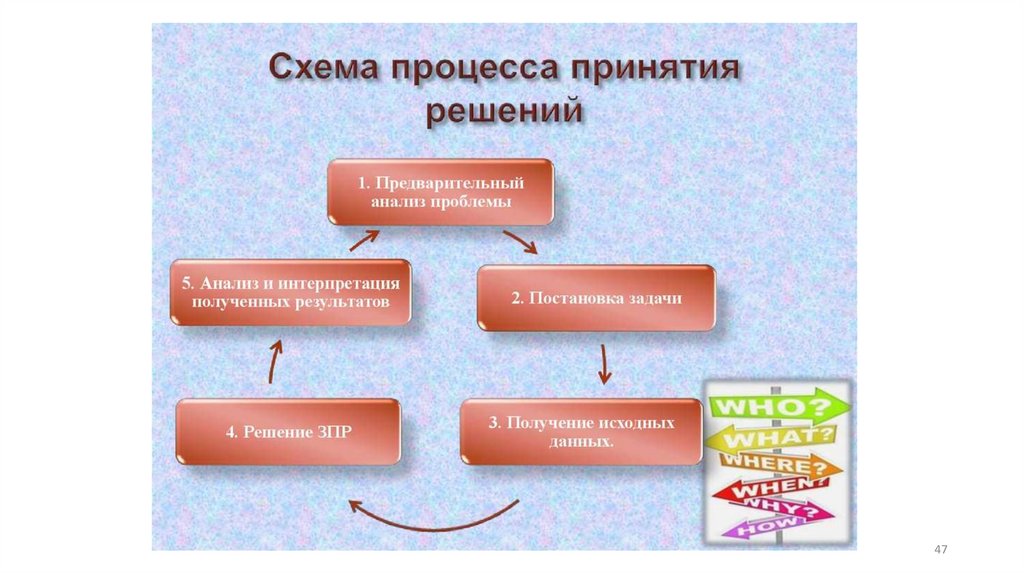
1. Математические и инструментальные методы поддержки принятия решений
Камальдинова Зульфия Фаисовнак.т.н., доцент, доцент кафедры ИСТ
Самара, 2025 год
2. Источники
1. Бодров, В.И. Математические методы принятия решений: учеб. пособие / В.И. Бодров, Т.Я. Лазарева, Ю.Ф.Мартемьянов. – Тамбов: Изд-во Тамб. гос. тех. ун-та, 2004. – 124 с.
2. Есипов, Б.А. Методы оптимизации и исследование операций: учеб. пособие / Б.А. Есипов. - Самара: Изд-во
Самар, гос. аэрокосм, ун-та, 2007. - 180 с.
3. Гераськин, М.И. Системы поддержки принятия решений для оптимизации управления предприятием
методами линейного программирования: учеб. пособие / М. И. Гераськин, Л. С. Клентак. – Самара: Изд-во
Самарского университета, 2018. – 148 с.
4. Грешилов, А.А. Математические методы принятия решений: учеб. пособие (с расчётными программами на
оптическом диске) / А. А. Грешилов. – 2-е изд., испр и доп. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2014.—
647 с.
5. Ларичев О. И. Теория и методы принятия решений, а также Хроника событий в Волшебных странах:
учебник. - М.: Логос, 2000. – 296 с.
6. Линейное и нелинейное программирование. Динамическое программирование. Элементы теории игр.
Сетевое планирование: лабораторный практикум / Сост. М.А. Евдокимов, Л.Н. Смирнова, Т.А. Бенгина, Т.Н.
Кочетова, О.В. Филиппенко. – Самара: Самар. гос. техн. ун-т, 2014. – 99 с.
7. Лиманова, Н.И. Математические и инструментальные методы поддержки принятия решений: учеб. Пособие
/ Н.И. Лиманова. – Самара: ИУНЛ ПГУТИ, 2019. – 225 с.
2
3. Источники
34. Источники
45. Источники
56. Источники
67. Источники
78. Источники
89. Источники
910. Источники
1011. Источники
1112. Источники
1213. Источники
Статьи на портале https://habr.com/ru/companies/habr/profile/13
14. Источники
1415. Курсовое проектирование
1516. Инструментальные средства
R предлагает набор пакетов с открытым исходным кодом, которые подходят для различныхколичественных и статистических задач.
Это включает в себя поддержку нейронных сетей, нелинейной регрессии, филогенетики,
создание сложных диаграмм, графиков и многое другое. Кроме того, вместе с базовой
установкой R предоставляет встроенные функции и методы, а также обрабатывает данные
матричной алгебры. Для визуализации данных используются библиотеки.
Ограниченность области применения - R хорошо подходит для статистических
исследований и науки о данных, но может быть менее подходящим для общих программных
задач.
Python является востребованным и широко используемым языком программирования
общего назначения. Он предлагает обширный набор специально разработанных
модулей и широко используется в различных областях разработки.
Он очень легко изучается, что делает его идеальным вариантом для начинающих
программистов.
Наличие таких пакетов, как pandas, scikit-learn и Tensorflow, делает Python
надежным выбором для разработки современных приложений в области машинного
обучения.
Недостаток типобезопасности - Python является динамически типизированным
языком, поэтому необходимо быть осторожным при работе с ним, чтобы избежать
ошибок типов.
16
17. Инструментальные средства
SQL или «язык структурированных запросов», используется для определения, управления и запросареляционных баз данных. SQL является эффективным инструментом для работы с запросами,
обновлениями и обработки реляционных баз данных. Использование декларативного синтаксиса
делает SQL читаемым языком.
SQL широко используется в различных приложениях, поэтому знание этого языка может быть очень
полезным. Модули, такие как SQLAlchemy, упрощают интеграцию SQL с другими языками.
Синтаксис SQL может показаться сложным для тех, кто привык к императивному стилю
программирования.
Java является популярным языком программирования общего назначения, который работает
на виртуальной машине Java Virtual Machine (JVM). Эта абстрактная вычислительная система
обеспечивает переносимость между различными платформами и поддерживается
корпорацией Oracle.
Java обладает универсальностью, и многие современные системы и приложения разработаны
на этом языке. Его преимуществом является возможность интеграции методов науки о
данных в существующий код. Строгая типизация придает Java надежность и безопасность.
Из-за своей «многословности» Java не является лучшим выбором для специальных анализов
и разработки статистических приложений. Отсутствие большого количества библиотек для
статистических методов делает Java менее привлекательным по сравнению с некоторыми
другими языками, например R.
17
18. Инструментальные средства
Scala - это язык программирования, который объединяет объектно-ориентированный ифункциональный подходы и используется в структуре кластерных вычислений Apache
Spark.
Используя Scala и Spark, вы можете работать с высокопроизводительными кластерными
вычислениями, что особенно полезно для обработки больших объемов данных.
Начинающим программистам может потребоваться время и усилия для освоения Scala.
Синтаксис и система типов Scala могут показаться сложными для программистов,
привыкших к динамическим языкам, например Python.
Julia - это язык программирования, который был выпущен после 2010 и сразу привлек
внимание в области вычислительных методов. Он стал популярным благодаря
использованию несколькими крупными организациями, включая финансовую отрасль.
Julia - это скомпилированный язык JIT («точно в срок»), который обеспечивает хорошую
производительность. Он является относительно простым языком, поддерживает
динамическую типизацию и имеет функциональность интерпретируемого языка,
например Python.
Недостаток зрелости. Поскольку Julia является относительно новым языком, некоторые
разработчики могут столкнуться с нестабильностью при работе с его пакетами. Однако,
базовые функциональности языка считаются стабильными.
18
19. Инструментальные средства
MATLAB – это признанный язык, который широко используется для численных расчетов как внаучных, так и в промышленных целях. Он имеет лицензию от компании MathWorks.
MATLAB подходит для численных расчетов и используется для сложного количественного анализа,
такого как обработка сигналов, преобразования Фурье, матричная алгебра и обработка
изображений. Он также предоставляет удобные возможности визуализации данных, включая
построение графиков и диаграмм.
Использование MATLAB требует покупки лицензии, а стоимость зависит от выбранного варианта
использования. MATLAB не является лучшим языком программирования для общих задач.
C++. Редко используется в области науки о данных из-за неэффективности, но обладает высокой производительностью и
популярностью. C++ может быть полезен для реализации оптимизированных низкоуровневых алгоритмов машинного
обучения.
JavaScript приобретает черты серверного языка благодаря развитию платформы Node.js, но его возможности в области
науки о данных все еще ограничены. JavaScript имеет преимущества, такие как асинхронный ввод-вывод, растущая
популярность и возможность компиляции на другие языки программирования.
Perl - является универсальным языком сценариев общего назначения, но он не имеет такой популярности в области науки
о данных, как Python. Perl может быть полезен в биоинформатике и количественном анализе, но его синтаксис считается
недружелюбным.
Ruby - динамически типизированный язык общего назначения, который не так широко используется в науке о данных, как
Python. Хотя существуют проекты, такие как SciRuby, созданные для внедрения научных вычислений в Ruby.
19
20. Дисциплины и связи
Математическая статистика - разрабатываются математические методы систематизации иобработки экспериментальных данных с целью изучения закономерностей массовых случайных
явлений и использования их для научных и практических выводов.
Исследование операций - методология анализа сложных систем, их математическое
моделирование и нахождение на этой основе наилучших (оптимальных) решений в общем виде.
Методы оптимизации – математические методы нахождения экстремумов функций и
функционалов, когда математическая модель задачи уже сформулирована.
Линейное программирование - наука о методах исследования и отыскивания наибольших и
наименьших значений линейной функции, на неизвестные которой наложены линейные
ограничения.
Теория принятия решений - широкий класс проблем, связанный с принятием решений, которые
не удается свести к традиционным задачам нахождения экстремума. В этих задачах не всегда
удается априорно перечислить варианты возможных решений, в них может быть множество
противоречивых критериев, то есть таких, удовлетворить которым одновременно нельзя.
Наконец, в самой формулировке цели, ради которой принимается решение, появляется элемент
неопределенности, задача иногда формулируется в самом общем виде. Возникают сложности с
определением списка критериев, по которым должно быть оптимизировано решение, а также
важности этих критериев относительно друг друга.
20
21. Учёные
Леонид ВитальевичКанторович
Лев Семёнович
Понтрягин
Альберт
Уильям
Таккер
Никита Николаевич
Моисеев
Ричард
Эрнест
Бе́ллман
Джордж Бернард
Да́нциг
Гарольд Уильям
Кун
Ральф
Эдуард
Гомори
21
22. Учёные
Леонид Витальевич Канторович - принадлежит к числу самых выдающихся отечественныхматематиков и экономистов XX столетия. Принципы линейного программирования,
разработанные им в 1930-е гг., нашли широкое применение при моделировании
производственных задач и хозяйственного планирования. Система оптимального
распределения ресурсов, найденная с помощью математического аппарата, принесла
Канторовичу единственную Нобелевскую премию по экономике среди советских и
российских учёных
Лев Семёнович Понтрягин. Внёс значительный вклад в алгебраическую и
дифференциальную топологию, теорию колебаний, вариационное исчисление, теорию
управления. В теории управления Понтрягин — создатель математической теории
оптимальных процессов, в основе которой лежит т. н. принцип максимума Понтрягина;
имеет фундаментальные результаты по дифференциальным играм. Работы школы
Понтрягина оказали большое влияние на развитие теории управления и вариационного
исчисления во всём мире.
22
23. Учёные
Никита Николаевич Моисеев. Основоположник целого ряда новых направлений вприкладной математике. Автор работ по механике и гидродинамике, численным
методам в теории оптимального управления, теории иерархических систем,
имитационному моделированию, автоматизации проектирования, междисциплинарным
исследованиям экологических проблем. В каждой из этих областей Моисееву
принадлежат основополагающие достижения
Джордж Бернард Да́нциг — американский математик, известен как разработчик
алгоритма, применяемого в решениях задач симплекс-методом. Считается
основоположником линейного программирования, наряду с Леонидом
Канторовичем и Джоном фон Нейманом
23
24. Учёные
Гарольд Уильям Кун— американский математик, специалист по теории игр. Лауреатпремии Джона фон Неймана за 1980 год совместно с Альбертом Таккером и Дэвидом
Гэйлом. Заслуженный профессор математики в Принстонском университете, известен
как автор теоремы Куна, покера Куна, а также как соавтор условия Куна-Таккера. Дал
описание венгерского алгоритма для решения задачи о назначениях.
Альберт Уильям Таккер — канадский математик, внесший важный вклад в развитие
топологии, теории игр и нелинейного программирования. В 1950 году дал название
и формулировку для одного из самых известных теоретико-игровых парадоксов —
«дилеммы заключенного», сформулированного Мерилом Фладом и Мелвином
Дрешером в рамках своей модели сотрудничества и конфликта. Он также известен
как один из авторов условий Куна-Таккера, играющих важную роль в нелинейном
программировании.
24
25. Учёные
Ричард Эрнест Бе́ллман — американский математик, один из ведущихспециалистов в области математики и вычислительной техники. Получил
многочисленные результаты, связанные с применением динамического
программирования в разных областях математики (вариационное
исчисление, автоматическое регулирование, теория аппроксимации,
исследование операций и др.). В 1979 году он был награждён медалью
почёта IEEE «за вклад в теорию процессов принятия решений и теорию
управления системами, особенно за создание и применение
динамического программирования».
Ральф Эдуард Гомори (сейчас 96 лет) — американский математик и
менеджер. Гомори работал в должности исследователя в компании IBM, а
затем стал её руководителем. Его вклад позволил открыть новые области
прикладной математики. Алгоритм Го́мори — алгоритм, который
используется для решения полностью целочисленных задач линейного
программирования.
25
26. Математическое программирование
Математическое программирование — это математическая дисциплина, вкоторой изучают теорию и методы решения задач о нахождении экстремумов
функций на множествах, определяемых линейными и нелинейными
ограничениями в виде равенств и не равенств.
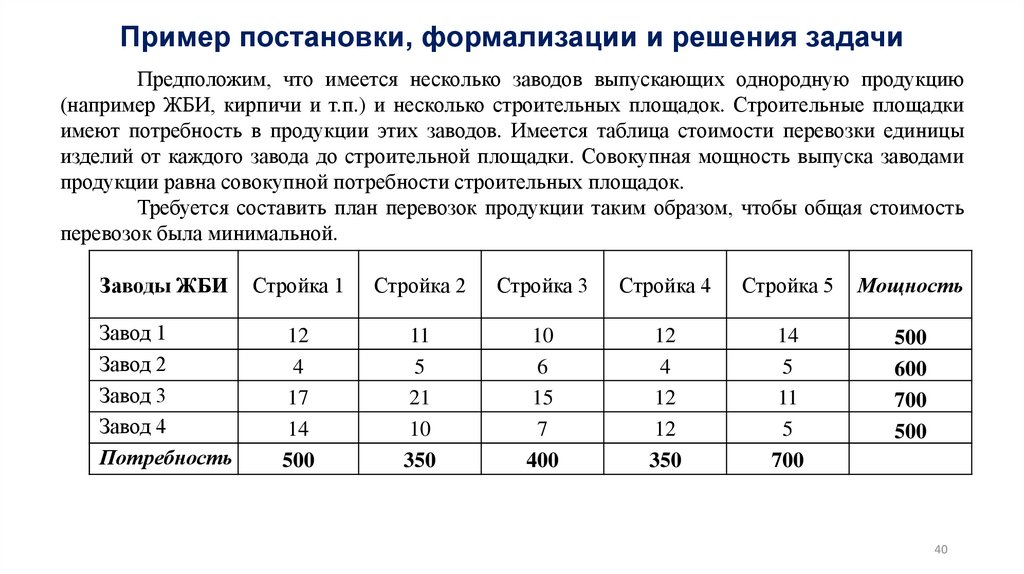
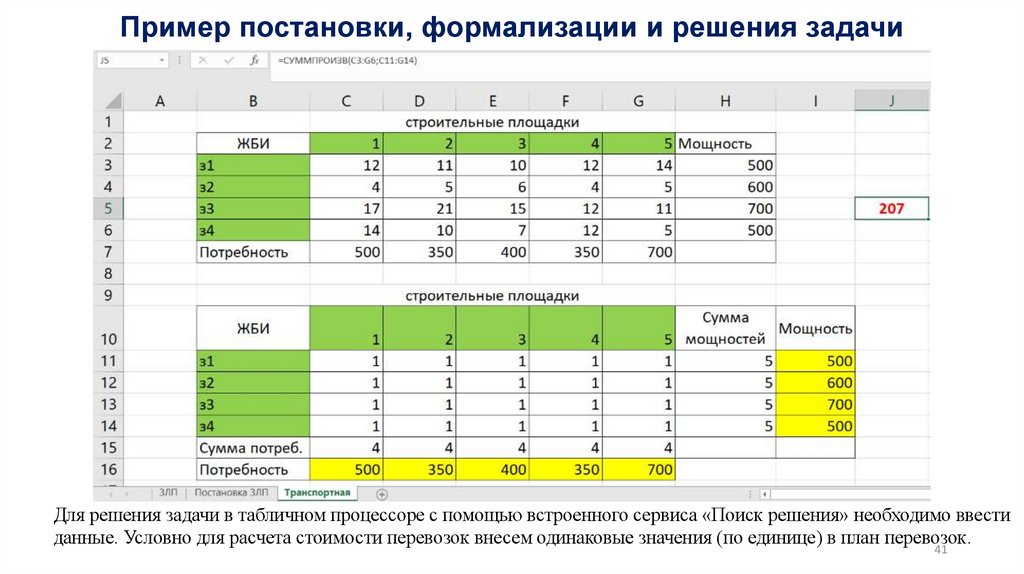
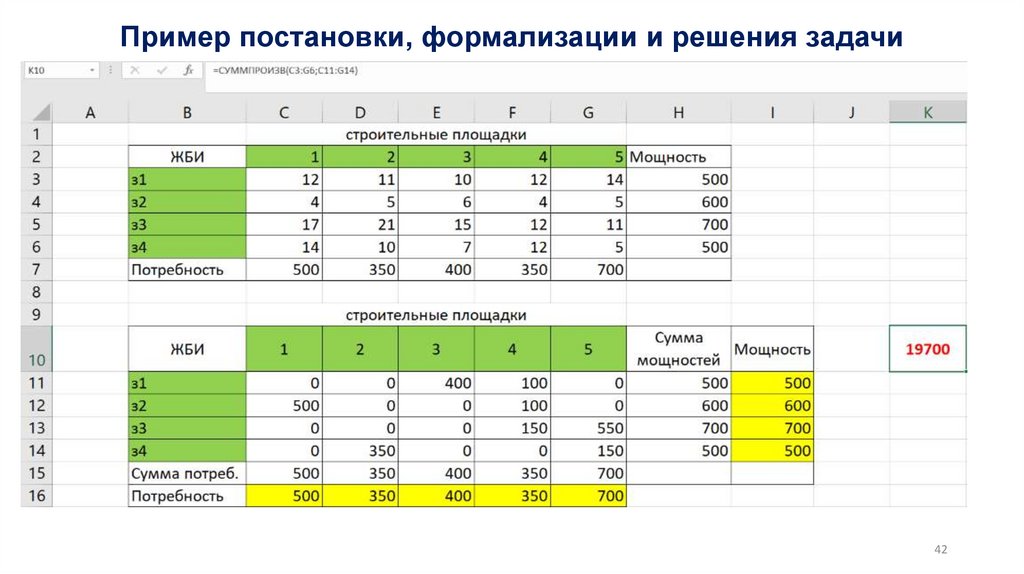
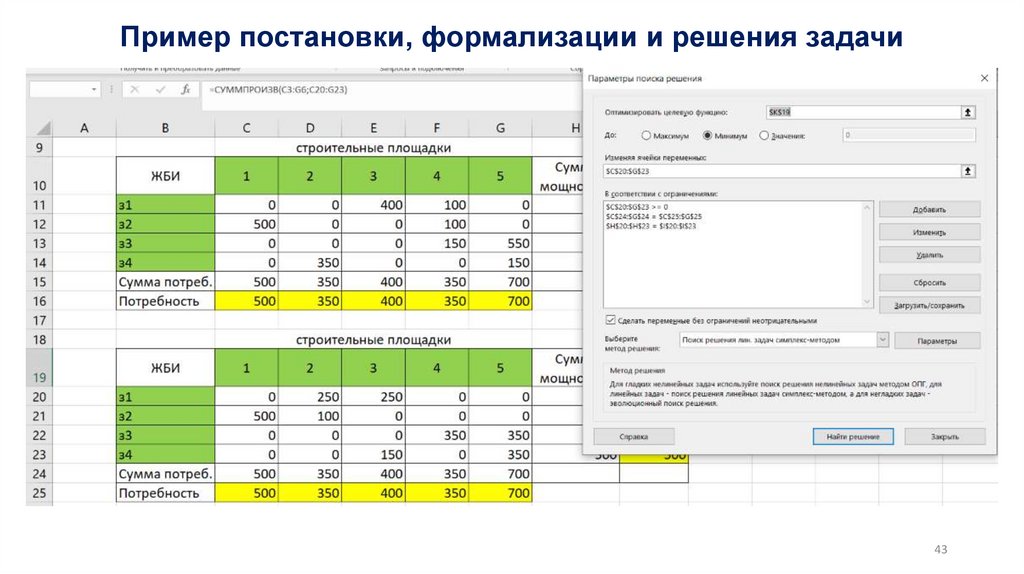
1. Задача о диете, о рационе питания, распределение ресурсов, план производства
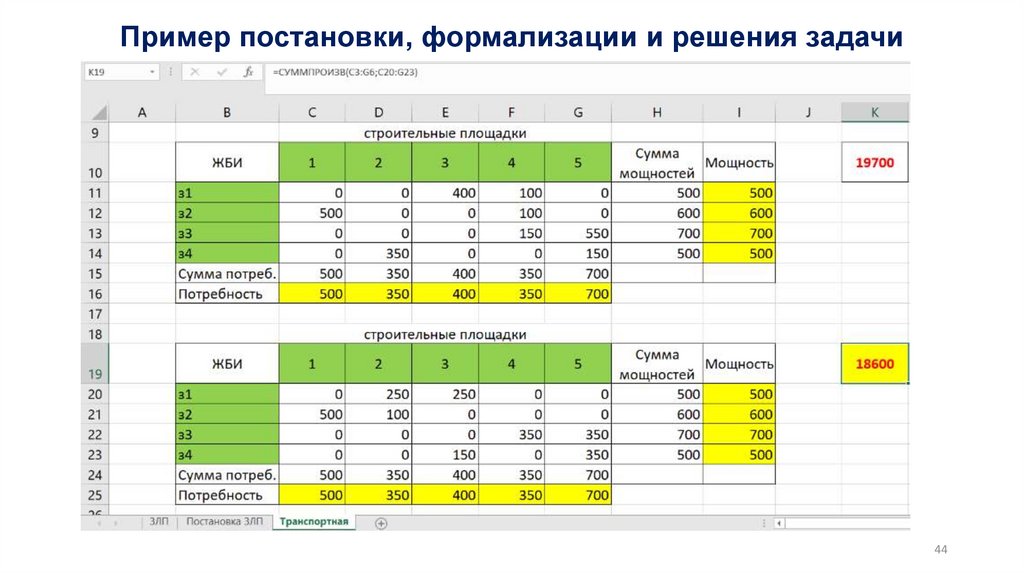
2. Транспортная задача
1) разработка методов управления техникой, обеспечивающих достаточно высокий
уровень эффективности деятельности людей;
2) разработка методов использования имеющейся в распоряжении людей техники,
обеспечивающей выполнение поставленной задачи с минимальными затратами или с
максимальным эффектом;
3) разработка техники и материалов, которые необходимо создать или приобрести в
рамках общей стратегии деятельности людей.
26
27. Математическое программирование
1. Изучение объекта. Анализ особенностей функционирования объекта; определение факторов,оказывающих на это влияние (их количество и степени влияния); изучение характеристик объекта
при различных условиях; выбор оптимизируемого критерия (целевой функции).
2. Описательное моделирование. Установление и фиксация основных связей и зависимостей между
характеристиками процесса или явления согласно оптимизируемому критерию.
3. Математическое моделирование. Запись описательной модели математическими формулами.
Все условия записывают в виде соответствующей системы равенств и неравенств, а критерий
оптимизации — в виде функции.
4. Выбор или создание метода решения. Исходя из полученной математической записи задачи
выбирают либо известный метод решения, либо некую модификацию известного метода, либо
разрабатывают новый метод решения.
5. Выбор или написание программы для решения задачи на ЭВМ. Задачи, как правило, имеют много
переменных и много зависимостей {уравнений связи) между ними. Поэтому в разумные сроки они
могут быть решены только с помощью ЭВМ.
6. Решение задачи на ЭВМ.
7. Анализ полученного решения. Анализ решения бывает формальным и содержательным.
8. Анализ устойчивости решения. Аналитически или с помощью численных методов исследуют
поведение решения при не больших (в пределах возможных погрешностей или
неопределенностей) изменениях исходных данных.
27
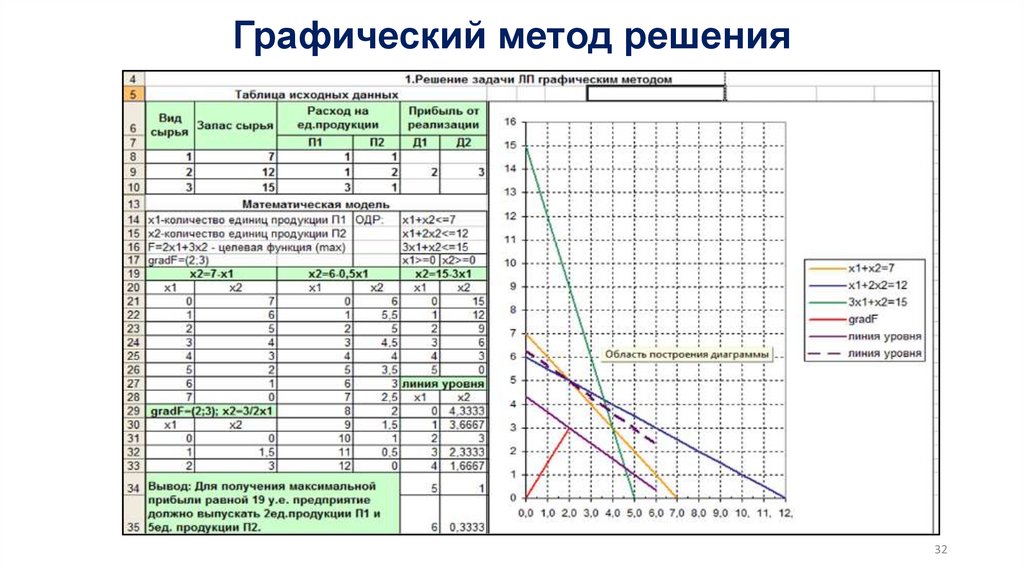
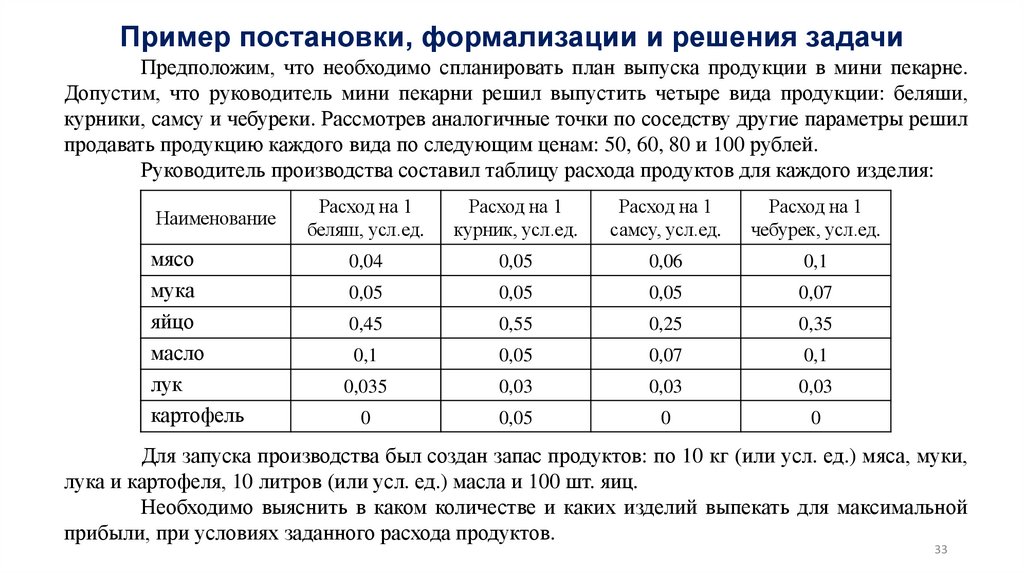
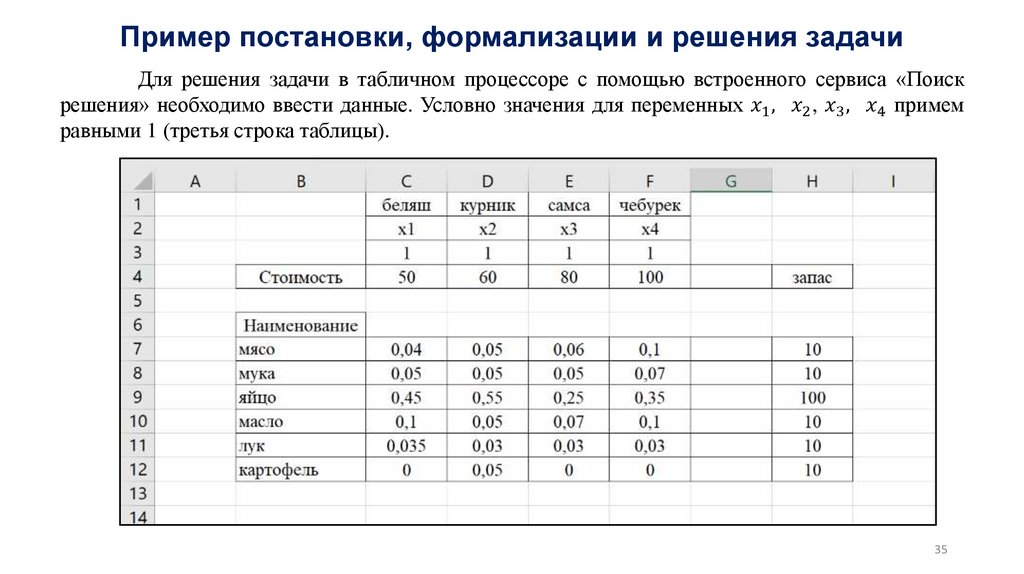
28. Линейное программирование
Линейное программирование является составной частью задач математическогопрограммирования, в которых критерий оптимальности задается в виде линейной функции от
входящих в него переменных, кроме того, на эти переменные накладываются некоторые
ограничения в форме линейных равенств и неравенств.
Типовые задачи линейного программирования
Задача об оптимальном выпуске продукции
Пусть предприятие выпускает n наименований продукции.
Затраты i-го вида ресурсов (i =1,