Мат. ожидание геом. и бином. распред_8.11.25

1. 8.11.25 Классная работа

2.

Математическое ожидание
геометрического и биномиального
распределений.

3. Проверка д/з на 8.11.25

1.
2.

4. Проверка д/з на 8.11.25

3.
4.

5. Устная работа

1.
2.
3.
4.

6.

Математическое ожидание и
закон больших чисел
Закон больших чисел связан с обработкой статистических
данных. Он применяется в разных сферах человеческой
деятельности: в инвестировании, здравоохранении, сфере
страхования — везде, где нужно анализировать массив
информации.
Если сформулировать закон больших чисел простыми
словами, то это закон, позволяющий понять, каким
вероятнее всего окажется результат эксперимента, если
проводить его неоднократно. Чем большим будет число
таких экспериментов, тем ближе будет результат к
математическому ожиданию.

7.

Термин «математическое ожидание» введен Пьером Лапласом в
1795 г. и произошел от понятия «ожидаемое значение выигрыша»,
впервые появившегося в XVII в. в теории азартных игр в
трудах Блеза Паскаля и Христиана Гюйгенса.
Математическое ожидание — чрезвычайно полезный инструмент,
используемый при принятии любых управленческих решений,
особенно в сфере финансов.
Под ним понимается усредненное значение случайной величины.
Оно рассчитывается как среднее значение выпавшего
результата на определенной выборке, его величина зависит от
этой выборки.
Закон больших чисел показывает, насколько близким окажется
среднее значение выборки к математическому ожиданию для
одного и того же распределения.

8. Как использовать закон больших чисел и математическое ожидание?

Одно из применений закона больших чисел —
прогнозирование результатов:
• объемов продаж (в качестве базы для прогноза берутся результаты
прошлых отчетных периодов),
• страховой премии (в долгосрочном периоде даже несчастные
случаи подчиняются закону),
• ставок по кредиту (для покрытия убытков при невыплате займов),
• средней заболеваемости для выработки норм снабжения
медучреждений.

9. Как использовать закон больших чисел и математическое ожидание?

Кроме того, закон больших чисел применяют для описания фаз
развития бизнеса. Например, из него следует, что темпы роста
бизнеса не могут быть постоянными неограниченно долго.
Математическое ожидание является эффективным способом
выявить прибыльность выбранной ниши бизнеса.
Собрав свою статистику, можно рассчитать математическое
ожидание, которое может быть как положительным, так и
отрицательным.
Если значение математического ожидания положительное, это
значит, что бизнес стабильно прибылен.
Отрицательное значение показывает, что в случае продолжения
такой ситуации прибыль окажется ниже ожидаемого значения,
можно понести потери.

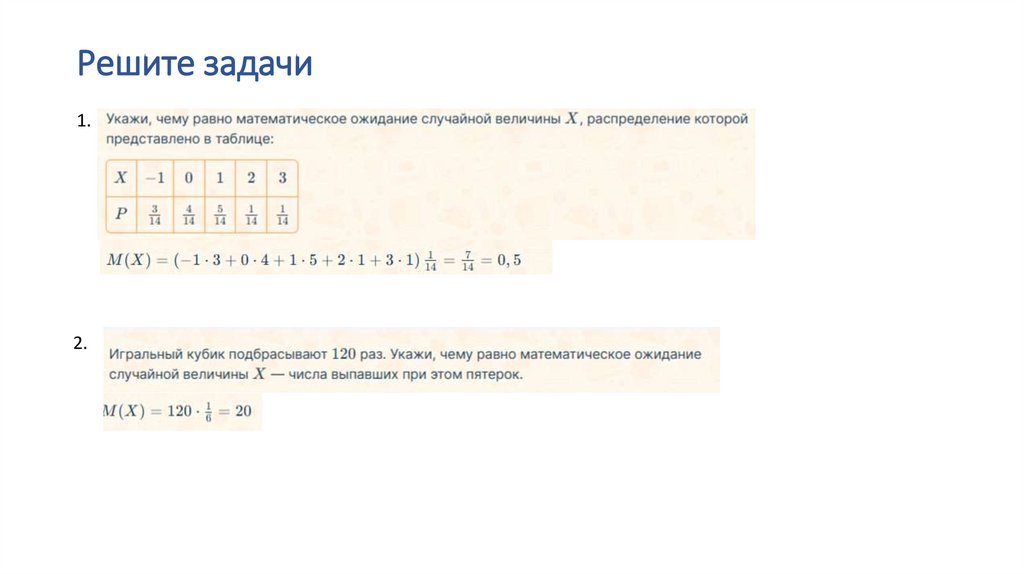
10. Решите задачи

1.
2.

11. Решите задачи

3.
4.

12. Решите задачи

4.

13. Решите задачи

5.
Повышенный уровень

14. Решите задачи

6.
Повышенный уровень

15. Решите задачи

7.
Повышенный уровень

16. Решите задачи

8.
Повышенный уровень

17. Задания для самостоятельной работы:

1.
2.
3.
4.

18. Д/з на 15.11.25