Г-11 урок 21.11.25 новая тема

1.

2. Цель:

11.1.6 - знать определение
правильного
многогранника,
распознавать виды
правильных
многогранников.

3. Правильных многогранников вызывающе мало… Л.Кэролл

Выпуклый многогранник называется
правильным , если все его граниравные правильные многоугольники ,и
в каждой его вершине сходится
одинаковое количество ребер.

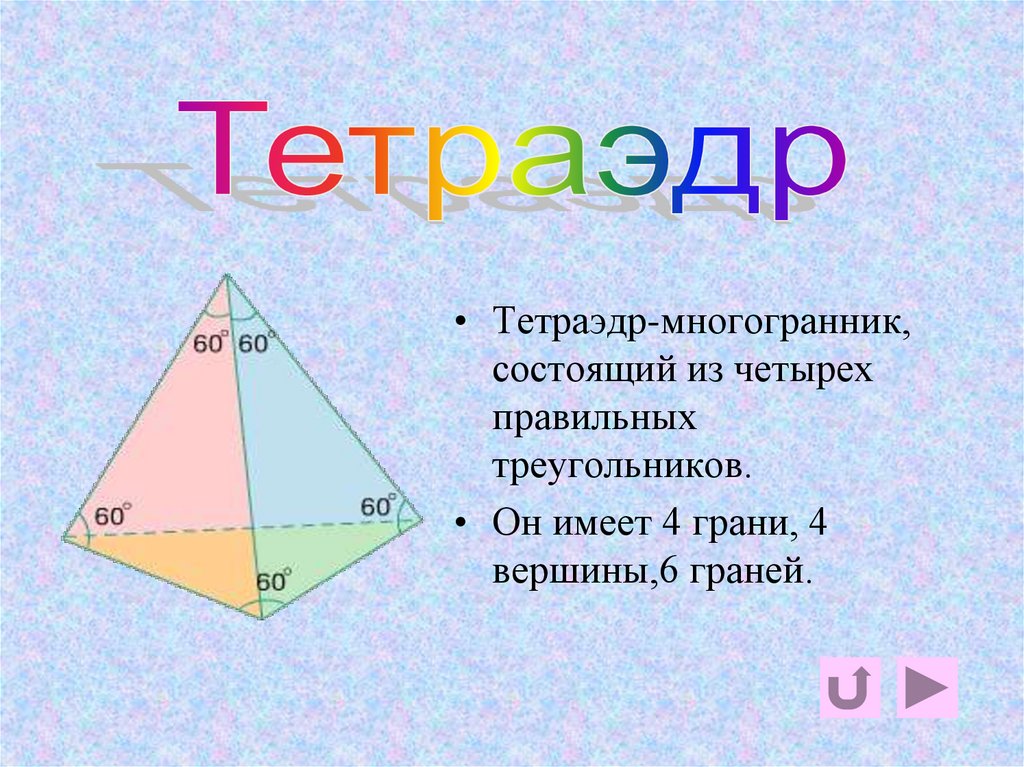
4. тетраэдр

• Тетраэдр-многогранник,
состоящий из четырех
правильных
треугольников.
• Он имеет 4 грани, 4
вершины,6 граней.

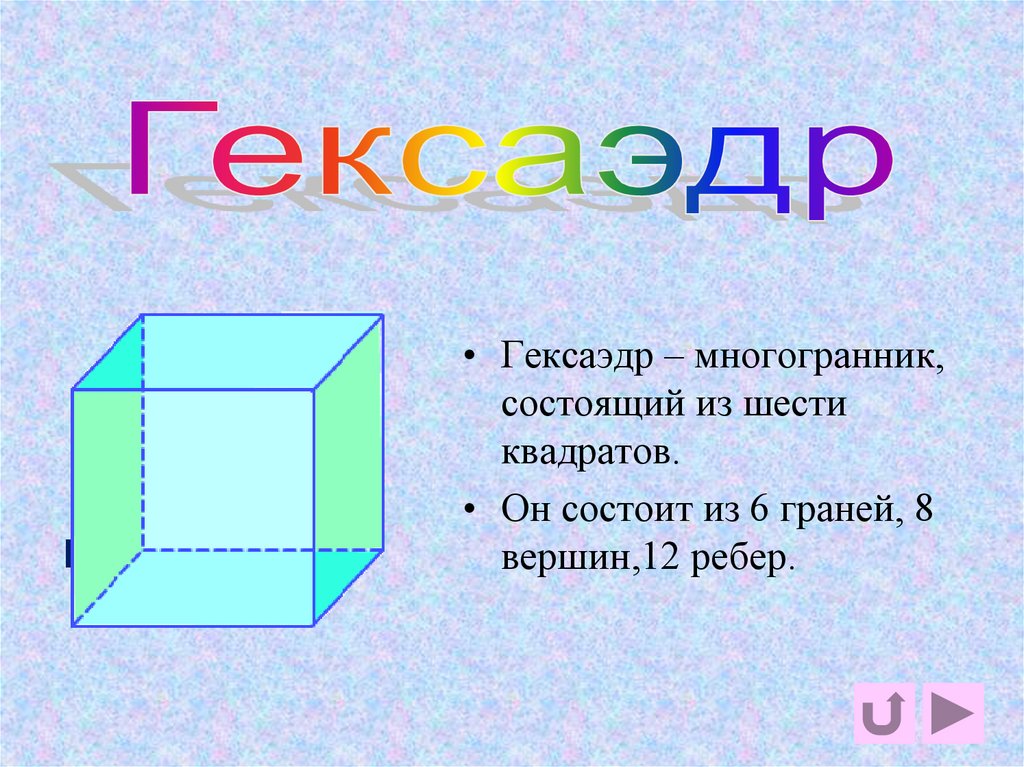
5. гексаэдр

• Гексаэдр – многогранник,
состоящий из шести
квадратов.
• Он состоит из 6 граней, 8
вершин,12 ребер.

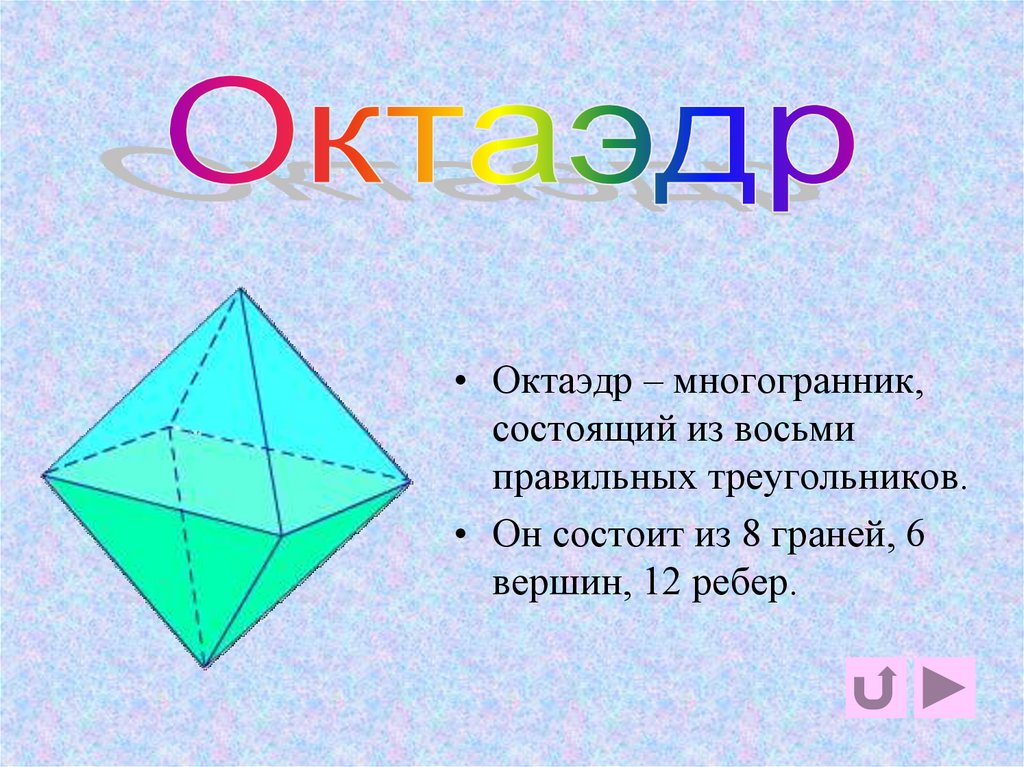
6. октаэдр

• Октаэдр – многогранник,
состоящий из восьми
правильных треугольников.
• Он состоит из 8 граней, 6
вершин, 12 ребер.

7. додекаэдр

• Додекаэдр – многогранник,
состоящий из двенадцати
правильных пятиугольников.
• Он имеет 12граней, 20
вершин, 30 ребер.

8. икосаэдр

• Икосаэдр - многогранник,
состоящий из двадцати
правильных треугольников.
• Он имеет 20 граней, 12
вершин, 30 ребер.

9.

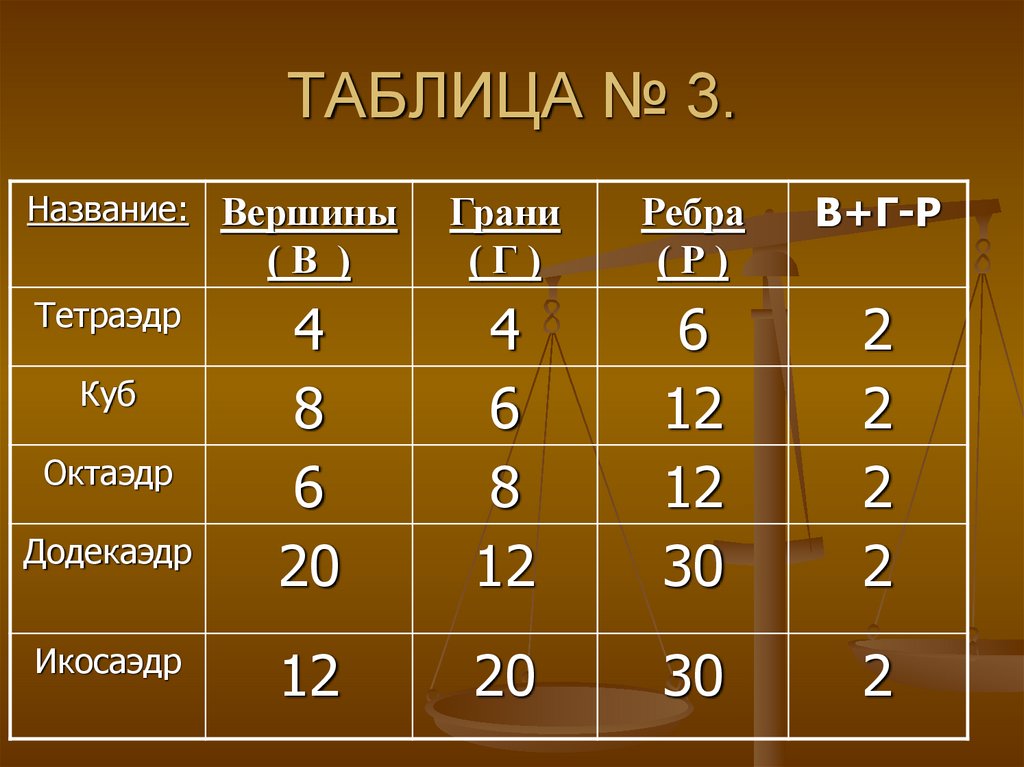
10. ТАБЛИЦА № 3.

Ребра
(Р)
В+Г-Р
(В )
Грани
(Г)
4
8
6
20
4
6
8
12
6
12
12
30
2
2
2
2
12
20
30
2
Название: Вершины
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр

11. Теорема Эйлера

Для любого выпуклого
многогранника
справедливо соотношение
Г+В-Р=2,
где
Г – число граней,
В – число вершин ,
Р – число ребер
данного многогранника.

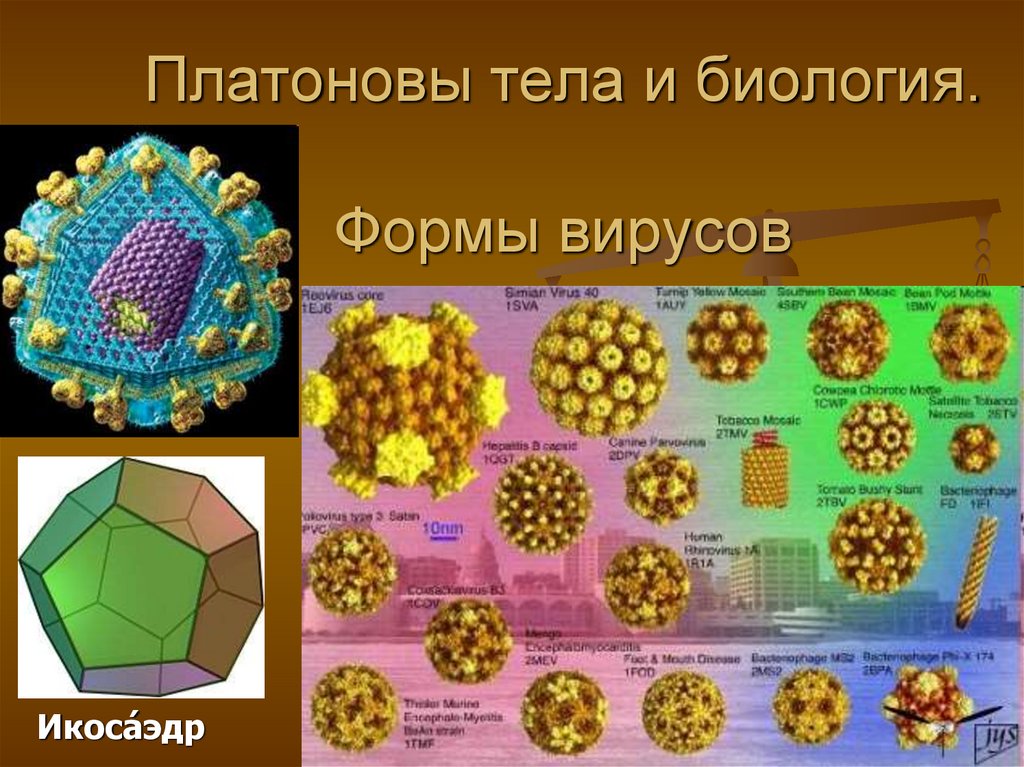
12. Платоновы тела и биология. Формы вирусов

Икоса́ эдр

13.

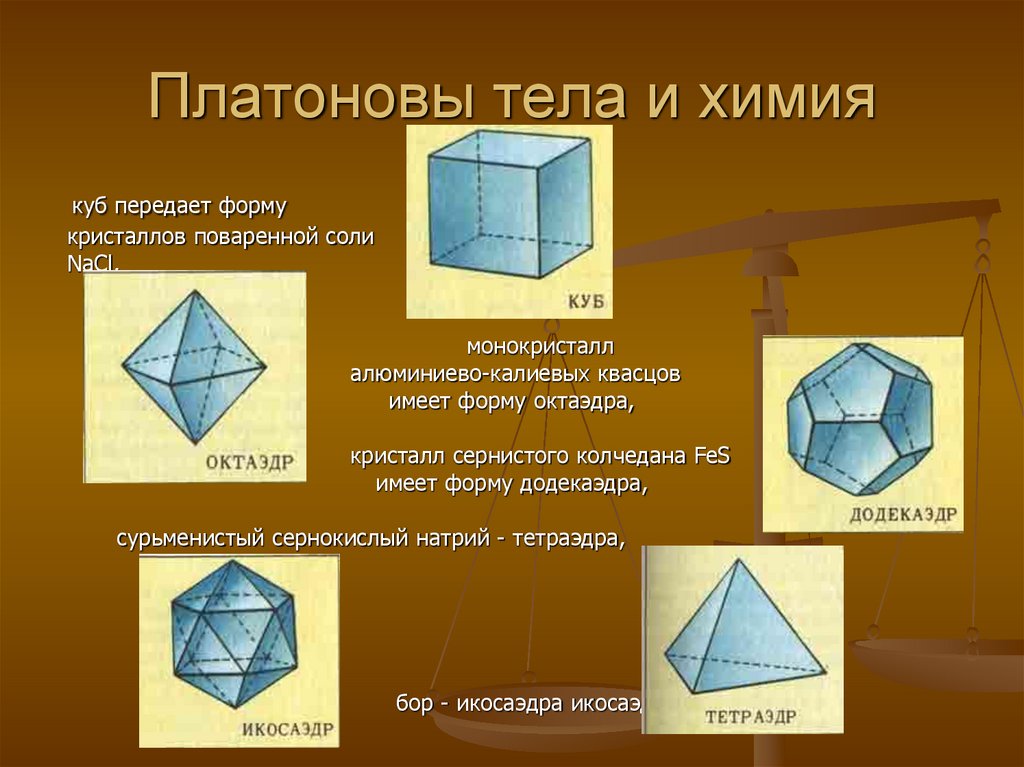
14. Платоновы тела и химия

куб передает форму
кристаллов поваренной соли
NaCl,
монокристалл
алюминиево-калиевых квасцов
имеет форму октаэдра,
кристалл сернистого колчедана FeS
имеет форму додекаэдра,
сурьменистый сернокислый натрий - тетраэдра,
бор - икосаэдра икосаэдра.

15. Архимедовы тела.

Архимедовыми телами
называются
полуправильные ,
однородные выпуклые многогранники ,
то есть выпуклые многогранники ,
все многогранные углы которых равны ,
а грани - правильные многогранники
нескольких типов
(этим они отличаются от платоновых тел,
грани которых - правильные многоугольники
одного типа).

16. Архимедовы тела.

(а)
(б)
усеченный усеченный
тетраэдр,
куб,
(в)
усеченный
октаэдр,
г)
(ж)
(д)
(е)
усеченный усеченныйкубооктаэдр,икосодо
декаэдр
додекаэдр, икосаэдр
.
(з)
ромбокубо
октаэдр,
(л)
курносый
додекаэдр
(и)
ромбоикосод
одекаэдр
(к)
курносый
куб
(м)
Ромбоусечеый
кубоктаэдр
(н)
Ромбоусеченй
икосододекаэдр
. Конструирование
Архимедовых тел

17.

Правильные
звездчатые многогранники
Кеплер первым
начал изучать
так называемые
звездчатые многогранники,
которые в отличие
от Платоновых и Архимедовых тел
являются правильными
невыпуклыми многогранниками.

18. Теория многогранников ( Платоновых тел) - одна из увлекательных и ярких разделов математики.

Теория многогранников ( Платоновых тел) одна из увлекательных и ярких разделов
математики.
В идеалистической картине мира, данной великим
мыслителем Платоном четыре из них олицетворяли
четыре стихии:
Тетраэдрогонь,
Кубземлю;
Икосаэдрводу;
Октаэдр –
воздух;
Додекаэдр –
символизировал все мироздание ,
по латыни его стали называть
«пятая сущность»

19.

Названия правильных многогранников пришли из Греции. В
дословном переводе с греческого "тетраэдр", "октаэдр", "гексаэдр",
"додекаэдр", "икосаэдр" означают: "четырехгранник",
"восьмигранник", "шестигранник". "двенадцатигранник",
"двадцатигранник". Этим красивым телам посвящена 13-я книга
"Начал" Евклида. Их еще называют телами Платона, т.к. они
занимали важное место в философской концепции Платона об
устройстве мироздания. Четыре многогранника олицетворяли в ней
четыре сущности или "стихии". Тетраэдр символизировал огонь, т.к.
его вершина устремлена вверх; икосаэдр - воду, т.к. он самый
"обтекаемый"; куб - землю, как самый "устойчивый"; октаэдр воздух, как самый "воздушный". Пятый многогранник, додекаэдр,
воплощал в себе "все сущее", символизировал все мироздание,
считался главным.

20. правильные многогранники

• Правильные многогранники - самые выгодные фигуры. И
природа этим широко пользуется. Кристаллы некоторых
знакомых нам веществ имеют форму правильных
многогранников. Так, куб передает форму кристаллов
поваренной соли NaCl, монокристалл алюминиево-калиевых
квасцов (KAlSO4)2 12Н2О имеет форму октаэдра, кристалл
сернистого колчедана FeS имеет форму додекаэдра,
сурьменистый сернокислый натрий - тетраэдра, бор - икосаэдра.
Правильные многогранники определяют форму кристаллических
решеток некоторых химических веществ.