Лекция_№_02_диэлектрики,_магнетики,_проводники,_резонансы

1. Лекция 2

Диэлектрики, проводники,
магнетики, резонансы

2. Проводники и диэлектрики

Проводники – вещества, в которых
сколь угодно малое электрическое
поле может вызывать перемещение
зарядов на сколь угодно большие
расстояния.
Диэлектрики – вещества, в которых
сколь угодно большое электрическое
поле может вызывать перемещение
зарядов только на расстояние,
сравнимое с размером молекулы.

3. Постоянный электрический ток

S
Электрический ток – упорядоченное движение заряженных частиц.
Сила тока
Плотность тока
dq
I
dt
dI
j
n
dS
I A
А
j 2
м

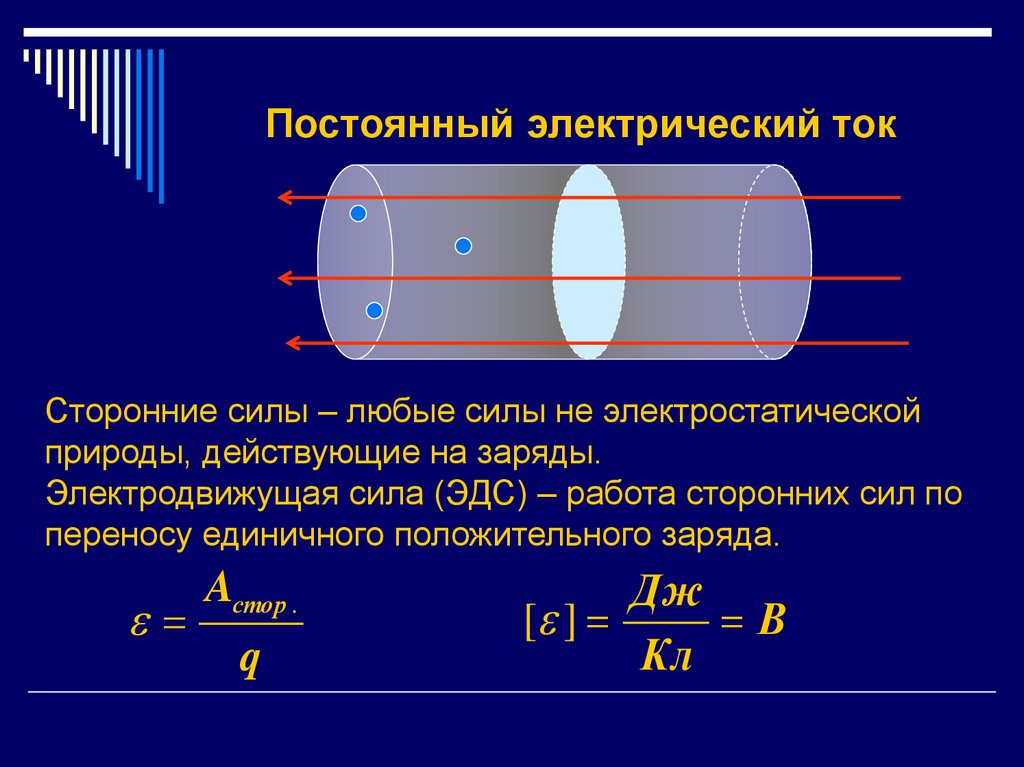
4. Постоянный электрический ток

Сторонние силы – любые силы не электростатической
природы, действующие на заряды.
Электродвижущая сила (ЭДС) – работа сторонних сил по
переносу единичного положительного заряда.
Aстор .
q
Дж
[ ]
В
Кл

5. Напряжение

– работа всех сил по переносу единичного
положительного заряда
U

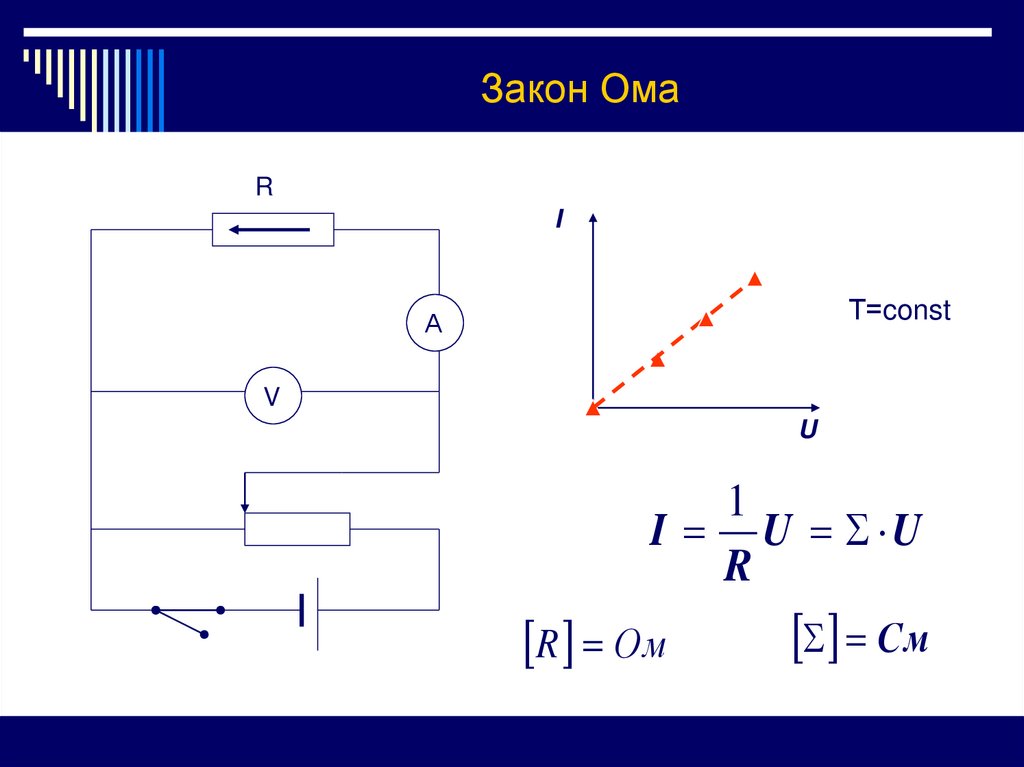
6. Закон Ома

R
I
I
1
U
R
А
R
l
S
Т=const
V
U
R
l
S
1
I U U
R
R Ом
Cм

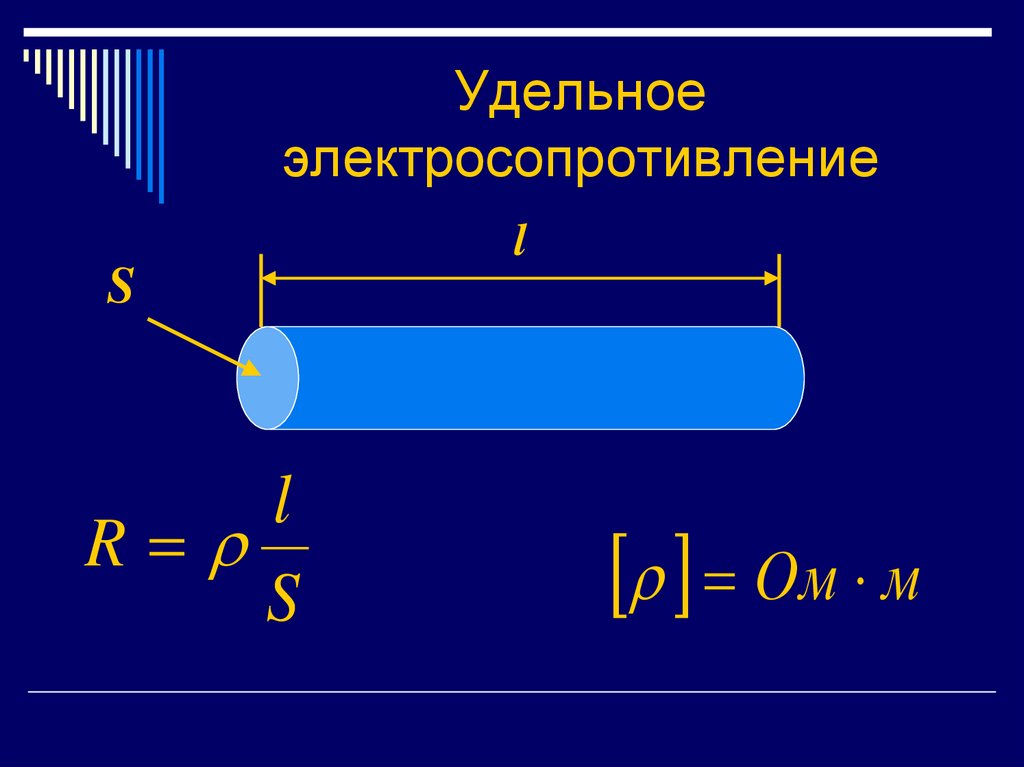
7. Удельное электросопротивление

l
S
l
R
S
Ом м

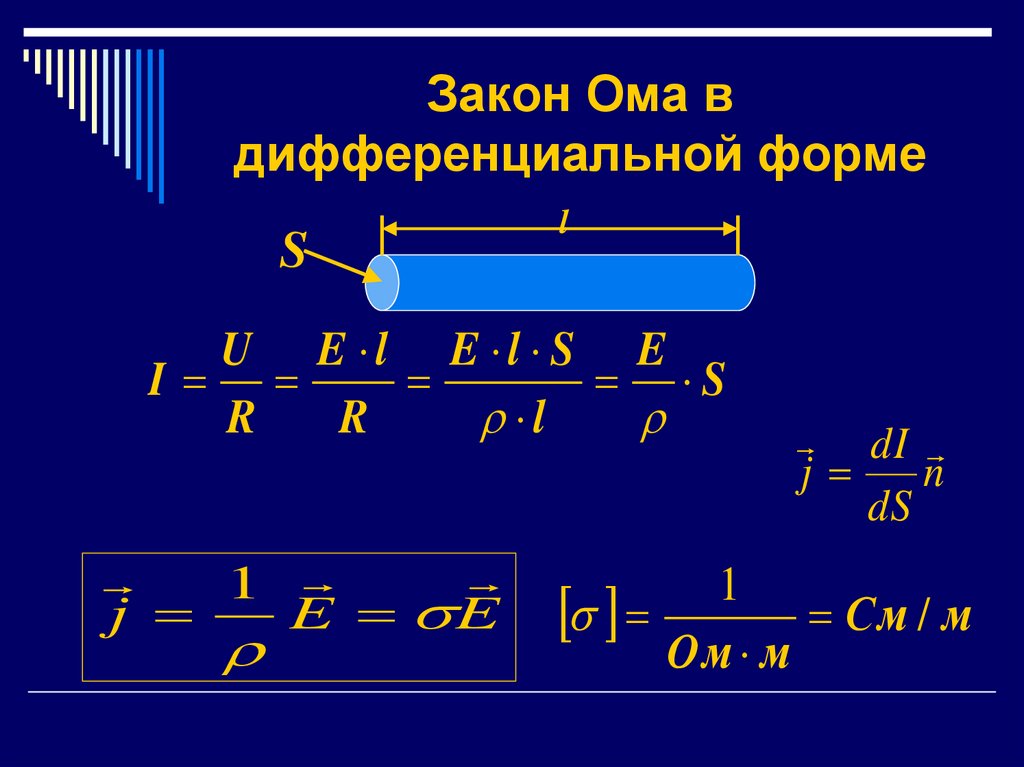
8. Закон Ома в дифференциальной форме

S
l
U E l E l S E
I
S
R
R
l
1
j
E E
dI
j
n
dS
1
См / м
Ом м

9. Закон Джоуля-Ленца

Интегральная форма
Работа тока
A q U I U t
Мощность тока
A
P I U
t
Тепло, выделяемое в проводнике
P I R
2
Q I Rt
2
Q
I R t j S l
Q уд
V t
V t
S S l
2
Дифференциальная форма
2
2
Q уд j E
2
2

10.

Lorentz
Hendrik
1853-1928
Drude
Paul Karl Ludwig
1863-1906
Основы классической
теории
электропроводности
металлов
(модель Друде – Лоренца,
1900 г.)

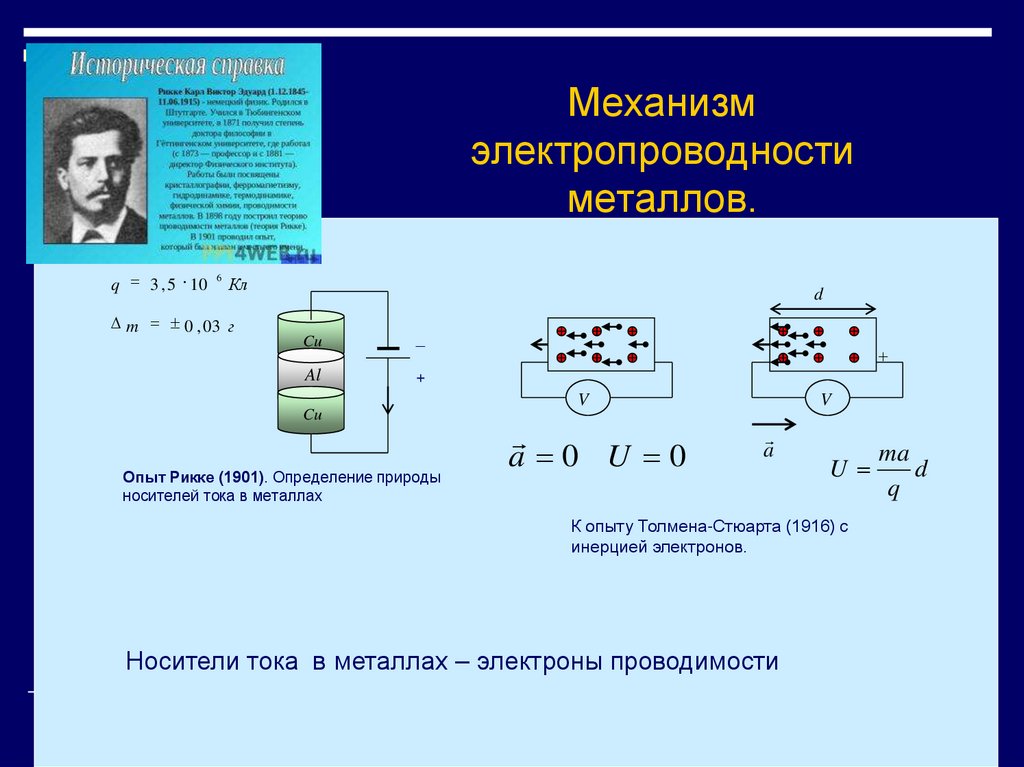
11. Механизм электропроводности металлов.

q 3 , 5 10
6
Кл
m 0 , 03 г
d
Cu
_
Al
+
Cu
Опыт Рикке (1901). Определение природы
носителей тока в металлах
_
V
a 0 U 0
V
a
U
К опыту Толмена-Стюарта (1916) с
инерцией электронов.
Носители тока в металлах – электроны проводимости
ma
d
q

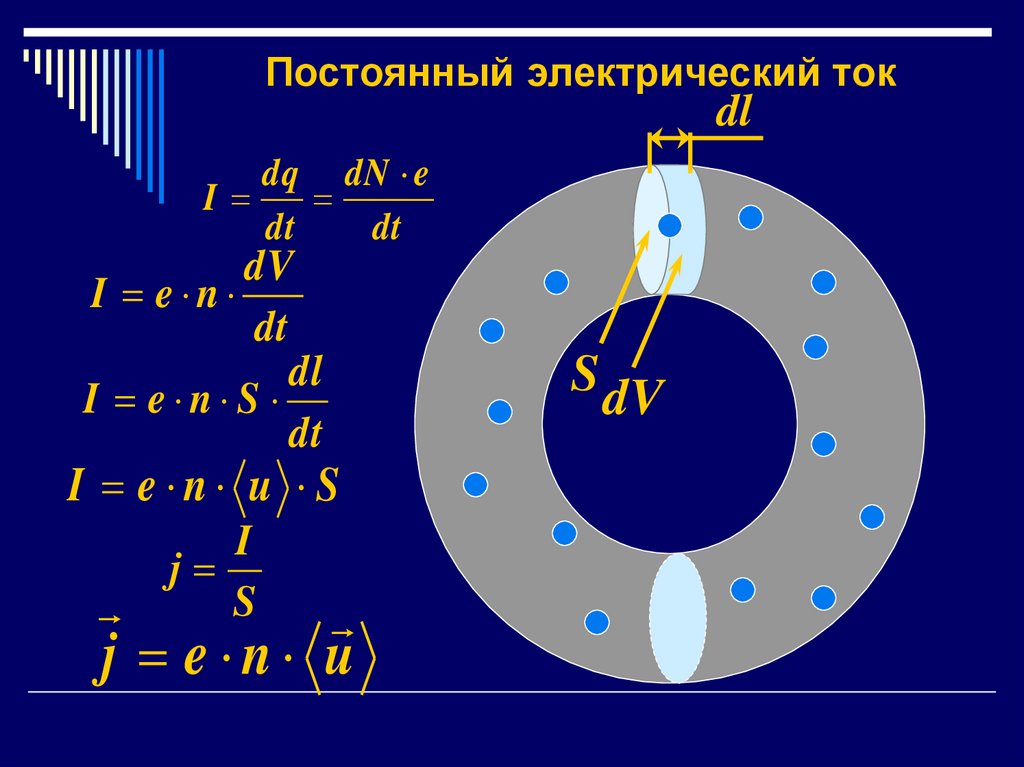
12. Постоянный электрический ток

dl
dq dN e
I
dt
dt
dV
I e n
dt
dl
I e n S
dt
I e n u S
I
j
S
j e n u
S dV

13. Оценка средней скорости кооперативного движения электронов проводимости

j e n u
n
N электронов
V
j
u
e n
N атомов z валентност ь m металла z плотность z N A
V
m атома V
8,9 10 3 1 6 10 23
29
3
nCu
0
,
8
10
м
63,5 10 3
u
А
jmax 10 2
м
10 7
3 м
10
19
29
1,6 10 0,8 10
с
7

14. Основные положения классической теории проводимости Друде –Лоренца.

Основные положения классической
теории проводимости Друде –
Лоренца.
1. Носители заряда – электроны, движение которых
подчиняется законам классической механики.
2. Можно не учитывать столкновения электронов
друг с другом. Взаимодействие с ионами – упругие
столкновения.
3. Поведение электронов подобно поведению
молекул идеального газа (электронный газ)
Средняя скорость хаотического движения электронов
8 kT
v
10 5 м / с
m
v u

15. Движение заряда в электрическом поле

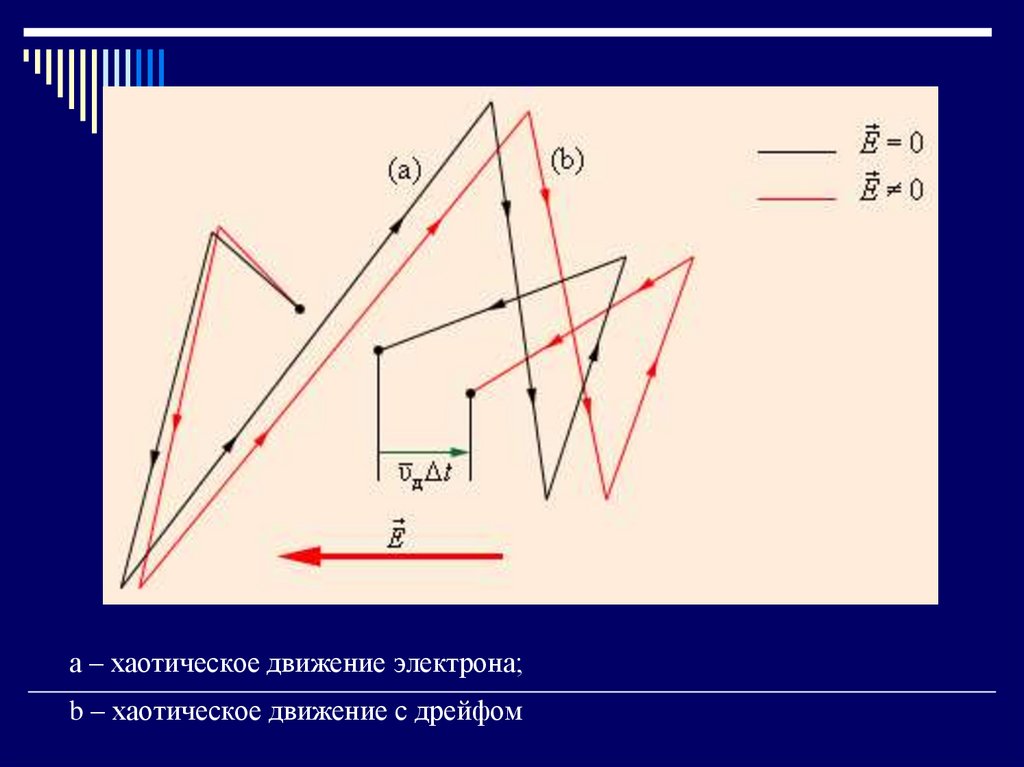
E

16. а – хаотическое движение электрона; b – хаотическое движение с дрейфом

а – хаотическое движение электрона;
b – хаотическое движение с дрейфом

17. Закон Ома в дифференциальной форме

_
eE
F m a eE a
m
v
j en u
j E
eE
umax a
m
eE
u
2m v
ne 2
2m v
Е
eE
u
2m
2m v
1/
ne 2

18. Закон Джоуля–Ленца в дифференциальной форме

Кинетическая энергия, передающаяся иону:
Общее число столкновений электронов
с ионами в единицу времени
me 2 2 E 2
2
mu max
W кин
2
N n
v
ne 2
2
Q уд E кин N
n
E
2
2m v
2m 2 v
Q уд Е
2
v
Q уд j
2

19. Длина свободного пробега

2m v
ne 2
плотность z N A
n
2m v
2
ne
2 m v
плотность z N A e 2
2 9,1 10 31 10 5 63,5 10 3
9
5
10
м
Медь: Cu
3
23
19 2
9
8,9 10 1 6 10 (1,6 10 ) 17 10

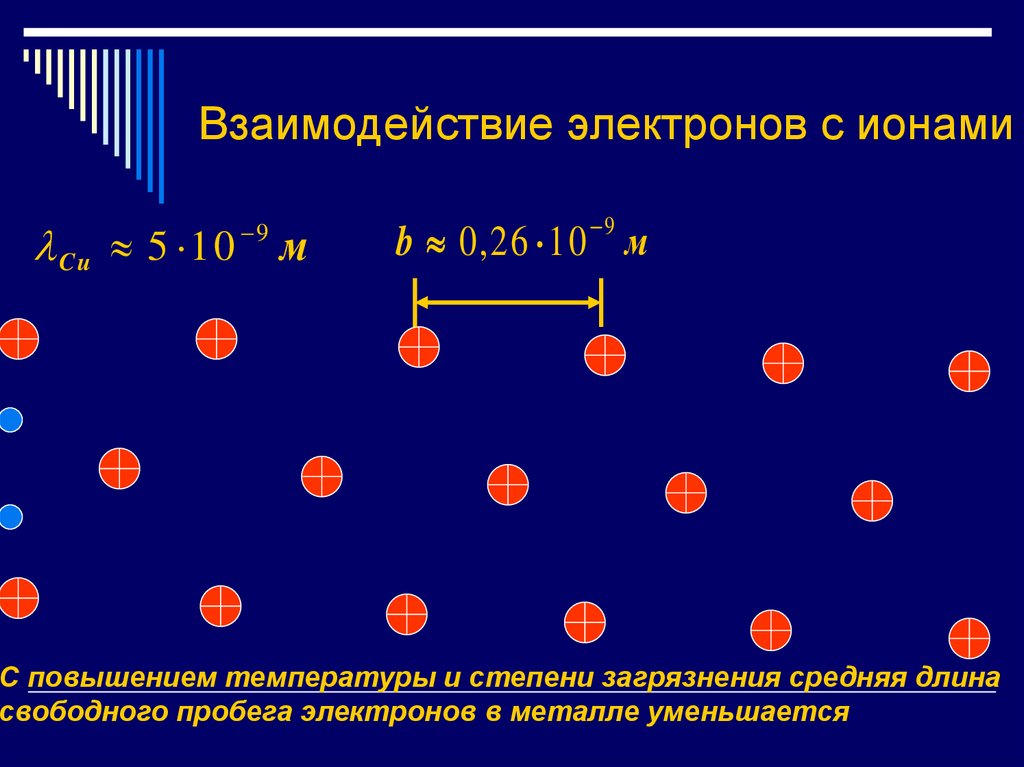
20. Взаимодействие электронов с ионами

Cu 5 10 м
9
9
b 0 , 26 10 м
С повышением температуры и степени загрязнения средняя длина
свободного пробега электронов в металле уменьшается

21.

22. Зависимость сопротивления металлов от температуры. Открытие сверхпроводимости (Г.Камерлинг-Онесс, 1911 г.)

1 - металл с примесями
2 - чистый металл или
интерметаллид
1
2
Тк
Т
Зависимость сопротивления металлов от температуры
в широком диапазоне температур вблизи Т= 300 К: R~T
Тк – температура
перехода в
сверхпроводящее
состояние
Вещество
Тк (К)
Титан
Алюминий
Ртуть
Свинец
0,4
1,2
4,1
7,2

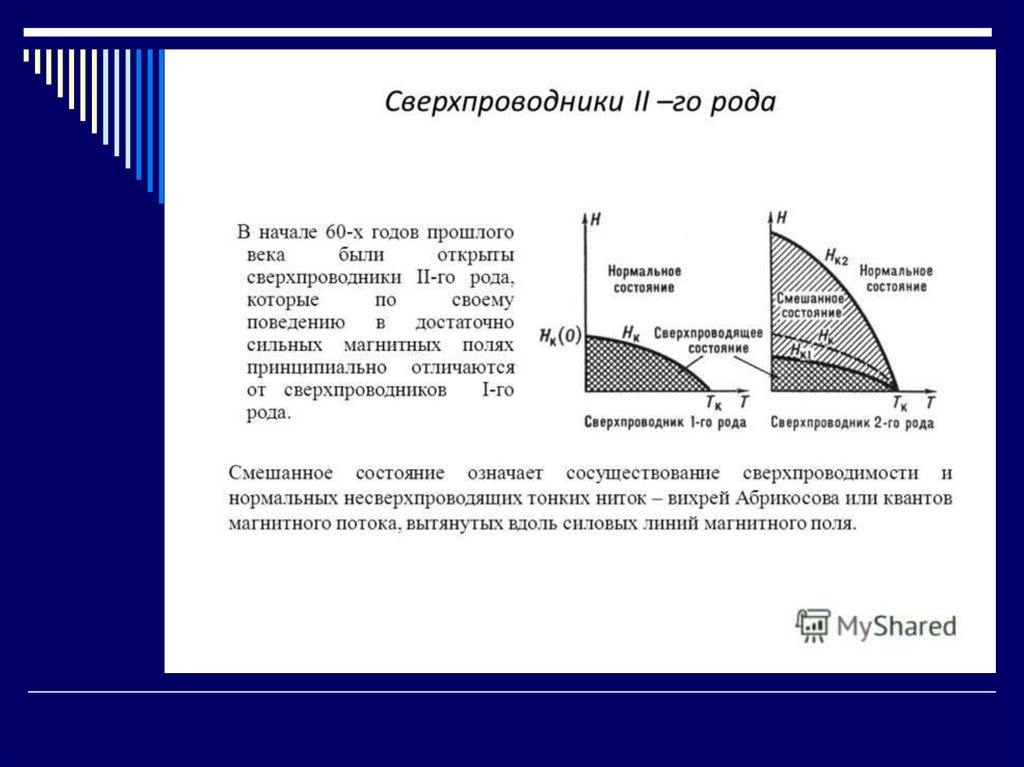
23. Высокотемпературная сверхпроводимость керамик

Высокотемпературная сверхпроводимость –
1986-1987 г.г.
Дж. Беднорц, К.А.Мюллер, М. Такашиге.
Металлоксиды (оксиды лантана, бария, др.
элементов)
YBa2Cu3O7-x
Температура перехода в сверхпроводящее
состояние ~ 100 К.

24. Сверхпроводящий провод

25.

26.

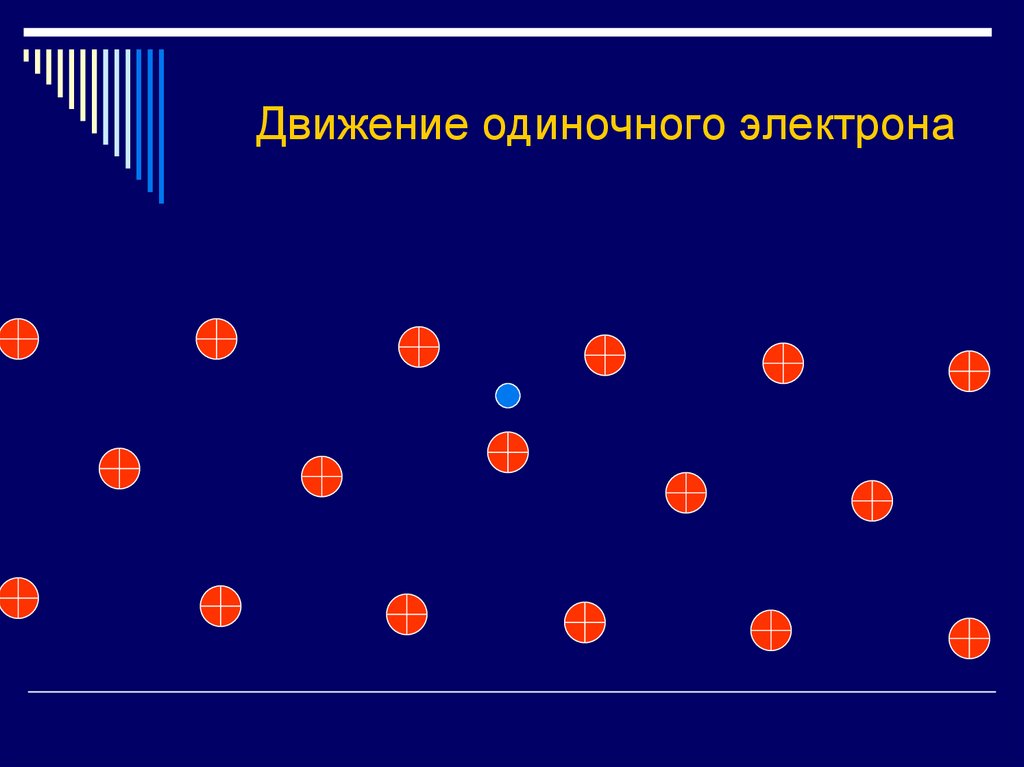
27. Движение одиночного электрона

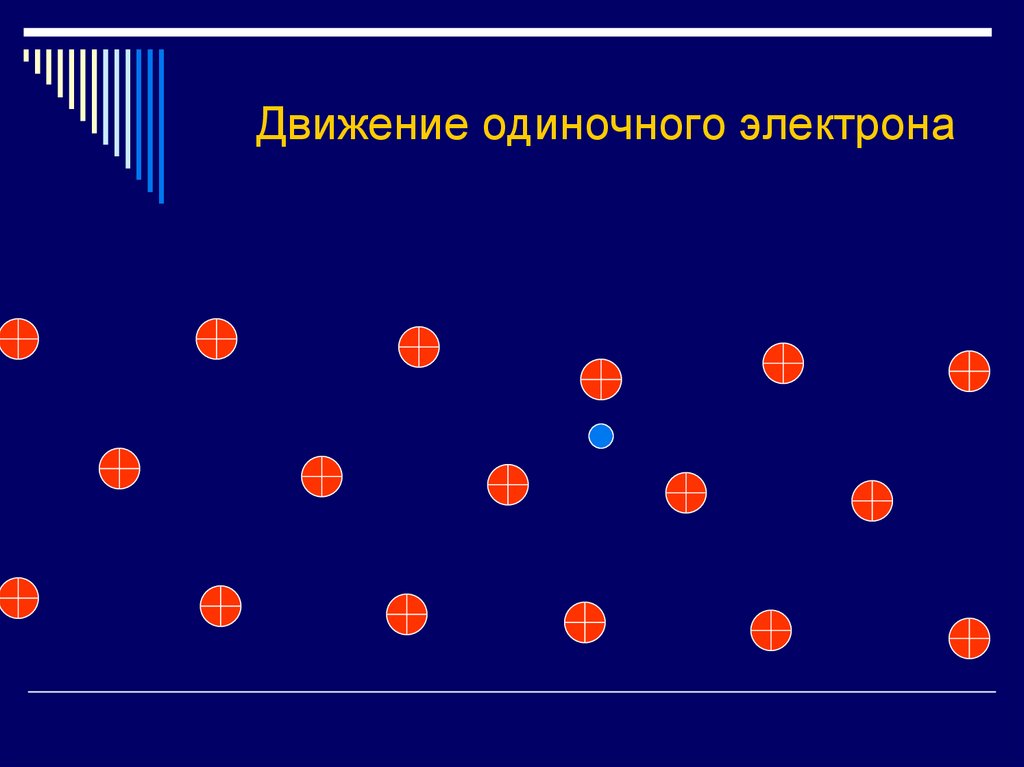
28. Движение одиночного электрона

29. Движение одиночного электрона

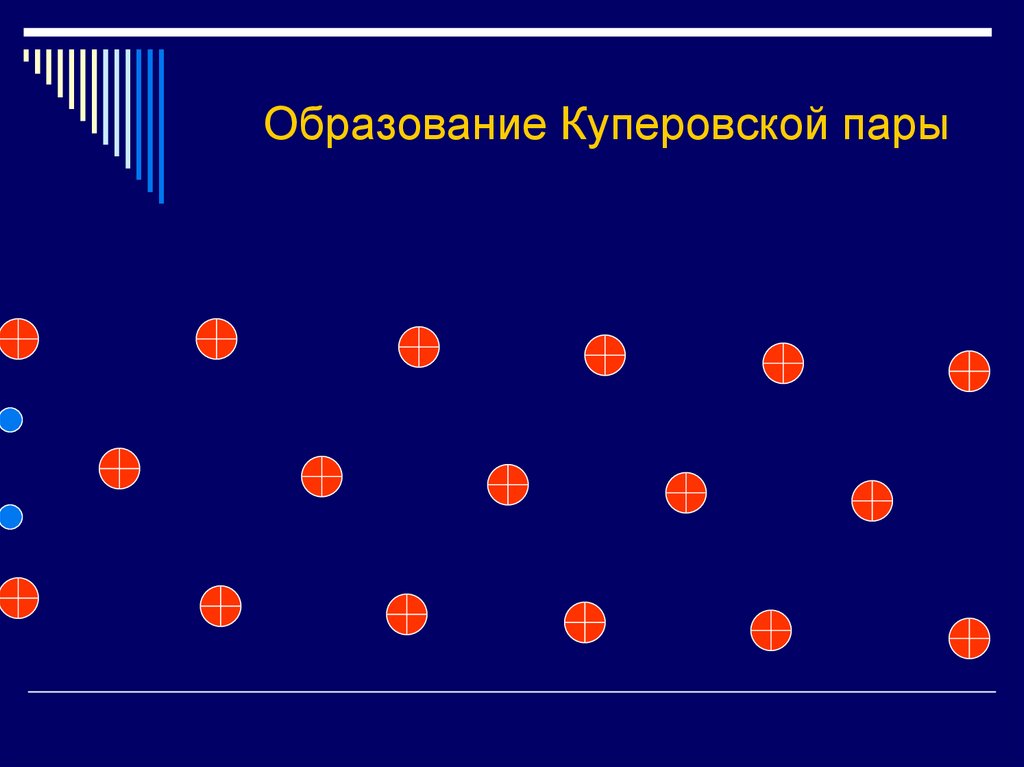
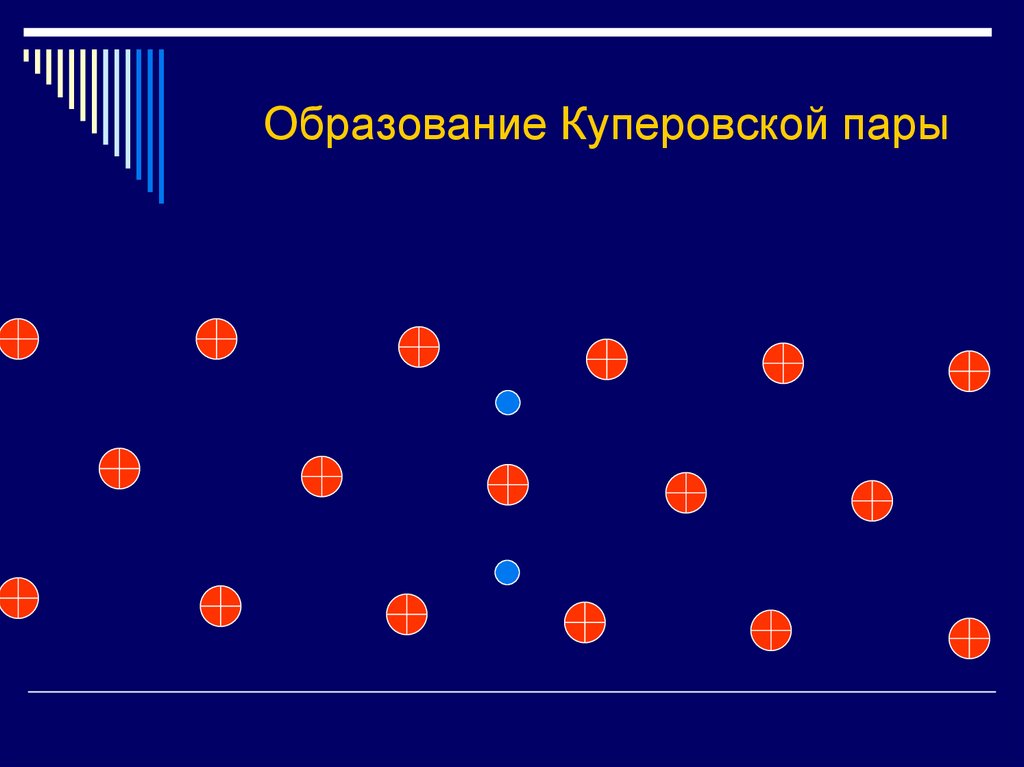
30. Образование Куперовской пары

31. Образование Куперовской пары

32. Электрический диполь

l r
Электрический диполь
r
+q
θ
l ~θ
-q
E
r
r
E
E E E
1 ql
2
E
3 1 3 cos
4 0 r
pe q l - электрический дипольный момент, Кл·м

33. Диполь во внешнем однородном электростатическом поле

pe
F q E
_
F q E
pe q l
E
F F F 0
N [ l ; F ]
2
l
N [
; F ]
2
N N N [l ; qE ] [ql ; E ]
N p e ; E N p e E sin

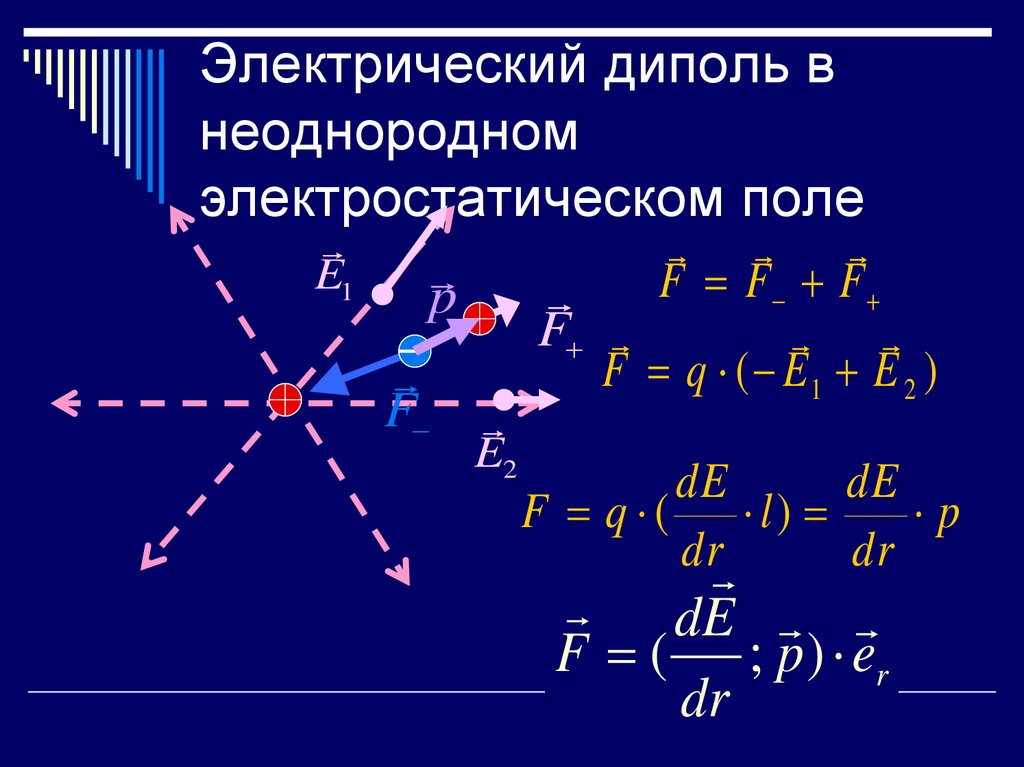
34. Электрический диполь в неоднородном электростатическом поле

E1
p
F
E2
F F F
F
F q ( E1 E 2 )
dE
dE
F q ( l)
p
dr
dr
dE
F ( ; p ) er
dr

35. Энергия диполя во внешнем электрическом поле

dE
F ( ; p ) er
dr
We Fdr E p
Энергия диполя минимальна при
E p
- устойчивое равновесие

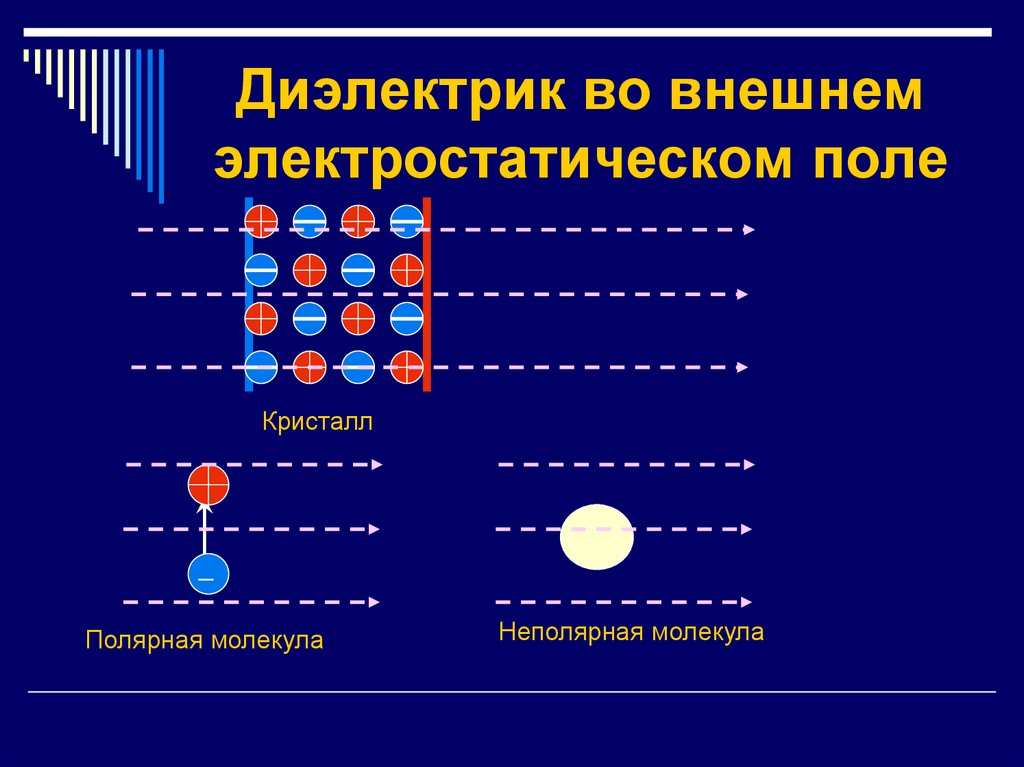
36. Диэлектрик во внешнем электростатическом поле

Кристалл
_
_
Полярная молекула
Неполярная молекула

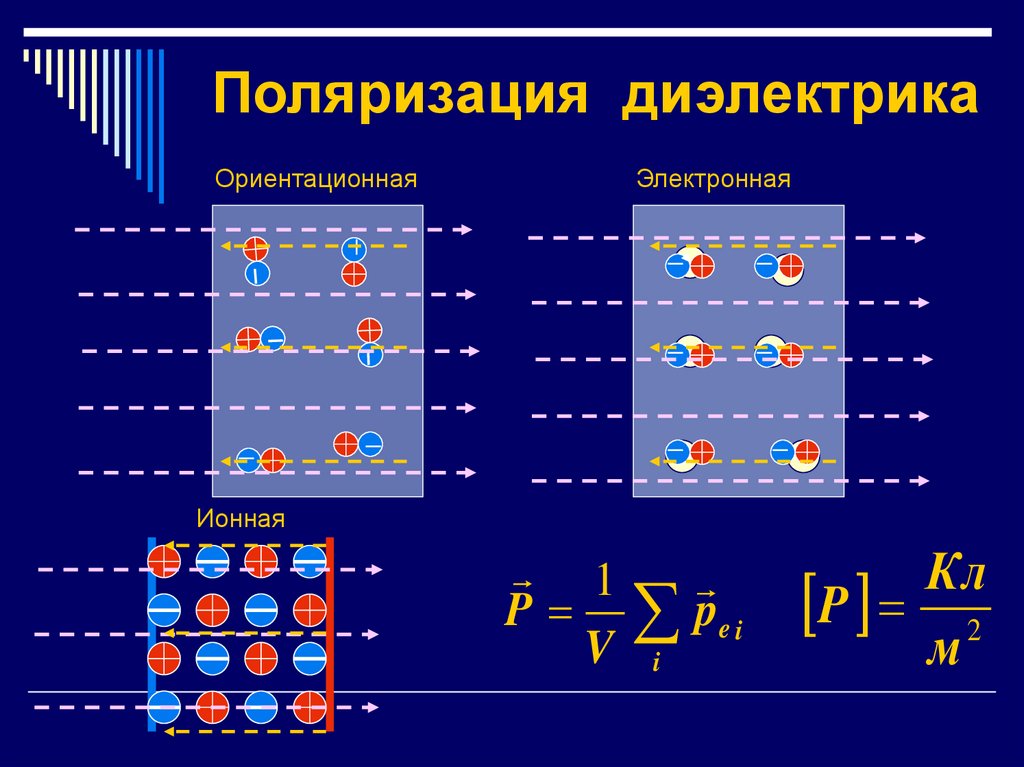
37. Поляризация диэлектрика

Ориентационная
_
_
_
Электронная
_
_
_
_
_
_
Ионная
1
P pe i
V i
Кл
P 2
м

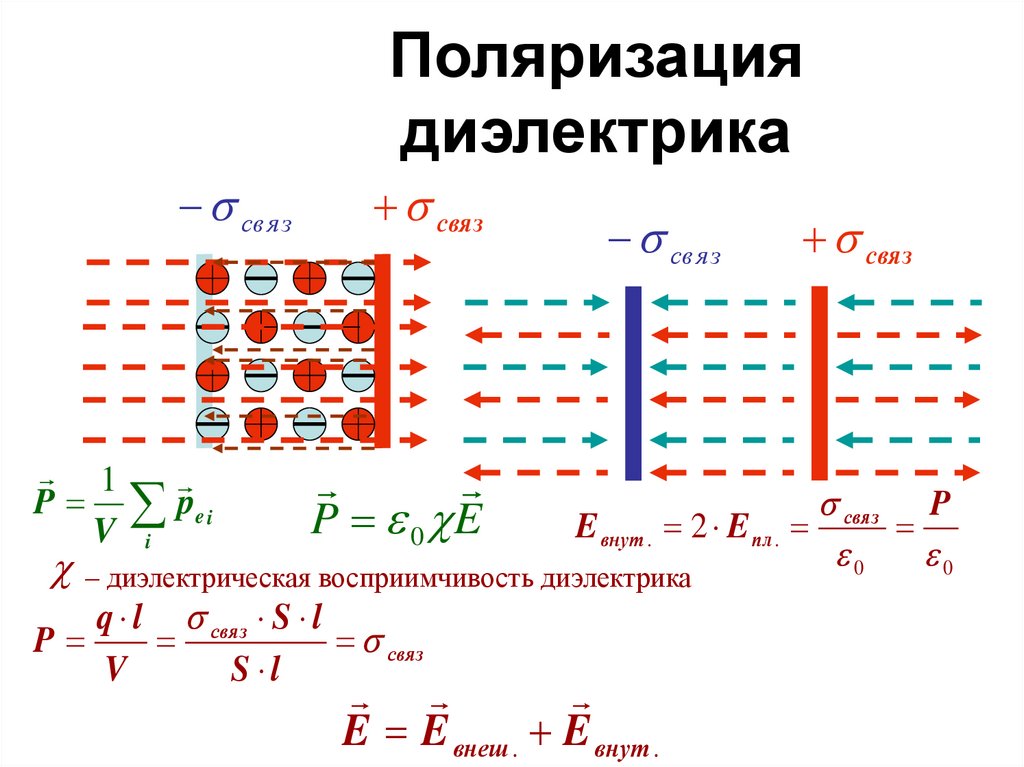
38. Поляризация диэлектрика

связ
1
P pe i
V i
св я з
P 0 E
связ
связ P
E внут . 2 E пл .
0
0
– диэлектрическая восприимчивость диэлектрика
q l связ S l
P
связ
V
S l
связ
E E внеш . E внут .

39. Поляризация диэлектрика

E E внеш . E внут .
E E внеш . E внут .
P
E внут .
0
P 0 E
P
E внеш . E E E (1 ) E
0
1
– диэлектрическая проницаемость
E внеш . E

40. Поле внутри диэлектрика уменьшается в ε раз

1
q
E точечного _ заряда
2
4 0 r
E нити
2 0 r
E плоскости
2 0
q
Ф E E dS
0
S
div ( E )
0

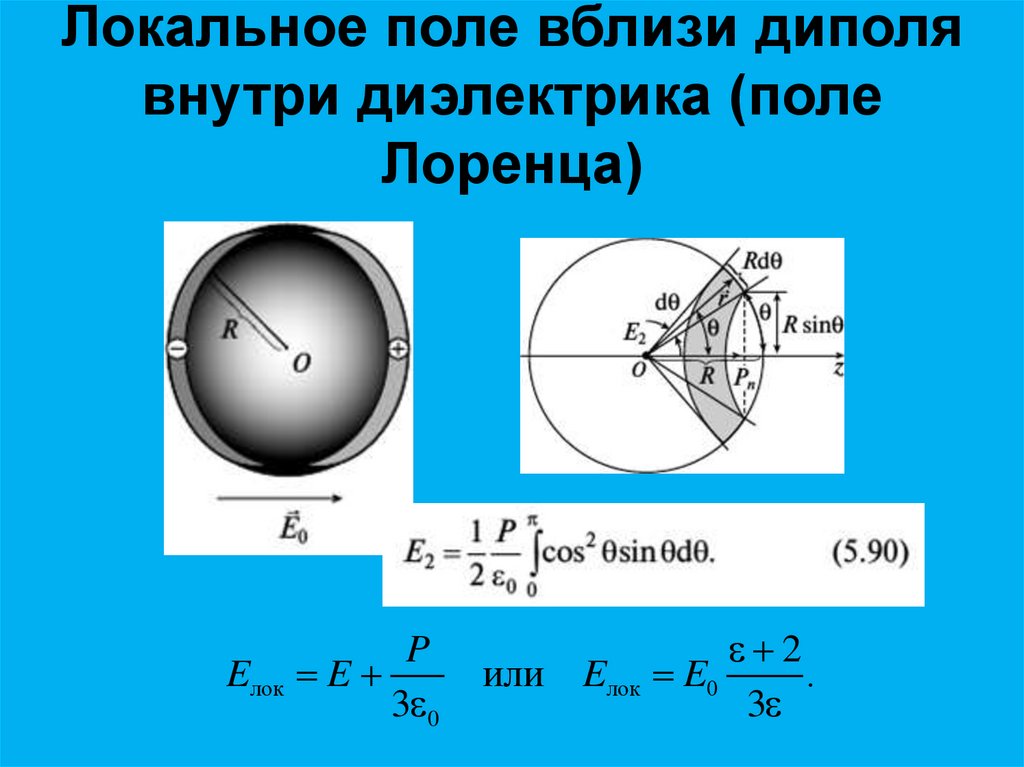
41. Локальное поле вблизи диполя внутри диэлектрика (поле Лоренца)

P
Eлок E
3 0
2
или Eлок E0
.
3

42. Поляризуемость молекул диэлектрика

р = αε0Елок
α – поляризуемость молекулы
n
,
3
3
1
n
или
2
3
M 1
N A – уравнение
.
2
3 Мосотти-Клаузиуса

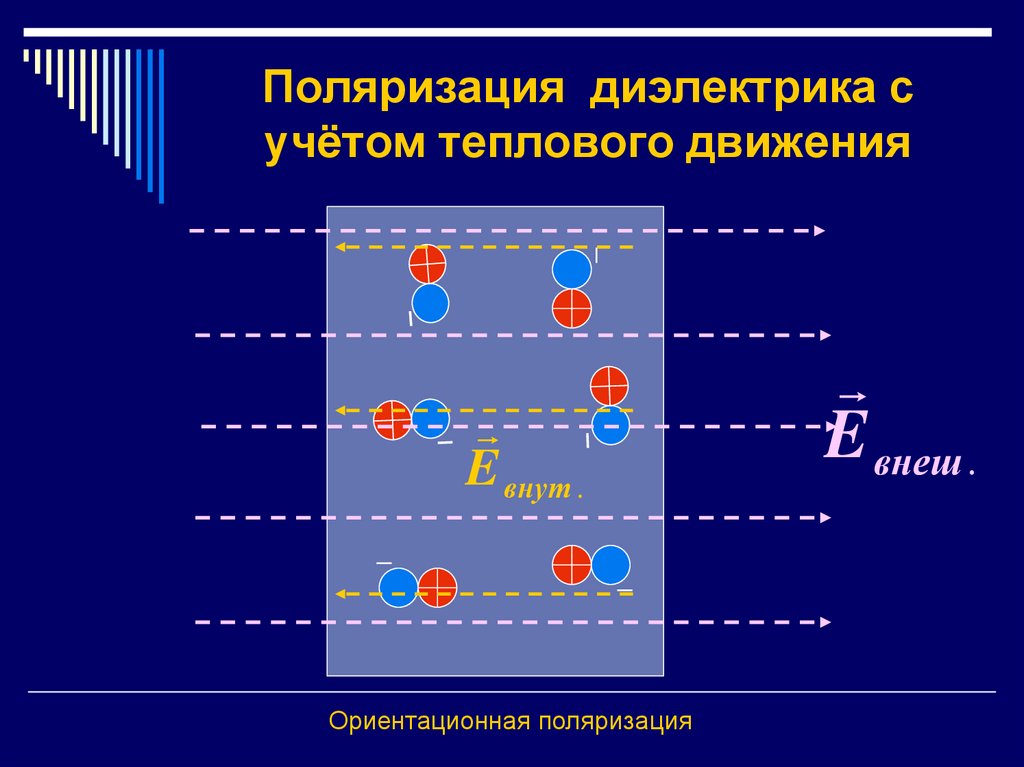
43. Поляризация диэлектрика с учётом теплового движения

_
E внеш .
E внут .
_
_
Ориентационная поляризация

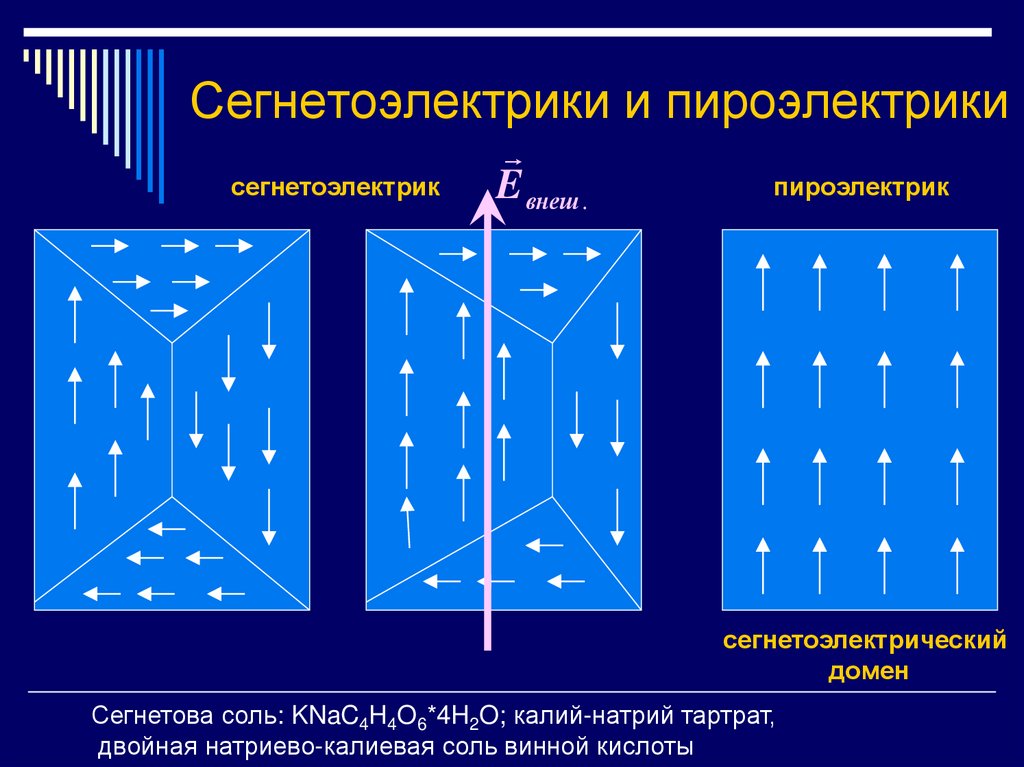
44. Сегнетоэлектрики и пироэлектрики

сегнетоэлектрик
E внеш .
пироэлектрик
сегнетоэлектрический
домен
Сегнетова соль: KNaC4H4O6*4H2O; калий-натрий тартрат,
двойная натриево-калиевая соль винной кислоты

45. Электрическое смещение

E E
E
0 E D P
внеш .
внут .
P
E внут .
0
0 E 0 E внеш . P
D 0 E внеш .
P 0 E
D 0 (1 ) E 0 E
Кл
D 2
м

46. Поле внутри диэлектрика уменьшается в ε раз

1
q
E точечного _ заряда
2
4 0 r
E нити
2 0 r
E плоскости
2 0
q
Ф E E dS
0
S
D 0 E
1 q
D
2
4 r

47.

Стрикция,
пьезоэлектричество

48. Поляризация диэлектрика

св яз
1
P pe i
V i
связ
P 0 E
св яз
связ P
E внут . 2 E пл .
0
0
– диэлектрическая восприимчивость диэлектрика
q l связ S l
P
связ
V
S l
связ
E E внеш . E внут .

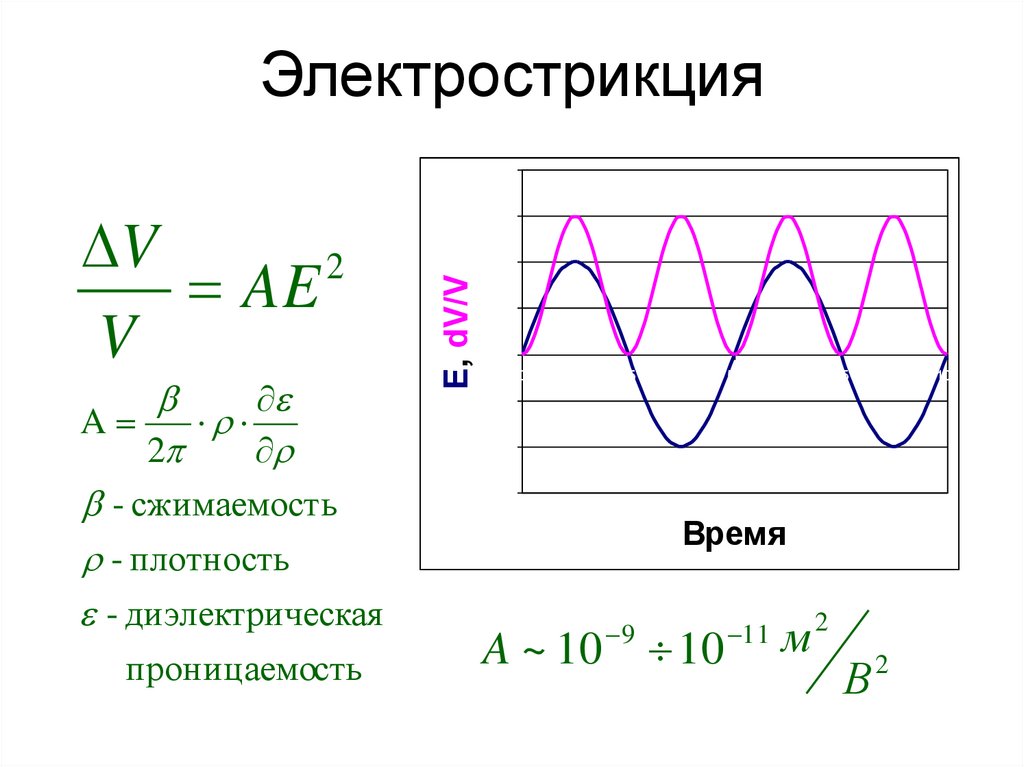
49. Электрострикция

2
A
2
- сжимаемость
- плотность
- диэлектрическая
проницаемость
1
E, dV/V
V
2
AE
V
1,5
0,5
0
0
25
50
75
-0,5
-1
-1,5
Время
9
A ~ 10 10
11
м
2
В2
100

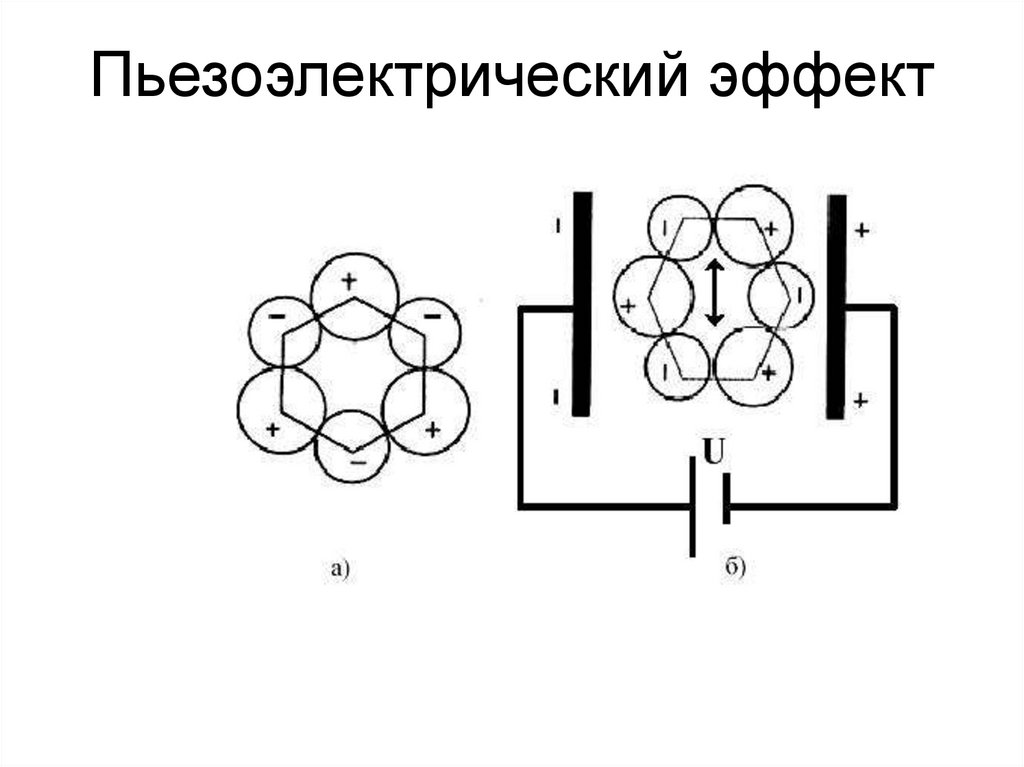
50. Пьезоэлектрический эффект

51. Пьезоэлектрический эффект

• возникновение электрической поляризации в
веществе в отсутствие электрического поля при
упругих деформациях (прямой
пьезоэлектрический эффект) и появление
механических деформаций под действием
электрического поля (обратный
пьезоэлектрический эффект).
• Первое исследование пьезоэлектрического
эффекта осуществлено братьями Пьером и
Жаном Кюри (1880) на кристалле кварца.
• Пьезоэлектрический эффект обнаружен более
чем у 1500 веществ. Пьезоэлектрический
эффект наблюдается у всех сегнетоэлектриков и
у многих пироэлектриков.

52. Пьезоэлектрический эффект

• В общем виде уравнение
прямого пьезоэффекта при
воздействии однородного
механического напряжения σ
записывается так:
• Где Pi - компонент вектора
поляризации; dir - пьезомодуль;
σr - компонент механического
напряжения.
• Уравнение обратного
пьезоэффекта записывается так:
• Где δi - компонент упругой
деформации; Er - компонент
напряжённости электрического
поля.
3
Pi ( d ir r )
r 1
3
i ( Dir E r )
r 1

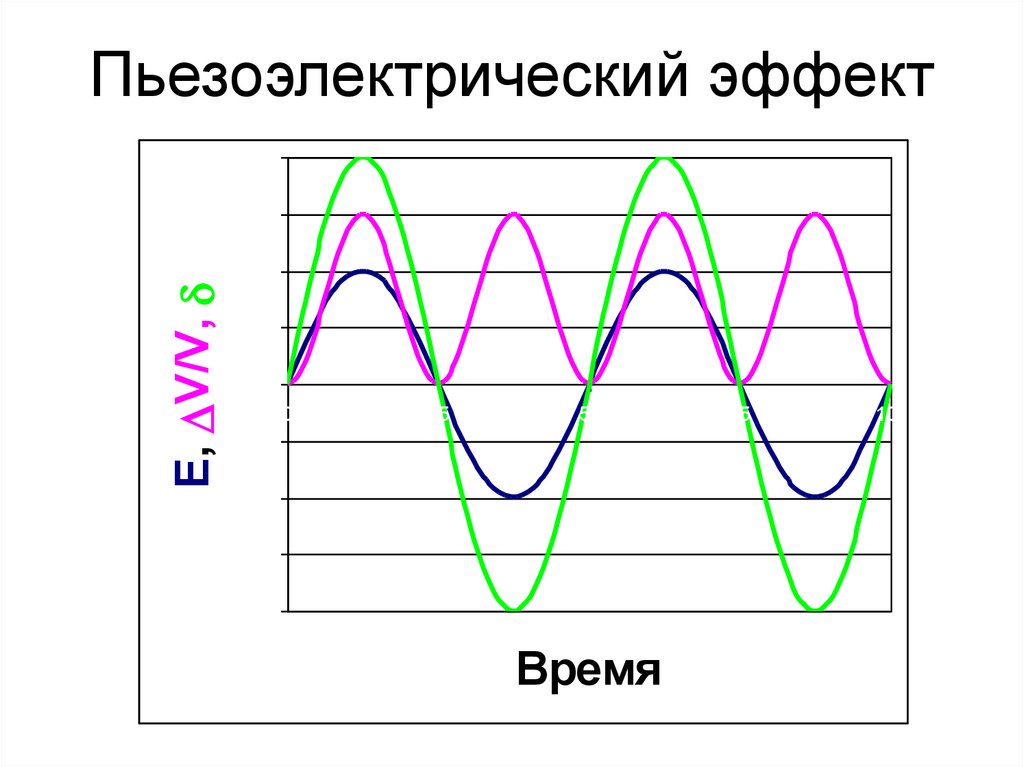
53. Пьезоэлектрический эффект

2
E, V/V,
1,5
1
0,5
0
0
25
50
-0,5
-1
-1,5
-2
Время
75
100

54. Лекция 7

Магнитные
свойства вещества

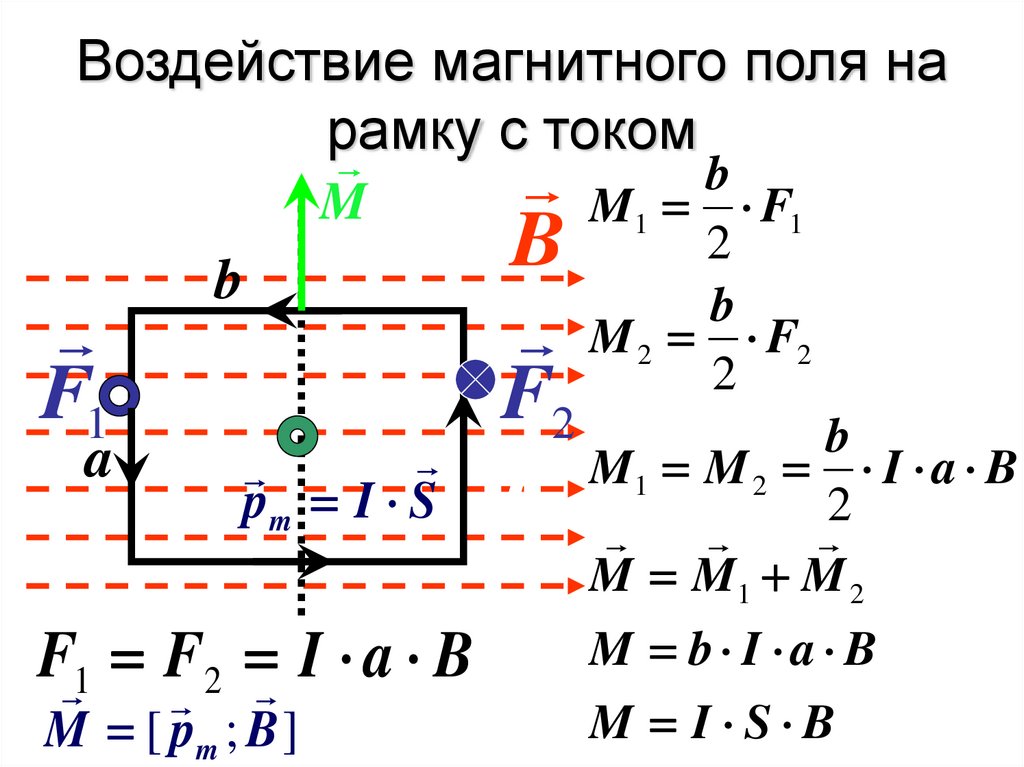
55. Воздействие магнитного поля на рамку с током

M
F1
a
b
pm I S
M b F
2
B
b
M 2 F
F2
b
M M I a B
I 2
1
1
2
2
1
2
M M1 M 2
F 1 F2 I a B
M [ pm ; B ]
M b I a B
M I S B

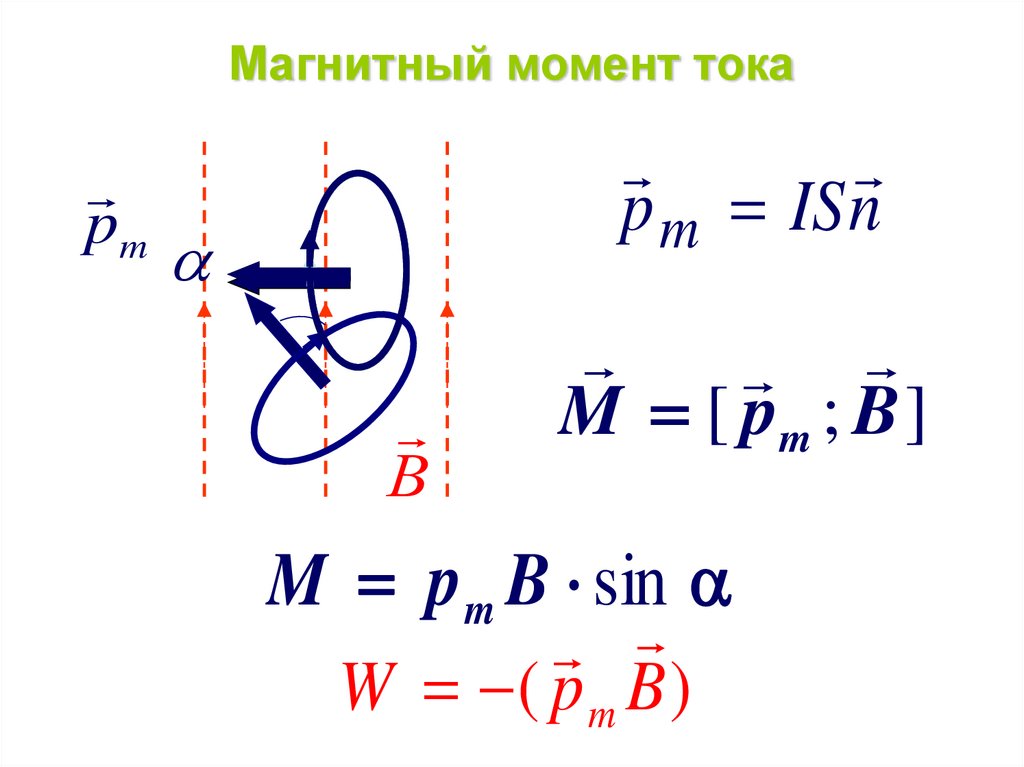
56. Магнитный момент тока

pm
p m IS n
В
M [ pm ; B ]
M p m B sin
W ( p m B )

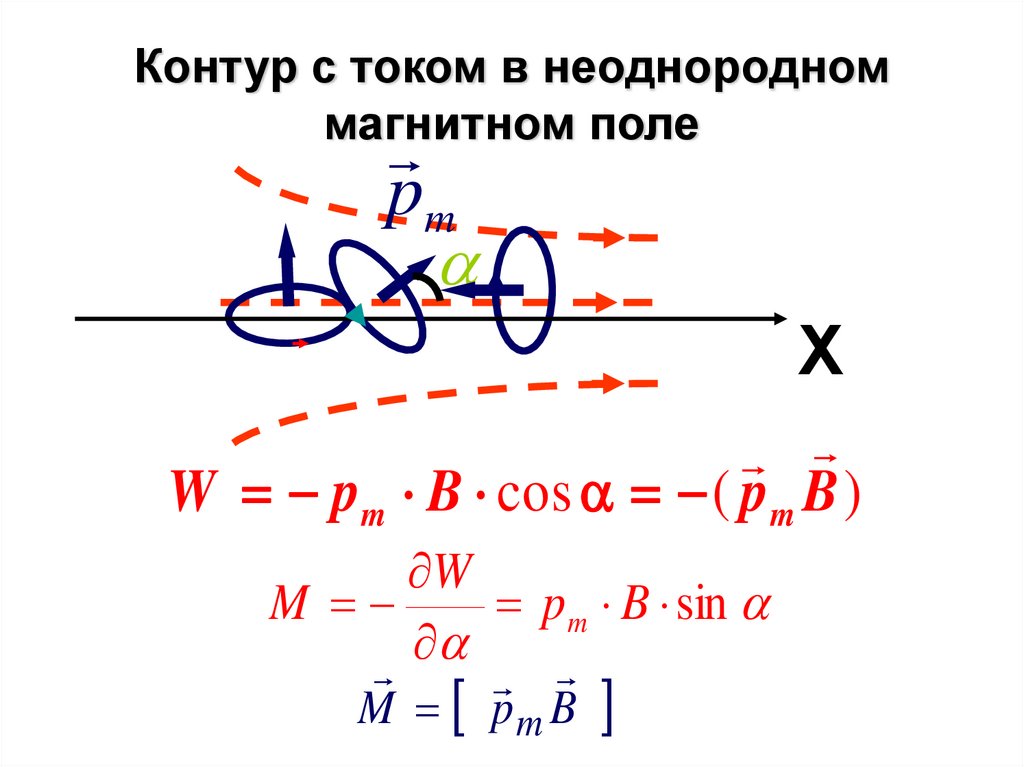
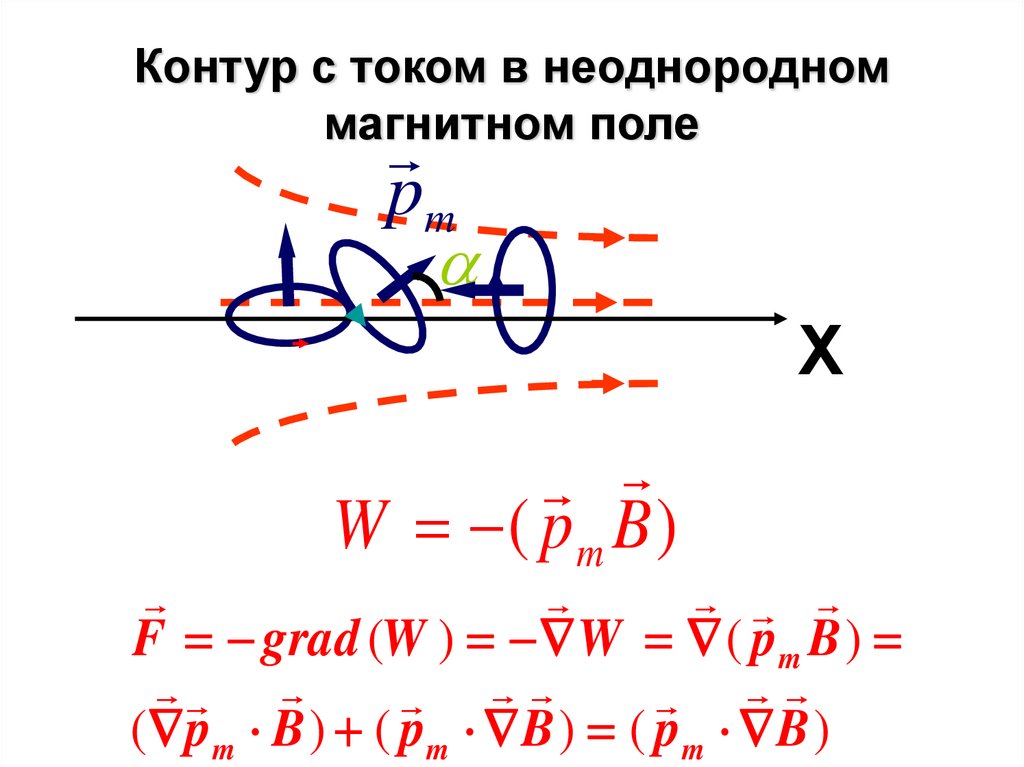
57. Контур с током в неоднородном магнитном поле

pm
Х
W pm B cos ( pm B )
W
M
p m B sin
M pm B

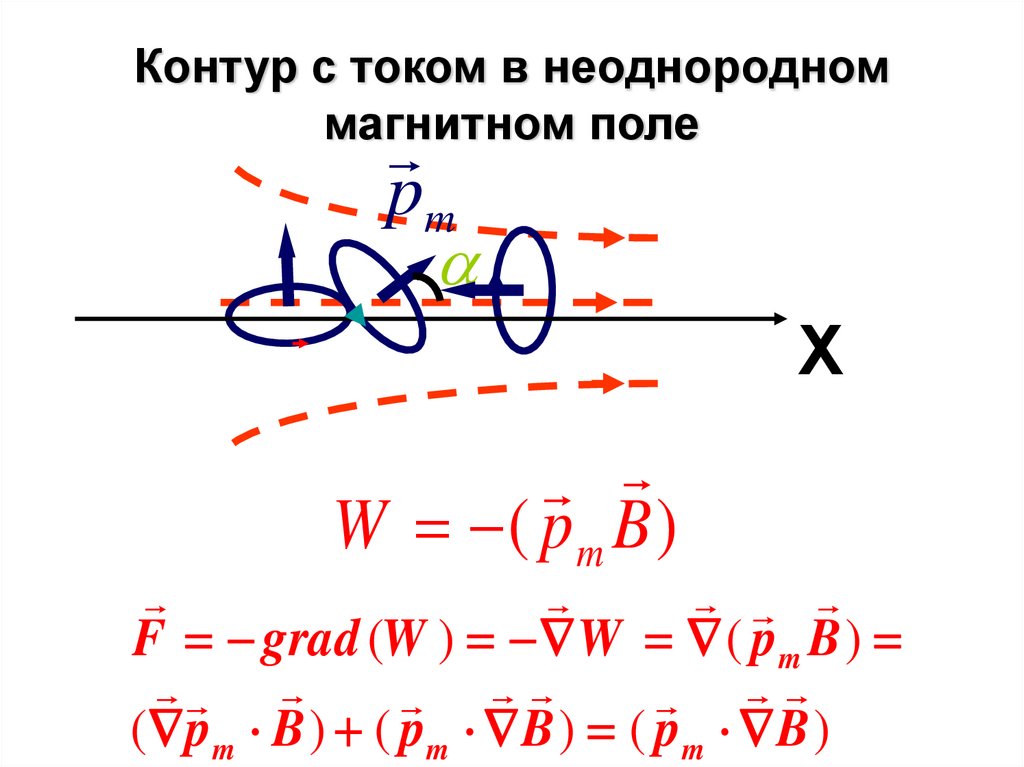
58. Контур с током в неоднородном магнитном поле

pm
Х
W ( pm B )
F grad (W ) W ( pm B )
( p m B ) ( p m B ) ( p m B )

59. Контур с током в неоднородном магнитном поле

pm
Х
W ( pm B )
F grad (W ) W ( pm B )
( p m B ) ( p m B ) ( p m B )

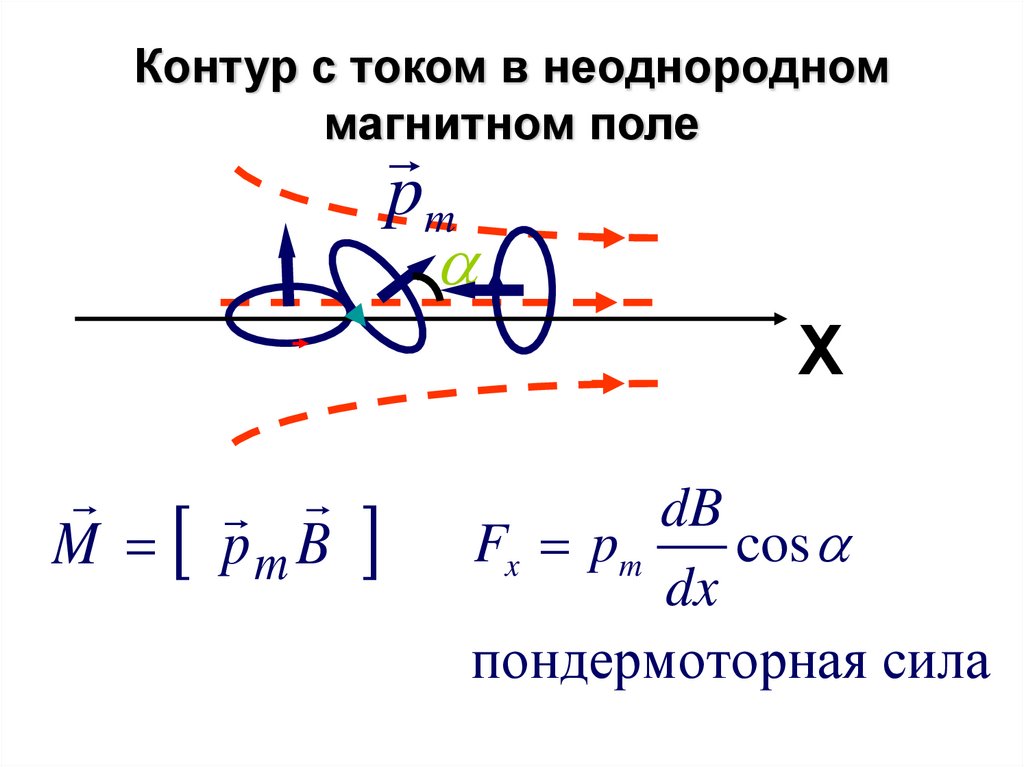
60. Контур с током в неоднородном магнитном поле

pm
Х
M pm B
dB
Fx pm
cos
dx
пондермоторная сила

61. Гипотеза Ампера. Молекулярные токи.

B0 0
pmi 0
i
B' 0
B0 0
pmi 0
i
B' 0
А м2 А
J 3
м
м
В0
В'
B B0 B
Вектор намагниченности
1
B'
J
pmi
V
0

62. Вычисление поля в магнетиках

Вектор намагниченности
1
B'
J
pmi
V
0
B0 B B '
Напряженность
магнитного поля H
0
0
B
А
H
J
[H ]
0
м
J H
B
H H
0
B
H
0 (1 )
1
магн и тн ая п рон и ц аемость веществ а
магн и тн ая восп ри и мчивость веществ а

63. Магнитная проницаемость

• B= µ0 µ H
• µ=B/B0

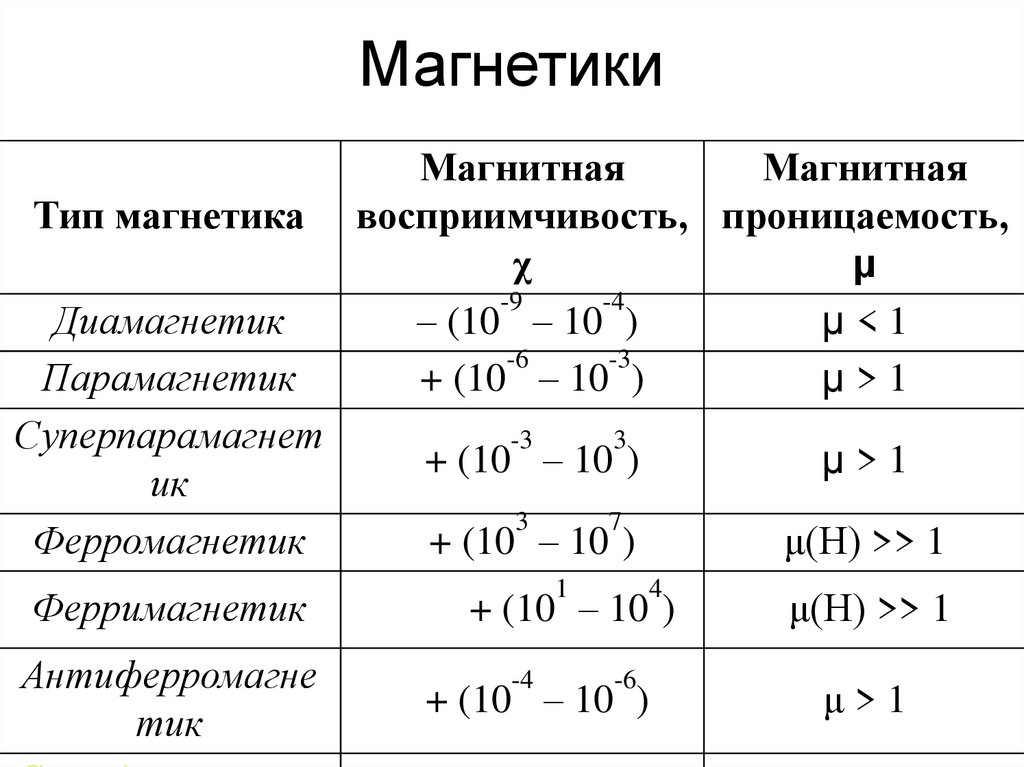
64. Магнетики

Тип магнетика
Диамагнетик
Парамагнетик
Суперпарамагнет
ик
Ферромагнетик
Ферримагнетик
Антиферромагне
тик
Магнитная
Магнитная
восприимчивость, проницаемость,
χ
μ
-9
-4
– (10 – 10 )
μ<1
-6
-3
+ (10 – 10 )
μ>1
-3
3
+ (10 – 10 )
μ>1
3
7
μ(Н) >> 1
+ (10 – 10 )
1
4
+ (10 – 10 )
-4
-6
+ (10 – 10 )
μ(Н) >> 1
μ>1

65. Природа парамагнетизма

B0 0
pmi 0
i
B' 0
B0 0
pmi 0
В'
В0
B B0 B 0 ( H J )
i
B' 0
Закон Кюри :
C
χ
T

66. Перемагничивание парамагнетиков

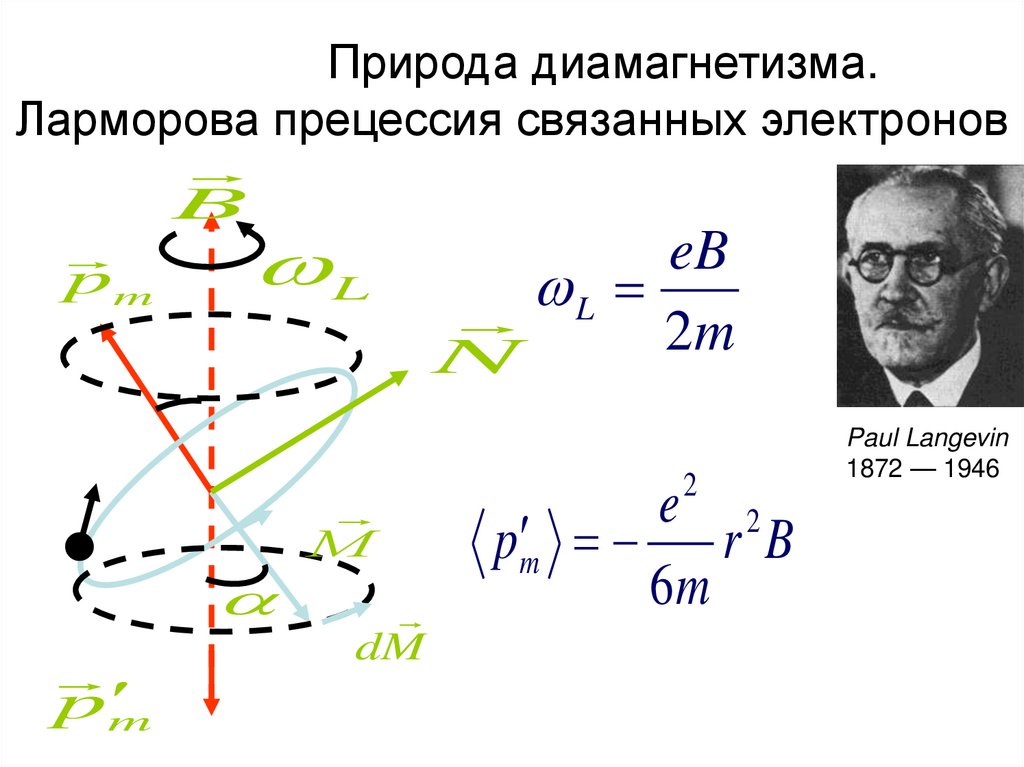
67. Природа диамагнетизма. Ларморова прецессия связанных электронов

B
eB
pm
L
N
pm
М
dM
L
2m
2
e 2
pm r B
6m
Paul Langevin
1872 — 1946

68.

Природа диамагнетизма.
Диамагнетизм свободных электронов
Ландау
v B
Скорость частицы
Лев Давидович
1908 - 1968
2
v
Сила Лоренца
F м q v; B m a n m ( e R )
R
2
mv
2
m
m 2 R
mv
R
R
T
q vB
qB T
qB
R
qB
2 2
e 2 e me v eB
pm IS R 2 2
B
Fм pм
T
e B 2 m
v
e
me v 2
pm
2B

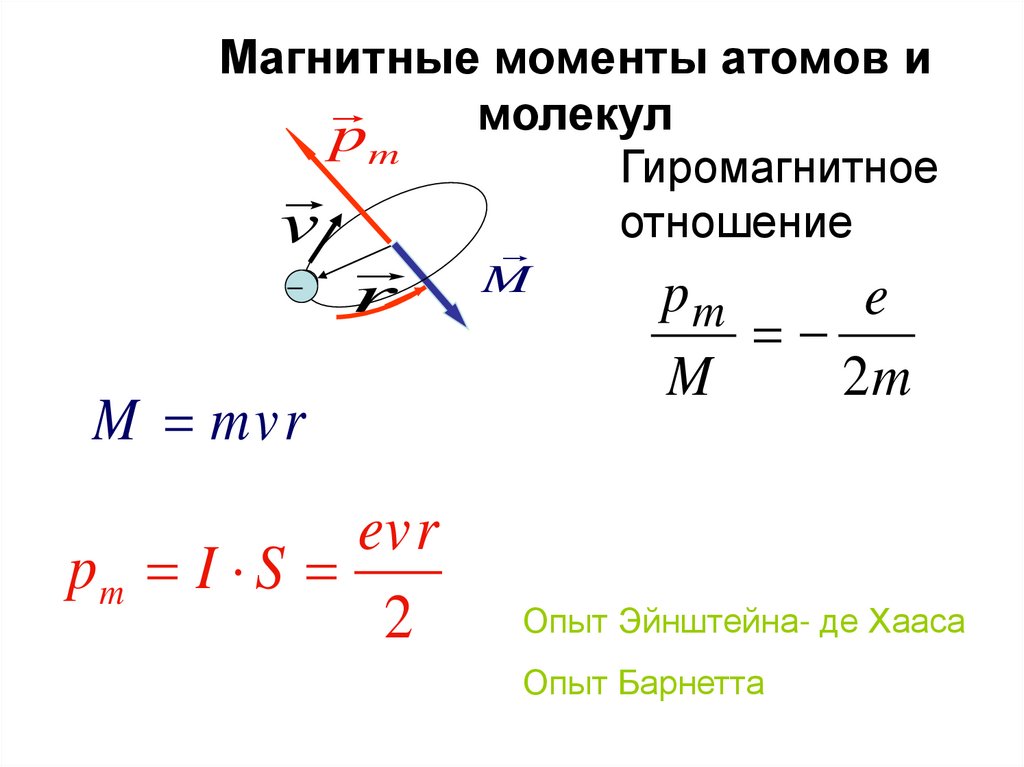
69. Магнитные моменты атомов и молекул

pm
Гиромагнитное
отношение
v
__
r
M mvr
evr
pm I S
2
M
pm
e
M
2m
Опыт Эйнштейна- де Хааса
Опыт Барнетта

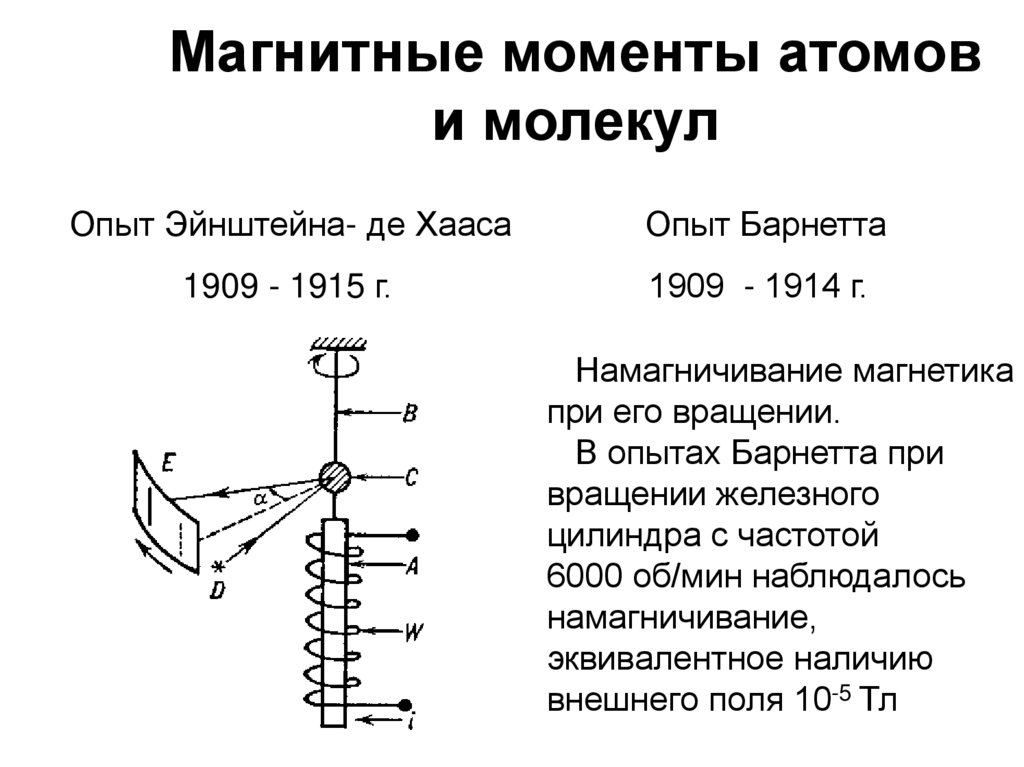
70. Магнитные моменты атомов и молекул

Опыт Эйнштейна- де Хааса
Опыт Барнетта
1909 - 1915 г.
1909 - 1914 г.
Намагничивание магнетика
при его вращении.
В опытах Барнетта при
вращении железного
цилиндра с частотой
6000 об/мин наблюдалось
намагничивание,
эквивалентное наличию
внешнего поля 10-5 Тл

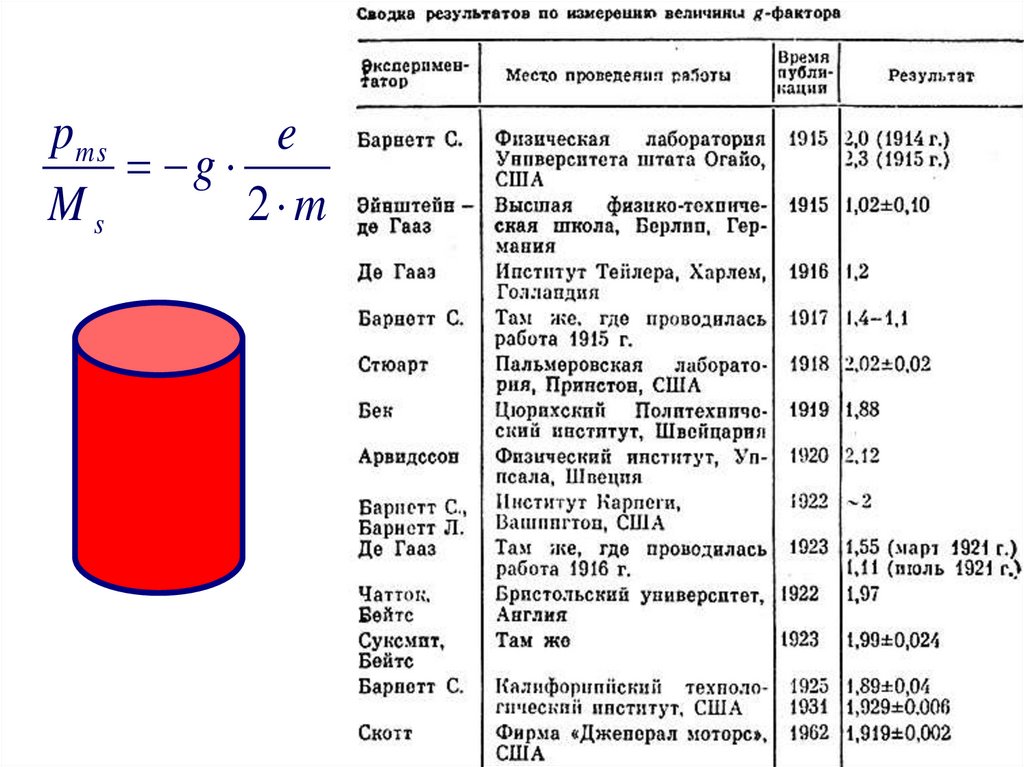
71.

p ms
e
g
Ms
2 m

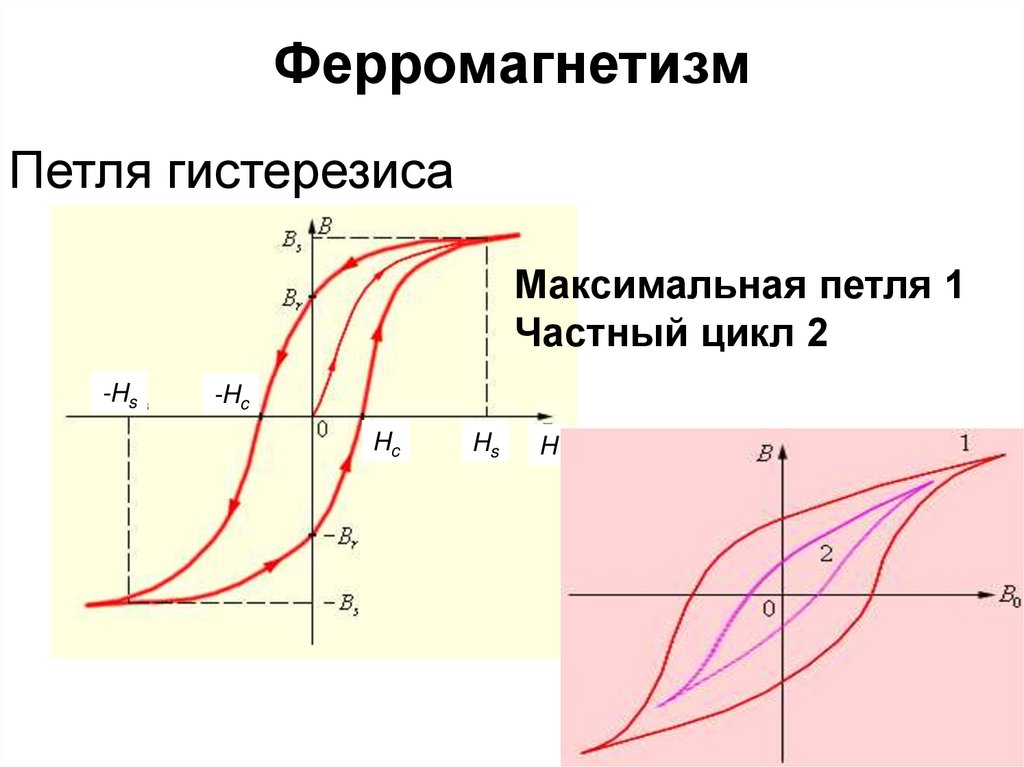
72. Ферромагнетизм

Петля гистерезиса
Максимальная петля 1
Частный цикл 2
-Hs
-Hc
H
Hc
Hs
H
H

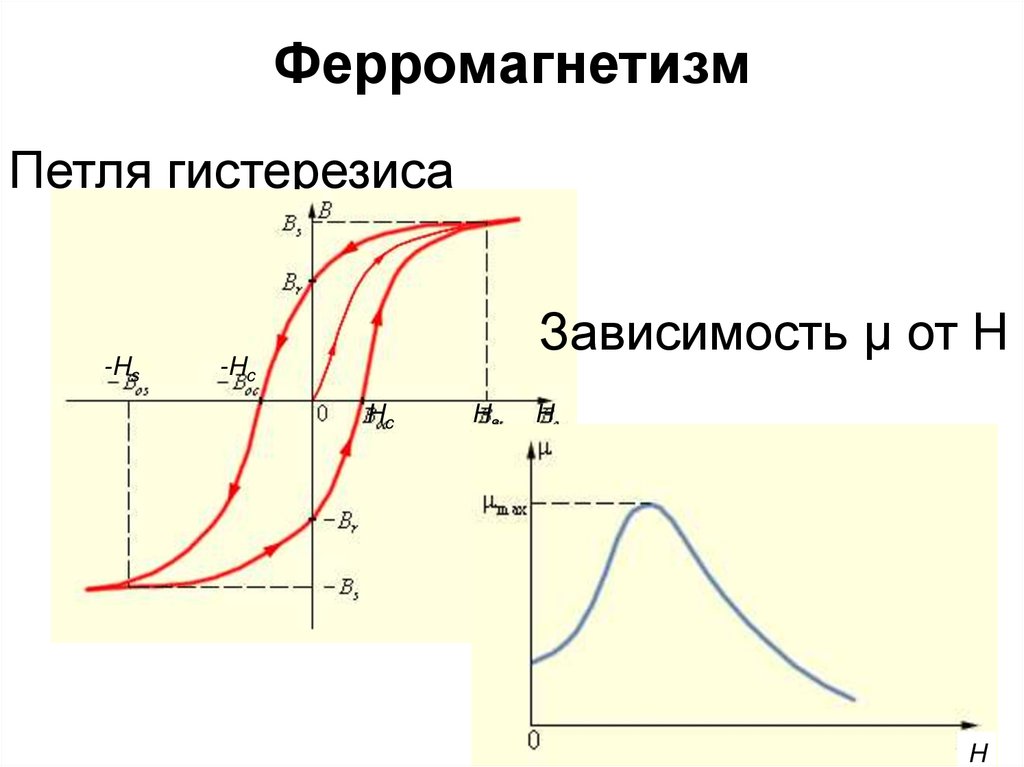
73. Ферромагнетизм

Петля гистерезиса
-Hs
Зависимость μ от Н
-Hc
Hc
Hs
H
H

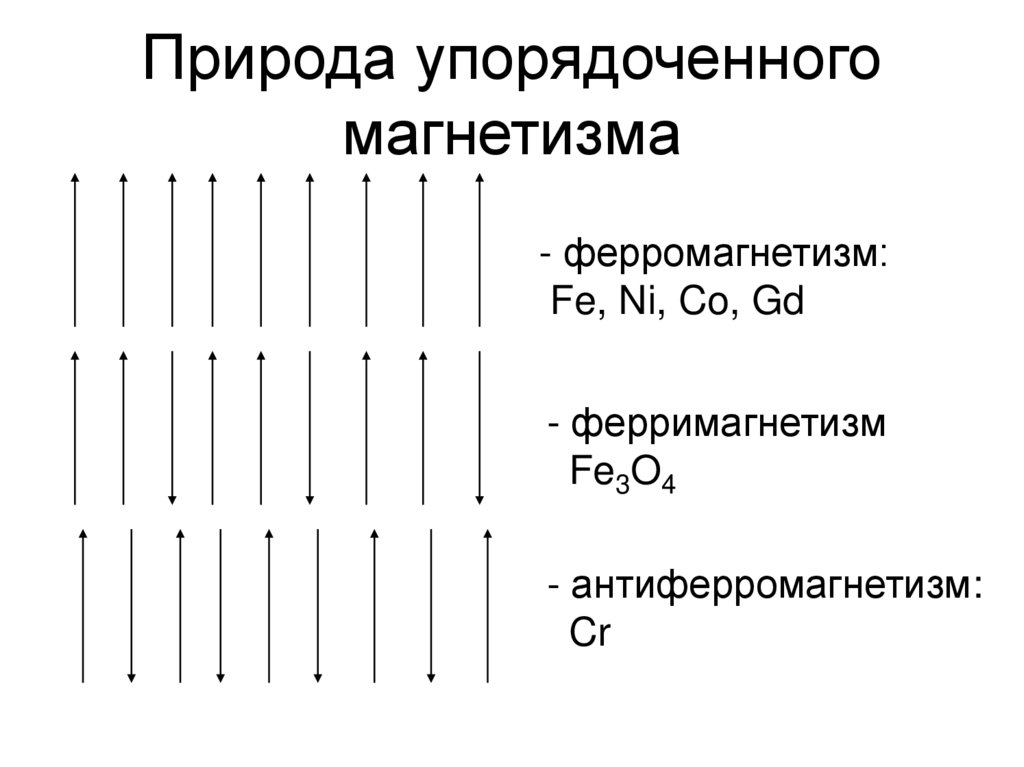
74. Природа упорядоченного магнетизма

- ферромагнетизм:
Fe, Ni, Co, Gd
- ферримагнетизм
Fe3O4
- антиферромагнетизм:
Cr

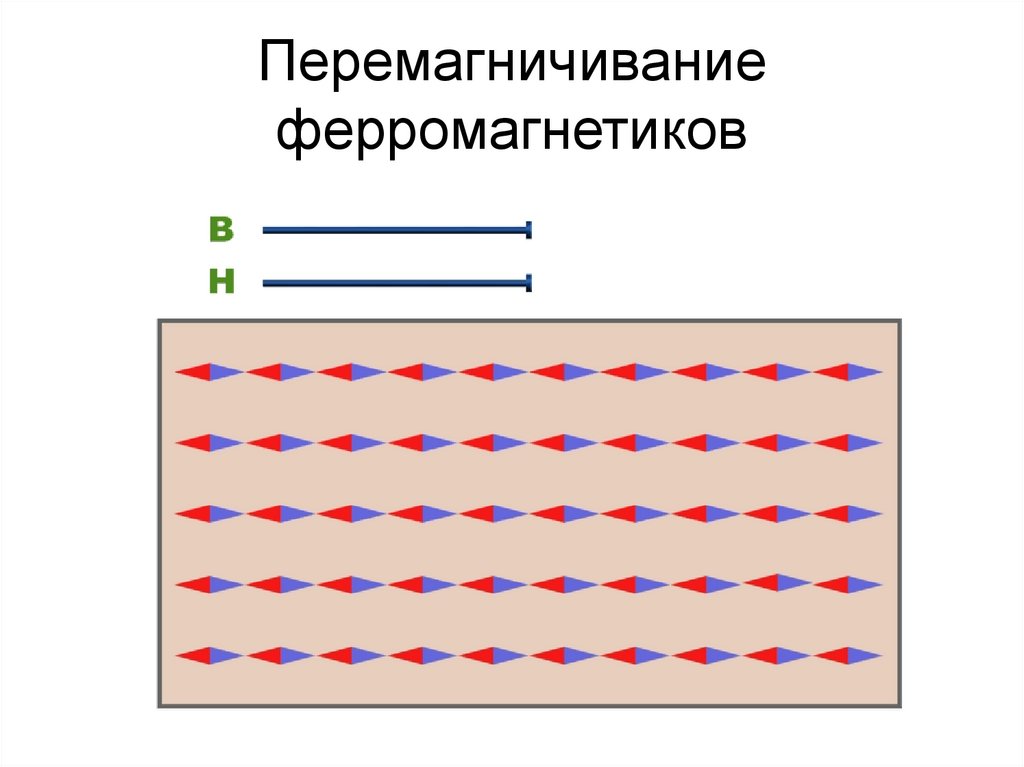
75. Перемагничивание ферромагнетиков

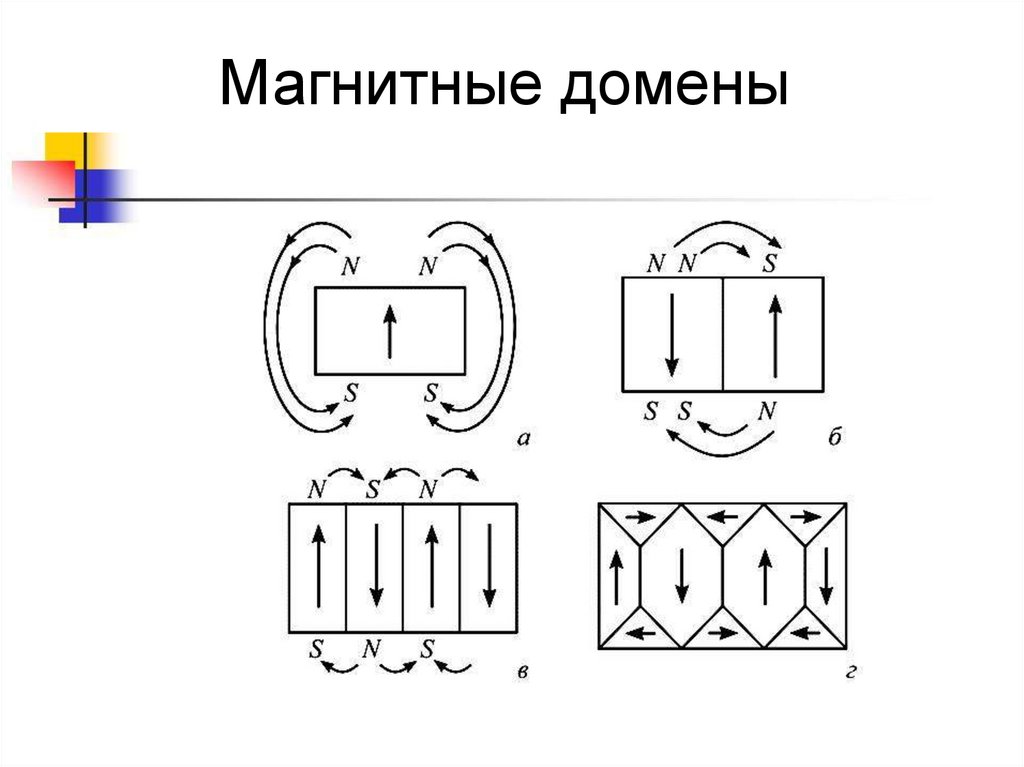
76. Магнитные домены

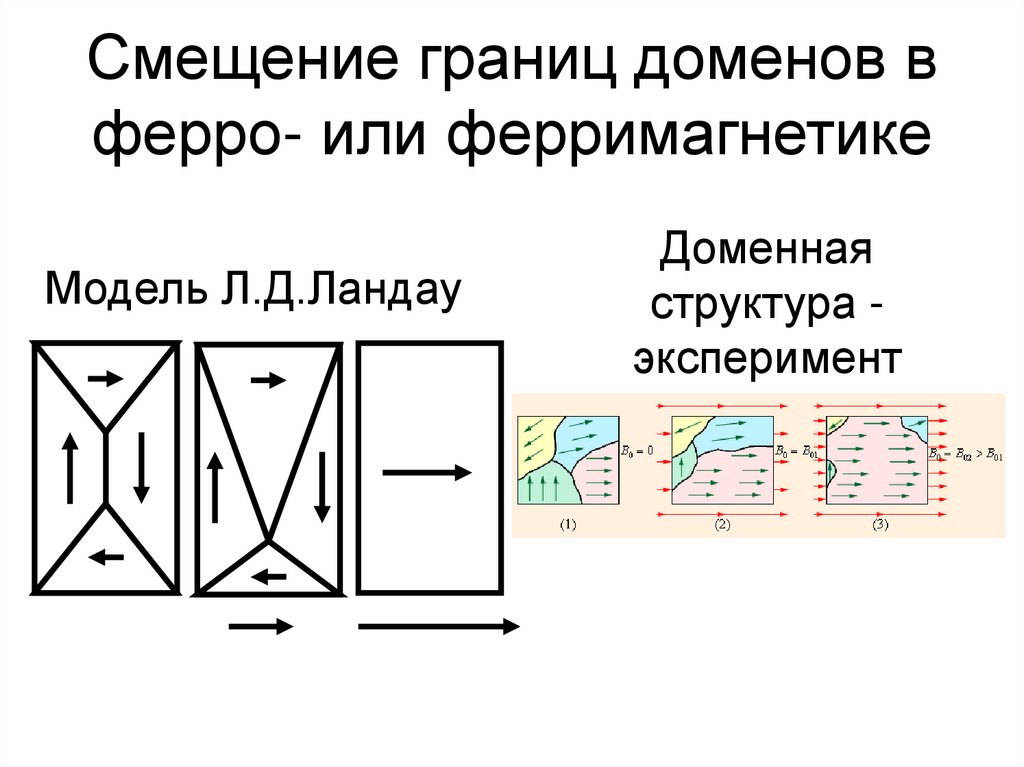
77. Смещение границ доменов в ферро- или ферримагнетике

Модель Л.Д.Ландау
Доменная
структура эксперимент

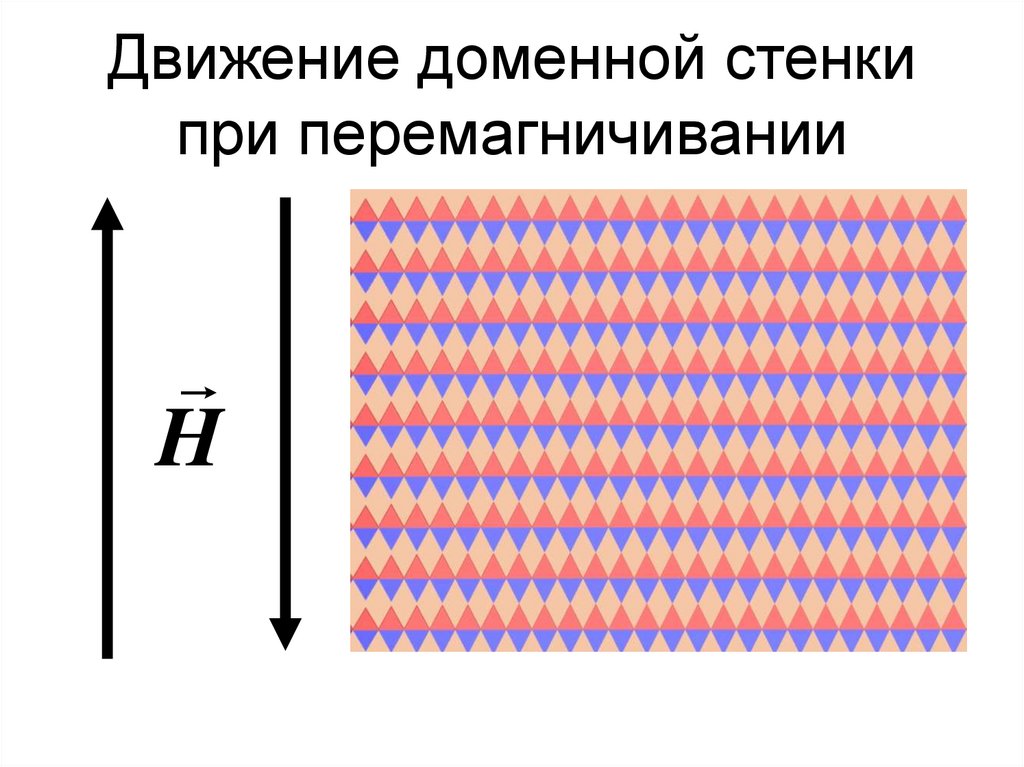
78. Движение доменной стенки при перемагничивании

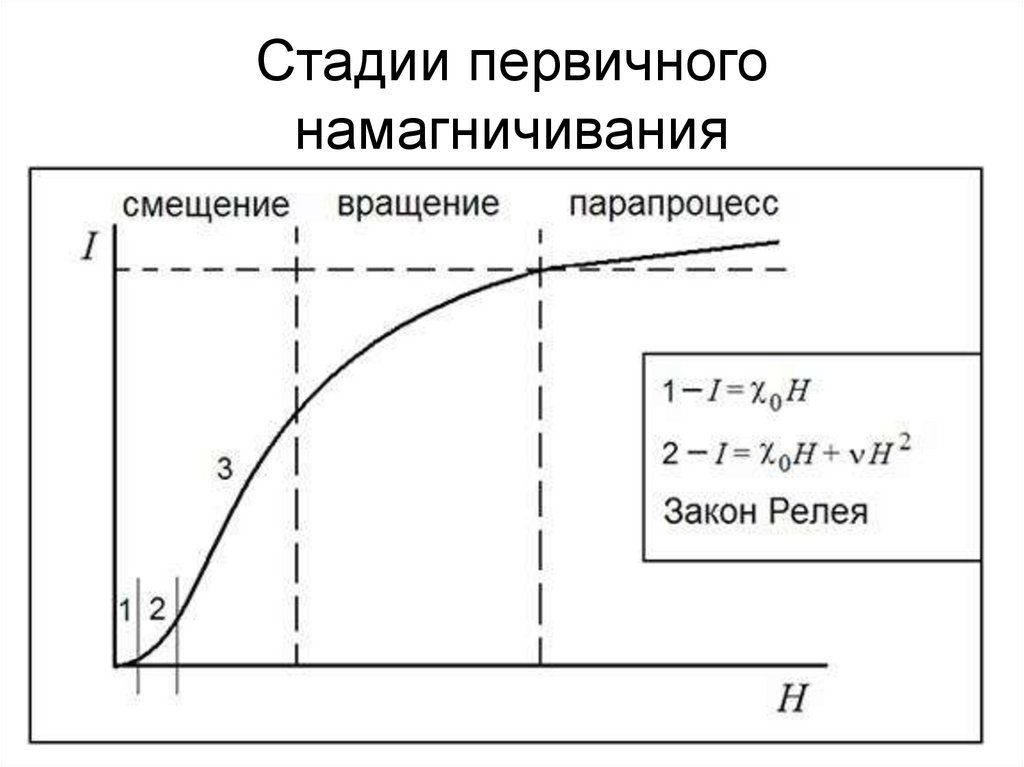
H

79. Стадии первичного намагничивания

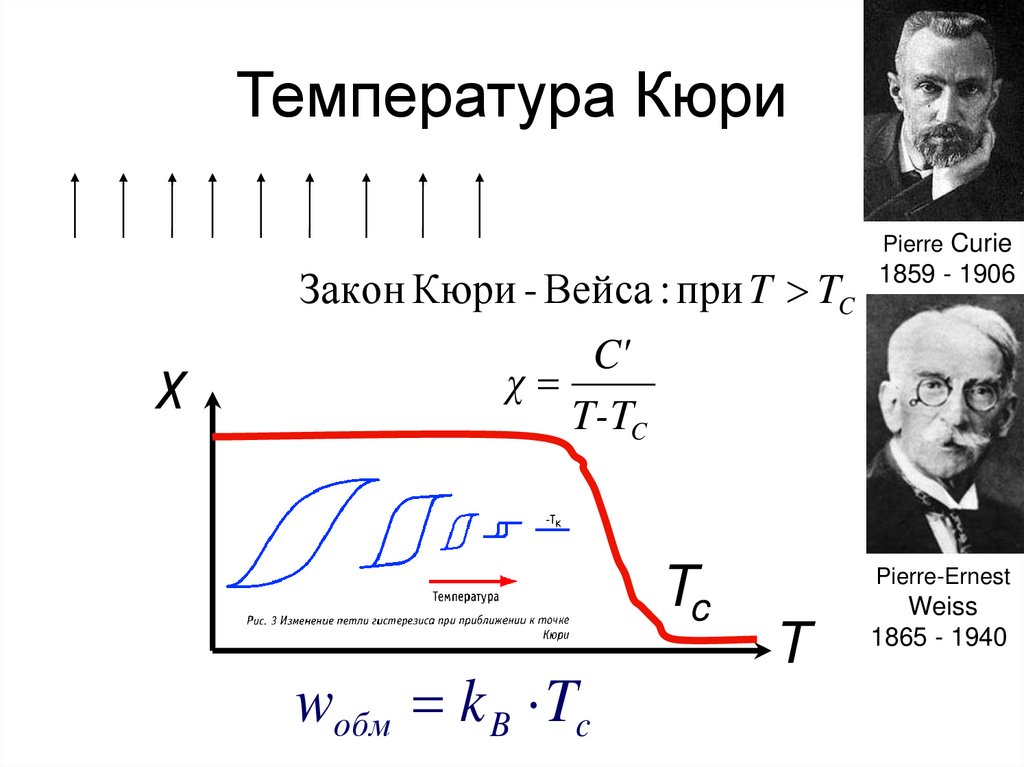
80. Температура Кюри

Pierre Curie
Закон Кюри - Вейса : при T TC
χ
1859 - 1906
C'
χ
T-TC
Tc
wобм k B Tc
Pierre-Ernest
T
Weiss
1865 - 1940

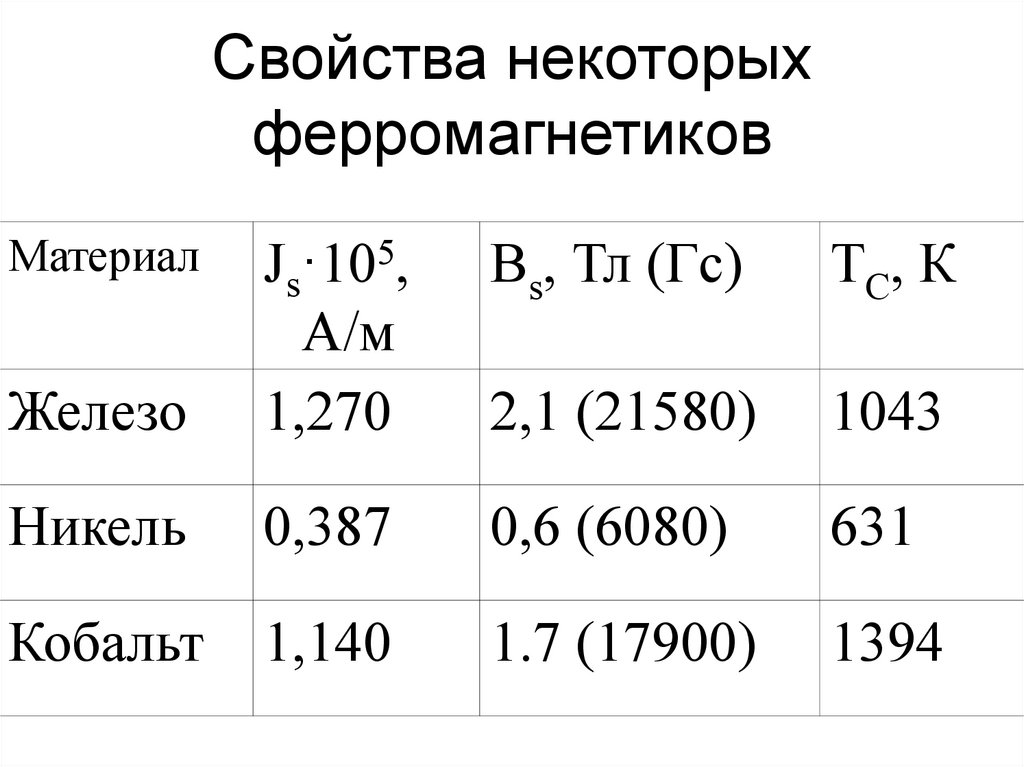
81. Свойства некоторых ферромагнетиков

Материал
Bs, Тл (Гс)
TC, К
Железо
Js·105,
А/м
1,270
2,1 (21580)
1043
Никель
0,387
0,6 (6080)
631
Кобальт
1,140
1.7 (17900)
1394

82. Визуализация магнитных силовых линий

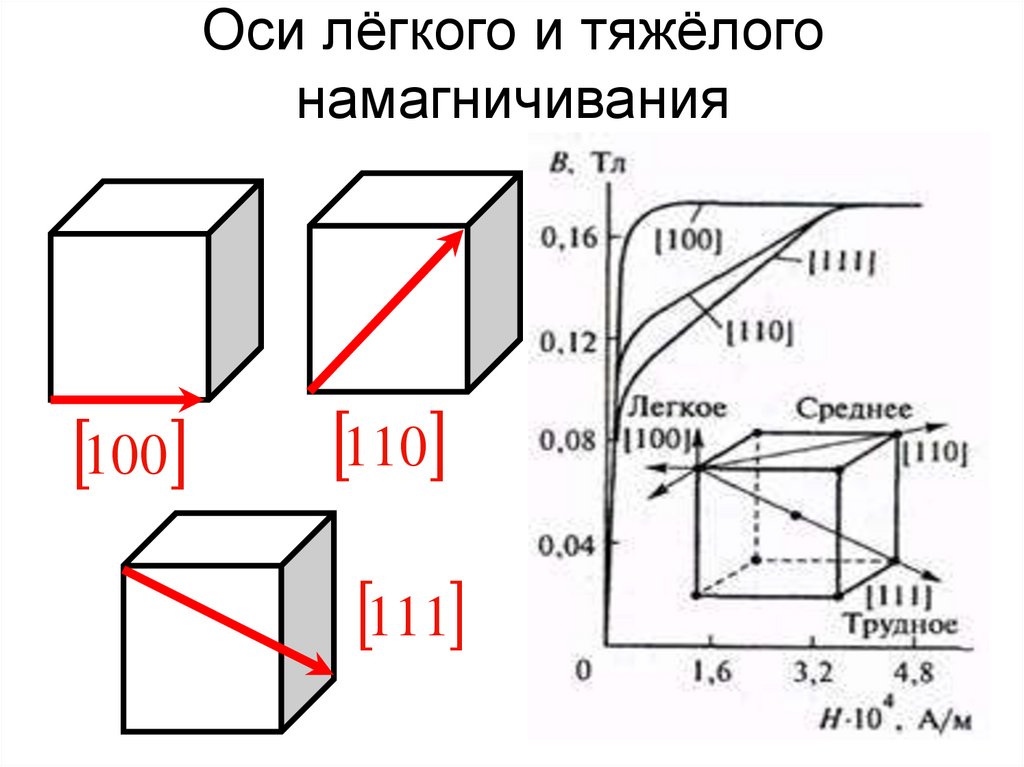
83. Оси лёгкого и тяжёлого намагничивания

100
110
111

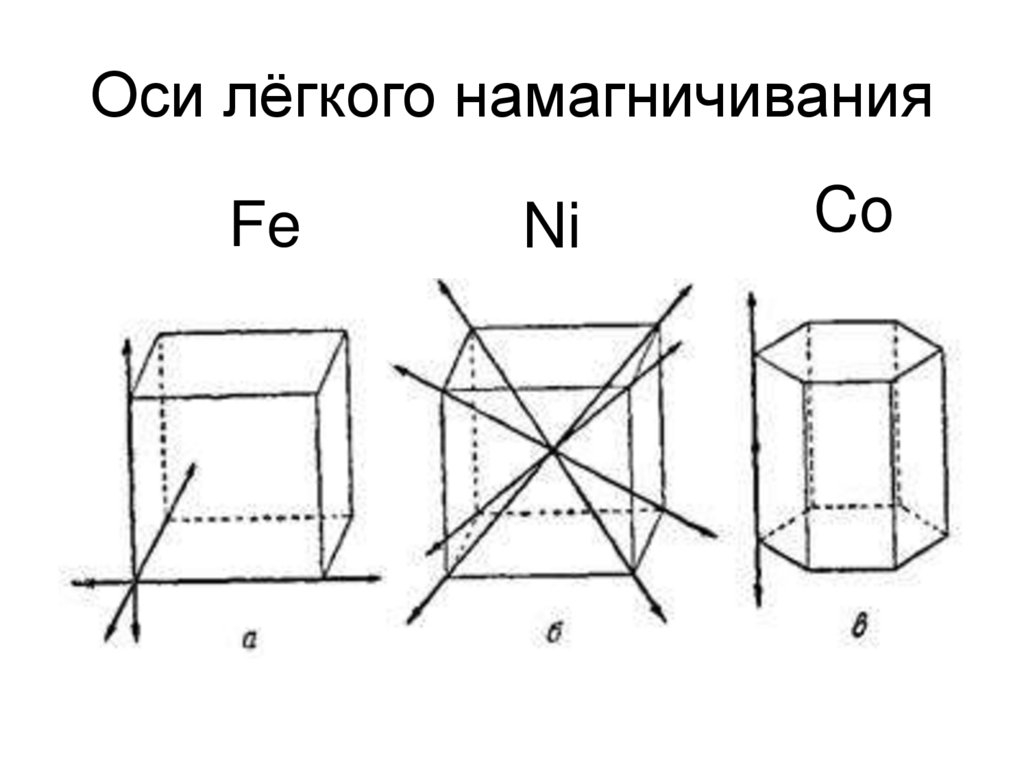
84. Оси лёгкого намагничивания

Fe
Ni
Co

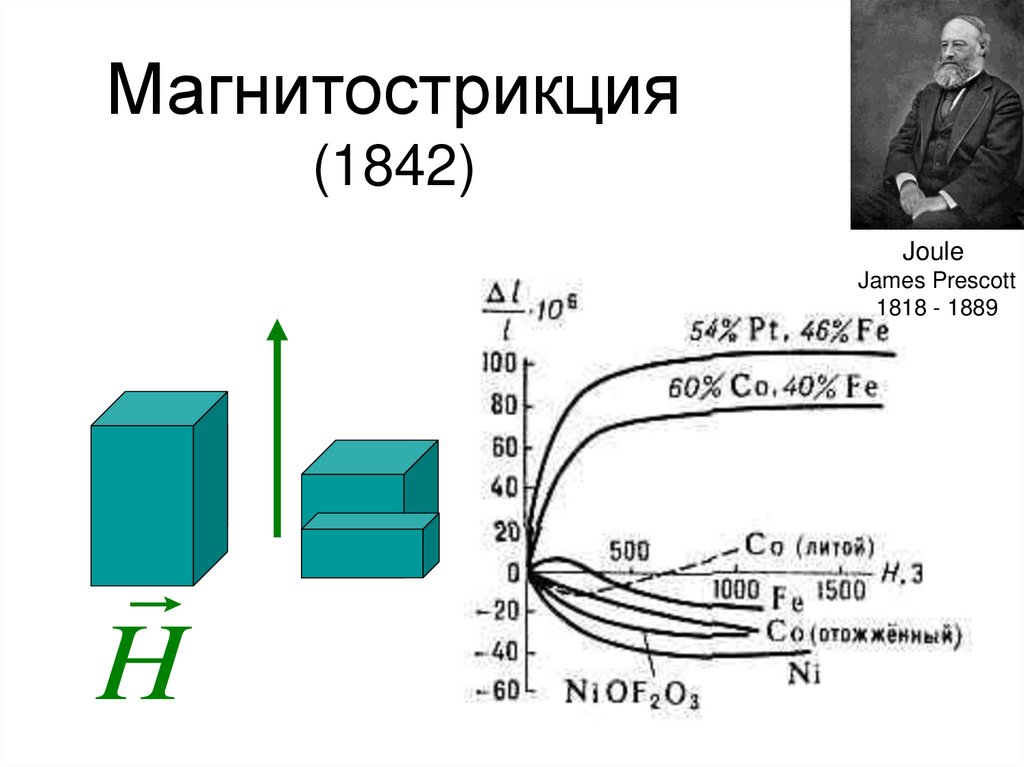
85. Магнитострикция (1842)

Joule
James Prescott
1818 - 1889
H

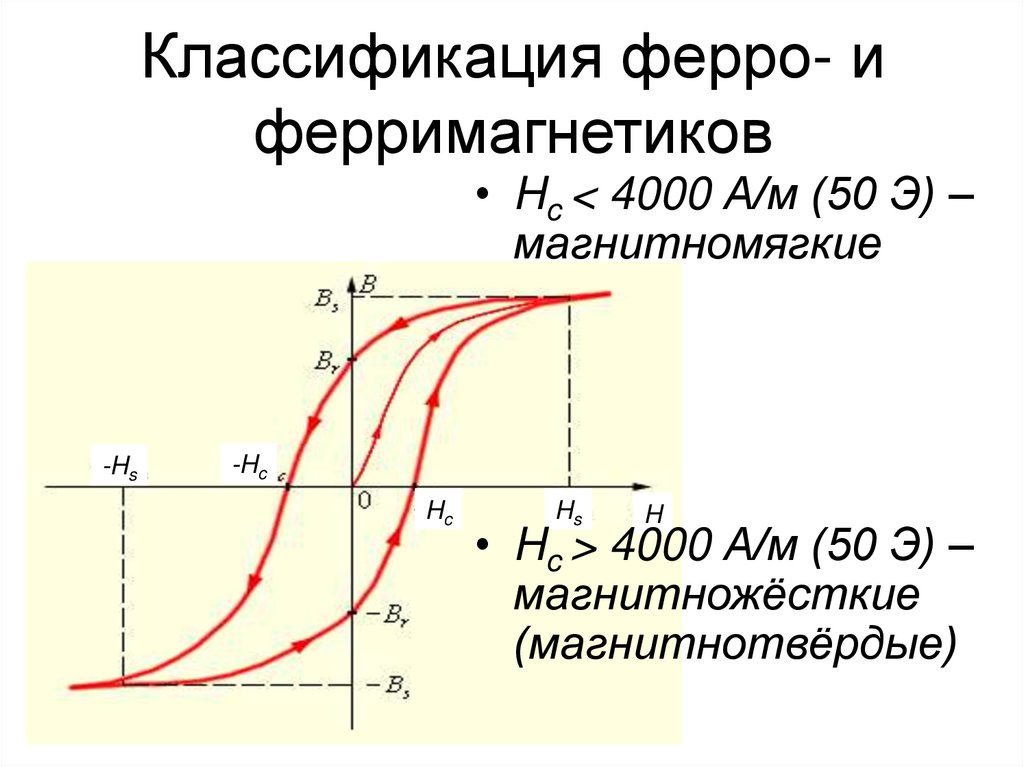
86. Классификация ферро- и ферримагнетиков

• Hc < 4000 А/м (50 Э) –
магнитномягкие
-Hs
-Hc
Hc
Hs
H
• Hc > 4000 А/м (50 Э) –
магнитножёсткие
(магнитнотвёрдые)

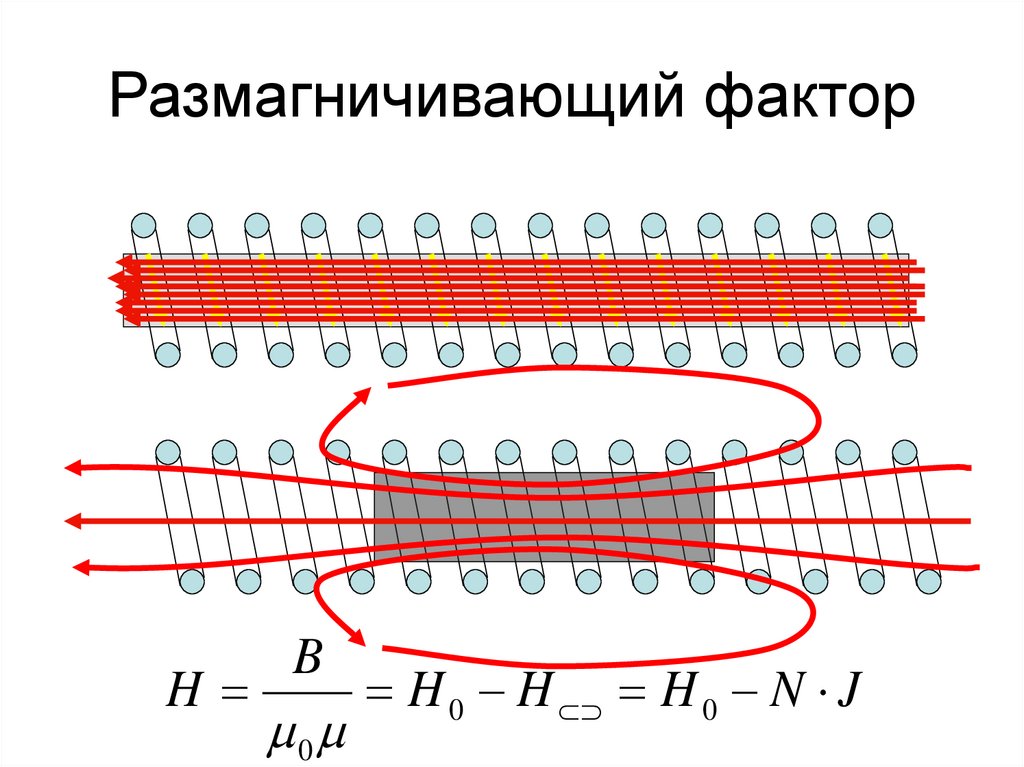
87. Размагничивающий фактор

H
B
0
H 0 H H 0 N J

88. Размагничивающий фактор

H
B
H 0 H H 0 N J
0
J ( 1) H
B
0
H 0 N ( 1)
0 H 0
B
1 N ( 1)
B
0

89. Значения размагничивающего фактора

Для эллипсоидов вращения (b = с) значение Na
может быть вычислено по формулам
где γ=a/b.
В единицах СИ Na + Nb + Nc = 1, поэтому для
однородного шара Na = Nb = Nc = 1/3.

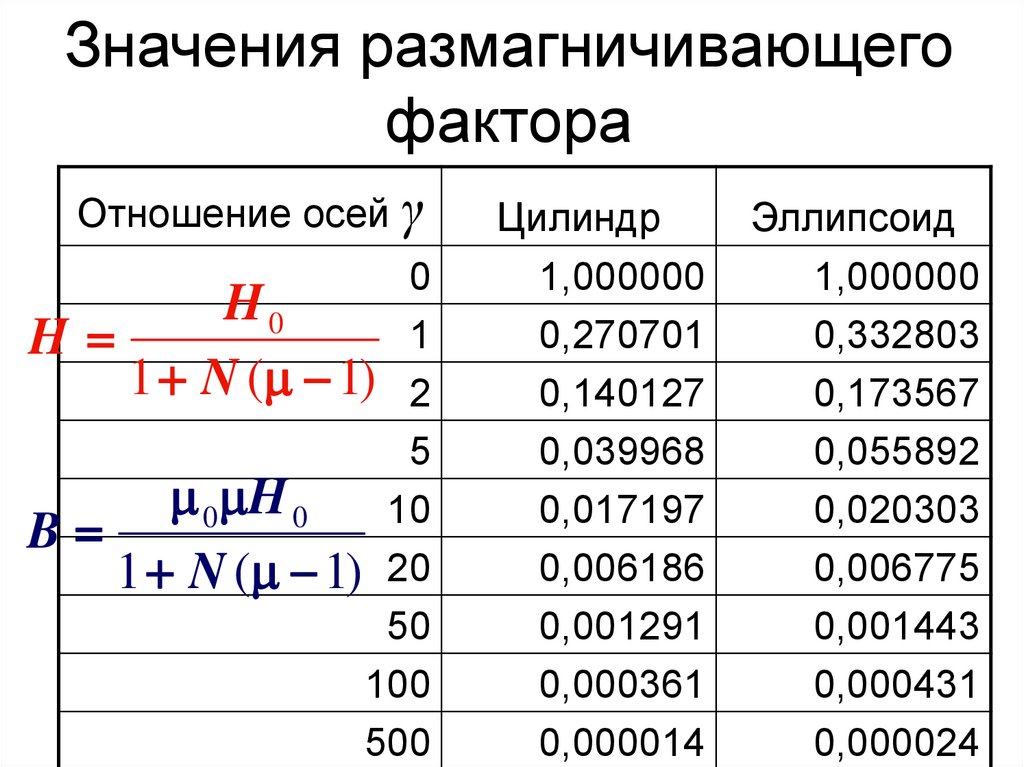
90. Значения размагничивающего фактора

Отношение осей γ
0
H0
1
H
1 N ( 1) 2
5
0 H 0
10
B
1 N ( 1) 20
50
100
500
Цилиндр
1,000000
0,270701
0,140127
0,039968
0,017197
0,006186
0,001291
0,000361
0,000014
Эллипсоид
1,000000
0,332803
0,173567
0,055892
0,020303
0,006775
0,001443
0,000431
0,000024

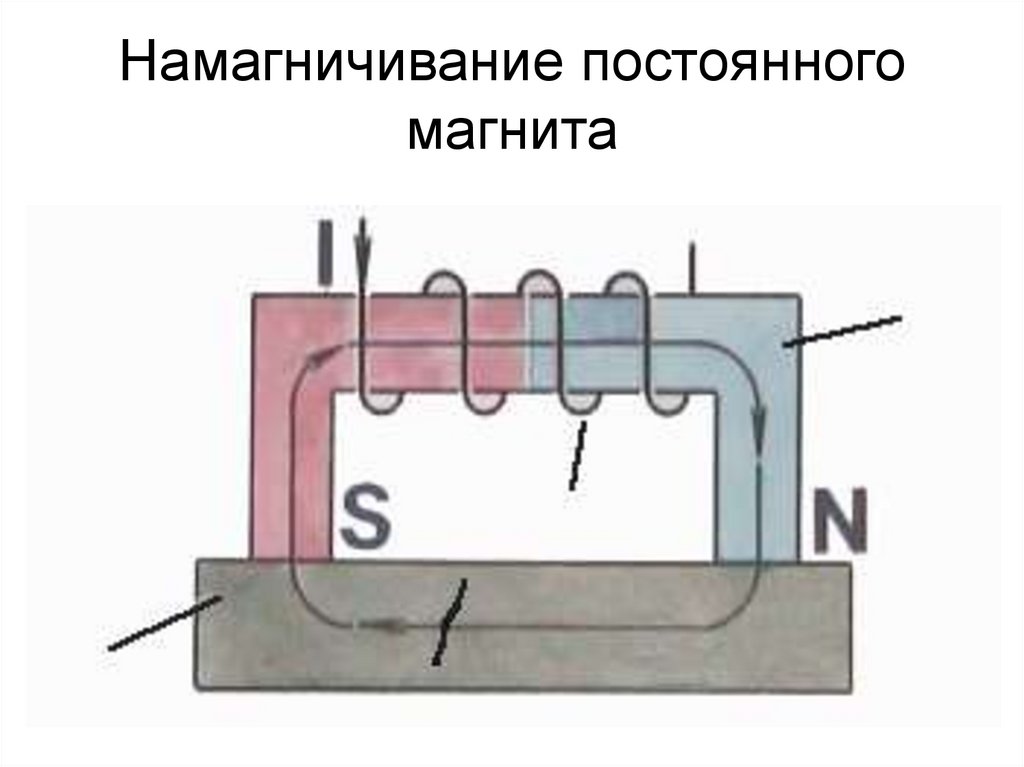
91. Намагничивание постоянного магнита

92. ЭЛЕМЕНТЫ ЗОННОЙ ТЕОРИИ ТВЕРДЫХ ТЕЛ

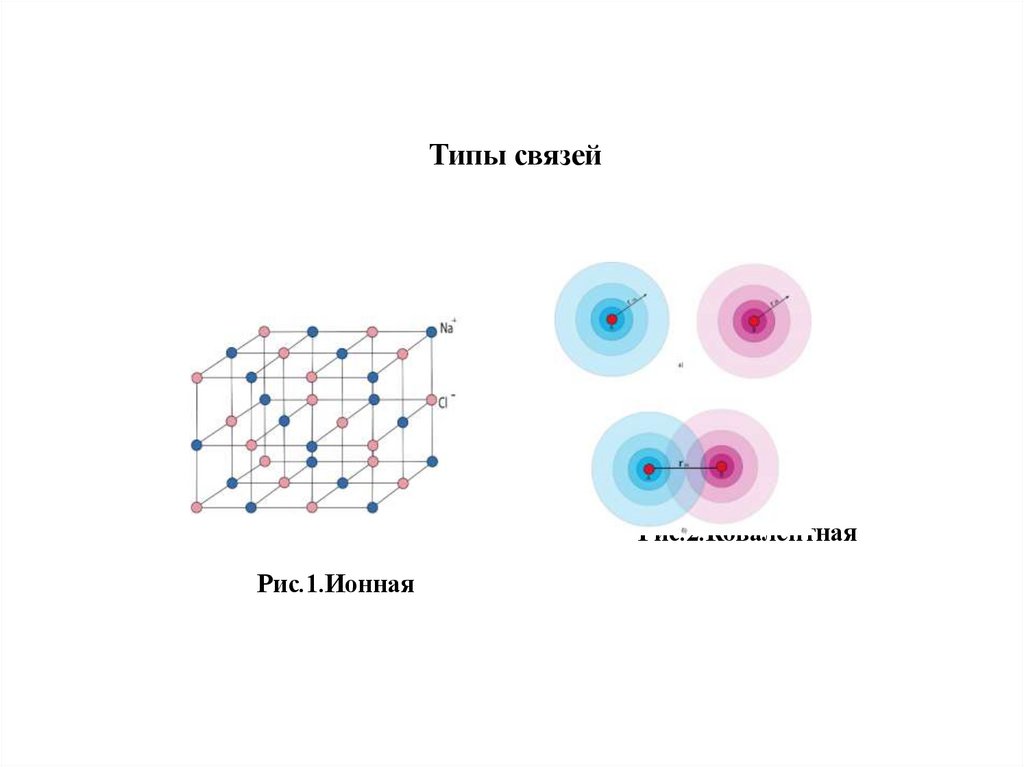
93. Типы связей

Рис.2.Ковалентная
Рис.1.Ионная

94.

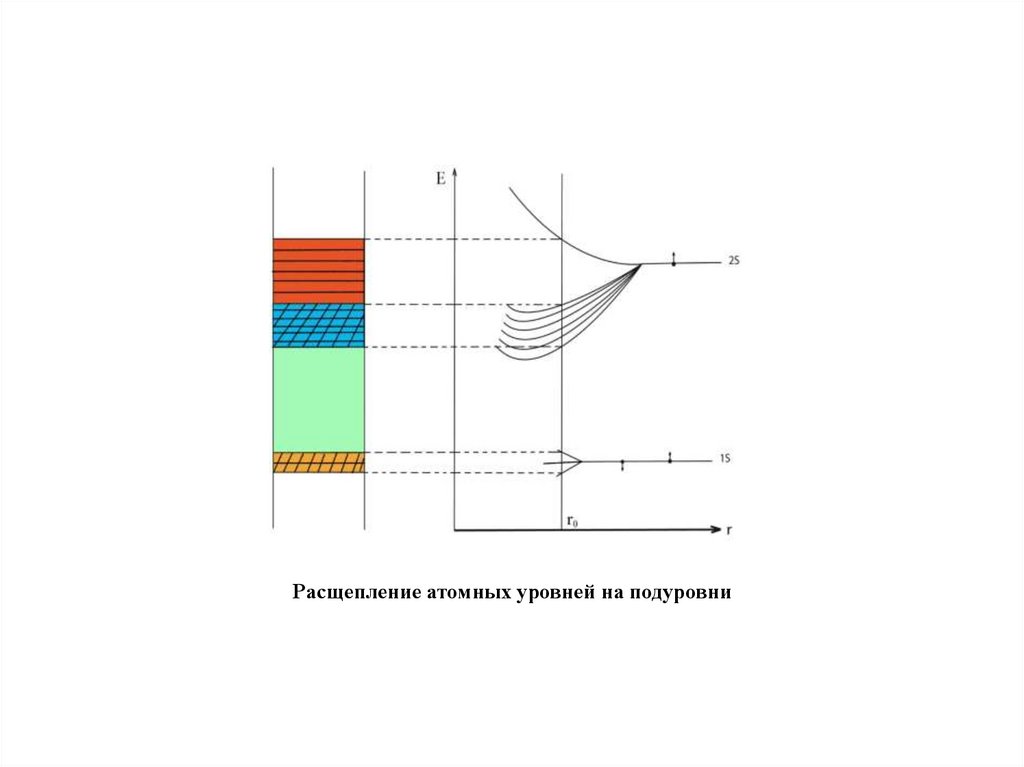
Расщепление атомных уровней на подуровни

95.

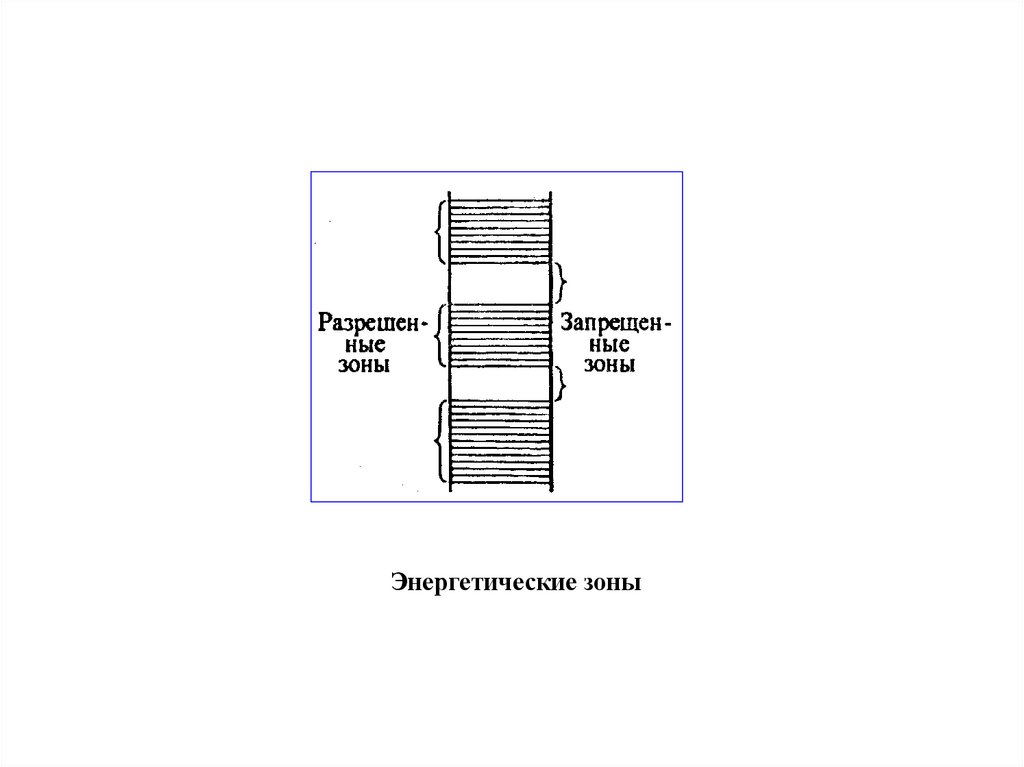
Энергетические зоны

96.

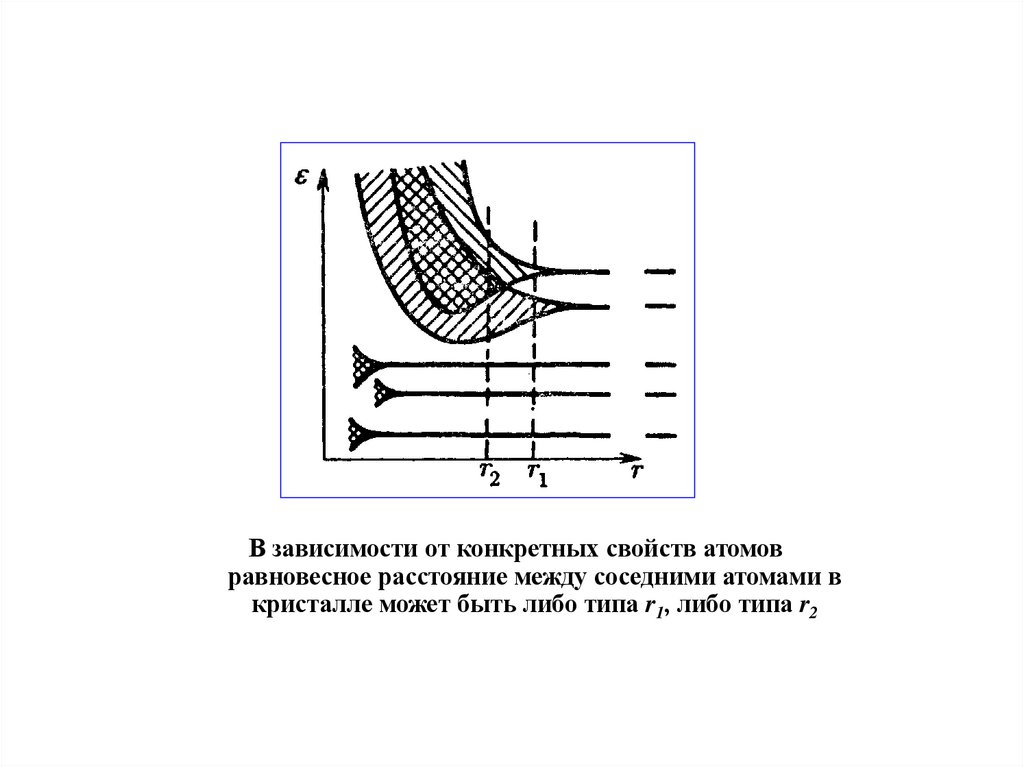
В зависимости от конкретных свойств атомов
равновесное расстояние между соседними атомами в
кристалле может быть либо типа r1, либо типа r2

97.

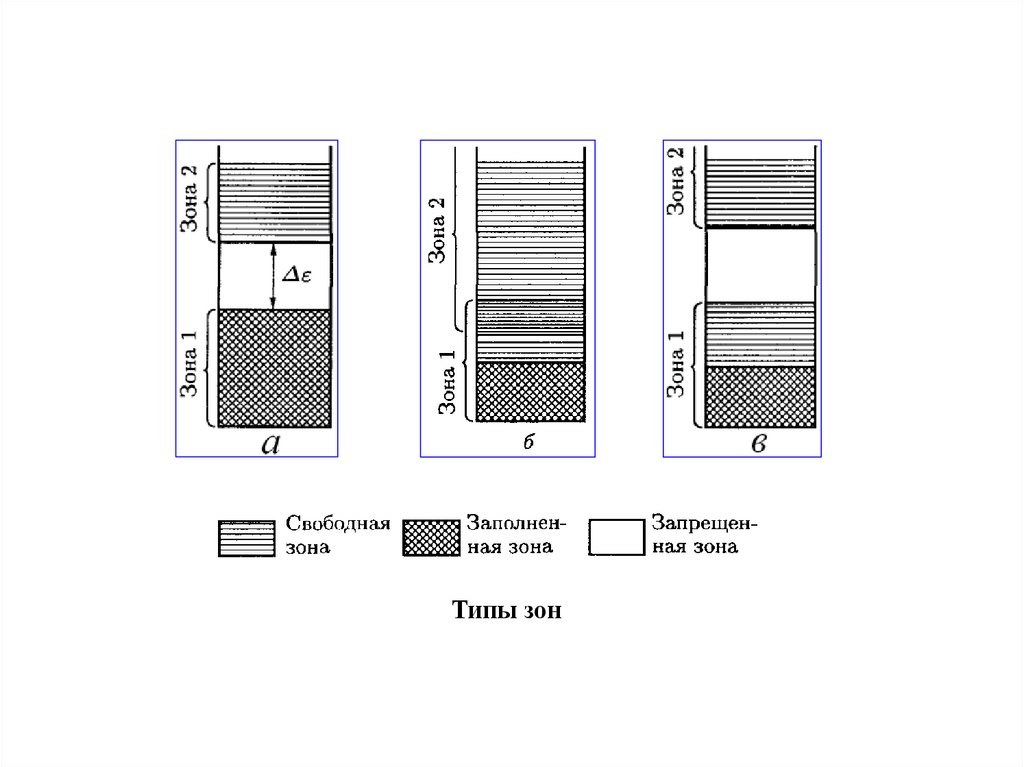
Типы зон

98.

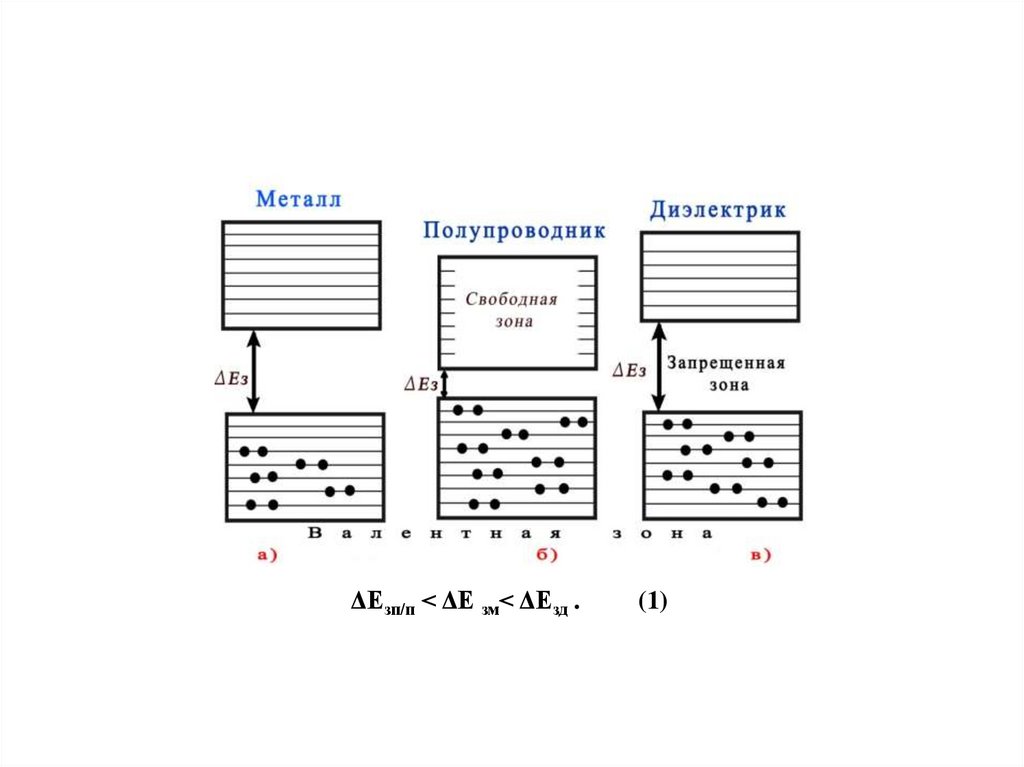
ΔЕзп/п < ΔΕ зм< ΔΕзд .
(1)

99.

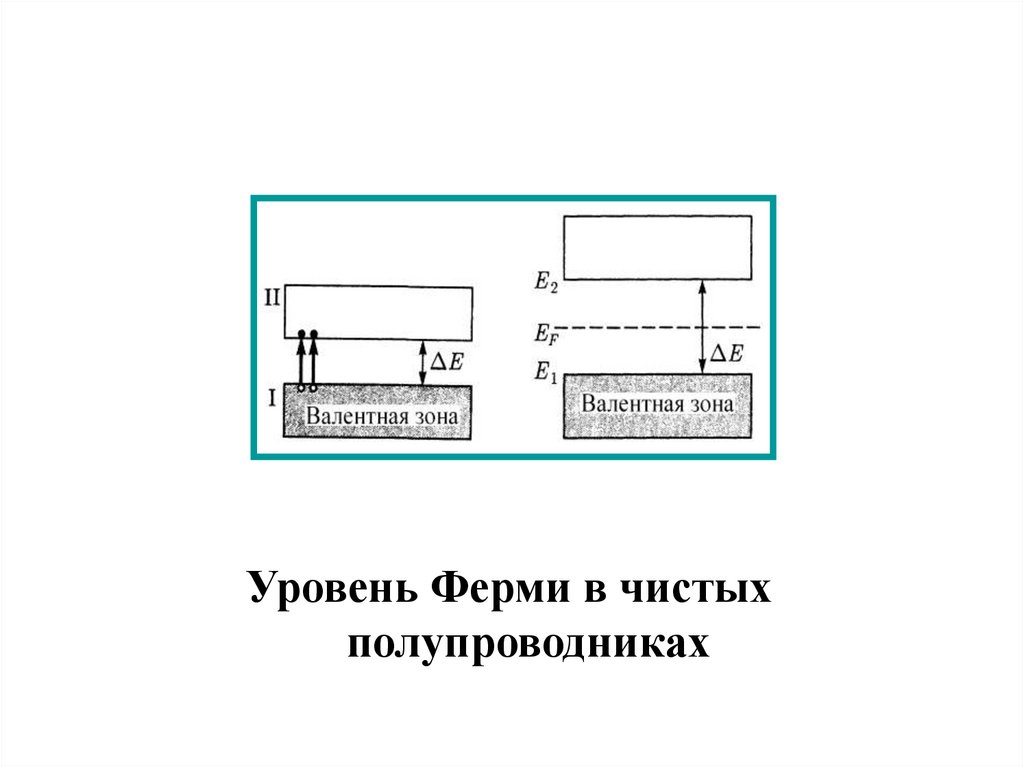
Уровень Ферми в чистых
полупроводниках

100. Уровень Ферми

(2)
1
Е фп / п E1 Е зп / п
2
h 3n
Еф Eф E1
2m 8
2
2
3
(3)
n –концентрация свободных носителей заряда
N
n
V

101.

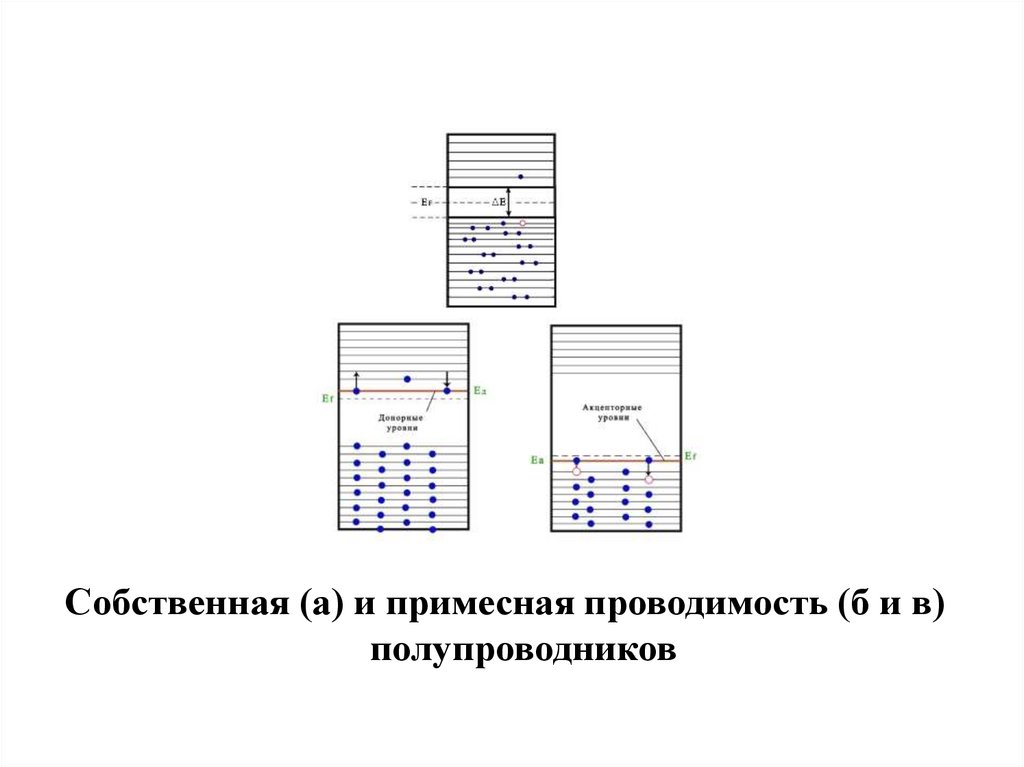
Собственная (а) и примесная проводимость (б и в)
полупроводников

102.

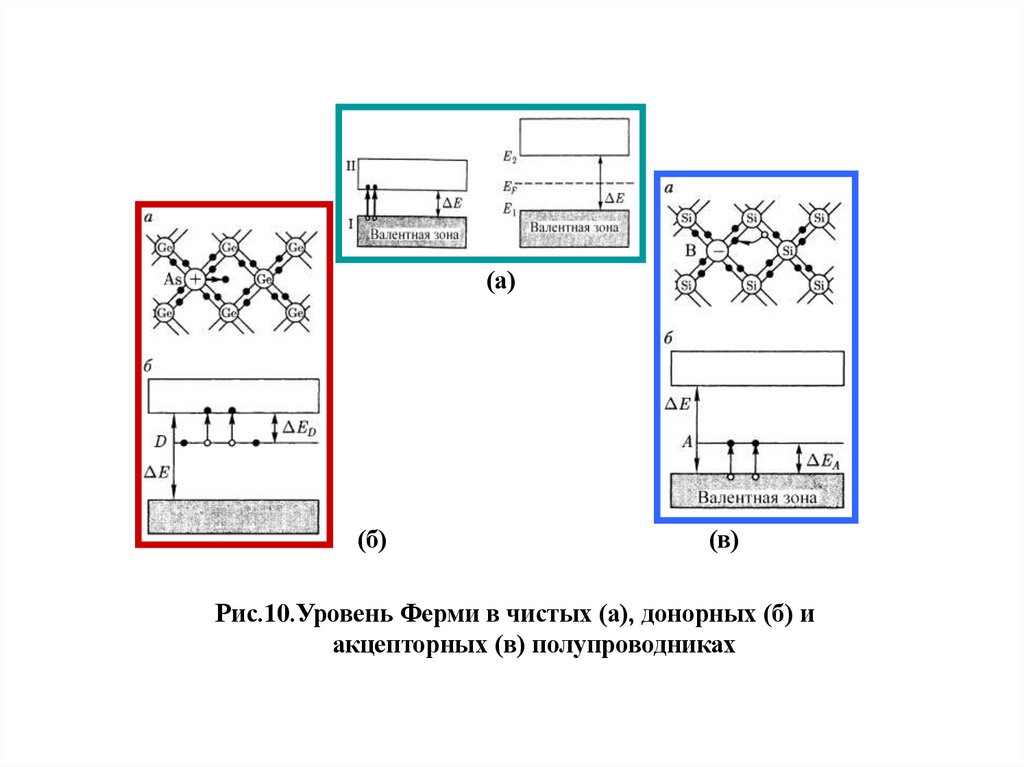
(а)
(б)
(в)
Рис.10.Уровень Ферми в чистых (а), донорных (б) и
акцепторных (в) полупроводниках

103.

Примеси в полупроводниках изменяют уровень Ферми :
для полупроводников с собственной проводимостью
1
Е ф Е зп / п
2
Еф
для донорных полупроводников Δ
1
Е зп / п
>2
1
Е зп / п
2
для акцепторных полупроводников
ΔЕ ф<

104.

Закон Ома в дифференциальной
форме
J E
(4)
E enu
J enu
u
E
en
(5)
(7)
(6)
(8)

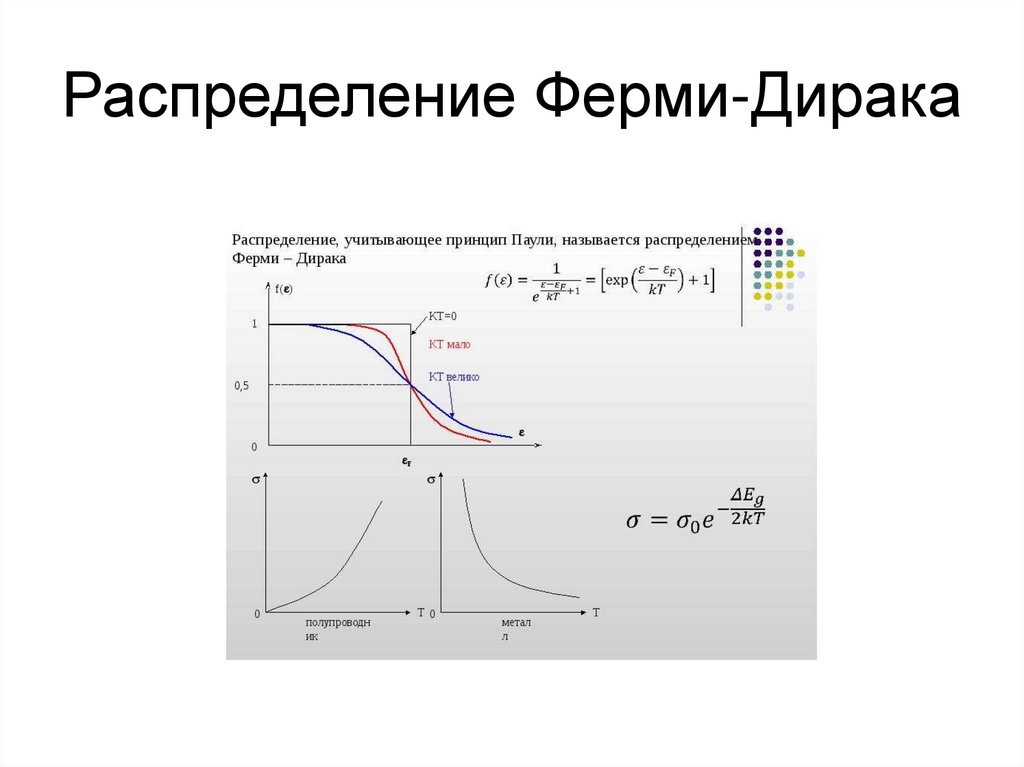
105. Распределение Ферми-Дирака

106.

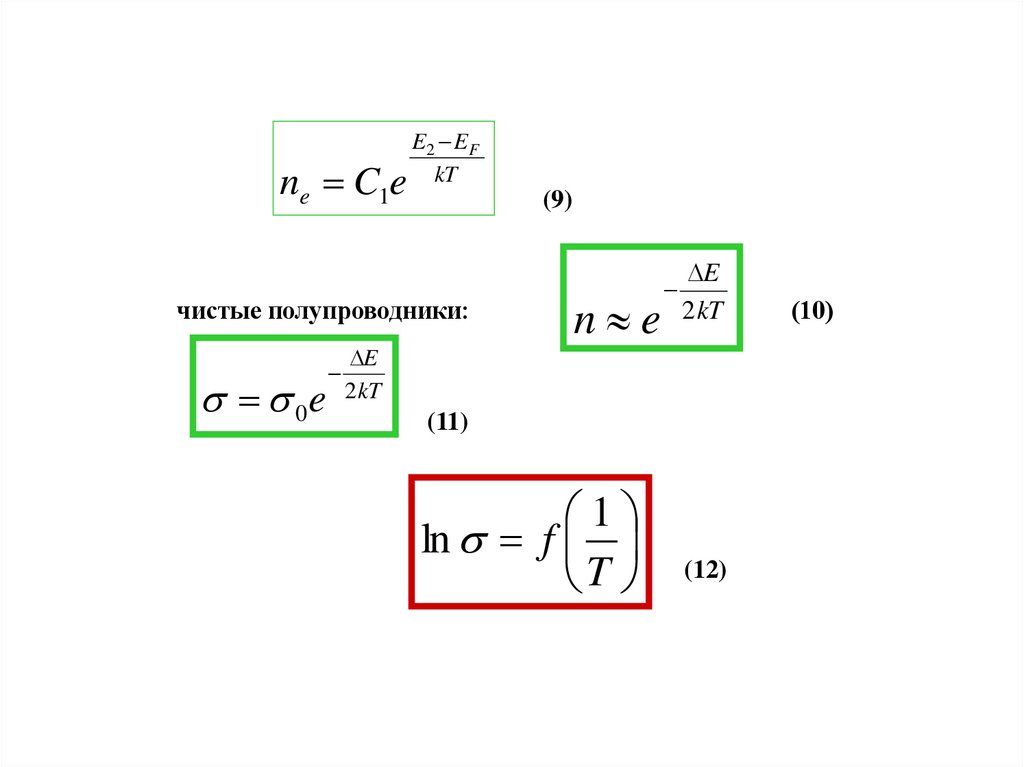
ne C1e
E2 E F
kT
(9)
чистые полупроводники:
0e
E
2 kT
n e
E
2 kT
(11)
1
ln f
T
(12)
(10)

107.

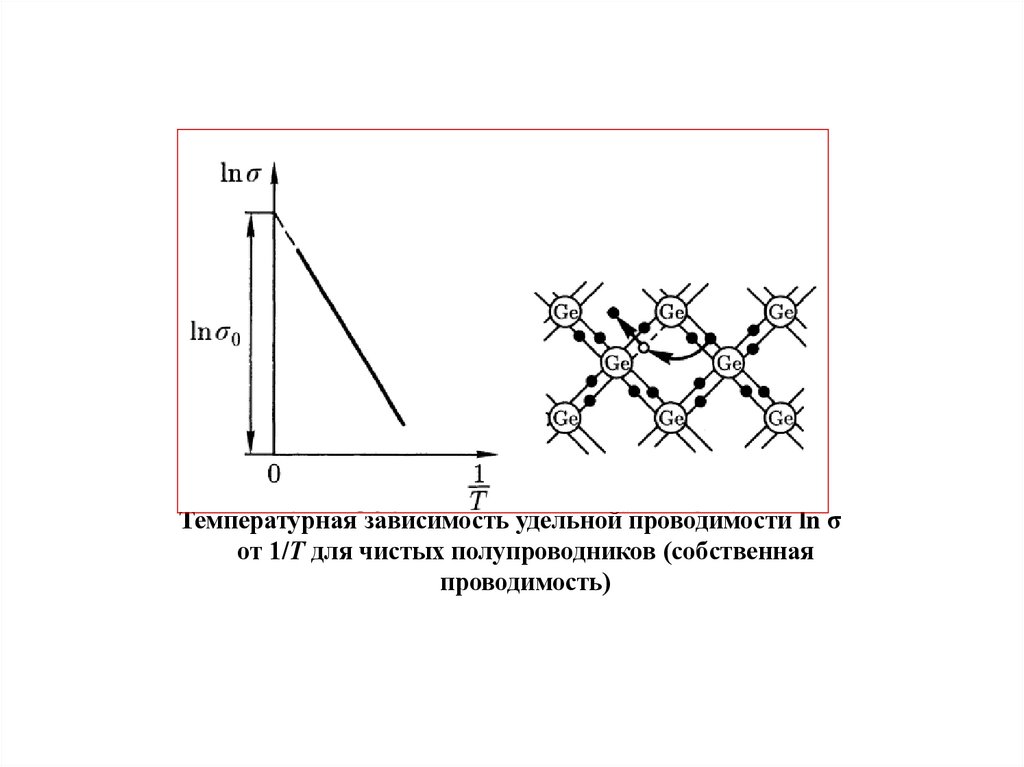
Температурная зависимость удельной проводимости ln σ
от 1/Т для чистых полупроводников (собственная
проводимость)

108.

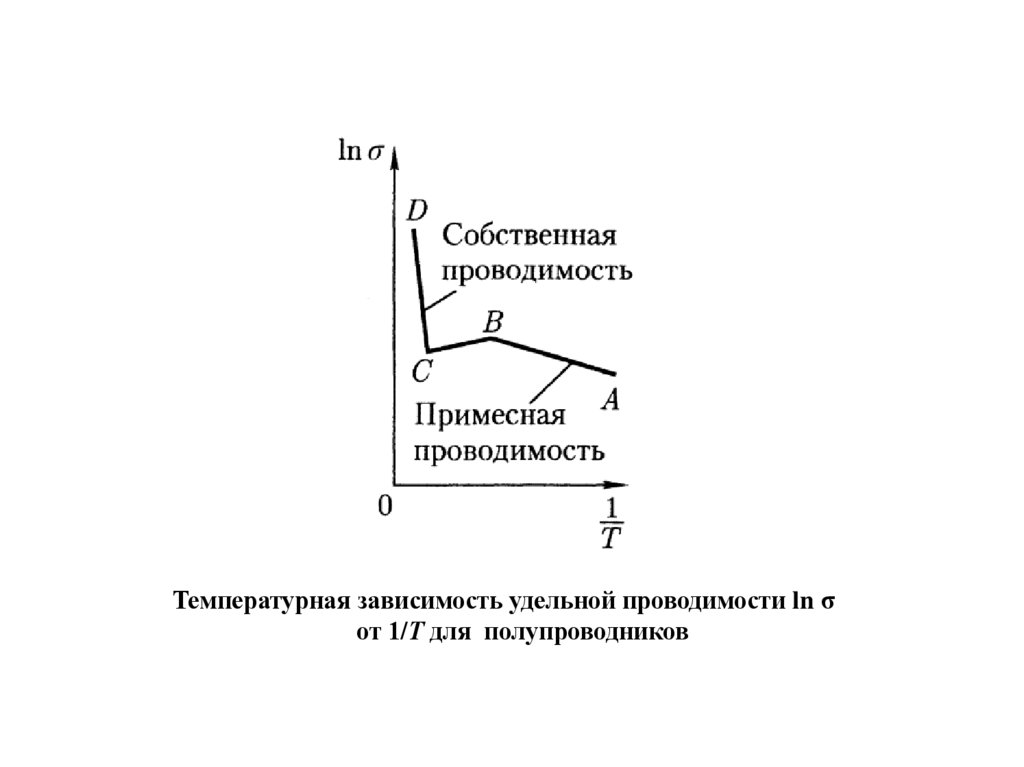
Температурная зависимость удельной проводимости ln σ
от 1/Т для полупроводников

109.

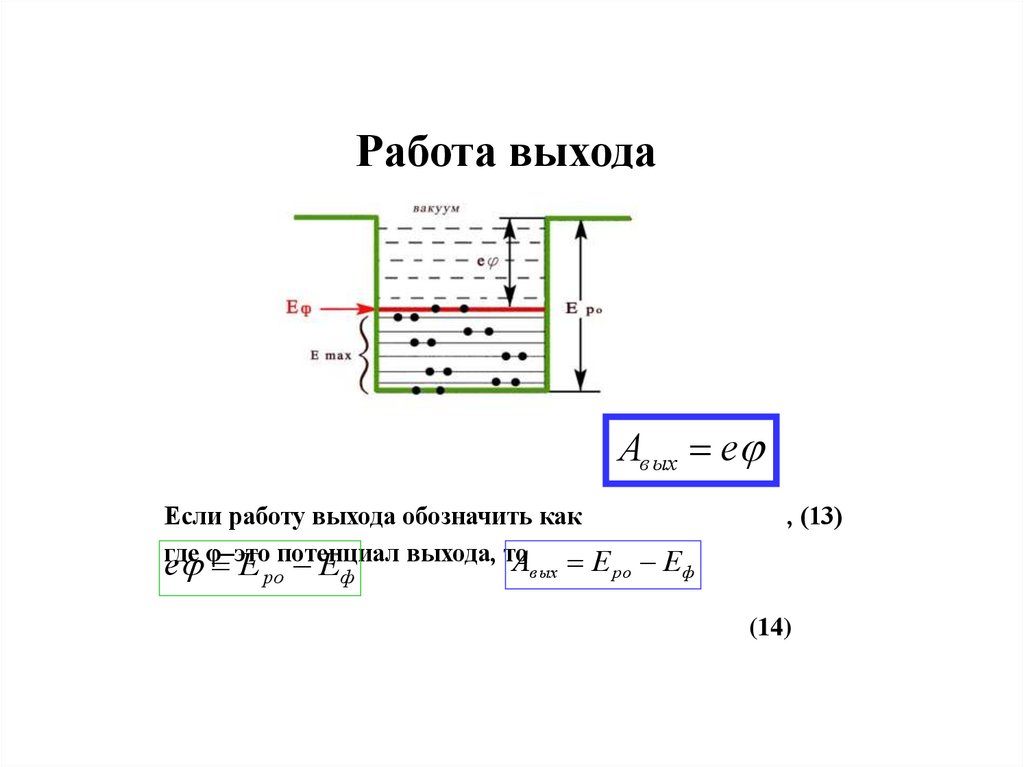
Работа выхода
Авых е
Если работу выхода обозначить как
где φ–это потенциал выхода, то
А Е
е Е ро Еф
в ых
, (13)
ро
Еф
(14)

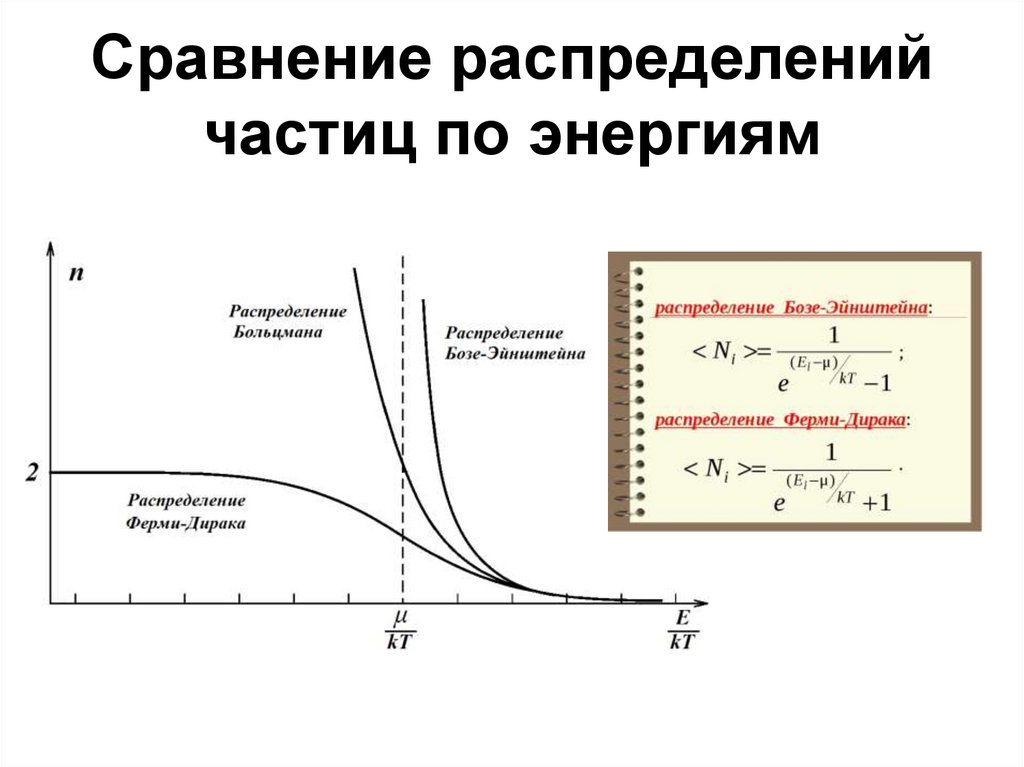
110. Сравнение распределений частиц по энергиям

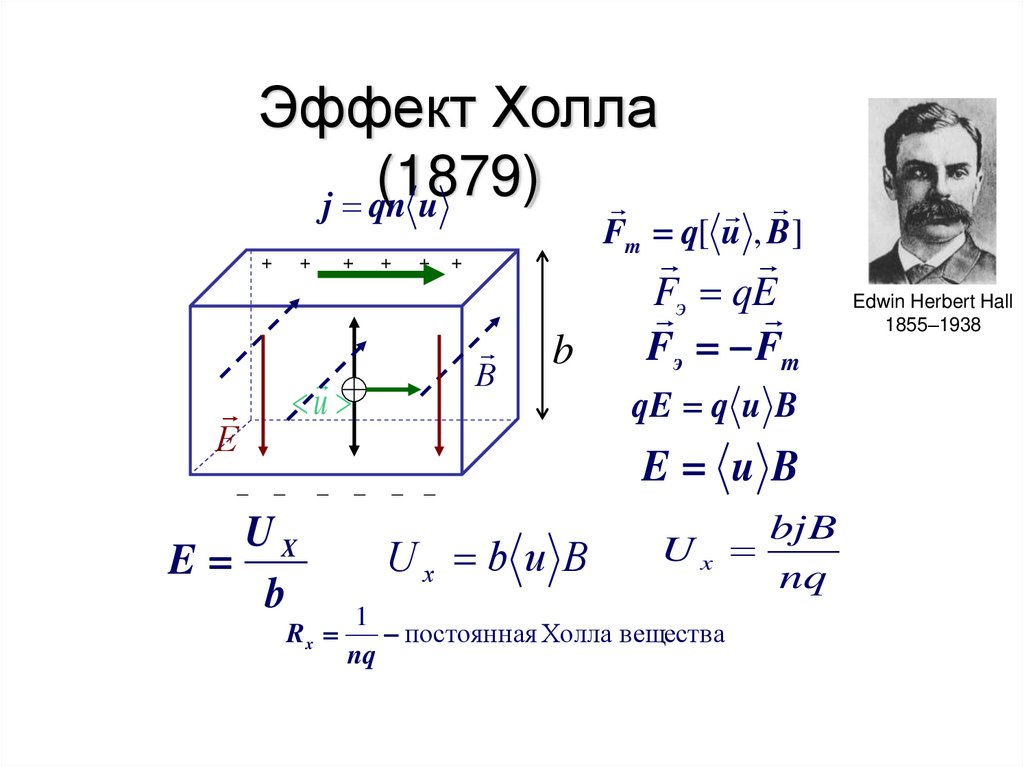
111. Эффект Холла (1879)

j qn u
+
+
Fм
+
+
+
В
u
Е
_
+
Fm q[ u , B ]
b
Fэ
_
_
UX
E
b
Rx
_
_
_
Ux b u B
F
q
E
э
Fэ Fm
qE q u B
E uB
bjB
Ux
nq
1
постоянная Холла вещества
nq
Edwin Herbert Hall
1855–1938

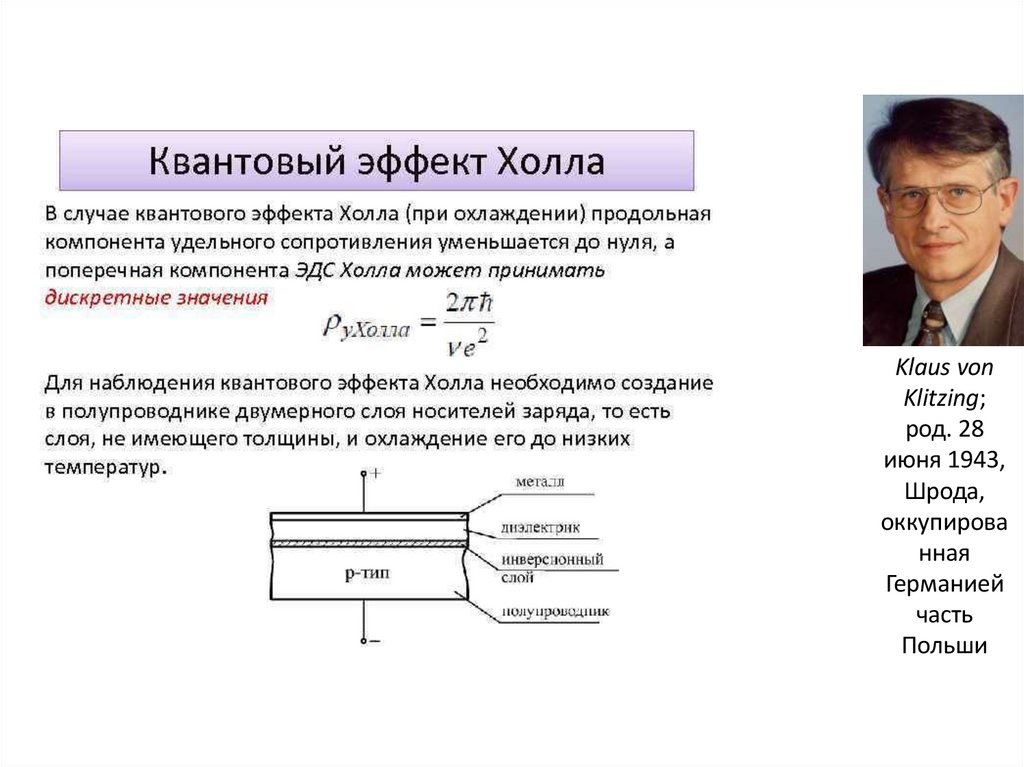
112. Эффект Холла

j qn u
_
u
_
_
_
Fм
Е
+
_
Fm q[ u , B ]
_
В
b
qE q u B
Fэ
+
+
UX
E
b
Rx
F
q
E
э
Fэ Fm
+
+
+
Ux b u B
E uB
bjB
Ux
nq
1
постоянная Холла вещества
nq

113.

Исследования ЭДС Холла привели к
удивительным выводам:
Металлы могут обладать
проводимостью р –типа (Zn, Cd – у них
дырки более подвижные, чем
электроны).
Это металлы с чуть
перекрывающимися зонами, т.е.
полуметаллы.

114. Применение эффекта Холла

Применен
ие
эффекта
Холла
Hall

115.

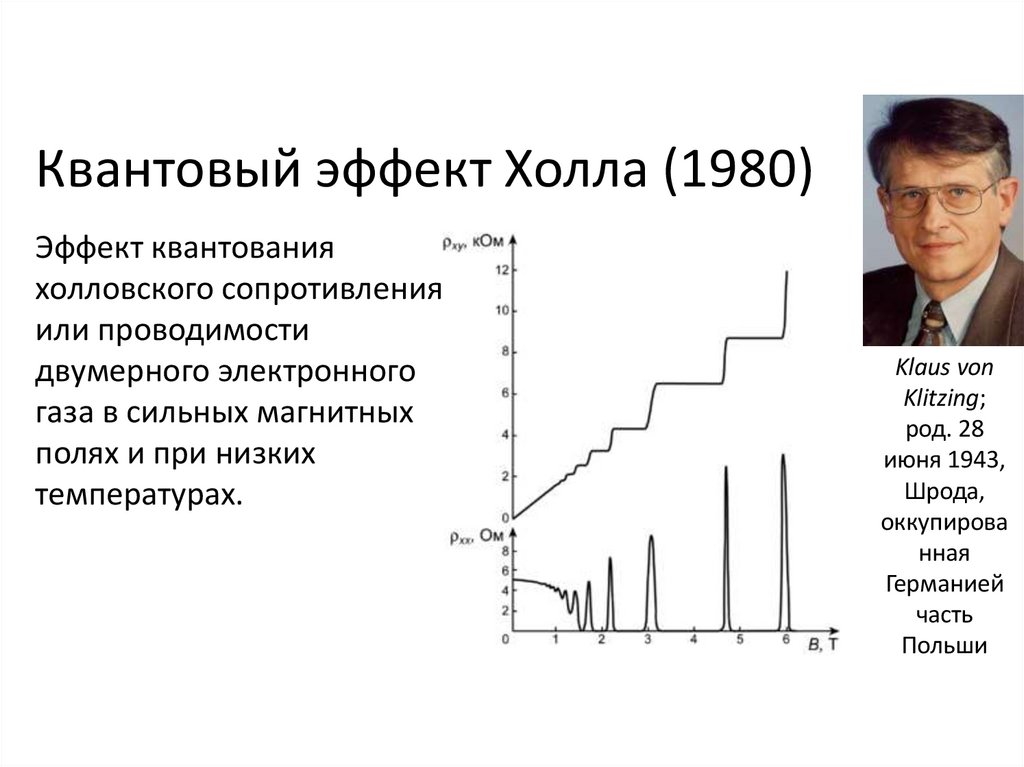
Квантовый эффект Холла (1980)
Эффект квантования
холловского сопротивления
или проводимости
двумерного электронного
газа в сильных магнитных
полях и при низких
температурах.
Klaus von
Klitzing;
род. 28
июня 1943,
Шрода,
оккупирова
нная
Германией
часть
Польши

116.

Klaus von
Klitzing;
род. 28
июня 1943,
Шрода,
оккупирова
нная
Германией
часть
Польши

117.

118.

119. Современные методы исследования состава и структуры вещества

119

120.

Электронный
парамагнитный
резонанс
120

121. Общий магнитный момент атома равен векторной сумме магнитных моментов (орбитальных и спиновых) всех электронов:

Pa Pm PmS

122.

Общий орбитальный момент атома в магнитном поле равен
векторной сумме:
Pm Pmi ΔPmi
магнитный
Тогда орбитальный момент атома
2
e ZS
Pm
B
4πm
Z – число электронов в атоме

123.

124.

В магнитном поле векторы L и P , и сама орбита
e
m
прецессирует вокруг направления вектора
В
Эта прецессия называется
Ларморовской прецессией.
Угловая скорость этой прецессии
ωL зависит только от индукции
магнитного поля В и совпадает с ней
по направлению:
e
ωL
B
2m

125.

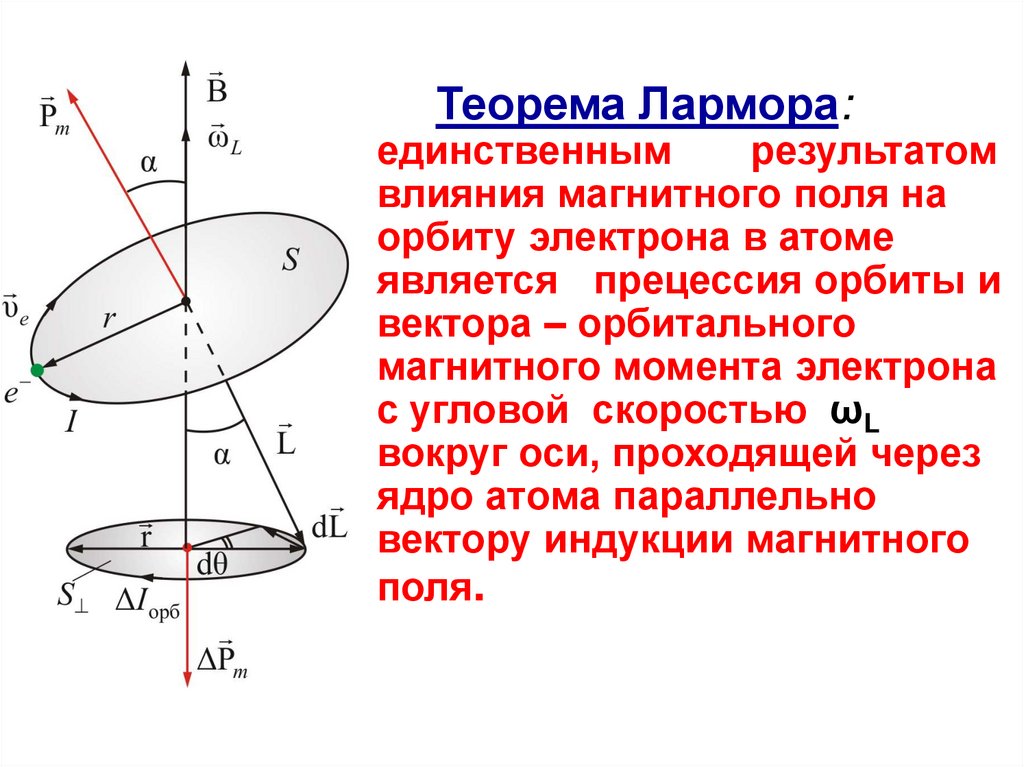
Теорема Лармора:
единственным
результатом
влияния магнитного поля на
орбиту электрона в атоме
является прецессия орбиты и
вектора – орбитального
магнитного момента электрона
с угловой скоростью ωL
вокруг оси, проходящей через
ядро атома параллельно
вектору индукции магнитного
поля.

126.

Прецессия орбиты электрона в
атоме приводит к появлению
дополнительного орбитального
тока, направленного противоположно
току I
ωL
ΔI орб e
2π
и соответствующего ему
наведенного орбитального магнитного
момента ΔPm
e2 S
ΔP m ΔI орб S
B
4πm
,где S – площадь проекции орбиты электрона
на плоскость, перпендикулярную вектору
В .
Знак минус говорит, что Δ Pm
противоположен вектору В .

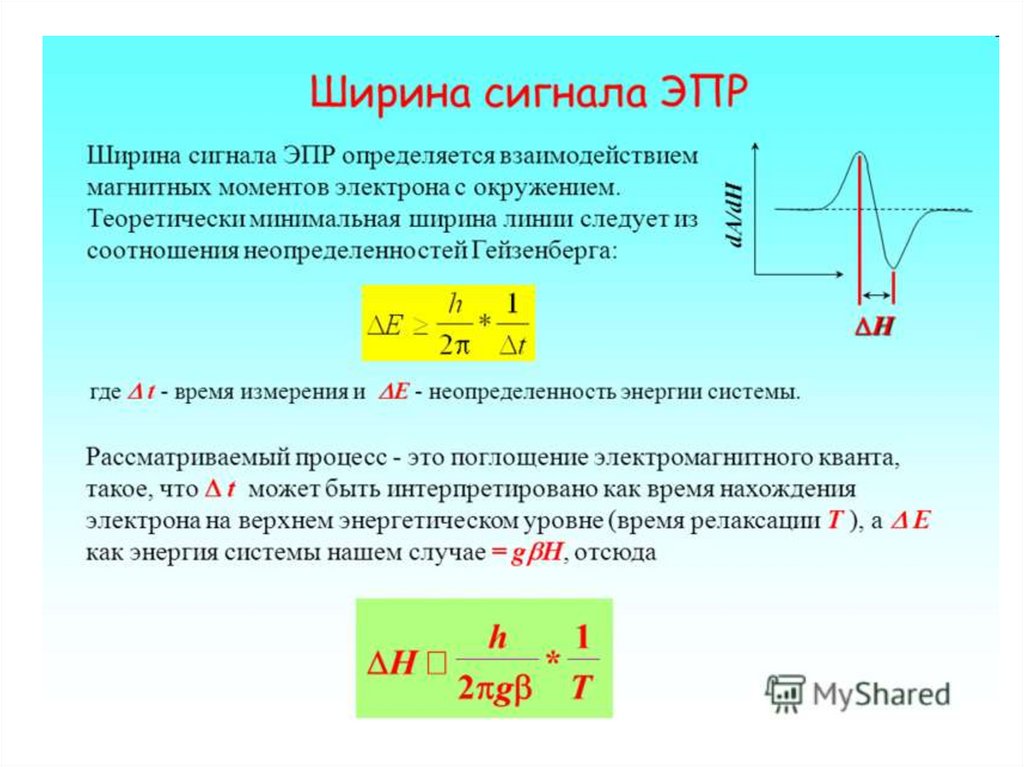
127. В магнитном поле, спин-орбитальное взаимодействие приводит к расщеплению энергетических уровней

μs
sz Б
I
Вэф
E -( s Bэф )
E ls -( sz Bl ) Б Вl
E En Б Bl

128.

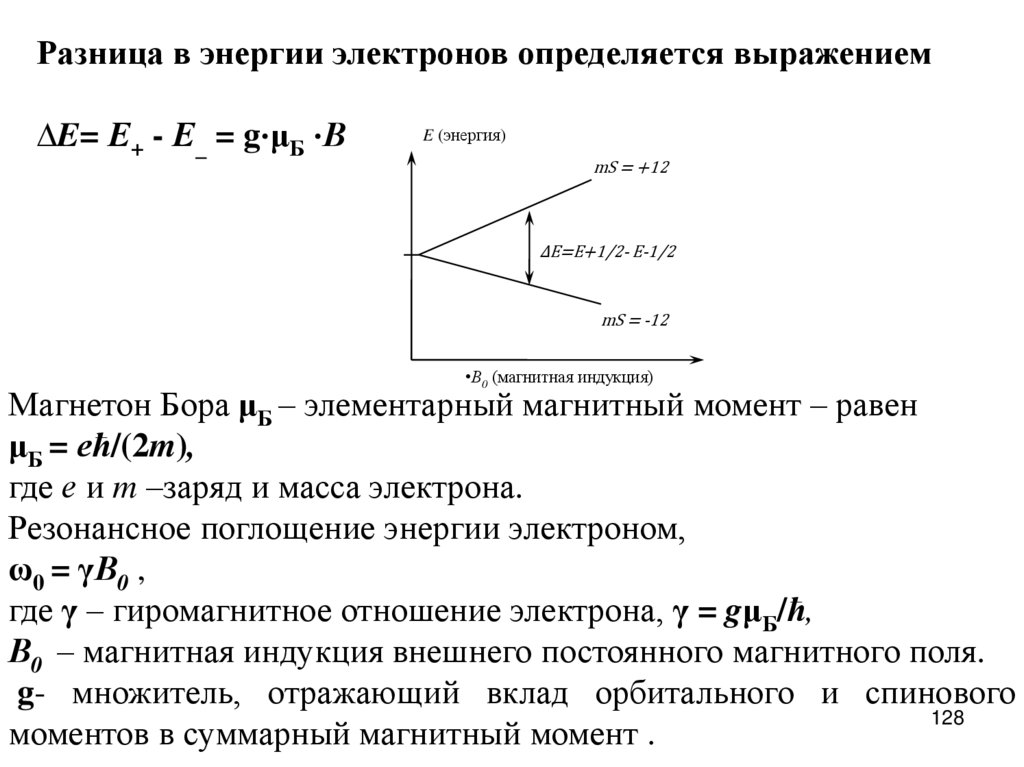
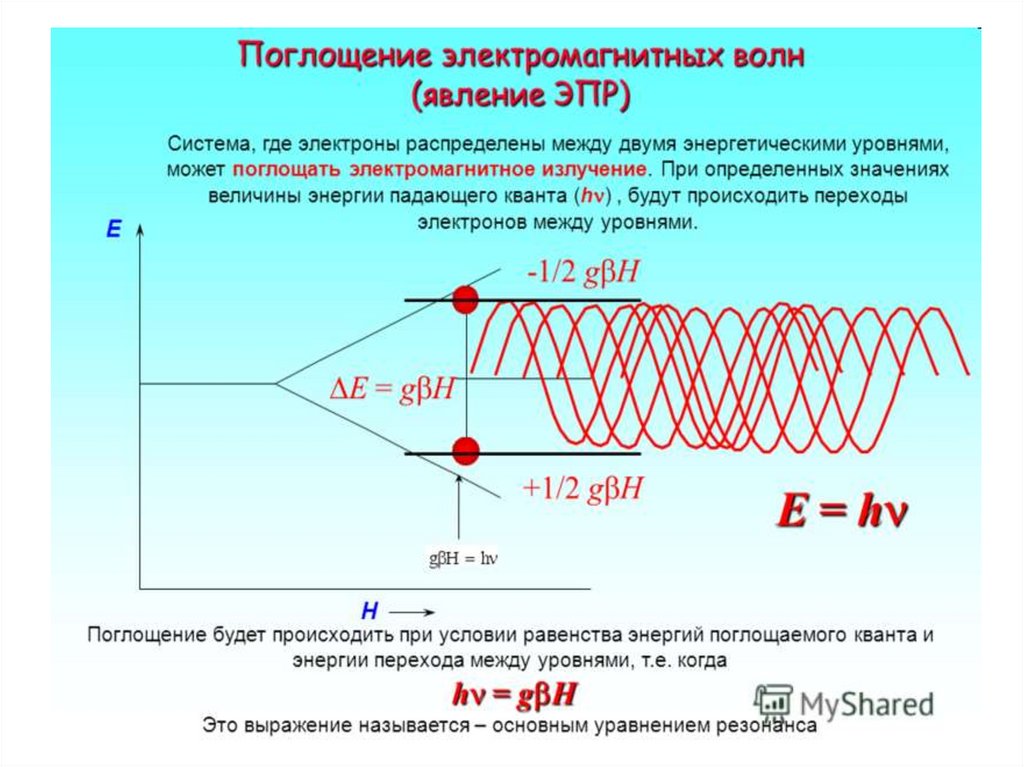
Разница в энергии электронов определяется выражением
∆E= Е+ - Е_ = g⋅μБ ⋅В
E (энергия)
mS = +12
∆E=E+1/2- E-1/2
mS = -12
•В0 (магнитная индукция)
Магнетон Бора μБ – элементарный магнитный момент – равен
μБ = ећ/(2m),
где е и m –заряд и масса электрона.
Резонансное поглощение энергии электроном,
ω0 = γВ0 ,
где γ – гиромагнитное отношение электрона, γ = gμБ/ћ,
В0 – магнитная индукция внешнего постоянного магнитного поля.
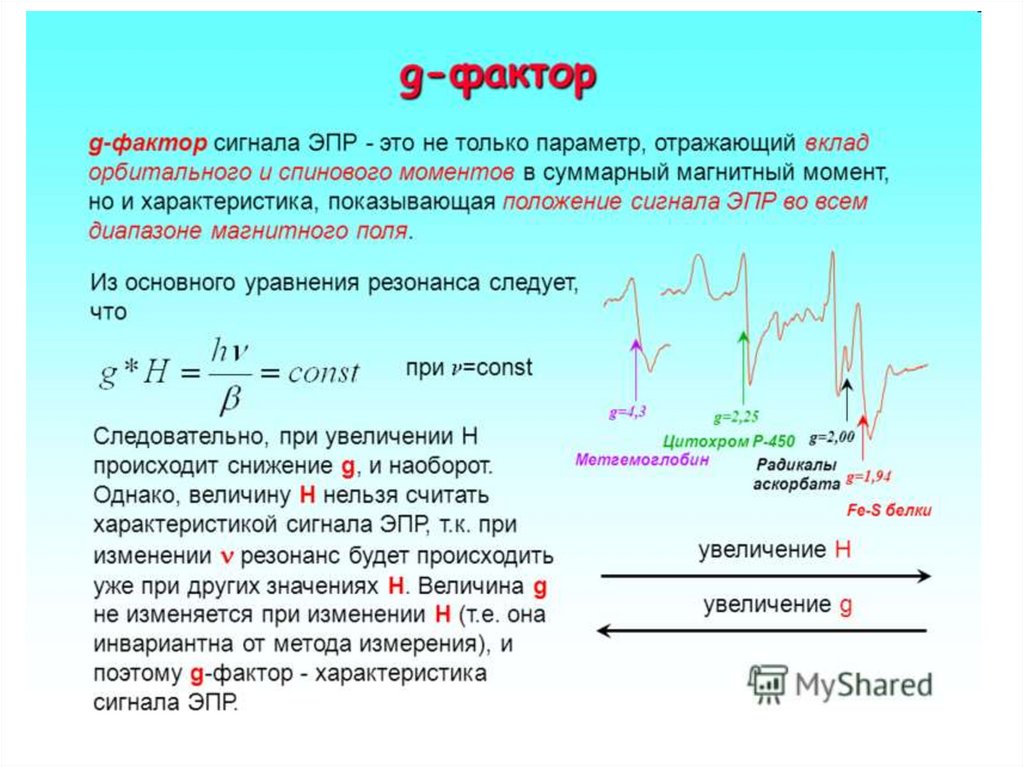
g- множитель, отражающий вклад орбитального и спинового
128
моментов в суммарный магнитный момент .

129.

130.

131.

132.

133.

134.

135.

136.

137.

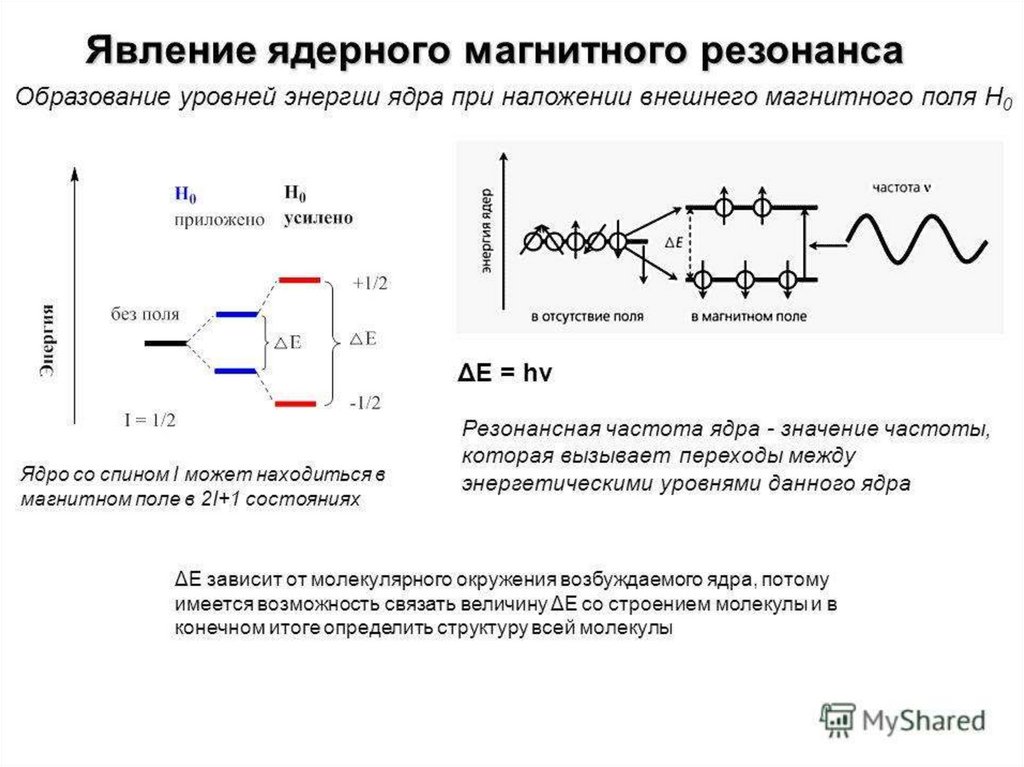
137

138. Ядерный магнитный резонанс

В основе явления ядерного магнитного резонанса лежат магнитные
свойства атомных ядер, состоящих из нуклонов с полуцелым
спином 1/2, 3/2, 5/2…. Ядра с чётными массовым и зарядовым
числами (чётно-чётные ядра) не обладают магнитным моментом, в
то время как для всех прочих ядер магнитный момент отличен от
нуля.
Таким образом, ядра обладают моментом количества движения
связанным с магнитным моментом
соотношением
где
— постоянная Планка,
— спиновое квантовое число,
— гиромагнитное отношение

139.

Момент количества движения и магнитный момент ядра
квантованы, и собственные значения проекции и момента
количества движения и магнитного моментов на ось z произвольно
выбранной системы координат определяются соотношением
и
, где
— магнитное квантовое число собственного состояния
ядра, его значения определяются спиновым квантовым
числом ядра
состояниях.
то есть ядро может находиться в
может находиться только в двух
Так, у протона
состояниях

140.

Ядро можно представить как магнитный диполь, z-компонента
которого может быть ориентирована параллельно либо
антипараллельно положительному направлению оси z произвольной
системы координат.
Следует отметить, что в отсутствие внешнего магнитного поля все
состояния с различными μz имеют одинаковую энергию, то есть
являются вырожденными. Вырождение снимается во внешнем
магнитном поле, при этом расщепление относительно
вырожденного состояния пропорционально величине внешнего
магнитного поля и магнитного момента состояния и для ядра со
спиновым квантовым числом I во внешнем магнитном поле
появляется система из 2I+1 энергетических уровней

141.

В простейшем случае для ядра со спином с I = 1/2 — например, для
протона, расщепление
и разность энергии спиновых состояний
ЯМР-томография впервые в мире изобретены в 1960 г. В. А. Ивановым.[5][6] Заявку на
изобретение (способ и устройство) некомпетентный эксперт отклонил «… ввиду явной
бесполезности предлагаемого решения», поэтому авторское свидетельство на это было
выдано лишь более чем через 10 лет. Таким образом, официально признано, что автором
ЯМР-томографии является не коллектив нижеуказанных нобелевских лауреатов, а
российский учёный. Невзирая на этот юридический факт, Нобелевская премия была
присуждена за ЯМР-томографию вовсе не В. А. Иванову.

142.

142

143.

143

144.

144

145.

145

146. Ядерный гамма- резонанс.

Ядерный гамма-резонанс (Эффект Мёссбауэра)
состоит в резонансном испускании или поглощении
гамма-фотонов без изменения фононного спектра
излучателя или поглотителя излучения
соответственно. Иными словами, эффект
Мёссбауэра — это резонансное испускание и
поглощение гамма-лучей без отдачи. Имеет
существенно квантовую природу и наблюдается при
изучении кристаллических, аморфных и порошковых
образцов, содержащих один из 87 изотопов 46
элементов.

147. Ядерный гамма резонанс

Пусть имеются два одинаковых первоначально
покоящихся ядра, одно из которых находится в основном
состоянииЕ1, другое — в возбужденном с энергией
возбуждения Е2. Переходя в основное состояние,
возбужденное ядро испускает γ-квант с энергией ħω0 и
импульсом ħω0 / с , удовлетворяющим законам
сохранения:
ħω =Е - Е
0
2
1
ħωисп= ħω - К
0
ħωпогл= ħω0+ К
где К — энергия отдачи ядра.
здесь т — масса ядра.

148.

Согласно первой формуле энергия γ-кванта ħω изменяется
относительно энергии Е ядерного перехода на величину К —
энергию отдачи ядра. Поэтому γ-квант сможет поглотиться другим
ядром только при условии, что это изменение
где Г — ширина возбужденного
уровня Е.
57
Насколько выполняется это соотношение. Например, ядро Fe
при переходе из первого возбужденного состояния испускает γквант с энергией ħω ≈ 14 кэВ. При этом его энергия испытывает
сдвиг на величину
Ширина же Г первого возбужденного уровня, время жизни которого
τ ~ 10-7 с, согласно соотношению неопределенностей ∆Е ·∆t ~ ħ
равна
Таким образом, сдвиг К не меньше Г, а наоборот, больше на пять
порядков, что далеко перекрывает возможность резонансного
поглощения.

149. Ядерная гамма-резонансная спектроскопия.

Метод ядерного гамма-резонанса основан на
эффекте резонансного поглощения без отдачи
атомным ядром монохроматического γ-излучения,
испускаемого радиоактивным источником. В
абсорбционной мёссбауэровской спектроскопии
образец-поглотитель просвечивается гаммаквантами, излучаемыми возбуждённым железом-57
(57Fe), иридием-191 (191Ir) или другим
мёссбауэровским изотопом. Возбуждённые ядра в
источнике создаются при распаде соответствующего
радиоактивного изотопа (например, 57Co,
превращающийся в возбуждённое состояние 57Fe).

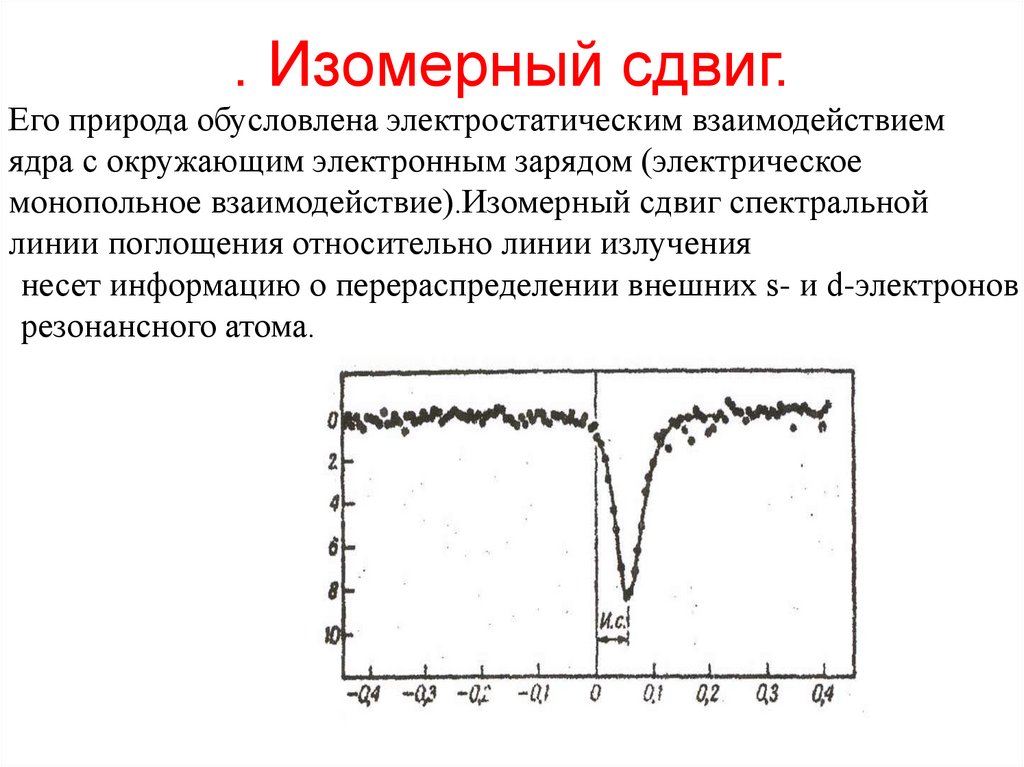
150. . Изомерный сдвиг.

Его природа обусловлена электростатическим взаимодействием
ядра с окружающим электронным зарядом (электрическое
монопольное взаимодействие).Изомерный сдвиг спектральной
линии поглощения относительно линии излучения
несет информацию о перераспределении внешних s- и d-электронов
резонансного атома.

151. Квадрупольное расщепление.

Ядра со спином 0 и 1/2 имеют сферически-симметричную
форму. Их электрический квадрупольный момент
вследствие этого равен нулю.
Ядра со спином I > 1/2 не обладают сферической
симметрией и характеризуются квадрупольным моментом
Q, отличным от нуля.
Взаимодействие квадрупольного момента с градиентом
электрического поля приводит к частичному снятию
вырождения по магнитному квантовому числу и
расщеплению уровней ядра на подуровни .

152.

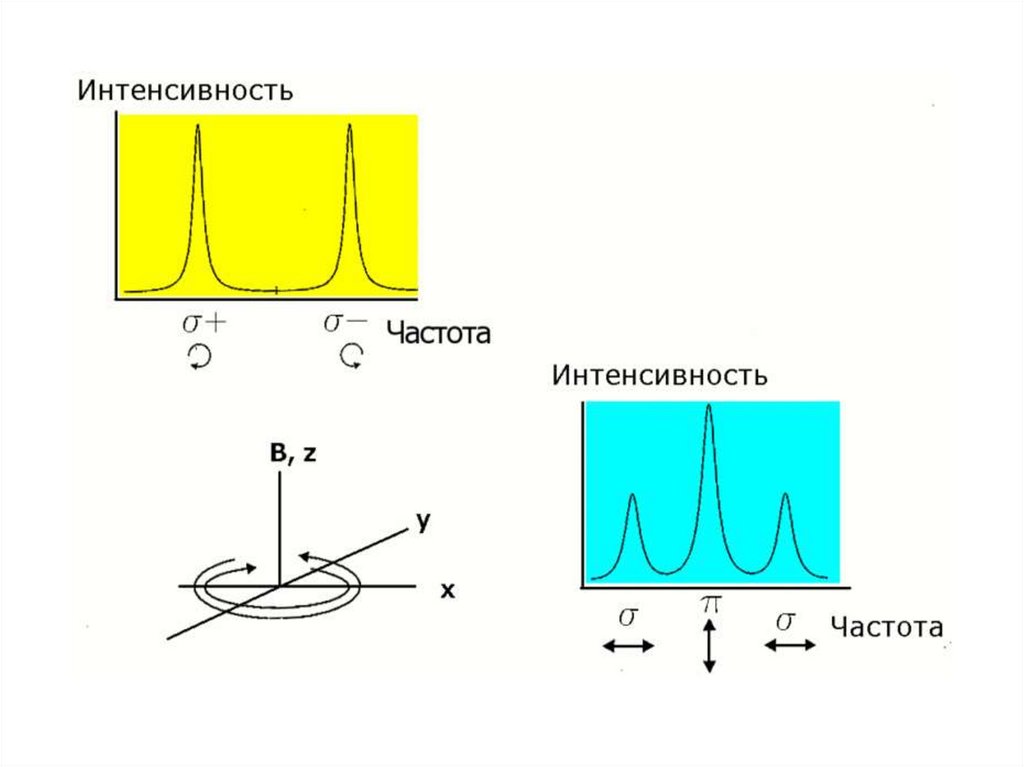
153. Эффект Зеемана.

Эффект Зеемана — расщепление линий атомных
спектров в магнитном поле.
Эффект обусловлен тем, что в присутствии
магнитного поля квантовая частица, обладающая
спиновым магнитным моментом, приобретает
дополнительную энергию,пропорциональную его
магнитному моменту.
Приобретённая энергия приводит к снятию
вырождения атомных состояний по магнитному
квантовому числу и расщеплению атомных линий:

154.

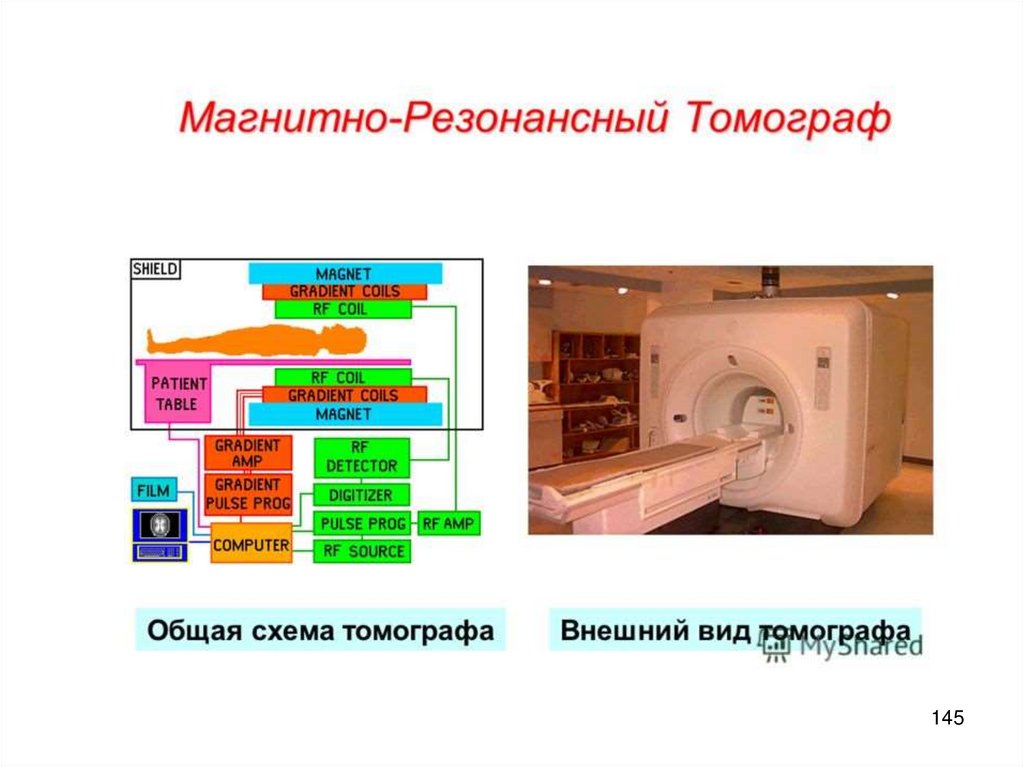
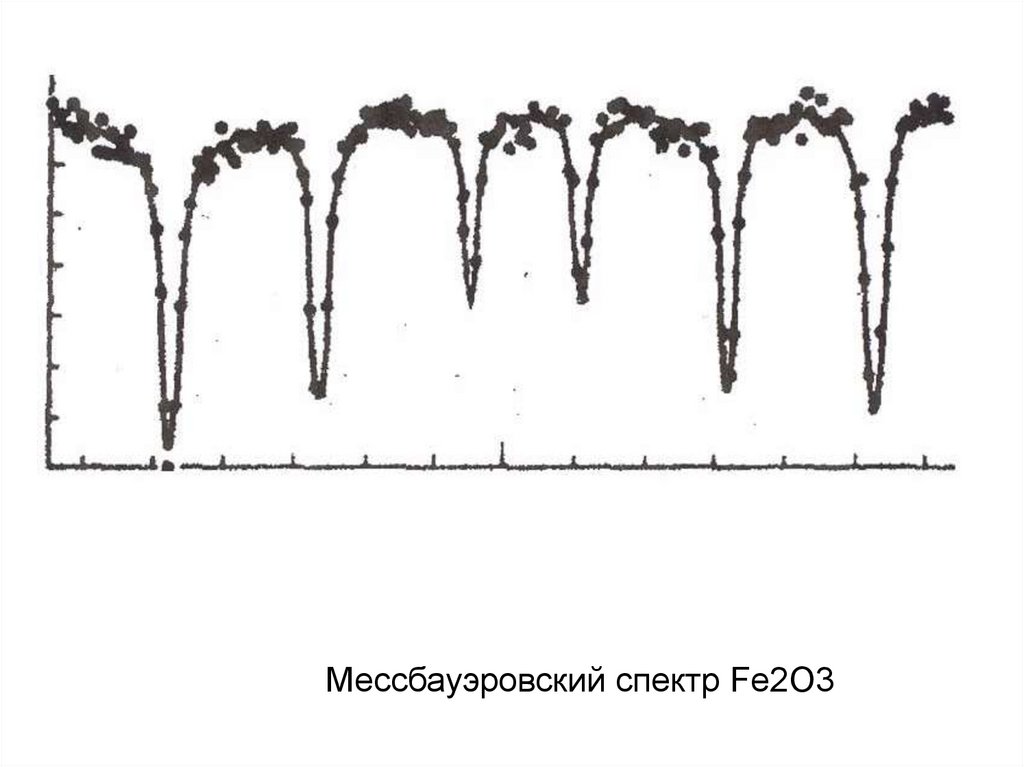
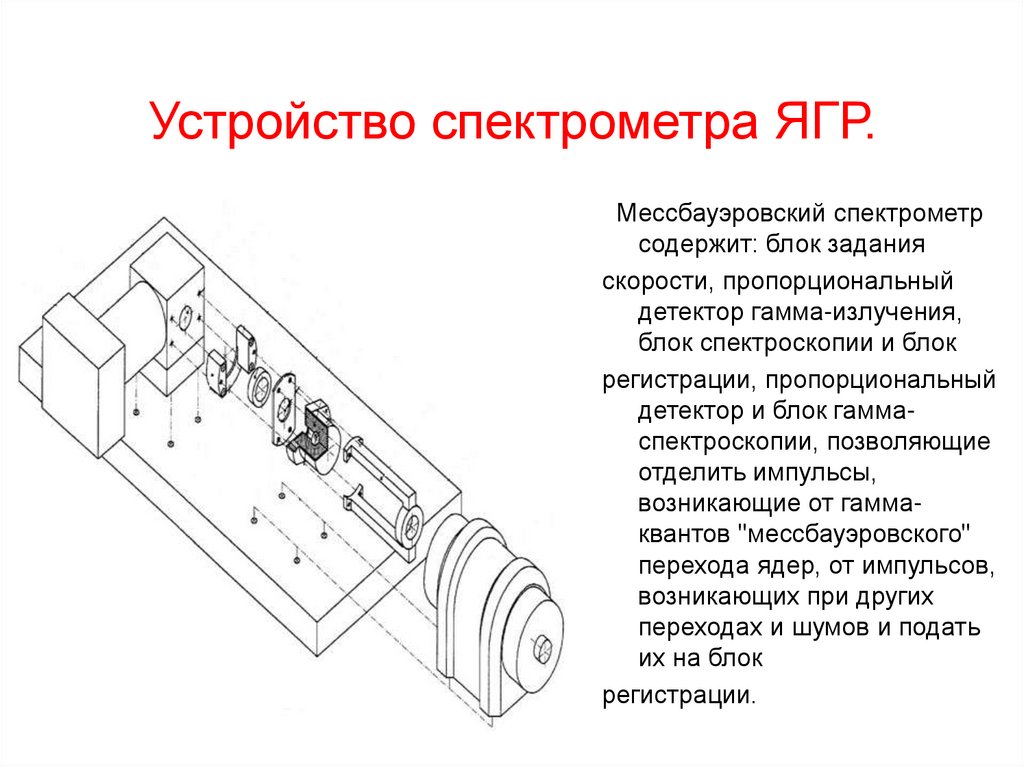
Мессбауэровский спектр Fe2O3

155. Устройство спектрометра ЯГР.

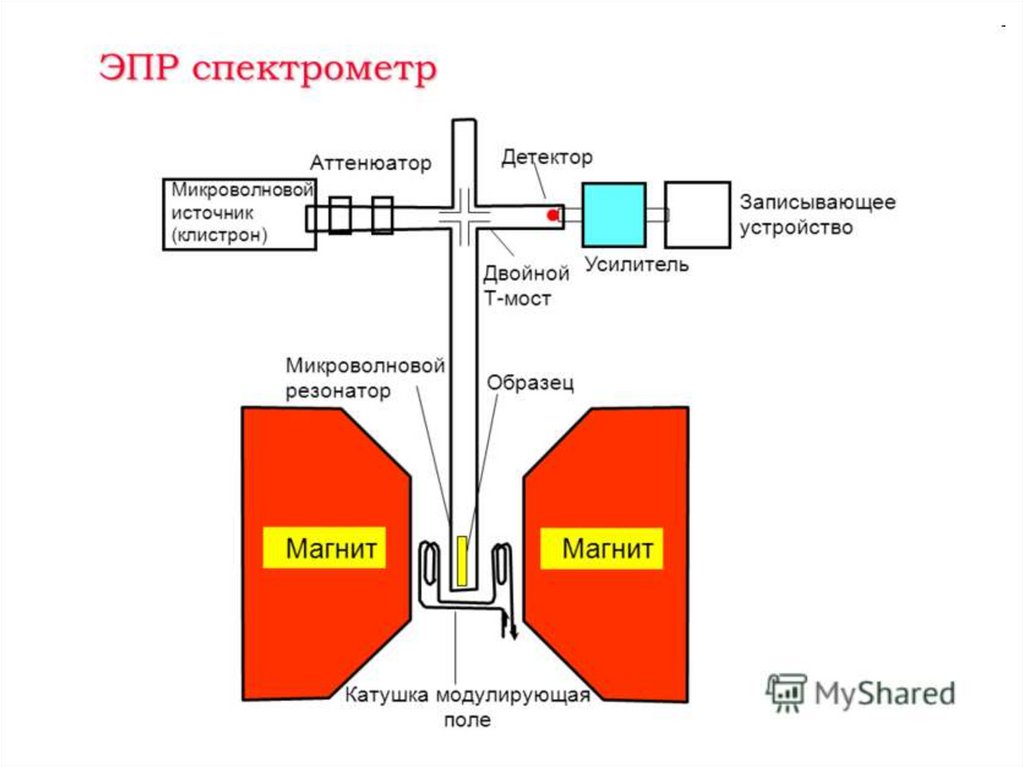
Мессбауэровский спектрометр
содержит: блок задания
скорости, пропорциональный
детектор гамма-излучения,
блок спектроскопии и блок
регистрации, пропорциональный
детектор и блок гаммаспектроскопии, позволяющие
отделить импульсы,
возникающие от гаммаквантов "мессбауэровского"
перехода ядер, от импульсов,
возникающих при других
переходах и шумов и подать
их на блок
регистрации.

156.

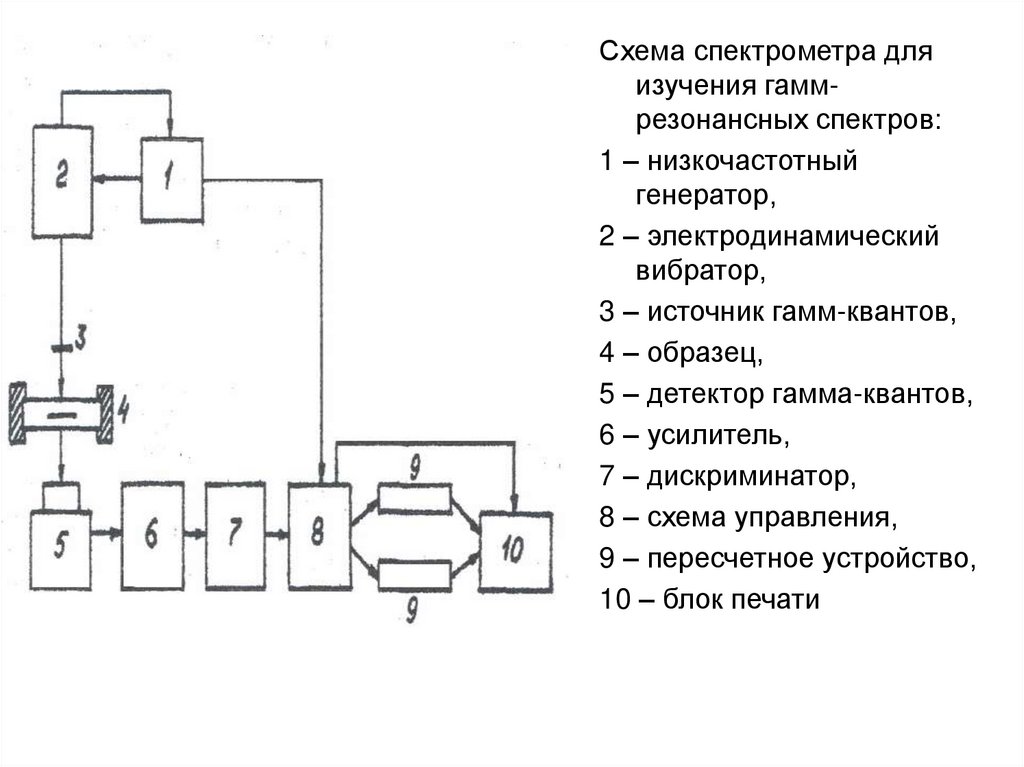
Схема спектрометра для
изучения гаммрезонансных спектров:
1 – низкочастотный
генератор,
2 – электродинамический
вибратор,
3 – источник гамм-квантов,
4 – образец,
5 – детектор гамма-квантов,
6 – усилитель,
7 – дискриминатор,
8 – схема управления,
9 – пересчетное устройство,
10 – блок печати

157.

Мессбауэровский спектрометр МС1104Ем
с источником Co57 (Cr) позволяет
проводить исследования спектров
ядерного гамма-резонанса на ионах
железа. Диапазон скоростей ±80 мм/с,
нелинейность скорости не более
±0.05%, отклонение нулевой скорости
не более ±3 мкм/с. Спектрометр
имеет два канала регистрации с
резонансным сцинтилляционным
детектором, который увеличивает
скорость накопления спектра и
разрешающую способность
спектрометра. Каждый канал
регистрации имеет 1024 канала
накопления импульсов с емкостью
канала 232. Диапазон температур 70–
300 К. С помощью мессбауэровской
спектроскопии исследуется состояние
железа и его распределение по
позициям кристаллических решеток, в
частности: продукты твердофазного
синтеза, структурные и магнитные
превращения, фазовый состав
железо-содержащих соединений и
структур различной природы.