Системы счисления

1. Системы счисления

Тема занятия:
СИСТЕМЫ
СЧИСЛЕНИЯ

2.

На ранних ступенях развития общества
люди почти не умели считать. Они различали
совокупности двух и трех предметов; всякая
совокупность, содержавшая бóльшее число
предметов, объединялась в понятии
«много».
Предметы при счете сопоставлялись обычно с пальцами рук и ног.
По мере развития цивилизации потребность человека в счете стала необходимой. Первоначально натуральные числа изображались с помощью некоторого
количества черточек или палочек, затем для их изображения стали использовать буквы или специальные
знаки.

3. Число — это абстрактная мера количества. Цифра — это знак для записи числа.

ЧИСЛО — ЭТО АБСТРАКТНАЯ МЕРА
КОЛИЧЕСТВА.
ЦИФРА — ЭТО ЗНАК ДЛЯ ЗАПИСИ
ЧИСЛА.
Система счисления (СС)
– это способ записи чисел с помощью
цифр и правила действий над ними

4. Системы счисления бывают:

Смешанные
Непозиционные
(аддитивные)
Позиционные
(мультипликативные)

5. Денежные знаки - это пример смешанной системы счисления

ДЕНЕЖНЫЕ ЗНАКИ - ЭТО ПРИМЕР СМЕШАННОЙ
СИСТЕМЫ СЧИСЛЕНИЯ

6. Непозиционная система счисления

НЕПОЗИЦИОННАЯ СИСТЕМА СЧИСЛЕНИЯ
Непозиционная система счисления -
система счисления, в которой для
обозначения чисел вводятся
специальные знаки, количественное
значение которых всегда одинаково и не
зависит от их места в записи числа.
Например:
- это число 261

7. Непозиционные системы счисления

Единичная или унарная СС (период палеолита
– 10-11 тысяч лет до н. э.)
Древнеегипетская десятичная СС (вторая
половина 3 тысячелетия до н. э.)
Римская СС (более 2500 лет назад в
Древнем Риме)
Греческая СС (ионийская, славянская,
кириллическая, финикийская)
Древнеиндийские СС (VI в. до н. э. – III в. н. э.)

8. Древнеегипетская десятичная система счисления

ДРЕВНЕЕГИПЕТСКАЯ ДЕСЯТИЧНАЯ СИСТЕМА
СЧИСЛЕНИЯ
1. Как и большинство людей для счета небольшого количества предметов
Египтяне использовали палочки.
10. Такими путами египтяне связывали коров (дуга)
100. Это мерная веревка, которой измеряли земельные участки после
разлива Нила.
1 000 – цветок лотоса
10 000. "В больших числах будь внимателен!" - говорит поднятый вверх
указательный палец.
1 000 000. Увидев такое число, обычный человек очень удивится и
возденет руки к небу. Это и изображает этот иероглиф
10 000 000. Египтяне поклонялись Амону Ра, богу Солнца, и, наверное,
поэтому самое большое свое число они изобразили в виде восходящего
солнца
- 1205
- 1 023 029

9. Римская пятеричная система счисления

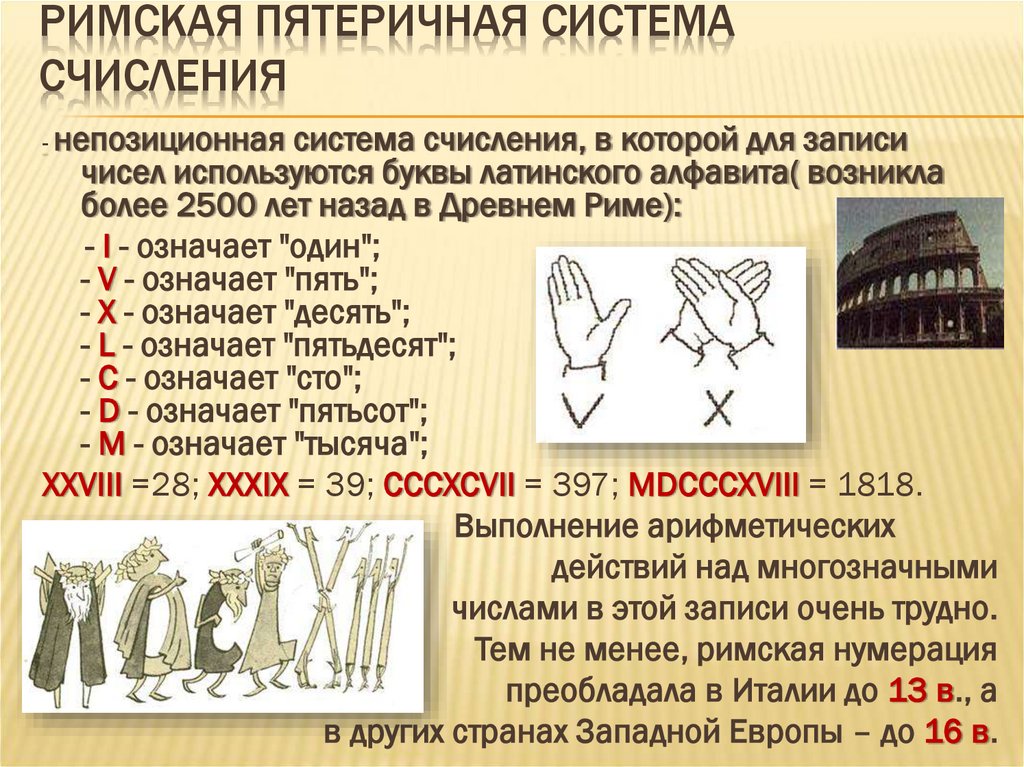
РИМСКАЯ ПЯТЕРИЧНАЯ СИСТЕМА
СЧИСЛЕНИЯ
- непозиционная система счисления, в которой для записи
чисел используются буквы латинского алфавита( возникла
более 2500 лет назад в Древнем Риме):
- I - означает "один";
- V - означает "пять";
- X - означает "десять";
- L - означает "пятьдесят";
- C - означает "сто";
- D - означает "пятьсот";
- M - означает "тысяча";
XXVIII =28; ХХХIХ = 39; CCCXCVII = 397; MDCCCXVIII = 1818.
Выполнение арифметических
действий над многозначными
числами в этой записи очень трудно.
Тем не менее, римская нумерация
преобладала в Италии до 13 в., а
в других странах Западной Европы – до 16 в.

10.

Название происходит от области Греции – Аттики со столицей
Афины. В этой системе числа 1, 2, 3, 4 изображались
соответствующим количеством вертикальных полосок:
Число 10 обозначалось
заглавной "Дельта" от
слова "дека" -"десять".
Н – сто;
Х – тысяча ( по первым буквам слов числительных)

11. Древнегреческая ионийская десятичная алфавитная система счисления

ДРЕВНЕГРЕЧЕСКАЯ ИОНИЙСКАЯ
ДЕСЯТИЧНАЯ АЛФАВИТНАЯ СИСТЕМА
СЧИСЛЕНИЯ
Возникла в Милеете (греческая малоазиатская колония Ионии).
В ней числа 1 - 9 обозначаются первыми буквами древнегреческого алфавита:
Для отличия цифр и букв писали черточки над
цифрами.

12.

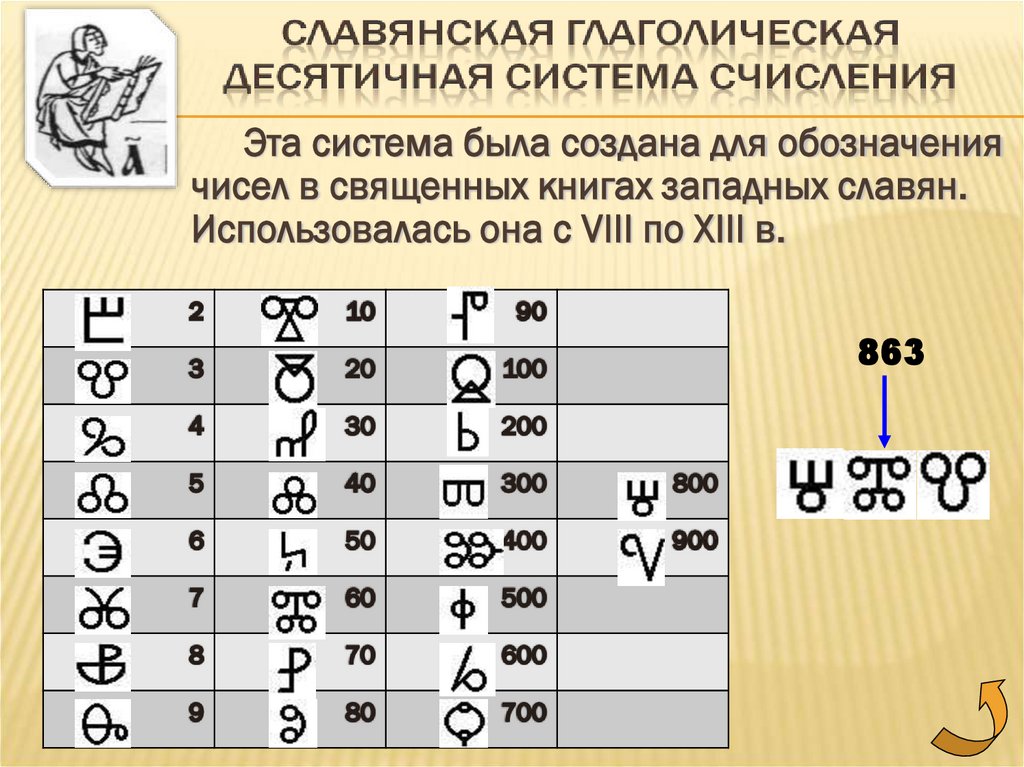
Эта система была создана для обозначения
чисел в священных книгах западных славян.
Использовалась она с VIII по XIII в.
863

13.

Тысяча
1000
Тьма
10 000
Легион
100 000
Леодр
1 000 000
Ворон
Славянская нумерация
просуществовала до конца XVII столетия.
Колода
10 000
000
100 000
000

14. Древнеиндийские системы счисления

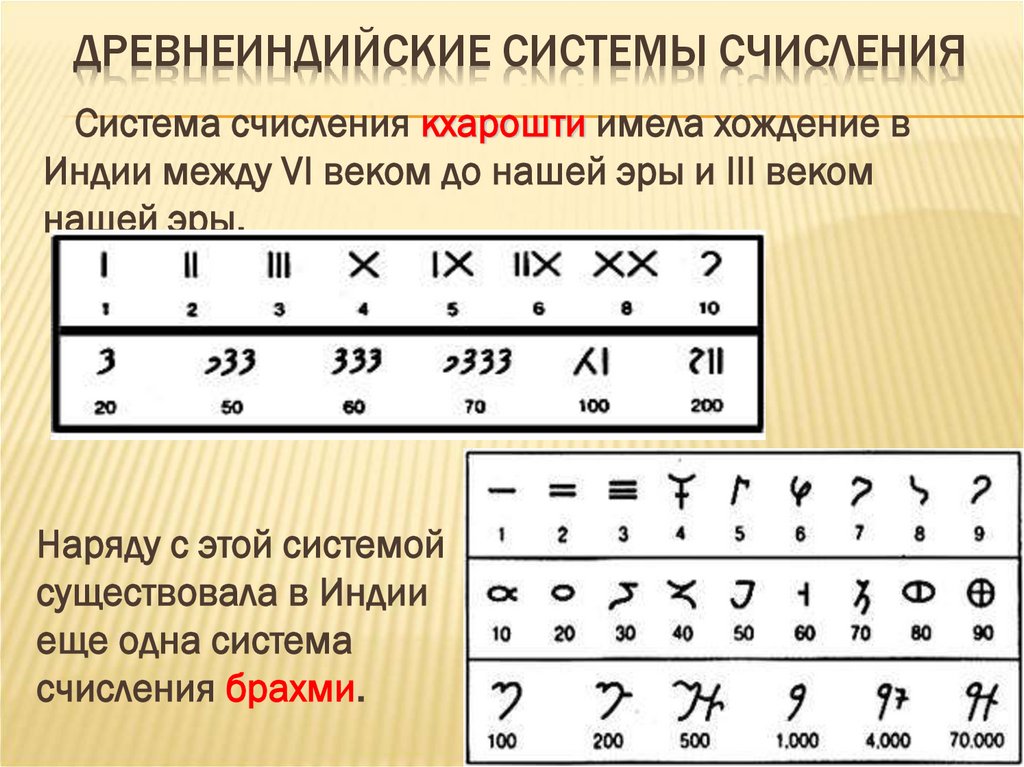
ДРЕВНЕИНДИЙСКИЕ СИСТЕМЫ СЧИСЛЕНИЯ
Система счисления кхарошти имела хождение в
Индии между VI веком до нашей эры и III веком
нашей эры.
Наряду с этой системой
существовала в Индии
еще одна система
счисления брахми.

15. Недостатки непозиционной системы счисления

НЕДОСТАТКИ НЕПОЗИЦИОННОЙ СИСТЕМЫ
СЧИСЛЕНИЯ
1.
2.
3.
Существует постоянная потребность
введения новых знаков для записи
больших чисел.
Трудно представлять дробные и
отрицательные числа.
Сложно выполнять арифметические
операции, так как не существует
алгоритмов их выполнения.

16. Позиционные системы счисления

ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Позиционная система счисления - система
счисления, использующая для записи чисел
ограниченное число знаков, «вес» которых зависит от
места в записи числа.
Место каждой цифры в числе называется
позицией
(разрядом).
Количество цифр используемых в системе счисления
называется основанием (разрядностью) и
обозначается – р.

17.

двоичная система счисления;
система счисления с основанием е=2,718281828;
троичная система счисления;
пятеричная система счисления (у
ряда африканских племен и в
Древнем Китае );
семеричной системе счисления;
восьмеричная система счисления;
двенадцатеричная система счисления;
шестнадцатеричная система счисления;
двадцатеричная система (у древних ацтеков и майя, и
среди населявших Западную Европу древних кельтов) ;
шестидесятеричная (вавилонская) система счисления (00,
01, 02, ..., 59)

18. Интересные факты

ИНТЕРЕСНЫЕ ФАКТЫ
В настоящее время, в полном виде или в виде
следов и остатков прежнего употребления:
5-ричная система счисления употребляется у
26 племен Африки, 8 — Полинезии, 13 — Азии
и 30 — Америки;
20-ричная у 4 племен Африки, 3 —
Полинезии, 18 — Азии, 8 — Америки и 6 —
Европы.

19. Двенадцатеричная система счисления

Следующей после пятеричной возникла
двенадцатеричная система счисления. Возникла
она в древнем Шумере. Некоторые учёные
полагают, что такая система возникала у них из
подсчёта фаланг на руке большим пальцем.
Широкое распространение получила двенадцатеричная система
счисления в XIX веке. На ее широкое использование в прошлом
явно указывают названия числительных во многих языках, а
также сохранившиеся в ряде стран способы отсчета времени,
денег и соотношения между некоторыми единицами измерения.
Год состоит из 12 месяцев, а половина суток состоит из 12
часов.
Элементом двенадцатеричной системы в современности может
служить счёт дюжинами. Первые три степени числа 12 имеют
собственные названия: 1 дюжина = 12 штук; 1 гросс = 12
дюжин = 144 штуки; 1 масса = 12 гроссов = 144 дюжины =
1728 штук.
Английский фунт состоит из 12 шиллингов.

20.

В древнем Вавилоне примерно во II тысячелетие до
нашей эры была такая система счисления - числа
менее 60 обозначались с помощью двух знаков:
д ля единицы
и
для десятка.
- 3;
- 20;
- 59
- 302
Лишь в V веке до нашей эры был введен особый
знак
- наклонный клин для обозначения
пропущенных разрядов, игравший роль нуля.

21. Древнекитайская десятичная система счисления

ДРЕВНЕКИТАЙСКАЯ ДЕСЯТИЧНАЯ СИСТЕМА
СЧИСЛЕНИЯ
Возникла около 4 000 тысяч лет тому назад в Китае
1
6
2
7
8
3
9
4
5
10
100
1 000
O
0
10 000
5 * 100+4* 10+8 = 548

22. Двадцатеричная система счисления индейцев Майя или долгий счет

.
ДВАДЦАТЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
ИНДЕЙЦЕВ МАЙЯ ИЛИ ДОЛГИЙ СЧЕТ
Эта система применялась для календаря и астрономических
наблюдений. Характерной особенностью ее было наличие
нуля (изображение ракушки). Число 20 изображалось из двух
цифр, ноль и один наверху и называлось уиналу
.
число 21, это будет

23. Операции над числами:

24.

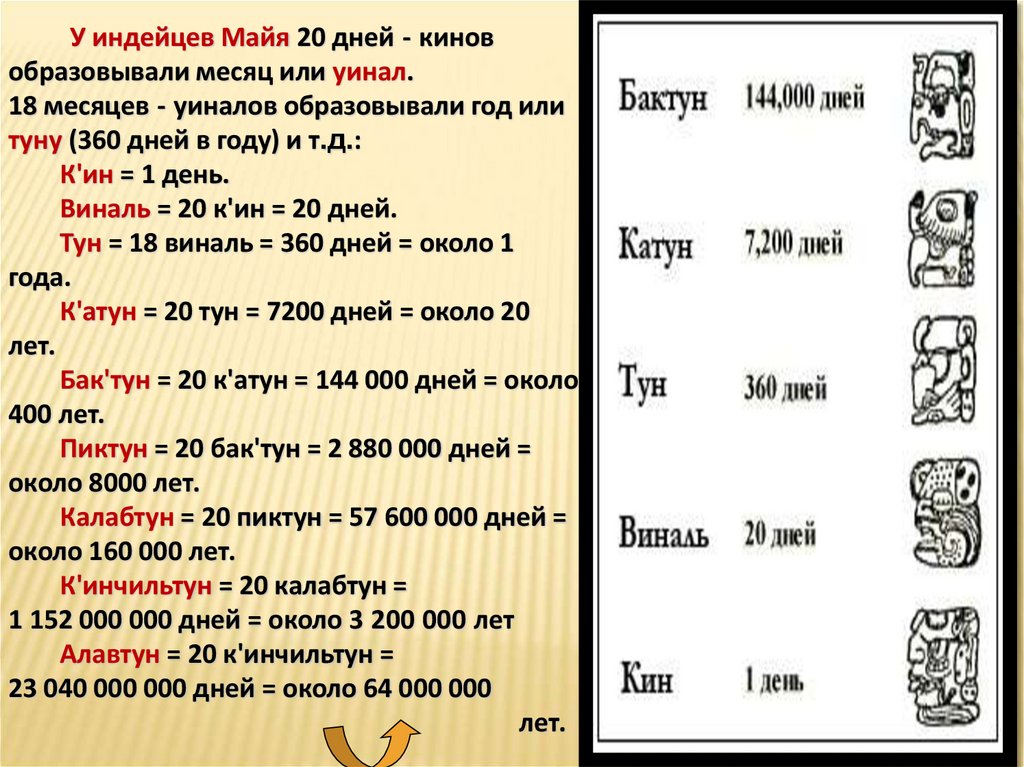
У индейцев Майя 20 дней - кинов
образовывали месяц или уинал.
18 месяцев - уиналов образовывали год или
туну (360 дней в году) и т.д.:
К'ин = 1 день.
Виналь = 20 к'ин = 20 дней.
Тун = 18 виналь = 360 дней = около 1
года.
К'атун = 20 тун = 7200 дней = около 20
лет.
Бак'тун = 20 к'атун = 144 000 дней = около
400 лет.
Пиктун = 20 бак'тун = 2 880 000 дней =
около 8000 лет.
Калабтун = 20 пиктун = 57 600 000 дней =
около 160 000 лет.
К'инчильтун = 20 калабтун =
1 152 000 000 дней = около 3 200 000 лет
Алавтун = 20 к'инчильтун =
23 040 000 000 дней = около 64 000 000
лет.

25.

Более удобной и общепринятой и
наиболее распространенной
является индо - арабская десятичная система счисления,
которая была изобретена в Индии,
заимствована там арабами и затем
через некоторое время пришла в
Европу
(0, 1, 2, 3, 4, 5, 6, 7, 8 и 9).

26. Восьмеричная система счисления

ВОСЬМЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
В восьмеричной (octal) системе счисления
используются восемь различных цифр:
0, 1, 2, 3, 4, 5, 6, 7. Основание системы р = 8.
В различных языках программирования
запись восьмеричных чисел начинается с 0,
например, запись 011 означает число 9.

27. Шестнадцатеричная система счисления

ШЕСТНАДЦАТЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
В шестнадцатеричной (hexadecimal) системе
счисления применяется десять различных цифр и
шесть первых букв латинского алфавита
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
A - 10; B – 11; C – 12; D – 13; E – 14; F - 15
Шестнадцатеричная система
счисления широко используется
при задании различных оттенков
цвета при кодировании
графической информации
(модель RGB).

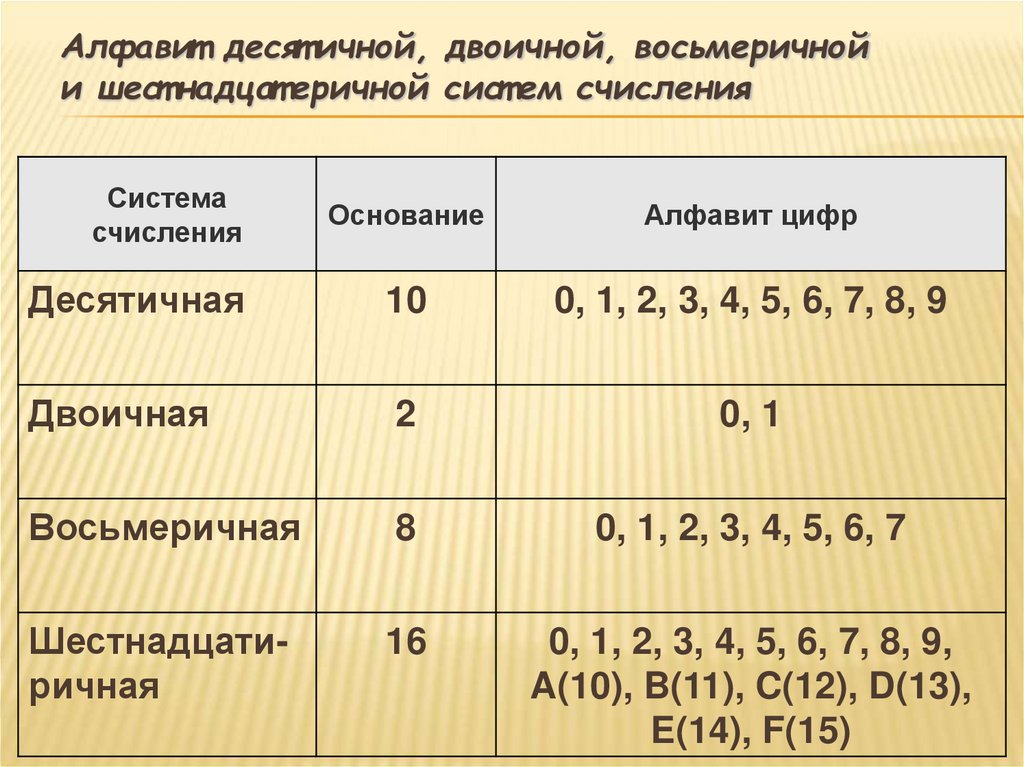
28. Алфавит десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления

Алфавит десят ичной, двоичной, восьмеричной
и шест надцат еричной сист ем счисления
Система
счисления
Основание
Алфавит цифр
Десятичная
10
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двоичная
2
0, 1
Восьмеричная
8
0, 1, 2, 3, 4, 5, 6, 7
Шестнадцатиричная
16
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
A(10), B(11), C(12), D(13),
E(14), F(15)

29. Достоинства позиционных систем счисления

Простота выполнения арифметических
операций
Ограниченное количество символов для
записи числа
Удобна для механического представления
чисел

30. Развёрнутая форма записи числа

В позиционной СС любое целое число может быть
представлено в виде:
Ар = ± (a0р0 + a1р1 + a2р2 +…+ an-2рn-2 + an-1·рn-1 ),
где А – само число,
р – основание СС,
аi – цифры данного числа,
n – число разрядов целой части числа
Например:
1 пример:
А8 = 75648= 4·80 + 6·81 + 5·82 + 7·83 = 4+ 48+ 320+ 3584 =
395610
Разряд
3210
Таким способом можно перевести число из любой СС в
десятичную СС.
2 пример:
100112 = 1·20 + 1·21 + 0·22+0·23+1·24 = 1 + 2 + 0 + 0 + 16 = 1910
Разряд 4 3 2 1 0

31.

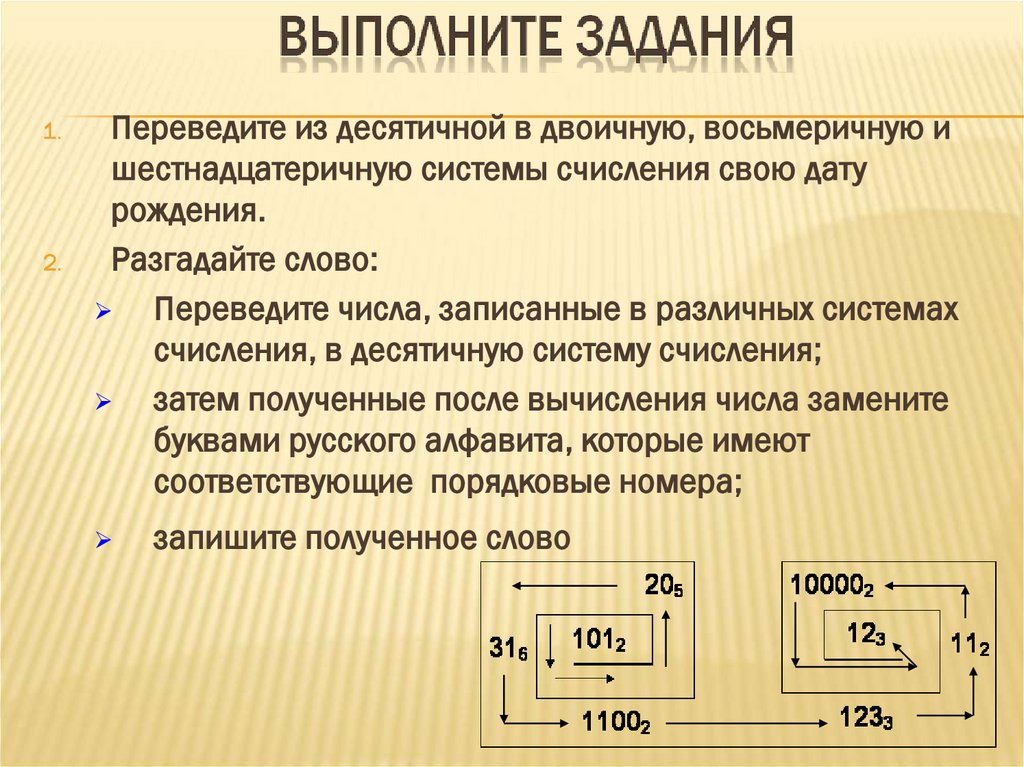
1.
2.
Переведите из десятичной в двоичную, восьмеричную и
шестнадцатеричную системы счисления свою дату
рождения.
Разгадайте слово:
Переведите числа, записанные в различных системах
счисления, в десятичную систему счисления;
затем полученные после вычисления числа замените
буквами русского алфавита, которые имеют
соответствующие порядковые номера;
запишите полученное слово

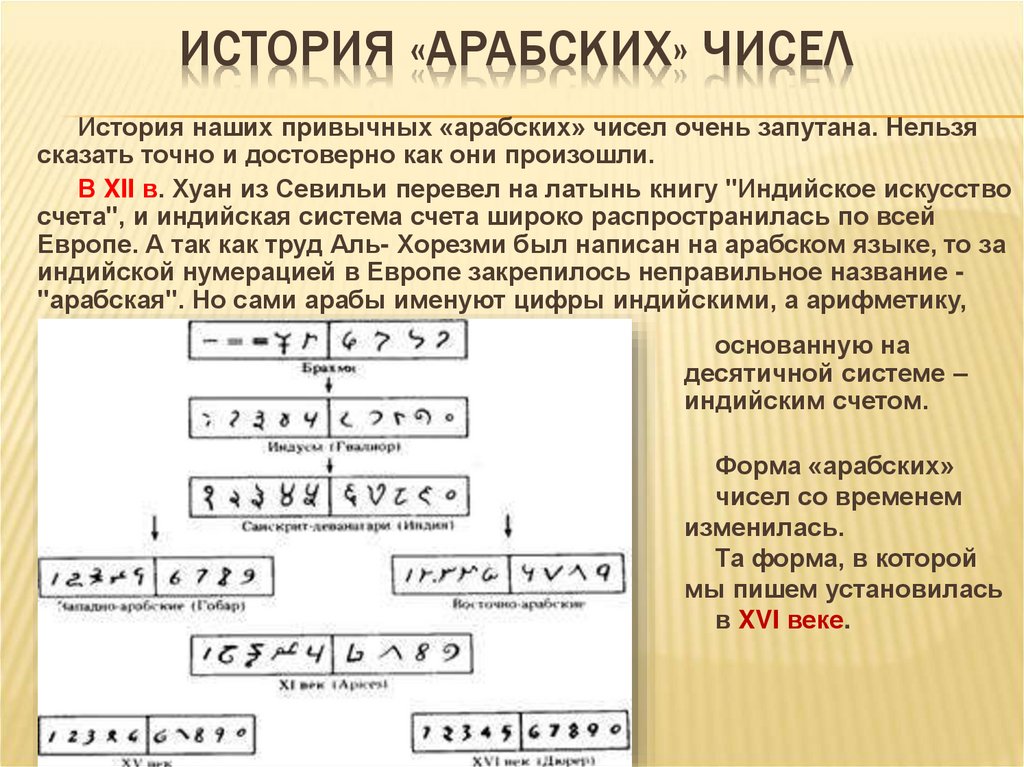
32. История «арабских» чисел

ИСТОРИЯ «АРАБСКИХ» ЧИСЕЛ
История наших привычных «арабских» чисел очень запутана. Нельзя
сказать точно и достоверно как они произошли.
В XII в. Хуан из Севильи перевел на латынь книгу "Индийское искусство
счета", и индийская система счета широко распространилась по всей
Европе. А так как труд Аль- Хорезми был написан на арабском языке, то за
индийской нумерацией в Европе закрепилось неправильное название "арабская". Но сами арабы именуют цифры индийскими, а арифметику,
основанную на
десятичной системе –
индийским счетом.
Форма «арабских»
чисел со временем
изменилась.
Та форма, в которой
мы пишем установилась
в XVI веке.

33. Такими были наши числа

ТАКИМИ БЫЛИ НАШИ ЧИСЛА

34.

Впервые нуль появился в древневавилонской системе
счисления, он использовался для обозначения пропущенных
разрядов в числах . Изобретателем формы нуля можно
считать великого греческого астронома Птолемея. Но
Птолемей использует нуль в том же смысле, что и
вавилоняне.
Леонардо Фибоначчи, в своем сочинении "Liber abaci"
(1202) называет знак 0 по-арабски zephirum. Слово
zephirum – это арабское слово as-sifr, которое произошло от
индийского слова sunya, т. е. пустое, служившего названием
нуля. От слова zephirum произошло французское слово zero
(нуль) и итальянское слово zero. С другой стороны, от
арабского слова as-sifr произошло русское слово цифра.
Вплоть до середины XVII века это слово употреблялось
специально для обозначения нуля. Латинское слово nullus
(никакой) вошло в обиход для обозначения нуля в XVI веке.

35. Из истории

ИЗ ИСТОРИИ
Двоичной системой счисления пользовался в
начале 17 в. Т.Харриот. Позднее Г.Лейбниц
обратил на двоичную систему внимание
миссионеров, отправлявшихся для проповеди
христианства в Китай в надежде убедить
китайского императора в том, что Бог (единица)
сотворил все из ничего (нуля). Однако вплоть до
20 в. двоичную систему рассматривали как
своего рода математический курьез, и время от
времени раздавались предложения перейти от
десятичной системы к восьмеричной или
двенадцатеричной, но отнюдь не к двоичной
системе.