Logika

1.

Алгебра логики
При создании использовались материалы К. Полякова
http://kpolyakov.narod.ru/

2.

Что это?
Алгебра логики – раздел математики, изучающий
операции с логическими выражениями.
Логическое выражение (высказывание, условие) –
выражение, значением которого может быть либо
«истина», либо «ложь».
• Слон больше бегемота
• Москва – столица России
• a>b+c
• 2>5 ??

3.

И при чём здесь ПК?
В компьютерной технике операции с битами на
физическом уровне по сути подчиняются законам
алгебры логики.

4.

Сложное условие
Сложное условие –
несколько
простых
условий, объединенных
логическими
связками
(И, Или, Не).
Если (я буду учить)
ИЛИ (мне повезет)
«Коль себя не пожалеешь,
То опять помолодеешь»

5.

НЕ (инверсия)
Для анализа возможных результатов сложных условий
строят таблицы истинности (ТИ).
ТИ – это таблица, где в левой части записываются все
возможные сочетания исходных данных, а в правой –
значение сложного условия целиком.
Инверсия изменяет значение логического выражения
на противоположное.
А
не А
0
1
1
0

6.

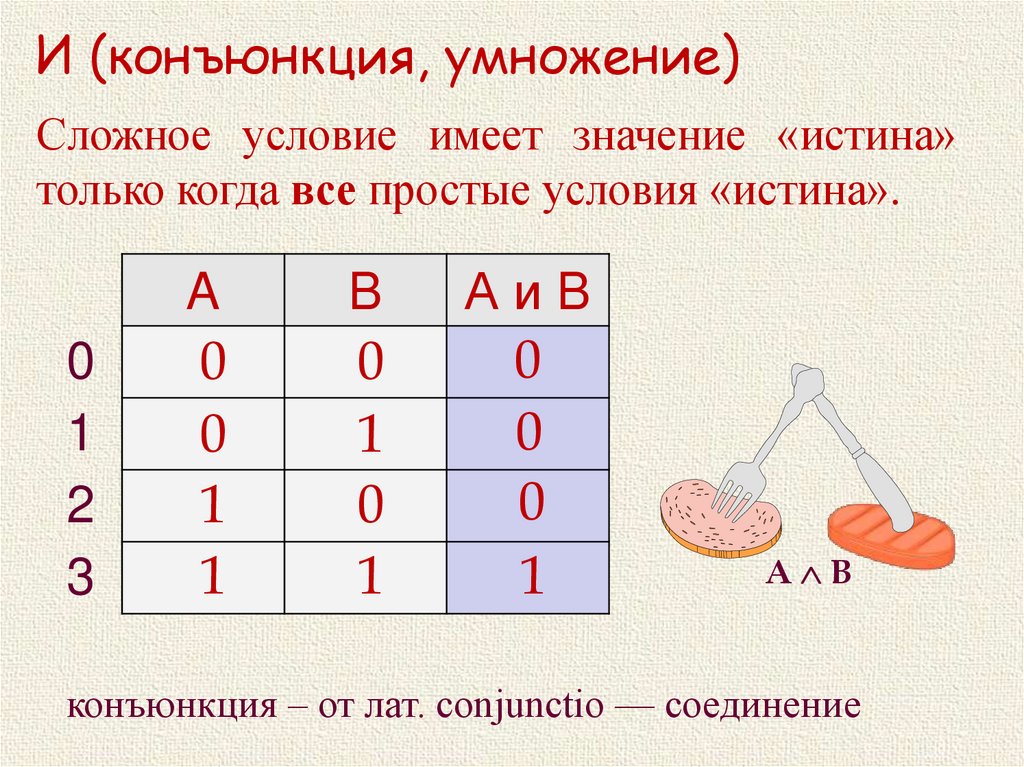
И (конъюнкция, умножение)
Сложное условие имеет значение «истина»
только когда все простые условия «истина».
0
1
2
3
A
B
АиB
0
0
1
1
0
1
0
1
0
0
0
1
A B
конъюнкция – от лат. conjunctio — соединение

7.

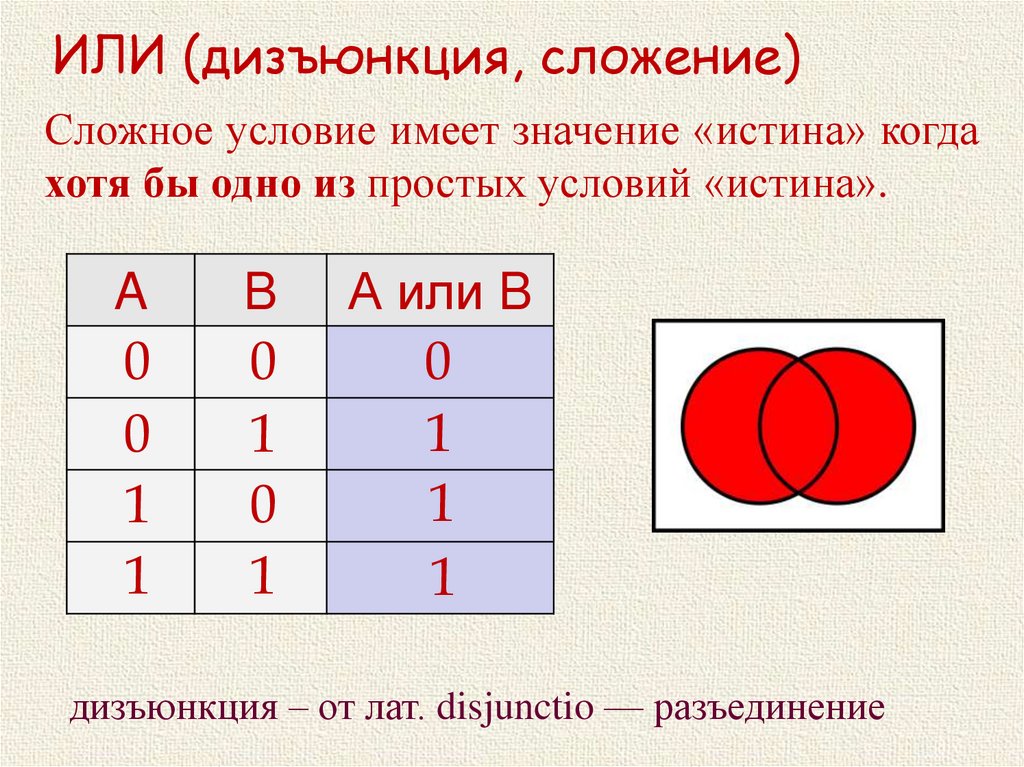
ИЛИ (дизъюнкция, сложение)
Сложное условие имеет значение «истина» когда
хотя бы одно из простых условий «истина».
A
B
А или B
0
0
1
1
0
1
0
1
0
1
1
1
дизъюнкция – от лат. disjunctio — разъединение

8.

Импликация («если …, то …»)
Сложное условие имеет значение «истина»
когда из «истины» не следует «ложь».
A – «Работник хорошо работает».
B – «У работника хорошая зарплата».
A
0
0
1
1
B
0
1
0
1
А B
1
1
0
1

9.

Эквивалентность (тогда и только тогда)
Сложное условие имеет значение «истина»
когда оба высказывания одинаковы.
A
0
0
1
1
B
0
1
0
1
А B
1
0
0
1

10.

Законы алгебры логики
Название
для И
для ИЛИ
A A
двойного отрицания
A A 0
A A 1
операции с
константами
A 0 0, A 1 A
A 0 A, A 1 1
повторения
A A A
A A A
поглощения
A ( A B) A
A A B A
переместительный
A B B A
A B B A
исключения третьего
сочетательный
A (B C) ( A B) C A (B C) ( A B) C
распределительный
A B C ( A B) ( A C) A (B C) A B A C
законы де Моргана
A B A B
A B A B
10

11.

Круги Эйлера

12.

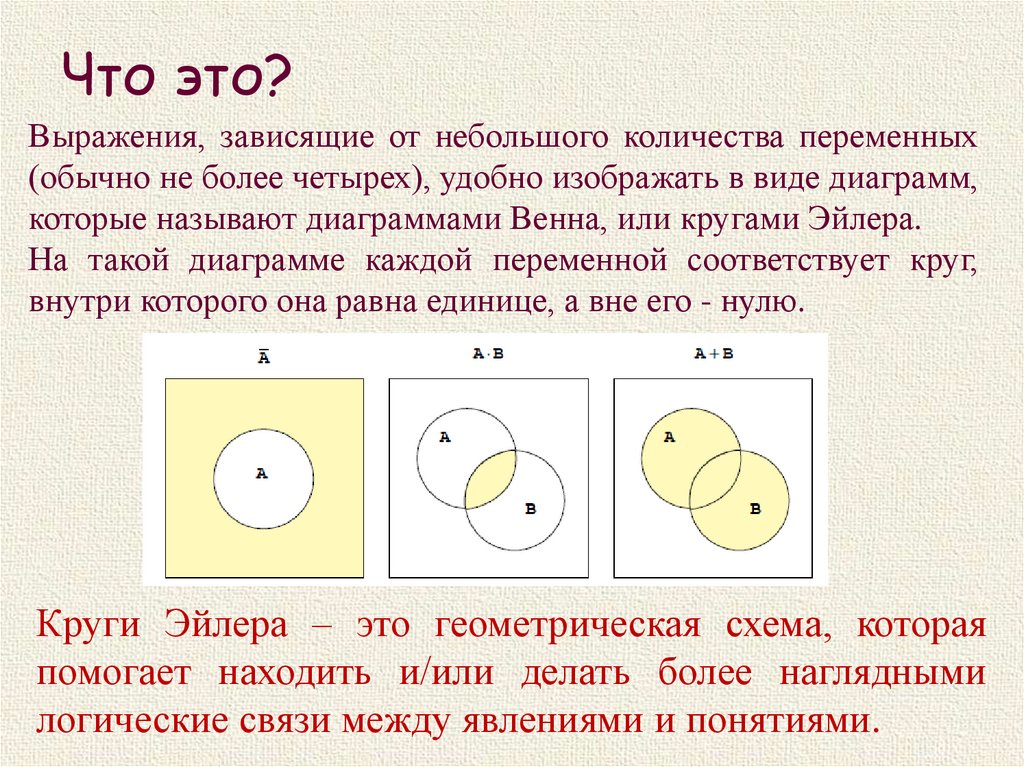
Что это?
Выражения, зависящие от небольшого количества переменных
(обычно не более четырех), удобно изображать в виде диаграмм,
которые называют диаграммами Венна, или кругами Эйлера.
На такой диаграмме каждой переменной соответствует круг,
внутри которого она равна единице, а вне его - нулю.
Круги Эйлера – это геометрическая схема, которая
помогает находить и/или делать более наглядными
логические связи между явлениями и понятиями.

13.

Где используют?
Диаграммы удобно применять для решения задач, в
которых используются множества, например, множества
ссылок, полученных от поисковой системы в ответ на
какой-то запрос.
Орки (В)
Хоббиты (А)
1
2
3
А = 1+2
В = 2+3
AиВ=2
А или В = 1+2+3

14.

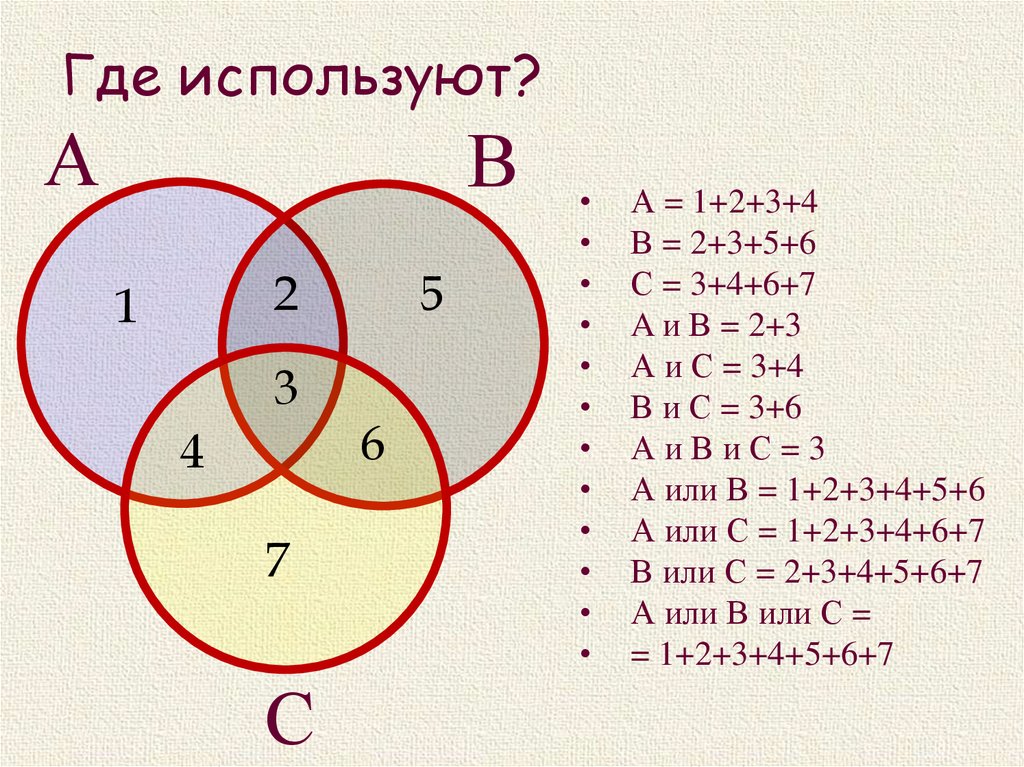
Где используют?
А
В
2
1
3
4
7
С
5
6
А = 1+2+3+4
В = 2+3+5+6
С = 3+4+6+7
A и В = 2+3
А и С = 3+4
В и С = 3+6
АиВиС=3
А или В = 1+2+3+4+5+6
А или С = 1+2+3+4+6+7
В или С = 2+3+4+5+6+7
А или В или С =
= 1+2+3+4+5+6+7

15.

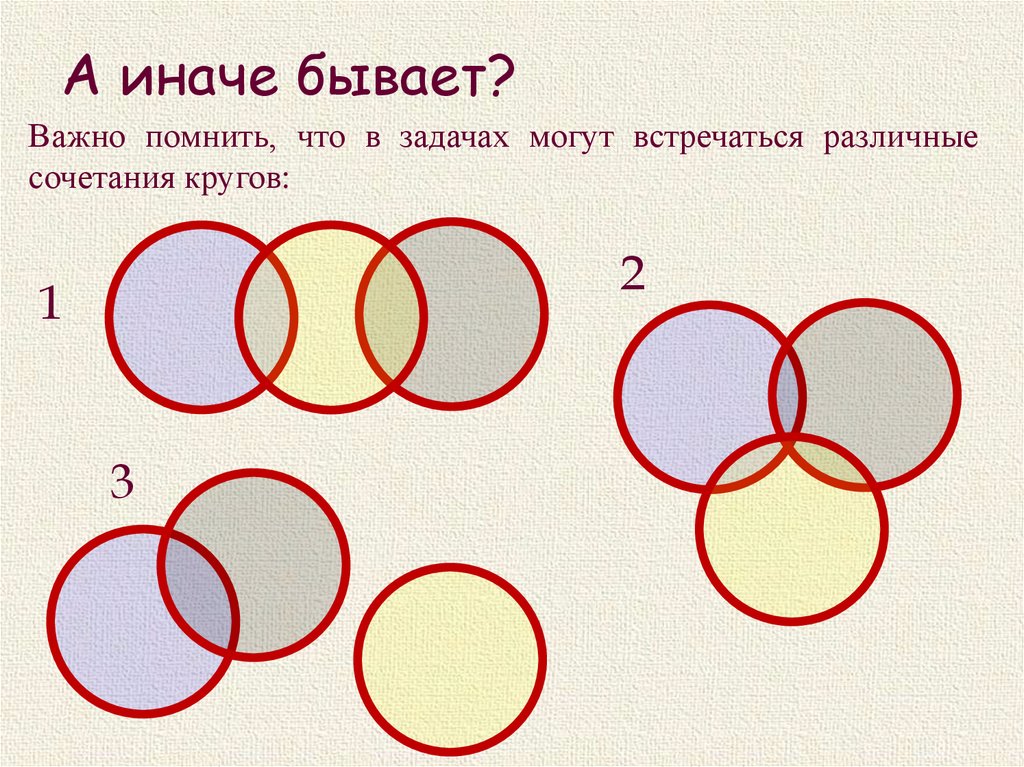
А иначе бывает?
Важно помнить, что в задачах могут встречаться различные
сочетания кругов:
2
1
3