Пределы и непрерывность

1.

Пределы и непрерывность.
Кафедра «Математика и моделирование»
СГТУ имени Гагарина Ю.А.

2.

Определение предела по Коши
Пусть функция y f x определена в некоторой окрестности точки x0
R, т. е. x0 – некоторое конечное число.
Рассмотрим поведение функции по мере приближения x к точке x0.
Определение (по Коши). Постоянное число А называется пределом
функции f(x) в точке x0 (или при x x0), если для произвольного числа >0
найдется число ( ) >0 такое, что из условия 0< x - x0 < вытекает
неравенство f(x) - A < .
Обозначение:
lim f ( x) A.
x x0
С помощью кванторов
следующем виде:
def
данное
определение
можно
записать
lim f ( x) A 0 ( ) 0 : x : 0 x x0 f ( x) A
x x0
в

3.

Определение предела по Коши
def
lim f ( x) A 0 ( ) 0 : x : 0 x x0 f ( x) A
x x0
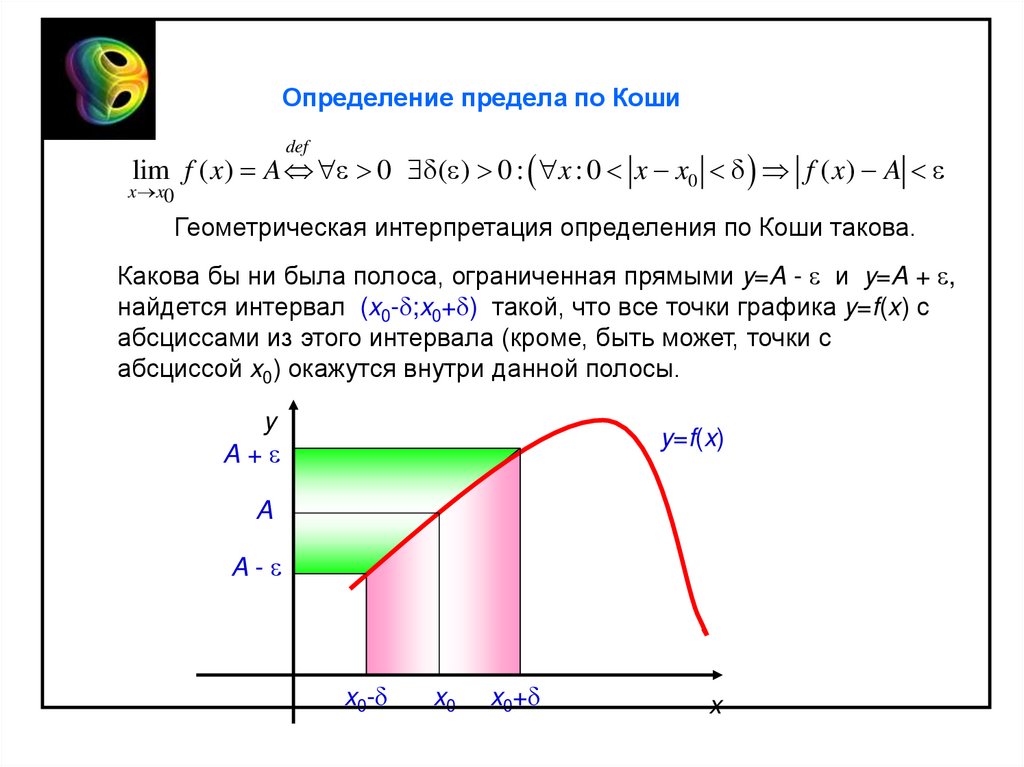
Геометрическая интерпретация определения по Коши такова.
Какова бы ни была полоса, ограниченная прямыми y=A - и y=A + ,
найдется интервал (x0- ;x0+ ) такой, что все точки графика y=f(x) с
абсциссами из этого интервала (кроме, быть может, точки с
абсциссой x0) окажутся внутри данной полосы.
y
A+
y=f(x)
A
A-
x0-
x0
x0+
x

4.

Определение предела по Коши
o
U ( x0 )
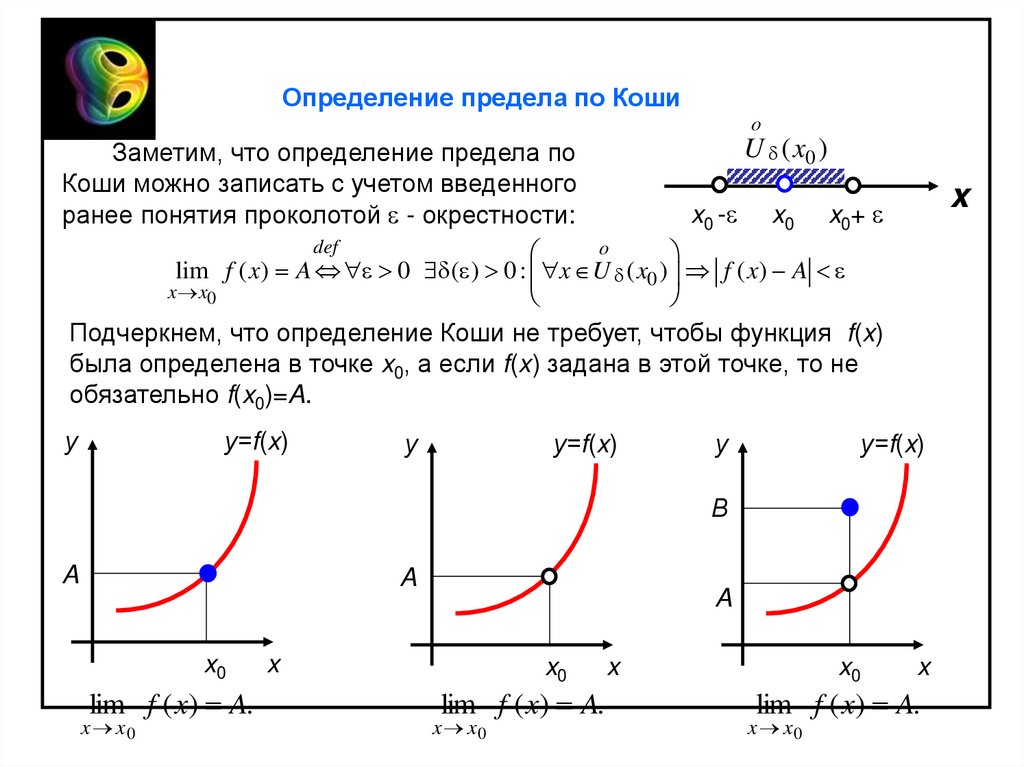
Заметим, что определение предела по
Коши можно записать с учетом введенного
x0 - x0 x0+
ранее понятия проколотой - окрестности:
def
o
lim f ( x) A 0 ( ) 0 : x U ( x0 ) f ( x) A
x x0
Подчеркнем, что определение Коши не требует, чтобы функция f(x)
была определена в точке x0, а если f(x) задана в этой точке, то не
обязательно f(x0)=A.
у
у=f(x)
у
у=f(x)
у
x
x
у=f(x)
В
A
A
x0
lim f ( x) A.
x x0
A
x
x0
lim f ( x) A.
x x0
x
x0
x
lim f ( x) A.
x x0

5.

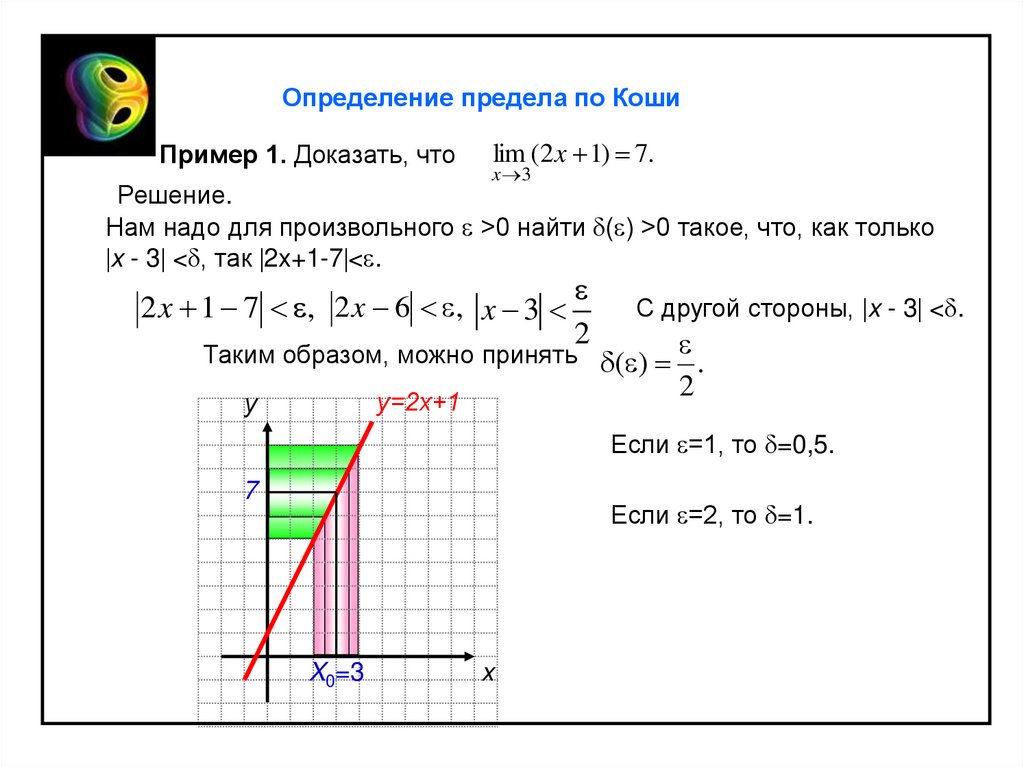
Определение предела по Коши
Пример 1. Доказать, что
lim (2 x 1) 7.
x 3
Решение.
Нам надо для произвольного >0 найти ( ) >0 такое, что, как только
x - 3 < , так 2x+1-7 < .
2 x 1 7 , 2 x 6 , x 3
2
С другой стороны, x - 3 < .
Таким образом, можно принять ( ) .
2
у=2х+1
у
Если =1, то =0,5.
7
Если =2, то =1.
X0=3
x

6.

Определение предела по Коши
2
Пример 2. Доказать, что lim x 4.
x 2
Решение.
Нам надо для произвольного >0 найти ( ) >0 такое, что, как только x –
2 < , так х2 - 4 < или
( x 2)( x 2) .
Но x – 2 < , и при условии <1 имеем:
x 2 ( x 2) 4 x 2 4 4 5.
Таким образом,
x 2 4 ( õ 2)( õ 2) 5 .
С другой стороны х2 - 4 < .
.
Таким образом, можно принять
5

7.

Определение предела по Коши
Пример 4. Доказать, что
lim e x 0.
x
Решение.
Необходимо доказать существование числа M >0 такого, что e-x <
при x>M.
| e x |
1
x ln
Следовательно, в качестве искомого числа M можно взять
1
M ln .

8.

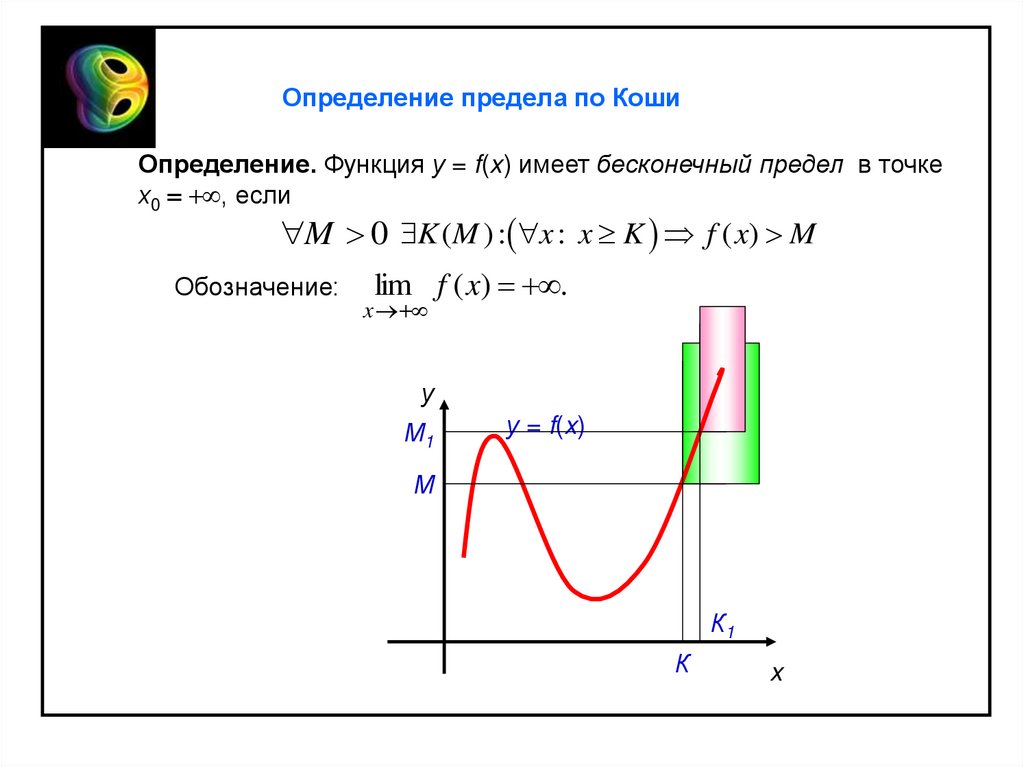
Определение предела по Коши
Определение. Функция у = f(x) имеет бесконечный предел в точке
х0 , если
M 0 K (M ) : x : x K f ( x) M
Обозначение:
lim f ( x) .
x
у
М1
у = f(x)
М
К1
К
x

9.

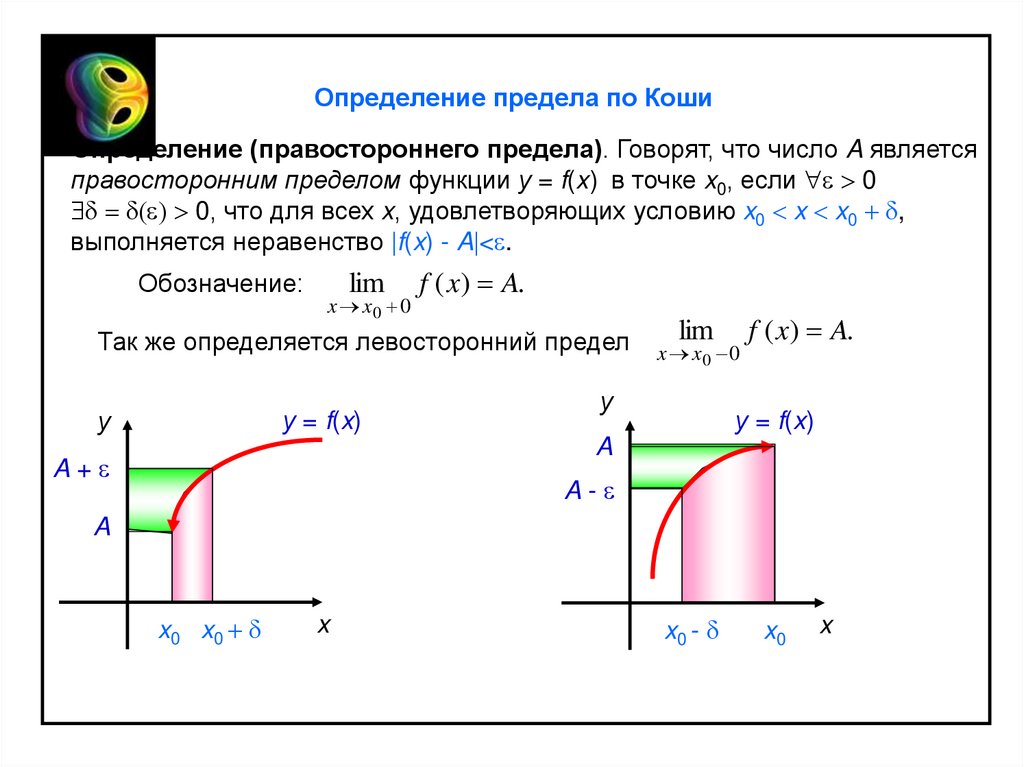
Определение предела по Коши
Определение (правостороннего предела). Говорят, что число A является
правосторонним пределом функции у = f(x) в точке x0, если 0
0, что для всех x, удовлетворяющих условию x0 x x0 ,
выполняется неравенство f(x) - A < .
Обозначение:
lim
x x0 0
f ( x) A.
Так же определяется левосторонний предел
у = f(x)
у
lim
x x0 0
у
f ( x) A.
у = f(x)
A
A+
A-
A
x0 x0
x
x0 -
x0
x

10.

Определение предела по Коши
Пример 6. Найти односторонние пределы функции
при x 0 и х .
4 e
Решение.
При х +0 (т. е. справа) 1 ,
x
e
1
,
x
e
При х –0 (т. е. слева)
При х
1
0,
x
3
f ( x) 2
e
1
x
1,
1
x
1
x
0,
,
lim f ( x) 2
x 0
1
x
3 11
.
4 4
lim f ( x) 2 0 2.
x 0
lim f ( x) 2
x
3 13
.
5 5

11.

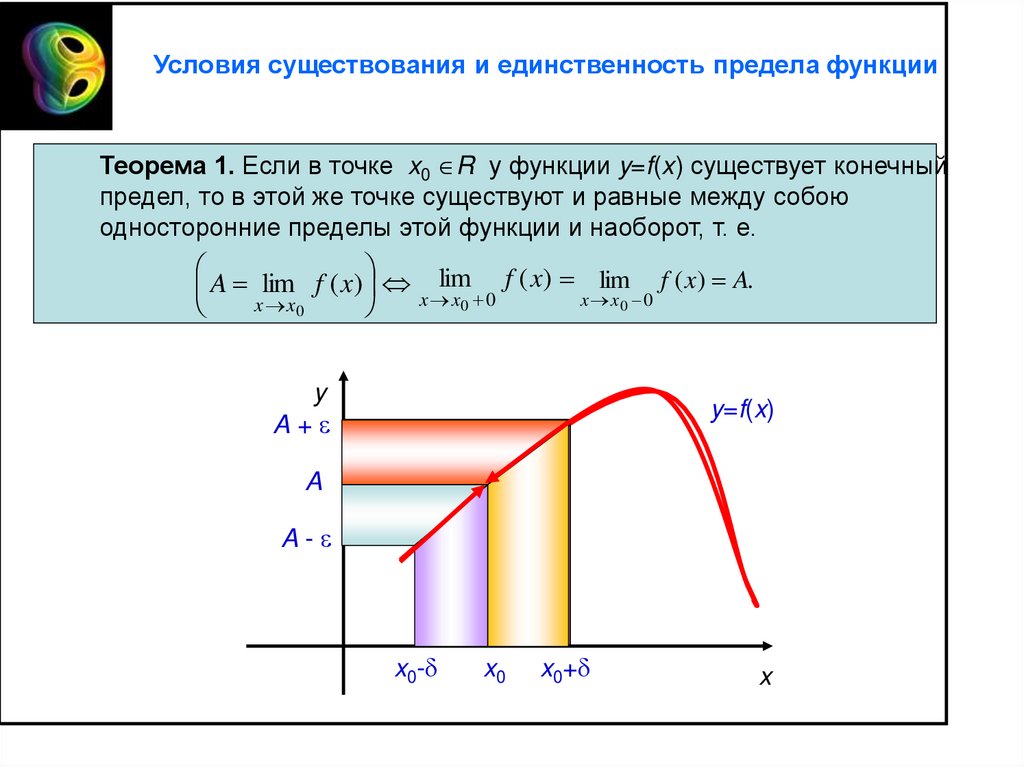
Условия существования и единственность предела функции
Теорема 1. Если в точке x0 R у функции y=f(x) существует конечный
предел, то в этой же точке существуют и равные между собою
односторонние пределы этой функции и наоборот, т. е.
f ( x) lim f ( x) A.
A lim f ( x) x lim
x x0 0
x
0
0
x x0
y
A+
y=f(x)
A
A-
x0-
x0
x0+
x

12.

Условия существования и единственность предела функции
Теорема 2 (о единственности предела). Если в точке x0 R данная
функция y=f(x) имеет конечный предел, то он единственный.
Доказательство.
Допустим, что в данной точке x0 R существуют два различных предела:
lim f ( x) A1 0:
x x0
lim f ( x) A2 0:
x x0
o
0
x
U
x
:
f
x
A
1
1 1
1 0
2
o
2 2 0 x U 2 x0 : f x A2 2
Очевидно, что оба утверждения тем более будут иметь место, если
заменить в них 1 и 2 на min 1, 2 , а тогда оказывается, что
o
0: 0 x U x0 :
A1 A2 A1 f x f x A2 f x A1 f x A2
A1 A2
С другой стороны, число выбирается произвольно, и мы можем взять
его удовлетворяющим неравенствам 0 A1 A2 . Полученное
противоречие и доказывает теорему.

13.

Условия существования и единственность предела функции
Теорема 3 (достаточный признак существования предела). Если
lim g ( x) lim h( x) A,
x x0
x x0
и в некоторой окрестности точки x0 (кроме, быть может, самой точки x0)
выполняется условие
g ( x) f ( x) h( x),
то функция y=f(x) имеет в точке x0 предел, и этот предел равен А.
куда они меня
тащут?

14.

Арифметические операции над пределами
Теорема 1. Если существуют
lim f ( x) A, lim g ( x) В,
x x0
x x0
то существует и
lim ( f ( x) g ( x)) A B.
x x0
Доказательство.
Докажем теорему для случая, когда x0 R, т.е. является конечным
вещественным числом.
o
0 ( 1 1( ) 0)( x U 1 ( x0 )) : A f ( x) A ;
2
2
o
0 ( 2 2 ( ) 0)( x U 2 ( x0 )) : B g ( x) B .
2
2
Возьмем δ = min {δ1, δ2}, тогда оба утверждения останутся в силе, и
сложив почленно неравенства, имеющие одинаковый знак, получим:
o
0 ( ( ) 0)( x U ( x0 )) : A B f ( x) g ( x) A B ;
а это и означает, что
lim f ( x) g ( x) lim f ( x) lim g ( x).
x x0
x x0
x x0

15.

Арифметические операции над пределами
lim f ( x) A, lim g ( x) В,
Теорема 2. Если существуют
x x0
x x0
то существует и
lim ( f ( x) g ( x)) A B.
x x0
Теорема 3. Если существуют
lim f ( x) A, lim g ( x) В 0, то существует и
x x0
x x0
lim f ( x)
f ( x) x x 0
A
.
x x 0 g ( x)
lim g ( x) B
lim
x x0
Приведенные теоремы о пределах позволяют решать вопросы о
нахождении пределов сложных (составных) функций.

16.

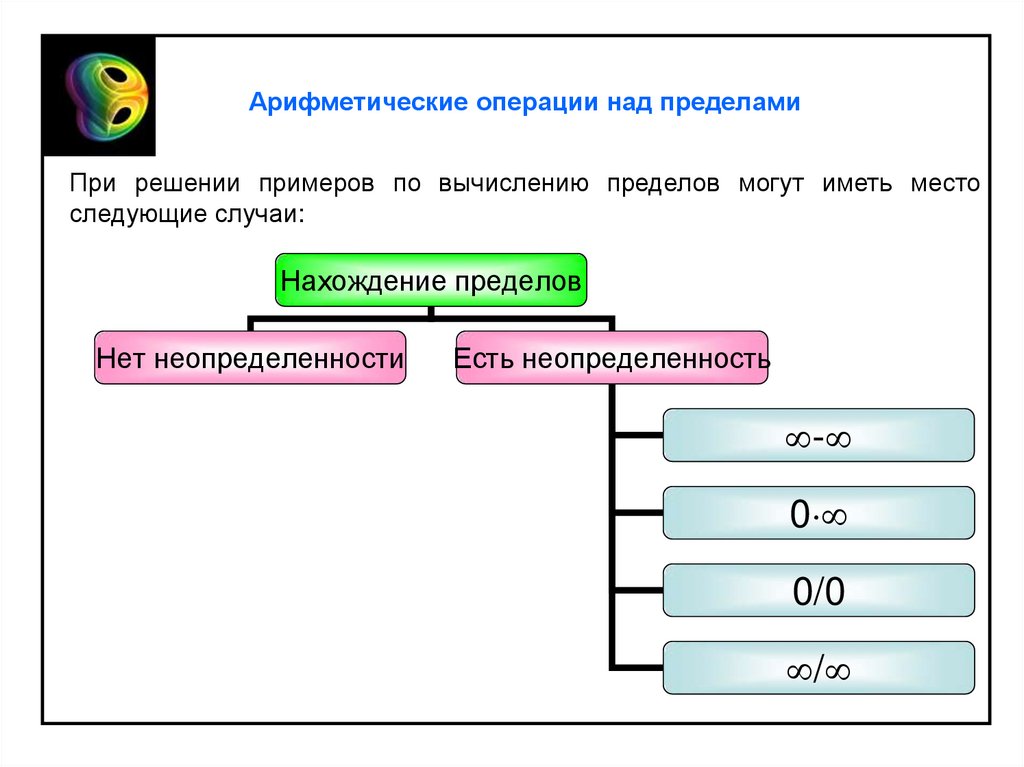
Арифметические операции над пределами
При решении примеров по вычислению пределов могут иметь место
следующие случаи:
Нахождение пределов
Нет неопределенности
Есть неопределенность
-
0
0/0
/

17.

Арифметические операции над пределами
П 1.2.1. Случай отсутствия неопределенности
В простейших случаях отсутствия неопределенности нахождение
предела функции сводится к подстановке предельного значения
аргумента в функцию: если f(x)
– элементарная функция,
определенная в точке x0, то
lim f ( x) f ( lim x) f ( x0 ).
x x0
x x0
Отметим при этом, что:
C
0.
x x 0 f ( x)
C
(C 0).
2) если f(x) при x x0, то lim
x x 0 f ( x)
1) если f(x) 0 при x x0, то lim
g ( x)
0.
x x 0 f ( x)
3) если g(x) 0 и f(x) при x x0, то lim

18.

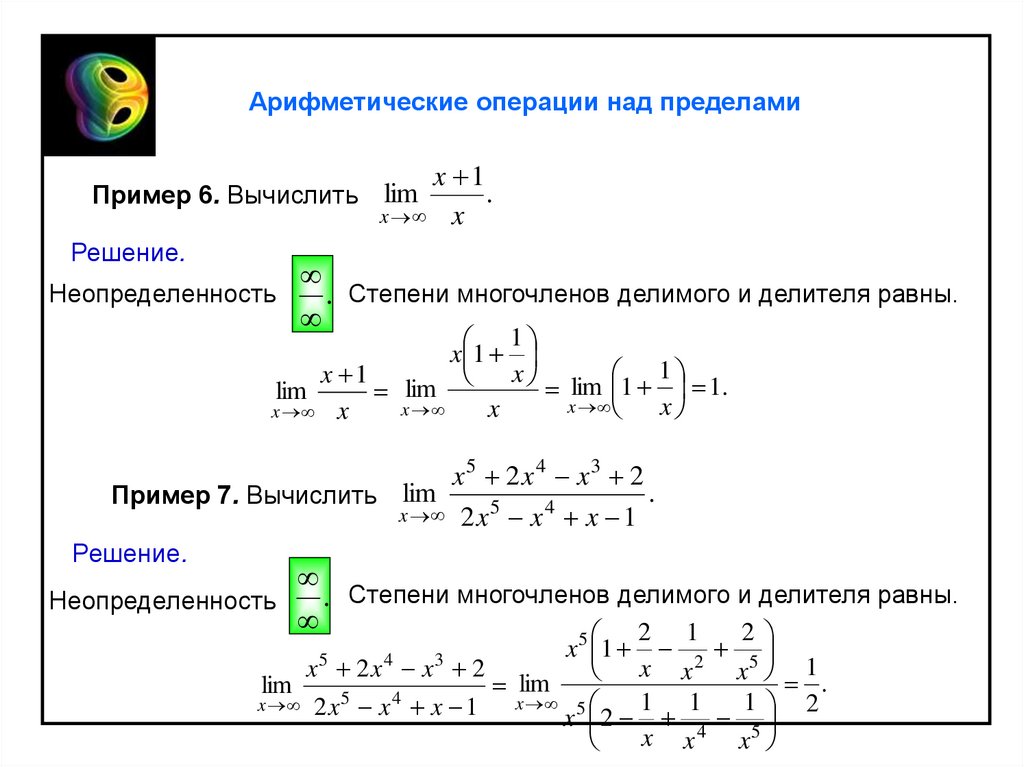
Арифметические операции над пределами
Пример 1. Вычислить
x
.
x 2 x 1
lim
Решение.
Заметим, что в точке x = 2 данное выражение принимает значение,
равное 2. При x = 2 здесь нет неопределенности, таким образом
x
lim
2.
x 2 x 1
Пример 2. Вычислить
x
.
x 1 x 1
lim
Решение.
При x = 1 здесь нет неопределенности.
Очевидно, что
x
1
lim
.
x 1 x 1 0

19.

Арифметические операции над пределами
0
П 1.2.2. Раскрытие неопределенности .
0
Рекомендуем придерживаться следующих правил:
1. Если под знаком предела стоят дробно-рациональные функции, то в
этом случае в числителе и знаменателе выделяется множитель x - x0 и
рассматривается выражение, получаемое после сокращения на этот
множитель.
2). В примерах, содержащих иррациональности, полезно применять
следующие формулы:
ax 2 bx c a x x1 x x2
a 3 b3 a b a 2 ab b 2
a b a b
a b 3 a 3 b 3 a 2 3 ab 3 b 2
a b

20.

Арифметические операции над пределами
x3 1
.
Пример 3. Вычислить lim 2
x 1 x 1
Решение.
Очевидно, что мы имеем неопределенность
0
.
0
Эту неопределенность вносят множители (х-1) в числителе и знаменателе.
Для раскрытия неопределенности необходимо выделить эти множители.
x2 x 1 3
( x 1)( x 2 x 1)
.
lim
lim 2
lim
x 1
2
x 1
x 1
( x 1)( x 1)
x 1 x 1
x3 1

21.

Арифметические операции над пределами
x6 1
Пример 4. Вычислить lim
x 1 x 3 2 x 2 x 2
.
Решение.
Очевидно, что мы имеем неопределенность
0
.
0
Эту неопределенность вносят множители (х-1) в числителе и знаменателе.
Для раскрытия неопределенности необходимо выделить эти множители.
lim
x6 1
x 1 x 3 2 x 2 x 2
lim
x 1
lim
( x 1)( x 2 x 1)( x 3 1)
x 1
x ( x 2) ( x 2)
2
( x 1)( x 2 x 1)( x 3 1)
( x 2 1)( x 2)
( x 1)( x 2 x 1)( x 3 1)
lim
x 1
( x 1)( x 1)( x 2)
( x 2 x 1)( x 3 1) 3 2
lim
1.
x 1
( x 1)( x 2)
6

22.

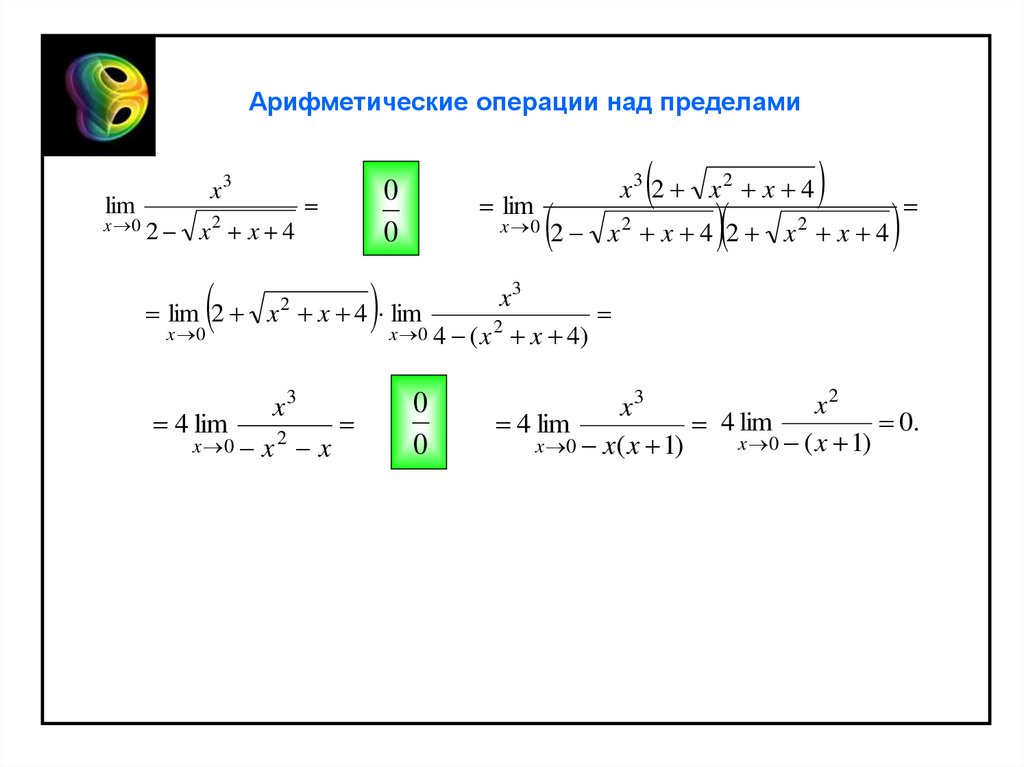
Арифметические операции над пределами
Пример 5. Вычислить lim
Решение.
x 0 2
x3
x x 4
2
.
Очевидно, что мы имеем неопределенность
0
.
0
Данный предел содержит иррациональность в знаменателе.
Решение состоит из следующих шагов:
– избавиться от иррациональности (домножить на сопряженное);
– в полученном рациональном выражении разложить числитель и
знаменатель на простые множители;
– избавиться от неопределенности и вычислить предел.

23.

Арифметические операции над пределами
lim
x3
x 0 2
x x 4
2
0
0
lim
x 0 2
x3 2 x 2 x 4
x x 4 2 x x 4
2
2
x3
lim 2 x x 4 lim
x 0
x 0 4 ( x 2 x 4)
4 lim
2
x3
x 0 x 2 x
0
0
x2
x3
0.
4 lim
4 lim
x 0 ( x 1)
x 0 x( x 1)

24.

Арифметические операции над пределами
П 1.2.3. Раскрытие неопределенности .
Рекомендуем пользоваться следующим правилом:
Если надо найти предел отношения двух многочленов при х , то
сравнивают их высшие степени.
Возможны три случая:
1.Степени многочленов числителя и знаменателя равны. Тогда предел
отношения будет равен рациональной дроби, у которой в числителе и
знаменателе будут стоять коэффициенты при высших степенях
многочленов.
2.Степень многочлена знаменателя больше числителя. Тогда предел
отношения будет равен нулю.
3. Степень многочлена знаменателя меньше числителя. Тогда предел
отношения будет равен бесконечности.

25.

Арифметические операции над пределами
Пример 6. Вычислить
Решение.
Неопределенность
x 1
.
x x
lim
. Степени многочленов делимого и делителя равны.
1
x 1
x lim 1 1 1.
x 1
lim
lim
x
x
x
x
x x
x5 2 x 4 x3 2
.
Пример 7. Вычислить lim
x 2 x5 x 4 x 1
Решение.
. Степени многочленов делимого и делителя равны.
Неопределенность
2 1
2
5
x 1 2 5
x x
x 1.
lim
lim
x 5
1 1
1 2
x 2x5 x 4 x 1
x 2 4 5
x x
x
x5 2x 4 x3 2

26.

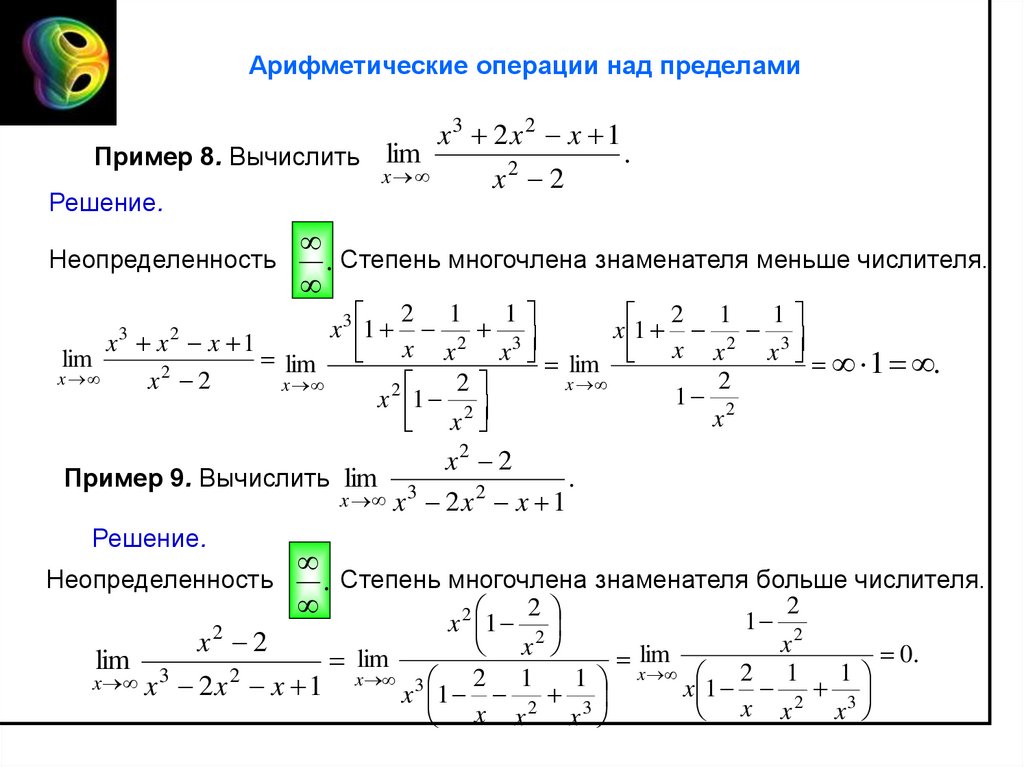
Арифметические операции над пределами
x3 2 x 2 x 1
.
Пример 8. Вычислить lim
2
x
x 2
Решение.
Неопределенность
. Степень многочлена знаменателя меньше числителя.
1
1
2 1
2 1
x 3 1 2 3
x 1 2 3
x x x 1
x lim x x
x
x x
lim
lim
1 .
2
x
2
x 2
x
x
2
1 2
x 2 1 2
x
x
3
2
x2 2
.
Пример 9. Вычислить lim 3
x x 2 x 2 x 1
Решение.
Неопределенность
. Степень многочлена знаменателя больше числителя.
2
2
2
1
x 1 2
2
x 2
x
x
0.
lim
lim 3
lim
x
2
1
1
2
x 3
2 1
1
x x 2 x x 1
x 1 2 3
x 1 2 3
x
x x
x
x x
2

27.

Арифметические операции над пределами
П 1.2.4. Раскрытие неопределенности
Пример 10. Вычислить
Решение.
x 2 x 1 .
x
lim
Неопределенность
.
x 2 x 1
x
lim
lim
lim
x
x
x 2x 1
1 x
lim
x 2 x 1 x x 2 x 1
1
1
x 1
x 1
x
x .
lim
1
1 x
1
2
x 1 2
x
x

28.

Пределы ограниченных функций
Теорема 1 (ограниченность функции, имеющей конечный
предел). Если в точке x0 R функция f (x) имеет конечный предел, то
в некоторой проколотой окрестности точки x0 функция f (x)
ограничена.

29.

Пределы ограниченных функций
Теорема 1 (ограниченность функции, имеющей конечный
предел). Если в точке x0 R функция f (x) имеет конечный предел, то
в некоторой проколотой окрестности точки x0 функция f (x)
ограничена.
Теорема 2. Если в окрестности точки x0 имеет место неравенство (х)
≤ (х) и существуют конечные пределы
lim ( x) A, lim ( x) B,
то A ≤ B.
x x0
x x0
Теорема 3. Если функция у = f(x) монотонна и ограничена в проколотой
окрестности точки x0 R, то тогда существуют конечные левосторонний и
правосторонний пределы функции у = f(x) в точке x0.
Теорема 4. Если функция у = f(x)
не убывает (не возрастает)
на бесконечном промежутке X и ограничена сверху (снизу), то она
имеет конечный предел при х .

30.

Коши впервые дал четкое определение
основным понятиям математического
анализа – пределу, непрерывности
функции, сходимости ряда и т.д.
Коши Огюстен Луи
1789 — 1857,
французский математик,
член Парижской АН (1816).
О продуктивности Коши-математика
свидетельствует целый ряд терминов,
определений и понятий, вошедших в науку,
таких, как признак Коши, критерий Коши,
задачи Коши, интеграл Коши, уравнения
Коши–Римана и Коши–Ковалевской,
относящиеся к разным разделам
математического анализа, математической
физики, теории чисел, и других дисциплин.
Всего же он написал 700 работ (по другим
источникам 800), с неимоверной легкостью
переходя от одной области научного знания
к другой.
Коши - Абель
Коши - Галуа

31.

Замечательные пределы
Первый замечательный предел
Пусть х – величина угла, лежащего в первой четверти, в радианах.
Сравним площади трех фигур:
1
1
1
1
1
1
Scek. R 2 x x. S ОВС R 2 tg x tg x.
S OAC R 2 sin x sin x.
2
2
2
2
2
2
1
1
1
В
sin x x tg x
А
2
2
2
О
2
x
1
0
:
1
.
Умножаем неравенство на
х
sin x
sin x cos x
sin x
С
1 x 0 ; .
Отсюда cos x
x
2
Рассуждая аналогично, получим это же неравенство
o
Но ;0 0; U (0) есть проколотая окрестность точки 0.
2 2
x ; 0 .
2
lim cos x 1, lim 1 1 в силу достаточного признака существования предела
x 0
x 0
sin x
1.
x 0 x
lim

32.

Замечательные пределы
Первый замечательный предел
Cледствия из первого замечательного предела:
sin kx k lim sin kx
1). lim
k 1 k.
kx
0
kx
x 0
x
tg kx
sin kx
1
2). lim
k lim
k 1 k.
x 0 x
kx 0 kx
cos kx
sin kx lim sin kx x k 1 k .
3). lim
m m
x 0 sin mx x 0 x sin mx
tg kx x
tg kx
1 k
k .
lim
m m
x 0 tg mx x 0 x tg mx
arcsin x
y
5). lim
lim
1, где y = arcsin x.
x 0
y
0
x
sin y
4). lim
arctg x
y
lim
1,
x 0
y 0 tg y
x
6). lim
где y = arctg x.
2
x
sin
2 sin
2
1
1 cos x
2
2
2 1 .
2
lim
lim
7). lim
x 0 x
x 0
x 0
2
x2
2
x2
2 x

33.

Замечательные пределы
Понятие последовательности и ее предела
Определение. Если каждому натуральному n по какому-либо известному
правилу поставлено в соответствие некоторое число an, тогда говорят, что
задана числовая последовательность, которая обозначается как {an}.
Правило, по которому формируется последовательность {an}, обозначается
как an=f(n) и называется общим членом последовательности.
Примеры числовых последовательностей:
а) 1, –1, 1, –1, ...
аn ( 1)n 1, n N ;
б) 0, 1, 0, –1, 0,... аn sin(
с) 1,
1 1
1
, ,..., n ,...
2 4
2
d) 1, 4, 9, 16, 25,...
an
n
) sin (n 1),
2 2
2
1
2
n
n N;
аn n 2 , n N .
n N;

34.

Замечательные пределы
Понятие последовательности и ее предела
Числовую последовательность {an} можно считать функцией дискретного
аргумента n и применить к ней определение предела функции по Коши:
Число А называется пределом числовой последовательности {an} ,
если >0 N( ) >0 такое, что при n > N an-A < .
При этом пишут lim an A.
n

35.

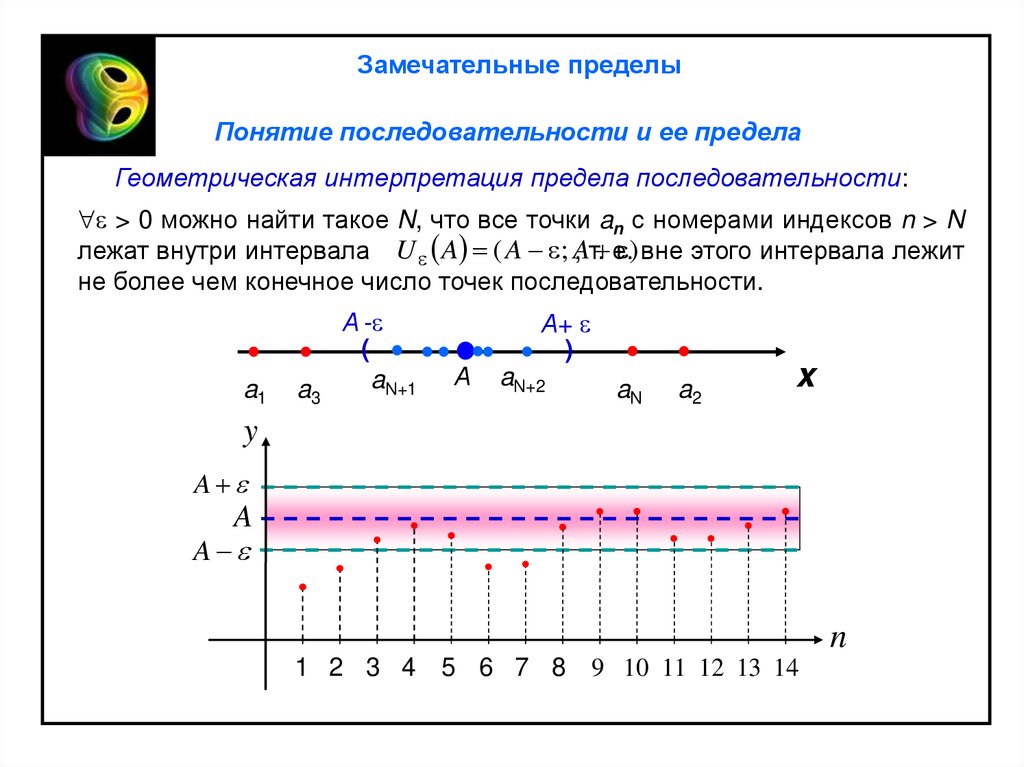
Замечательные пределы
Понятие последовательности и ее предела
Геометрическая интерпретация предела последовательности:
> 0 можно найти такое N, что все точки an с номерами индексов n > N
) вне этого интервала лежит
лежат внутри интервала U A ( A ; A
, т. е.
не более чем конечное число точек последовательности.
a1
a3
А -
(
aN+1
А
А+
)
aN+2
xaN
a2
x
y
A
A
A
n
1 2 3 4
5 6 7 8
9 10 11 12 13 14

36.

Замечательные пределы
Понятие последовательности и ее предела
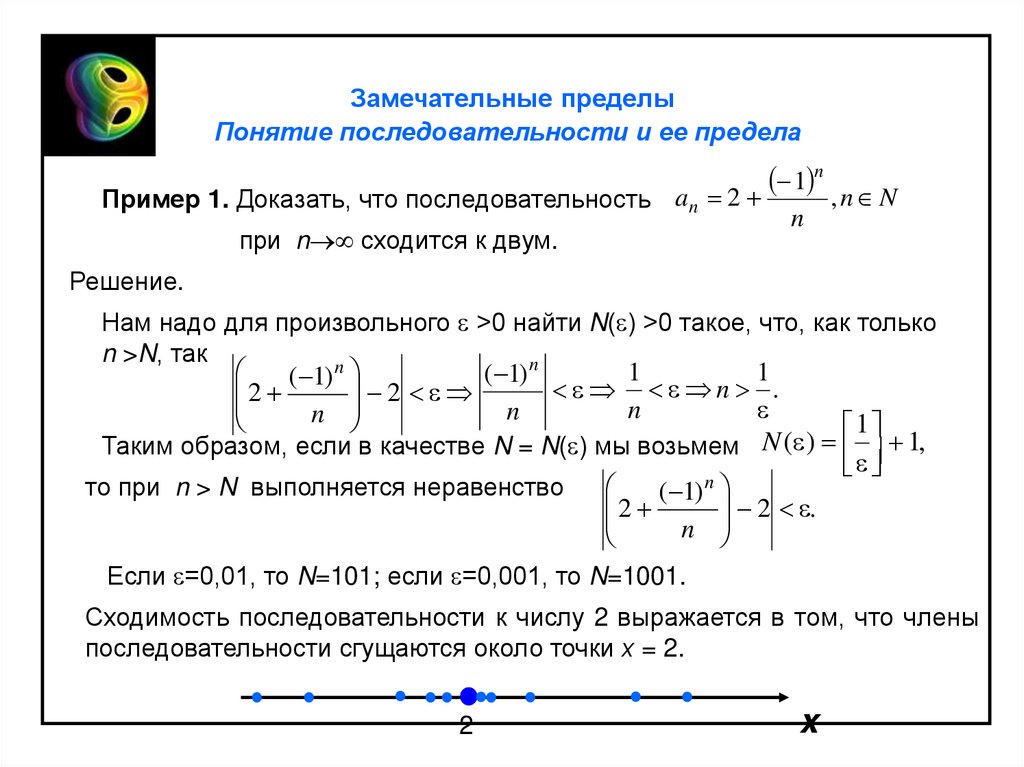
Пример 1. Доказать, что последовательность
1 n
a 2
,n N
n
n
при n сходится к двум.
Решение.
Нам надо для произвольного >0 найти N( ) >0 такое, что, как только
n >N, так
n
1
1
( 1) n
(
1
)
n
.
2
2
n
n
n
1
Таким образом, если в качестве N = N( ) мы возьмем N ( ) 1,
2 ( 1) 2 .
n
Если =0,01, то N=101; если =0,001, то N=1001.
то при n > N выполняется неравенство
n
Сходимость последовательности к числу 2 выражается в том, что члены
последовательности сгущаются около точки х = 2.
2
x

37.

Замечательные пределы
Понятие последовательности и ее предела
Поскольку последовательность является частным случаем функции, то
достаточно очевидно, что для предела последовательности имеют место
основные теоремы, справедливые для предела функции:
1. Последовательность может иметь только один предел.
2. Если последовательность {an} имеет предел, то она ограничена.
3. Если последовательность {an}
возрастает (или не убывает) и
ограничена сверху, то она имеет предел.
Очевидно, что правила нахождения пределов последовательностей
аналогичны правилам, установленным для пределов функции.

38.

Замечательные пределы
Понятие последовательности и ее предела
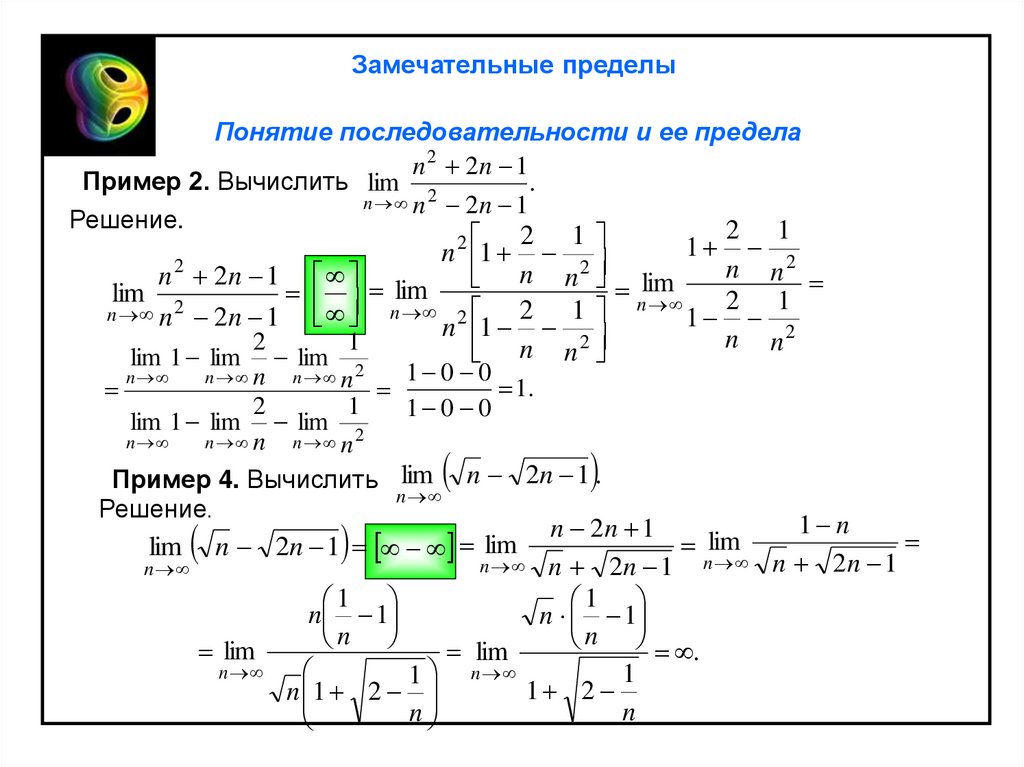
n 2 2n 1
Пример 2. Вычислить lim 2
.
n n 2n 1
Решение.
2 1
2 1
2
1 2
n
1
2
2
n n
n n lim
n 2n 1
n
lim 2
lim
2
1
n n 2n 1
n n 2 1 2 1
1 2
n n
n n 2
2
1
lim 1 lim lim
n
n n
n n 2
2
1
lim 2
n n n n
lim 1 lim
n
1 0 0
1.
1 0 0
Пример 4. Вычислить lim n 2n 1 .
n
Решение.
1 n
n 2n 1
lim
lim n 2n 1 lim
n
n 2n 1
n n 2n 1
n
1
1
n 1
n 1
n
n .
lim
lim
n
1
1 n
1 2
n 1 2
n
n

39.

Замечательные пределы
Второй замечательный предел для последовательностей
Можно доказать две леммы.
n
1
Лемма 1. Последовательность a n 1 возрастает с ростом n.
n
n
1
Лемма 2. Последовательность a n 1 ограничена.
n
Следовательно, справедлива теорема:
Теорема.
1
a n 1
n
Последовательность
n
, где n =1;2;3…. ,
стремится к конечному пределу, заключенному между 2 и 3.
Этот предел определяет число Непера
1
e lim 1
n
n
n
e 2,718281828

40.

Замечательные пределы
Второй замечательный предел для последовательностей
"Секретные изобретения" Непера -1596 г:
Джон Не́пер
1550—1617
шотландский математик, один
из изобретателей логарифмов
• зеркало для сжигания вражеских
кораблей на любом заданном расстоянии;
• устройство для плавания под водой с
ныряльщиками, различными
приспособлениями и военными
хитростями для нанесения вреда врагу;
• круглую колесницу, непробиваемую
выстрелами из сдвоенного мушкета и
движимую теми, кто находится внутри;
• орудие, при выстреле из которого ядра
летят не по прямой линии, поражая, как у
других, лишь то, что случайно окажется
на его пути, но движется, рыская, над
поверхностью целого заданного района и
не покидает его до тех пор, пока не
израсходует свою силу.

41.

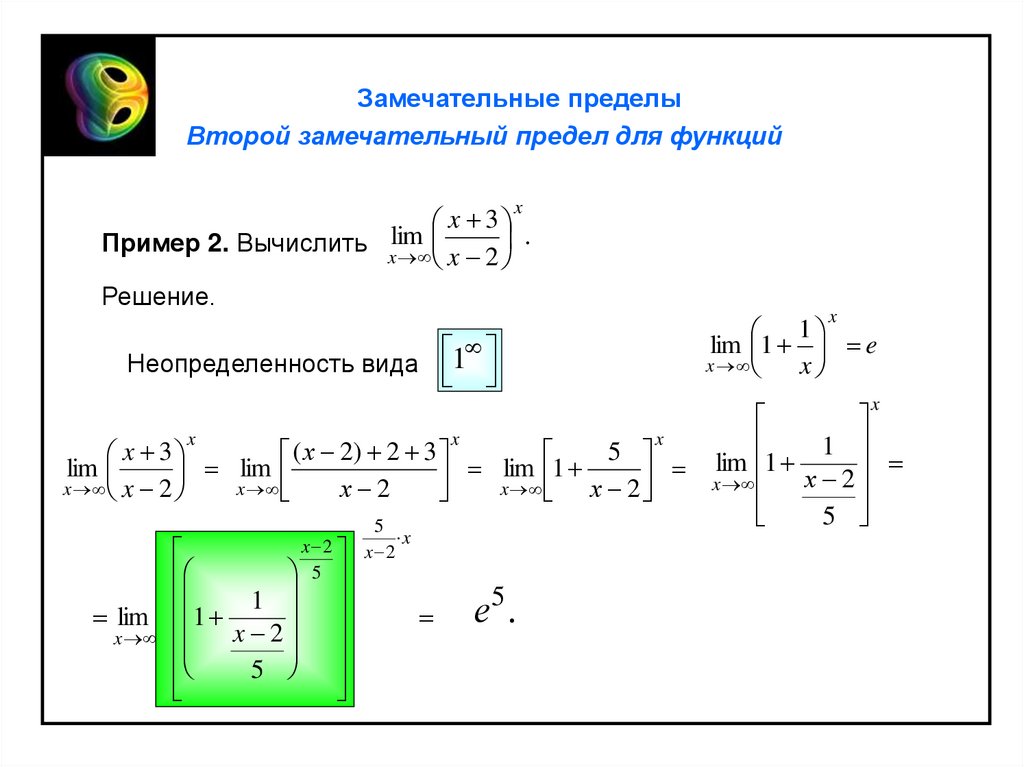
Замечательные пределы
Второй замечательный предел для функций
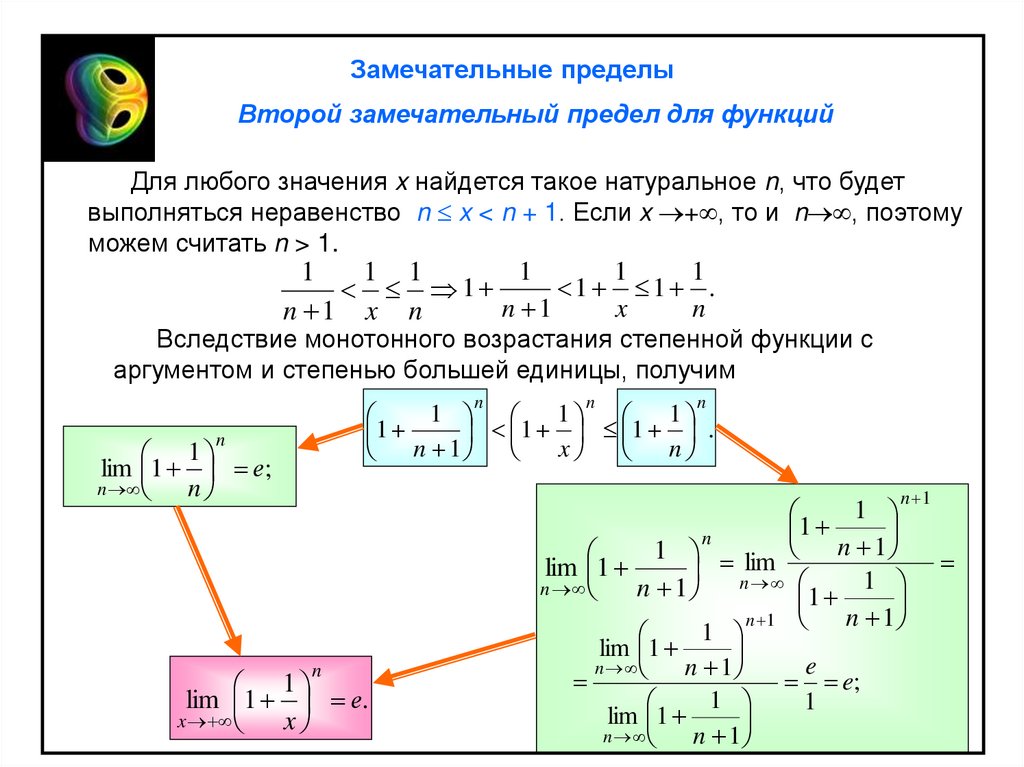
Для любого значения x найдется такое натуральное n, что будет
выполняться неравенство n x < n + 1. Если x + , то и n , поэтому
можем считать n > 1.
1
1
1
1
1 1
1 1 .
1
n 1
x
n
n 1 x n
Вследствие монотонного возрастания степенной функции с
аргументом и степенью большей единицы, получим
n
n
n
1 1 1
1
1 1 .
n 1
x
n
n
1
lim 1 е;
n
n
n 1
n
1
lim 1 е.
x
x
1
1
n
n
1
1 lim
lim 1
n
1
n
n 1
1
n 1
n 1
1
lim 1
n
e
n 1
e;
1
1
lim 1
n
n 1

42.

Замечательные пределы
Второй замечательный предел для функций
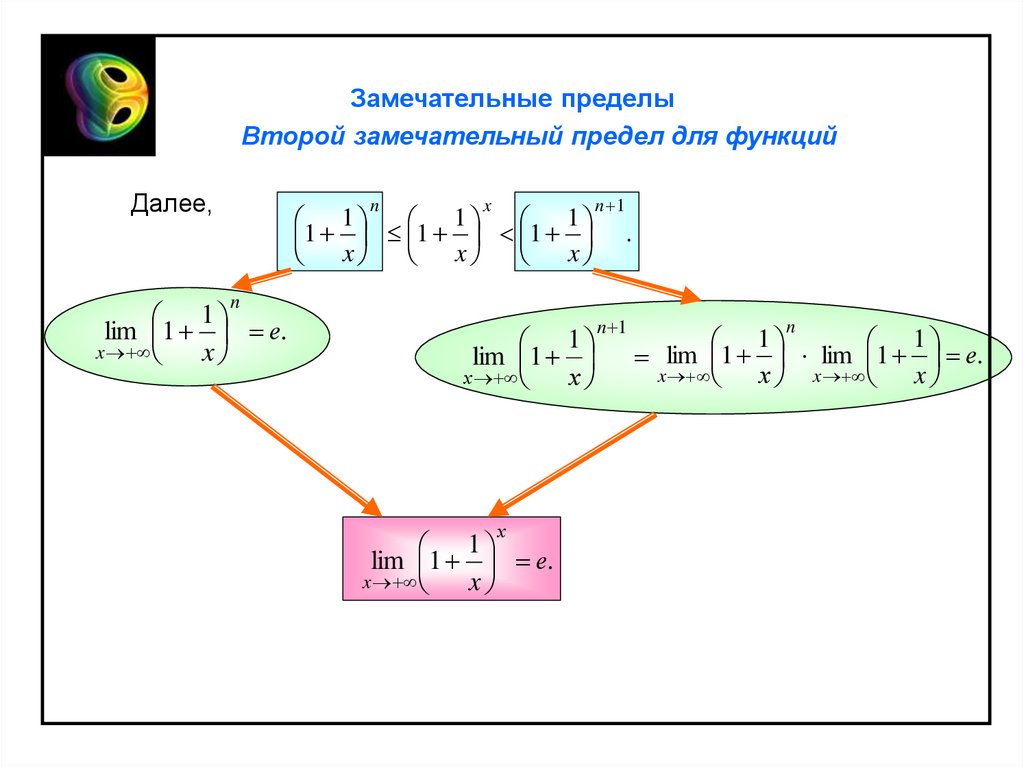
Далее,
n
x
1 1 1
1 1 1
x
x
x
n 1
.
n
1
lim 1 е.
x
x
1
lim 1
х
х
х
1
lim 1 е.
x
x
n 1
n
1
1
lim 1 lim 1 е.
x
х x x

43.

Замечательные пределы
Второй замечательный предел для функций
Пусть теперь x – .
Введем новую переменную y= -x -1, тогда y + при x – .
x
1
1
lim 1 lim 1
x
x
y
y 1
1
lim 1
y
y
y 1
y 1
1
lim 1
y
y
y
y
lim
y y 1
y 1
y 1
lim
y y
y 1
1
1
lim 1 e 1 e.
y
y
Мы доказали, что односторонние пределы при x существуют и равны,
поэтому
x
1
lim 1 e
- второй замечательный предел.
x
x
Это предельное соотношение можно записать в другом виде
1
1
x n
n
x
1
x
lim 1 x e
x 0

44.

Замечательные пределы
Второй замечательный предел для функций
Следствия из второго замечательного предела:
1
1
1
ln(1 x)
1). lim
lim ln(1 x) lim ln(1 x) x ln( lim (1 x) x ) ln e 1.
x 0
x 0 x
x 0
x 0
x
y
y
a x 1 lim
ln
a
lim
ln a.
2). lim
y
0
log
(
1
y
)
y
0
ln(1 y)
x 0
x
a
ex 1
3). lim
ln e 1.
x 0
x

45.

Замечательные пределы
Второй замечательный предел для функций
1
Пример 1. Вычислить lim (1 7 x) x .
x 0
1
Решение. lim 1 x e
x
x 0
Неопределенность вида 1
1
1
( 7 )
x
7
x
lim (1 7 x) lim (1 ( 7 x))
xlim
0
x 0
x 0
1
7
1 7 x 7 x
е .

46.

Замечательные пределы
Второй замечательный предел для функций
x
x 3
lim
.
Пример 2. Вычислить x
x
2
Решение.
Неопределенность вида 1
x
1
lim 1 e
x
x
x
x
x
x
1
5
x 3
( х 2) 2 3
lim
1
lim
lim 1
lim
х
2
x
x x 2
x
x
х 2
х 2
5
5
x
x 2 x 2
5
5
1
е
.
lim 1
x
2
x
5

47.

Замечательные пределы
Второй замечательный предел для функций
Пример 3. Вычислить
lim x ln( x 3) ln( x 2) .
x
Решение.
x
5
x 3
lim
ln
1
lim x ln( x 3) ln( x 2) lim ln
x
x
x
x
2
x
2
5
ln lim 1
x
x 2
x 5
5
x 2 x 2 x
5
ln lim 1 5
x
x 2
x 5
ln е 5.
5
1

48.

Определение предела функции по Гейне
Дадим другое определение предела функции.
Определение (по Гейне). Постоянное число А называется пределом
функции f(x) в точке x0, если для любой последовательности {xn} такой,
что xn x0 и xn x0, соответствующая последовательность значений
функции {f(xn)} сходится к А.
Определение по Гейне используется в основном в доказательствах
теорем (для доказательства факта, что предел не существует), в то время
как определение предела по Коши используют для доказательства того,
что
lim f ( x) A.
x x0

49.

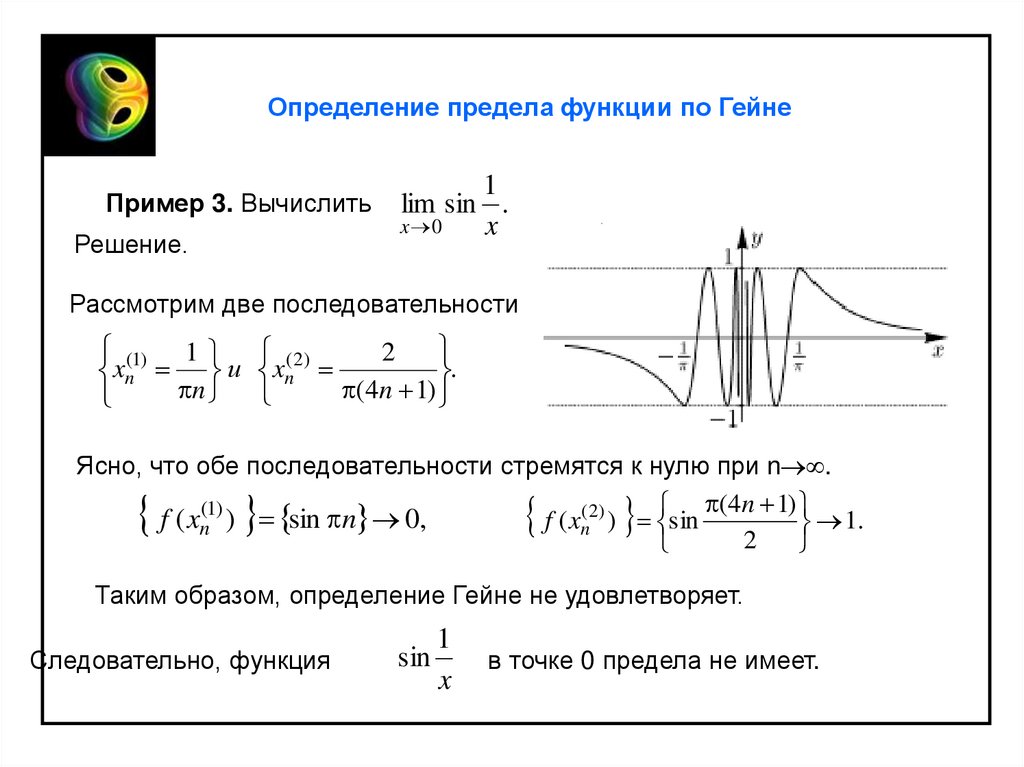
Определение предела функции по Гейне
Пример 3. Вычислить
Решение.
1
lim sin .
x 0
x
Рассмотрим две последовательности
(1) 1 ( 2)
2
x
и
x
n
n
.
n
(4n 1)
Ясно, что обе последовательности стремятся к нулю при n .
(4n 1)
f ( xn(1) ) sin n 0,
f ( xn( 2) ) sin
1.
2
Таким образом, определение Гейне не удовлетворяет.
Следовательно, функция
sin
1
x
в точке 0 предела не имеет.

50.

Бесконечно малые функции
Ге́нрих Эдуа́рд Ге́йне
1821—1881
немецкий математик

51.

Бесконечно малые функции
Определение. Функция (х) называется бесконечно малой в точке х0, если
lim ( x) 0.
x x0
Примеры:
1). функция y=sinx является бесконечно малой при x , т. к.
lim sin x 0.
x
2). функция y=x3+1 является бесконечно малой в точке х0= -1, т. к.
lim x 3 1 0.
x 1
x 2 , при x 0
3). y ( x)
100, при x 0
бесконечно мала в точке х0=0, т.к.
lim y( x) 0.
x 0

52.

Бесконечно малые функции
Теорема 1. Сумма конечного числа бесконечно малых функций при
x x0 есть бесконечно малая функция.
Доказательство.
Докажем для двух функций (х) и (х).
( x ) :
( x) :
0 1 ( ) x : 0 x x0 1 ( x) ,
2
0 2 ( ) x : 0 x x0 2 ( x) .
2
Тогда для
min 1, 2
0 ( ) 0 x : 0 x x0 ( x) ( x) ( x) ( x)
что и доказывает условие теоремы.
,
2 2

53.

Бесконечно малые функции
Теорема 2. Произведение бесконечно малой функции (х) при x x0 на
функцию f(x), ограниченную в некоторой -окрестности точки x0, является
бесконечно малой при x x0.
Следствие 1. Произведение бесконечно малой на конечное число есть
бесконечно малая.
Следствие 2. Произведение двух или нескольких бесконечно малых есть
бесконечно малая.
Следствие 3. Линейная комбинация бесконечно малых есть
бесконечно малая.

54.

Бесконечно малые функции
Теорема 3. Для того чтобы функция f(x) имела при x x0 предел A,
необходимо и достаточно, чтобы f(x) можно было представить в виде
суммы f(x) =A+ (х), где (х) – бесконечно малая при x x0.
Доказательство.
Необходимость.
По условию и определению предела функции
0 ( ) 0 x : 0 x x0 f ( x) A
Следовательно, f ( x) A ( x) , т. е. (х) – бесконечно малая при
x x0, и функцию можно представить в виде f ( x) A ( x).
Достаточность. f ( x) A ( x), где (х) – бесконечно малая при x x0.
0 ( ) 0 x : 0 x x0 ( x)
( x) f ( x) A A lim f ( x).
x x0
В дальнейшем при доказательстве различных теорем мы будем
переходить от рассмотрения предела функции lim f x A
x x0
к рассмотрению бесконечно малой функции α x f x A в точке x0.

55.

Сравнение бесконечно малых функций
Рассмотрим в окрестности х0 две бесконечно малые функции α(х) и
β(х), для которых lim ( x) lim ( x) 0.
x x0
( x )
x x0 ( x)
А lim
0 | A |
А=1
x x0
Терминология
бесконечно малые
одного порядка
эквивалентные
бесконечно малые
А=0
(х) - бесконечно малая
более высокого порядка
по сравнению с (х)
А =
(х) - бесконечно малая
более низшего порядка
по сравнению с (х)
Обозначение
( x) O ( x)
( x) ~ ( x)
( х) o ( x)
( х) o ( x)

56.

Сравнение бесконечно малых функций
Смысл определения можно наглядно (но не строго) проиллюстрировать
следующим образом.
Если (х) – бесконечно малая функция более высокого порядка, чем
(х), то при x, близких к x0, значения (х) много меньше, чем значения
функции (х).
Иными словами, (х) стремится к нулю быстрее, чем (х).

57.

Сравнение бесконечно малых функций
Пример 1. Сравнить
( x) 1 cos5 x,
( x) x 2 .
Решение.
2
5x
2 5x
2
sin
2sin
5
25
1 cos5 x 0
( x)
2
2 2 lim
2
0.
lim
lim
lim
2
2
0
x
x
0
x
0
2
2
x
0
x 0 ( x)
x
x
Поэтому α(х) и β(х) – бесконечно малые одного порядка.
Пример 2. Сравнить
( x) x, ( x) sin 2 x.
Решение.
( x)
x2 1
x
lim
lim
lim
2
2
x 0 ( x)
x 0 sin x x
x 0 sin x
Поэтому α(х) - бесконечно малая более низшего порядка по сравнению с β(х).

58.

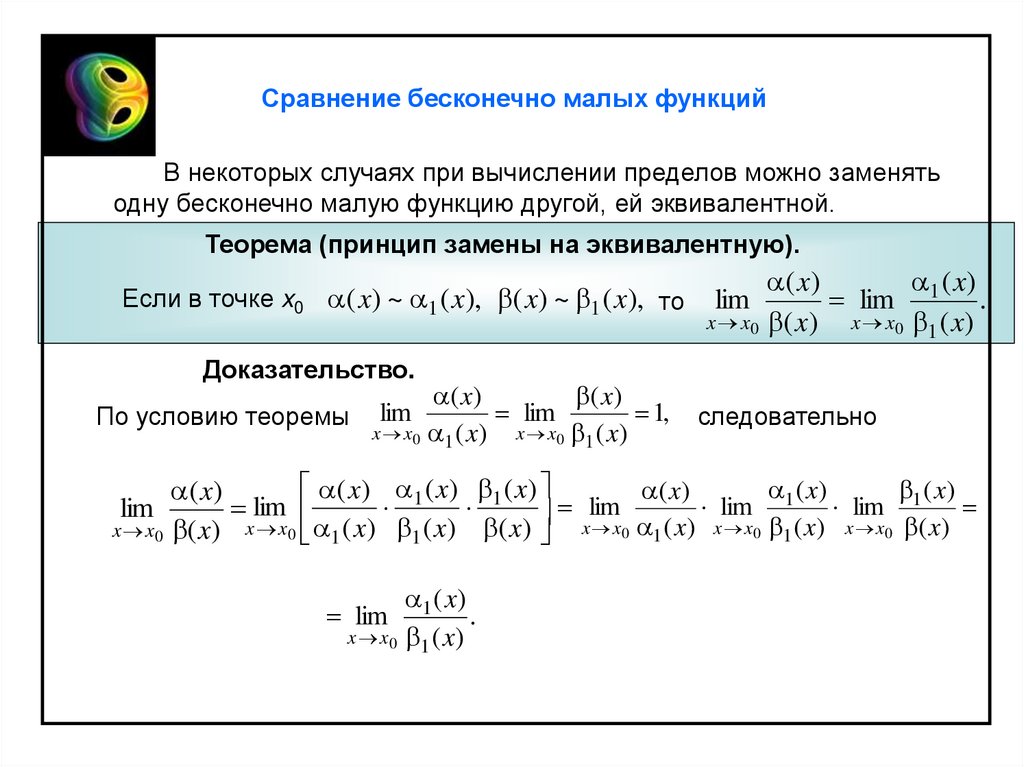
Сравнение бесконечно малых функций
В некоторых случаях при вычислении пределов можно заменять
одну бесконечно малую функцию другой, ей эквивалентной.
Теорема (принцип замены на эквивалентную).
Если в точке x0 ( x) ~ 1 ( x), ( x) ~ 1 ( x), то
( x)
( x)
lim 1 .
x x 0 ( x)
x x 0 1 ( x)
lim
Доказательство.
По условию теоремы
( x)
( x)
lim
1,
x x 0 1 ( x)
x x 0 1 ( x)
lim
следовательно
( x) 1 ( x) 1 ( x)
1 ( x)
1 ( x)
( x)
( x)
lim
lim
lim
lim
x
x
x
x
x
x
x
x
( x)
x x 0 ( x)
0 1 ( x)
0 1 ( x )
0 ( x )
0 1 ( x ) 1 ( x )
lim
1 ( x)
.
x x 0 1 ( x )
lim

59.

Сравнение бесконечно малых функций
Таблица эквивалентных бесконечно малых функций при х 0
sin x ~ x
a x 1 ~ x ln a
tg x ~ x
ex 1 ~ x
1 x 1 ~ x
n
1 x 1~
x
n
arcsin x ~ x
log a 1 x ~
x
ln a
1 x 1~
arctg x ~ x
ln 1 x ~ x
sh x ~ x
x2
1 cos x ~
2
x2
ch x 1 ~
2
x
2

60.

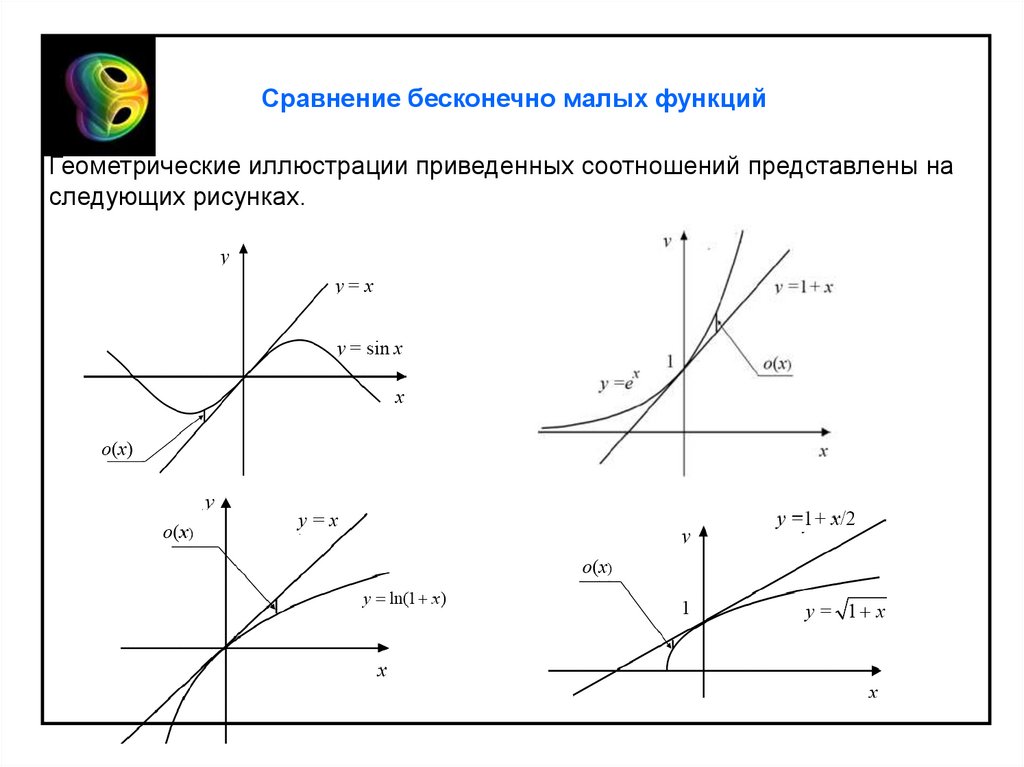
Сравнение бесконечно малых функций
Геометрические иллюстрации приведенных соотношений представлены на
следующих рисунках.

61.

Сравнение бесконечно малых функций
Примеры:
sin 7 x
7x 7
lim
1,4;
x 0 sin 5 x
x 0 5x
5
7x 7
sin 7 x
lim
3,5;
2) lim
x 0 2 x
2
x 0 tg 2 x
1) lim
2
ln(1 x x 2 ) lim x x lim 1 x 1 ;
3) lim
x 0 2 x
x 0 2
2
x 0
tg 2 x
3x
sin 3x
esin 3 x 1
lim
4) lim
lim
x 0 5 sin x
x 0 arctg(5 sin x)
x 0 ln(1 arctg(5 sin x))
3x
3
.
x 0 5 x
5
lim

62.

Бесконечно большие функции.
Шкала роста на бесконечности
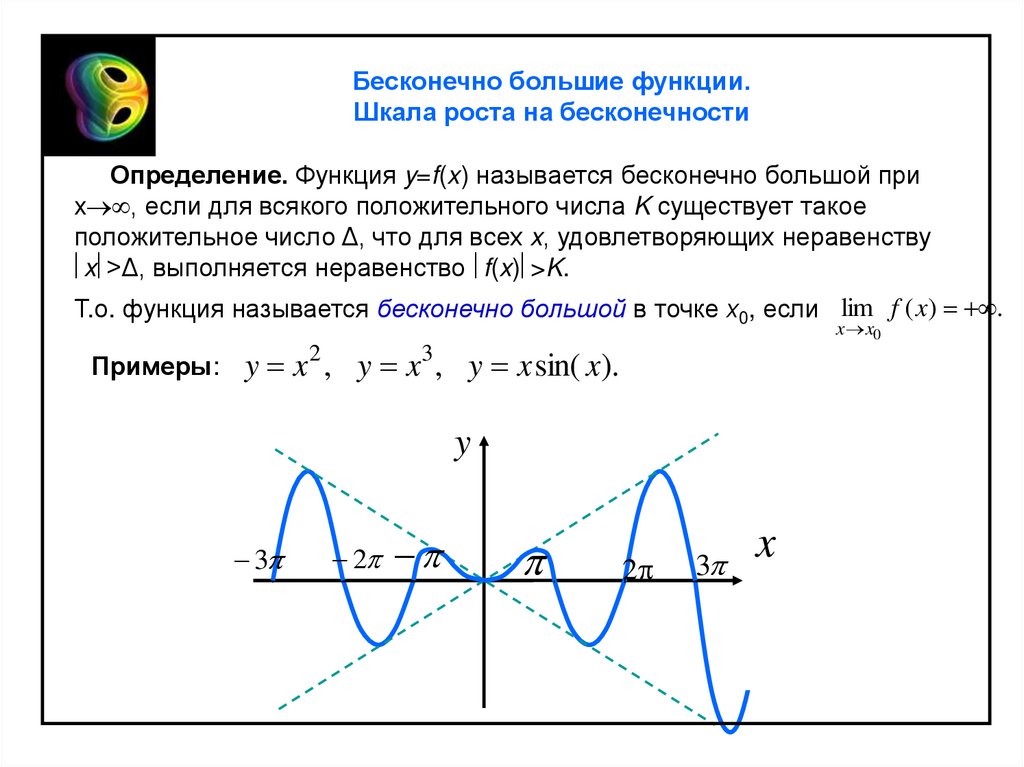
Определение. Функция y=f(x) называется бесконечно большой при
x , если для всякого положительного числа K существует такое
положительное число Δ, что для всех x, удовлетворяющих неравенству
x >Δ, выполняется неравенство f(x) >K.
Т.о. функция называется бесконечно большой в точке х0, если lim f ( x) .
Примеры:
x x0
y x 2 , y x3 , y x sin( x).
y
3
2
2
x
3

63.

Бесконечно большие функции.
Шкала роста на бесконечности
Для бесконечно больших можно ввести такую же систему классификации,
как и для бесконечно малых.
1. Бесконечно большие f(x) и g(x) считаются величинами одного
порядка, если
f ( x)
lim
A,| A | .
x x 0 g ( x)
2. Бесконечно большая f(x) считаются бесконечно большой более
высокого порядка по отношению к g(x), если
f ( x)
lim
x x 0 g ( x)
.

64.

Бесконечно большие функции.
Шкала роста на бесконечности
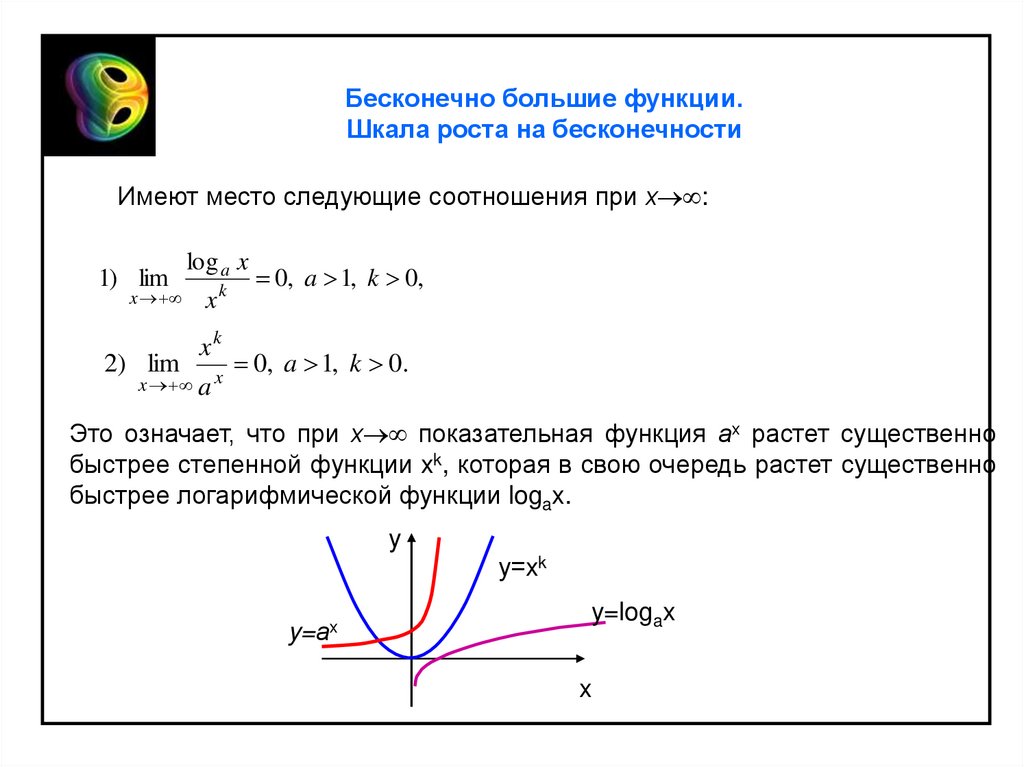
Имеют место следующие соотношения при х :
1) lim
x
2) lim
log a x
x
k
xk
x a x
0, a 1, k 0,
0, a 1, k 0.
Это означает, что при х показательная функция ах растет существенно
быстрее степенной функции xk, которая в свою очередь растет существенно
быстрее логарифмической функции logax.
y
y=ах
у=xk
y=logax
x

65.

Бесконечно большие функции.
Шкала роста на бесконечности
Найдем предел степенно – показательной функции
Имеем неопределенность вида .
Представим
x x e x ln x .
lim x ln x 0
x 0
lim x x e 0 1.
x
lim x x 1.
x
lim x x .
x

66.

Непрерывность функции в точке
Определение 1. Функция y=f(x) называется непрерывной в точке x0, если
выполняются следующие три условия:
1) f(x) определена в точке x0 и в некоторой ее -окрестности;
2) существует конечный предел
lim f ( x);
x x 0
3) предел функции при x x0 равен значению функции f(x0) в точке
x0, т.е. lim f ( x) f ( x0 ).
x x0
Рассмотрим функцию y=f(x) и допустим, что она непрерывна в точке x0, т. е.
lim f ( x) f ( x0 ) lim f ( x) f ( x0 ) lim f ( x) f ( x0 ) 0.
x x0
Обозначения:
x x0
x x0
f (x0) = f (x) – f (x0) - приращением функции в точке х0,
x = x – x0 - приращению аргумента.
Тогда ( lim f ( x) f ( x0 )) ( lim f ( x0 ) 0) и обратно
x x0
x 0
( lim f ( x0 ) 0) ( lim f ( x) f ( x0 )).
x 0
x x0

67.

Непрерывность функции в точке
Таким образом,
( lim f ( x) f ( x0 )) ( lim f 0).
x x0
x 0
Приняв во внимание вышесказанное, можно дать другое определение
непрерывности функции в точке x0.
Определение 2. Функция y=f (x) называется непрерывной в точке x0 ,
если бесконечно малому приращению аргумента в этой точке
соответствует бесконечно малое приращение функции, т. е. если
lim f ( x0 ) 0.
x 0

68.

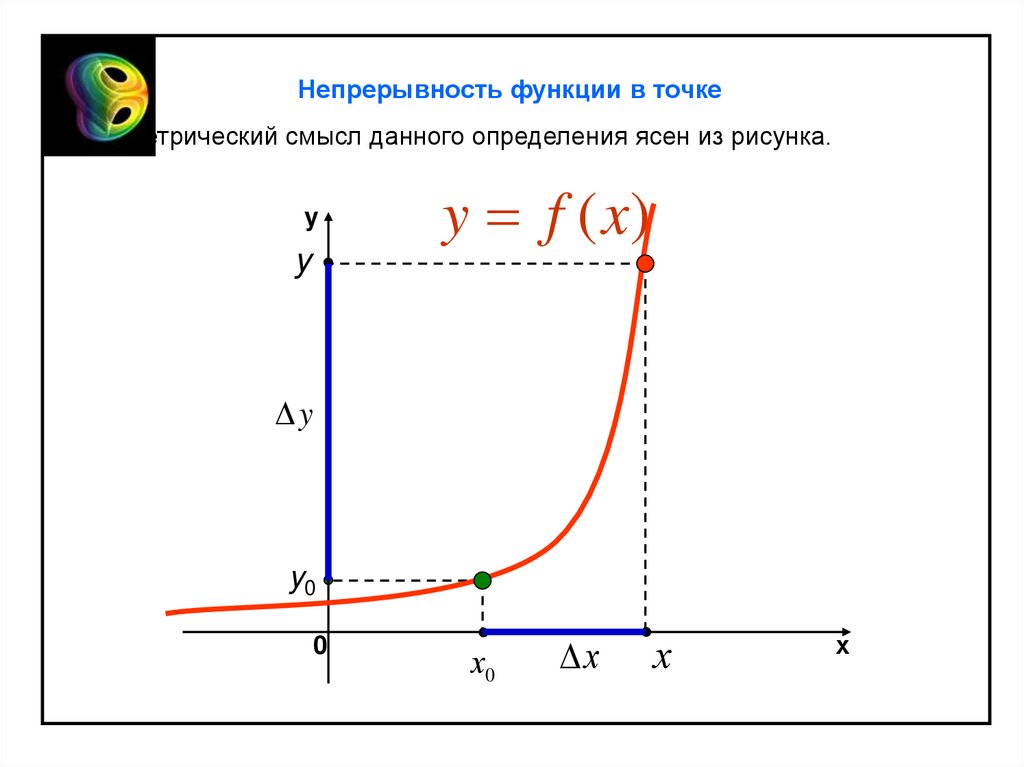
Непрерывность функции в точке
Геометрический смысл данного определения ясен из рисунка.
y
y
y f (x)
y
y0
0
х0
х
х
х

69.

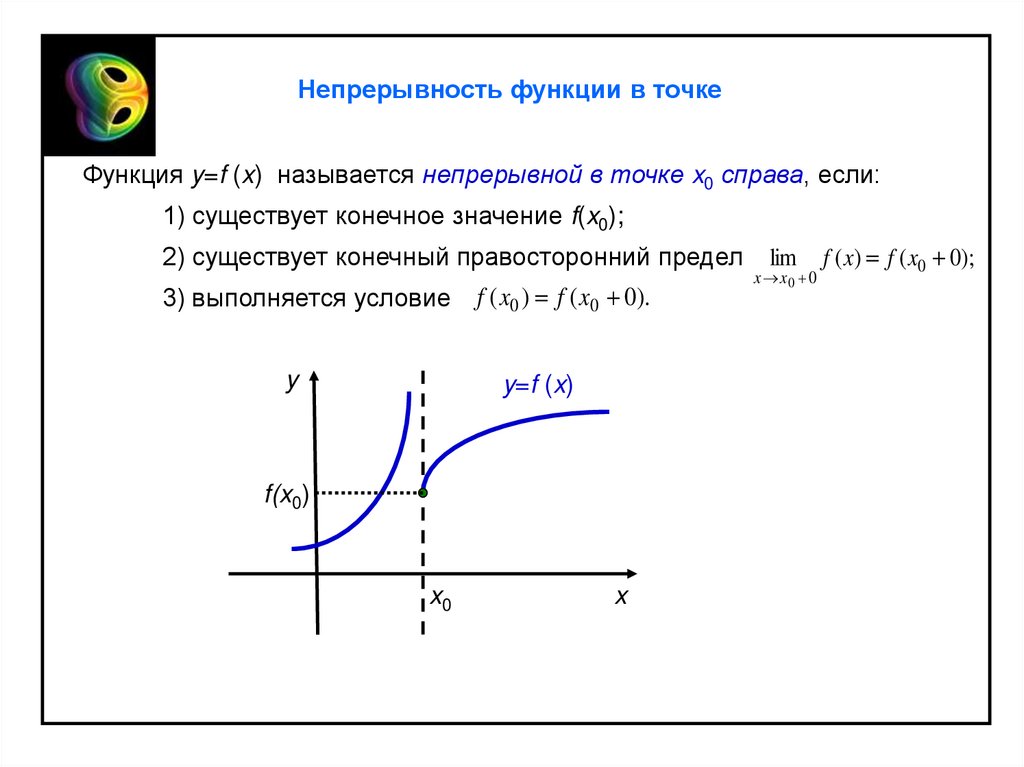
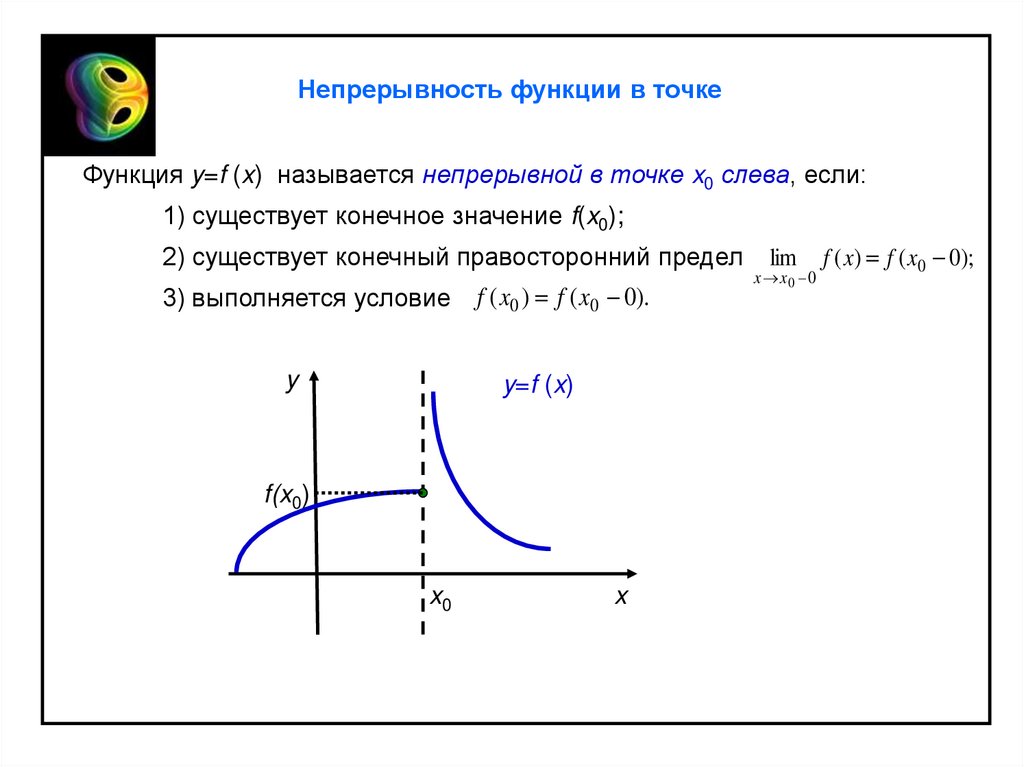
Непрерывность функции в точке
Функция y=f (x) называется непрерывной в точке x0 справа, если:
1) существует конечное значение f(x0);
2) существует конечный правосторонний предел
3) выполняется условие
y
f ( x0 ) f ( x0 0).
y=f (x)
f(x0)
x0
x
lim
x x0 0
f ( x) f ( x0 0);

70.

Непрерывность функции в точке
Функция y=f (x) называется непрерывной в точке x0 слева, если:
1) существует конечное значение f(x0);
2) существует конечный правосторонний предел
3) выполняется условие
y
f ( x0 ) f ( x0 0).
y=f (x)
f(x0)
x0
x
lim
x x0 0
f ( x) f ( x0 0);

71.

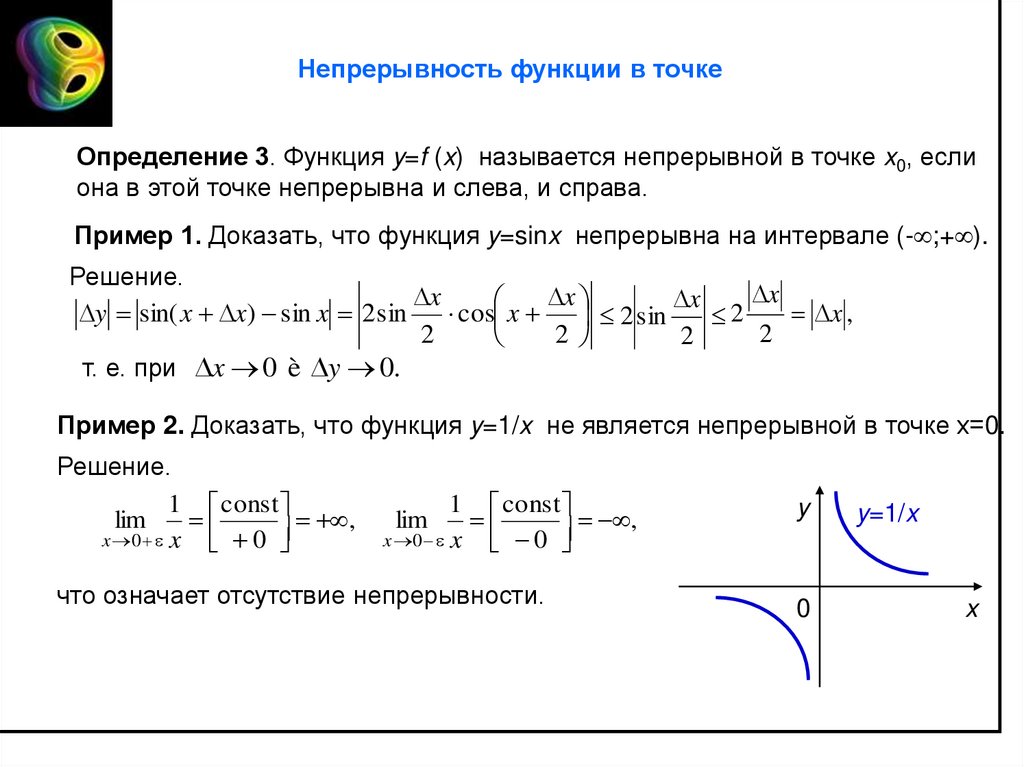
Непрерывность функции в точке
Определение 3. Функция y=f (x) называется непрерывной в точке x0, если
она в этой точке непрерывна и слева, и справа.
Пример 1. Доказать, что функция y=sinx непрерывна на интервале (- ;+ ).
Решение.
x
x
x
x
y sin( x x) sin x 2 sin
2
x ,
cos x
2 sin
2
2
2
2
т. е. при x 0 è y 0.
Пример 2. Доказать, что функция y=1/x не является непрерывной в точке х=0.
Решение.
1 const
lim
,
x 0 x
0
1 const
,
x 0 x
0
lim
что означает отсутствие непрерывности.
y
0
y=1/x
x

72.

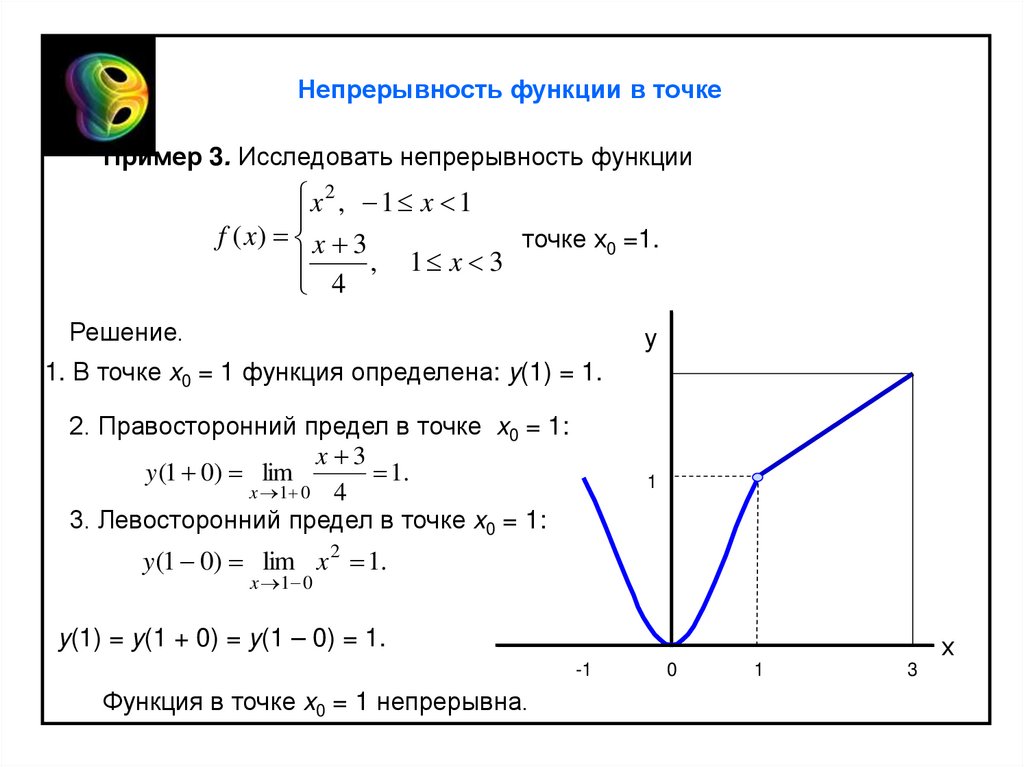
Непрерывность функции в точке
Пример 3. Исследовать непрерывность функции
x 2 , 1 x 1
f ( x) x 3
точке х0 =1.
, 1 x 3
4
Решение.
у
1. В точке x0 = 1 функция определена: y(1) = 1.
2. Правосторонний предел в точке x0 = 1:
x 3
y (1 0) lim
1.
x 1 0 4
3. Левосторонний предел в точке x0 = 1:
1
y (1 0) lim x 2 1.
x 1 0
y(1) = y(1 + 0) = y(1 – 0) = 1.
х
-1
Функция в точке x0 = 1 непрерывна.
0
1
3

73.

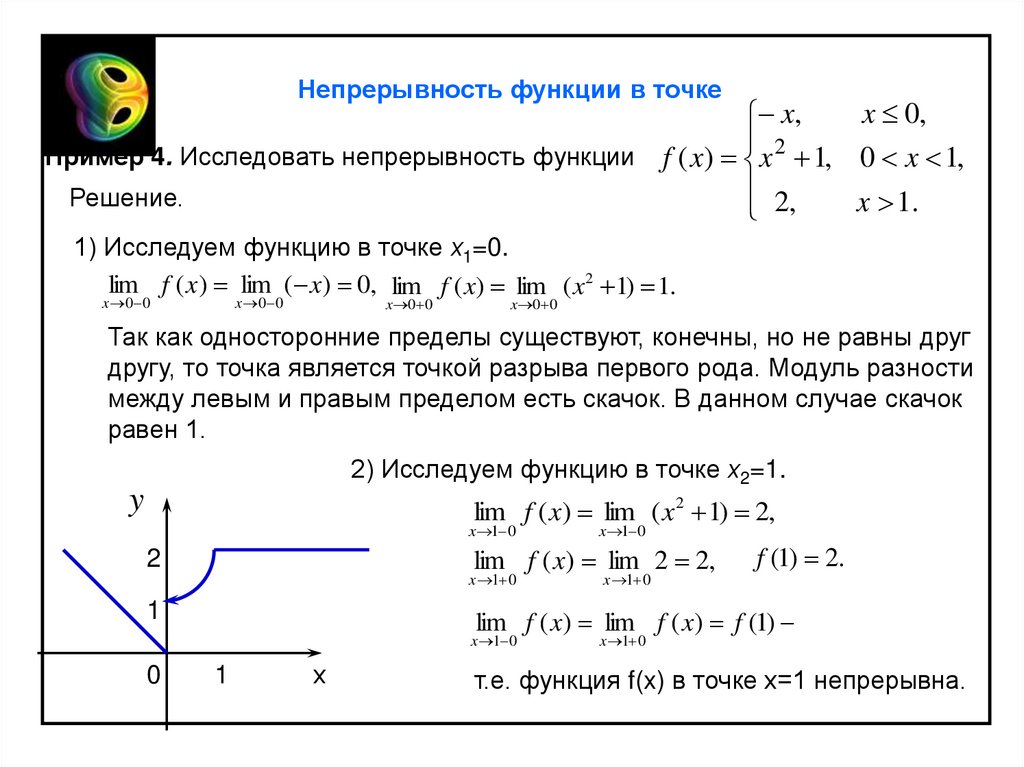
Непрерывность функции в точке
x 0,
x ,
Пример 4. Исследовать непрерывность функции f ( x) x 2 1, 0 x 1,
2,
Решение.
x 1.
1) Исследуем функцию в точке х1=0.
lim f ( x) lim ( x) 0, lim f ( x) lim ( x 2 1) 1.
x 0 0
x 0 0
x 0 0
x 0 0
Так как односторонние пределы существуют, конечны, но не равны друг
другу, то точка является точкой разрыва первого рода. Модуль разности
между левым и правым пределом есть скачок. В данном случае скачок
равен 1.
2) Исследуем функцию в точке х2=1.
y
lim f ( x) lim ( x 2 1) 2,
x 1 0
lim f ( x) lim 2 2,
2
x 1 0
1
x 1 0
f (1) 2.
lim f ( x) lim f ( x) f (1)
x 1 0
0
x 1 0
1
х
x 1 0
т.е. функция f(x) в точке х=1 непрерывна.

74.

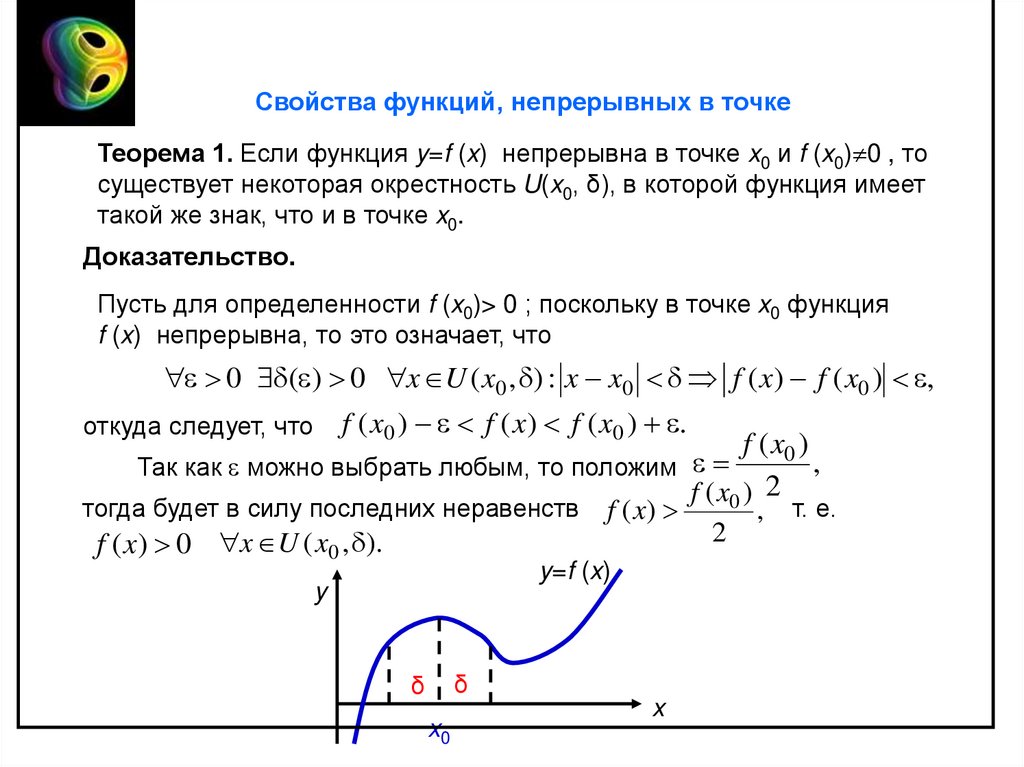
Свойства функций, непрерывных в точке
Теорема 1. Если функция y=f (x) непрерывна в точке x0 и f (x0) 0 , то
существует некоторая окрестность U(x0, δ), в которой функция имеет
такой же знак, что и в точке x0.
Доказательство.
Пусть для определенности f (x0)> 0 ; поскольку в точке x0 функция
f (x) непрерывна, то это означает, что
0 ( ) 0 x U ( x0 , ) : x x0 f ( x) f ( x0 ) ,
f ( x0 ) f ( x) f ( x0 ) .
откуда следует, что
f ( x0 )
,
Так как можно выбрать любым, то положим
f ( x0 ) 2
тогда будет в силу последних неравенств
f ( x) 0 x U ( x0 , ).
f ( x)
y=f (x)
y
δ
δ
x0
x
2
,
т. е.

75.

Свойства функций, непрерывных в точке
Теорема 2. Если функции f1(x) и f2(x) непрерывны в точке x0, то
функции cf1(x), f1(x) f2(x), f1(x) f2(x), f1(x)/ f2(x) (f2(x) 0) непрерывна в точке x0.
Теорема 3 (непрерывность сложной функции). Если функция (x)
непрерывна в точке x0, а функция f(U) непрерывна в точке U0, где
U0 = (x) , то функция f [U(x)] непрерывна в точке x0, т. е. суперпозиция
непрерывных функций непрерывна в данной точке.
Теорема 4 (непрерывность обратной функции). Если функция y = y(x)
строго возрастает (строго убывает) на промежутке [a; b] и непрерывна в
точке x0 ]a; b[, то у нее существует обратная функция x = x(y), которая
строго возрастает (строго убывает) на промежутке
[p; q], где p = y(a),
q = y(b) и непрерывна в точке y0 = y(x0).
Теорема 5. Любая элементарная функция непрерывна в каждой точке ее
множества определения.

76.

Вычисление пределов от непрерывных функций
В силу теоремы о непрерывности элементарных функций следует,
что для каждой элементарной функции имеет место соотношение
lim f ( x) f ( lim x).
x x0
x x0
1
lim
cos
2 .
Пример 1. Найти предел
x
x
Решение.
1
1
lim cos 2 cos lim 2 cos(0) 1.
x
x
x x
x2 2x 1
Пример 2. Найти предел lim ln 2
.
x
3x x 4
Решение.
x2 2x 1
x 2 2 x 1 ln 1 ln 3.
x2 2x 1
lim ln 2
ln lim 2
3
ln lim
2
x
3x x 4
x 3x x 4
x 3x x 4

77.

Свойства функций, непрерывных на отрезке
Определение 1. Функция f (x) , непрерывная в каждой точке отрезка
[a; b], называется непрерывной на этом промежутке.
Под непрерывностью функции на концах промежутка понимается ее
односторонняя непрерывность.
Заметим также, что графиком функции, непрерывной на промежутке,
служит сплошная (непрерывная) линия на этом промежутке, которую
можно вычертить одним движением карандаша, не отрывая его от
бумаги.
Сформулируем теперь достаточно очевидные с геометрической точки
зрения теоремы, дающие нам свойства функций, непрерывных на
промежутке.

78.

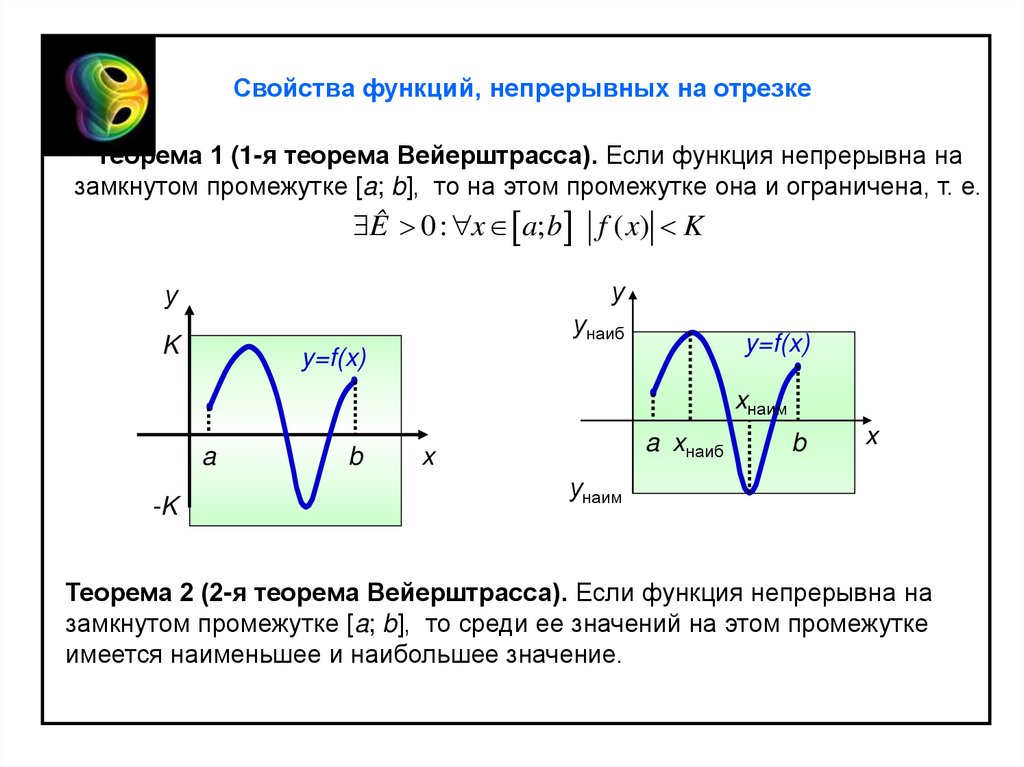
Свойства функций, непрерывных на отрезке
Теорема 1 (1-я теорема Вейерштрасса). Если функция непрерывна на
замкнутом промежутке [a; b], то на этом промежутке она и ограничена, т. е.
Ê 0 : x a; b f ( x) K
у
у
унаиб
K
y=f(x)
y=f(x)
xнаим
a
-K
b
a xнаиб
x
b
x
унаим
Теорема 2 (2-я теорема Вейерштрасса). Если функция непрерывна на
замкнутом промежутке [a; b], то среди ее значений на этом промежутке
имеется наименьшее и наибольшее значение.

79.

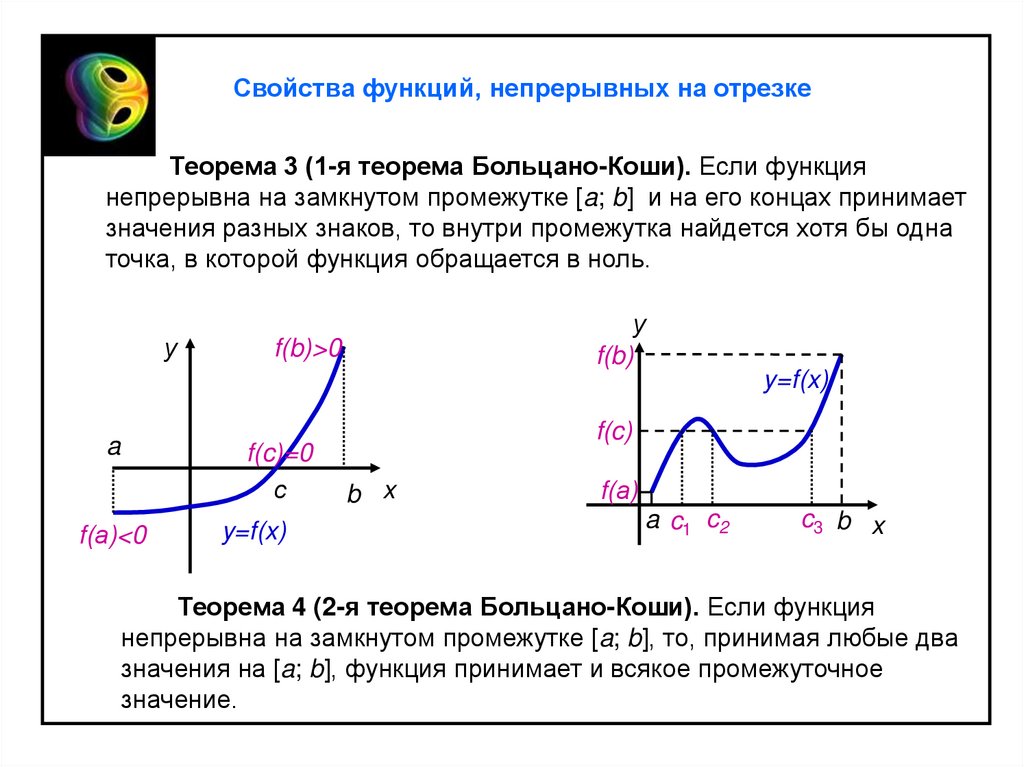
Свойства функций, непрерывных на отрезке
Теорема 3 (1-я теорема Больцано-Коши). Если функция
непрерывна на замкнутом промежутке [a; b] и на его концах принимает
значения разных знаков, то внутри промежутка найдется хотя бы одна
точка, в которой функция обращается в ноль.
у
у
f(b)
f(b)>0
y=f(x)
a
f(c)=0
с
f(а)<0
y=f(x)
f(c)
b x
f(а)
a c1 c2
c3 b x
Теорема 4 (2-я теорема Больцано-Коши). Если функция
непрерывна на замкнутом промежутке [a; b], то, принимая любые два
значения на [a; b], функция принимает и всякое промежуточное
значение.

80.

Свойства функций, непрерывных на отрезке
Cформулировал логическое обоснование
анализа на основе построенной им теории
действительных (вещественных) чисел и
так называемого ε-δ-языка.
Здоровье Вейерштрасса оставляет
желать лучшего. В 1861 году во время
выступления у него начался сильный
приступ головокружения. и пришлось
прервать лекцию. Больше Вейерштрасс
никогда не читал лекции стоя — он
неизменно сидел, а один из лучших
студентов писал за него на доске.

81.

Свойства функций, непрерывных на отрезке
Бернард Больцано
1781 — 1848
чешский математик
При жизни Больцано напечатал анонимно
только пять небольших математических
сочинений. Основная часть большого
рукописного наследия Больцано чешские
ученые исследовали после его смерти.
Большой магматический труд Больцано "Учение
о функциях", написанный в 1830 г., увидел свет
только через сто лет. В нем, в частности,
Больцано (за 30 лет до К.Вейерштрасса) строит
непрерывную кривую, не имеющую касательной
ни в одной точке. Больцано установил
современное понятие сходимости рядов и за
несколько лет до выхода в свет
"Алгебраического анализа" О. Л. Коши
пользовался критерием сходимости,
именуемым обычно критерием Коши. Уточнив
понятия предела и непрерывности, Больцано
впервые строго доказал теорему о том, что
непрерывная функция принимает любое
промежуточное значение, лежащее между
двумя ее разными значениями.

82.

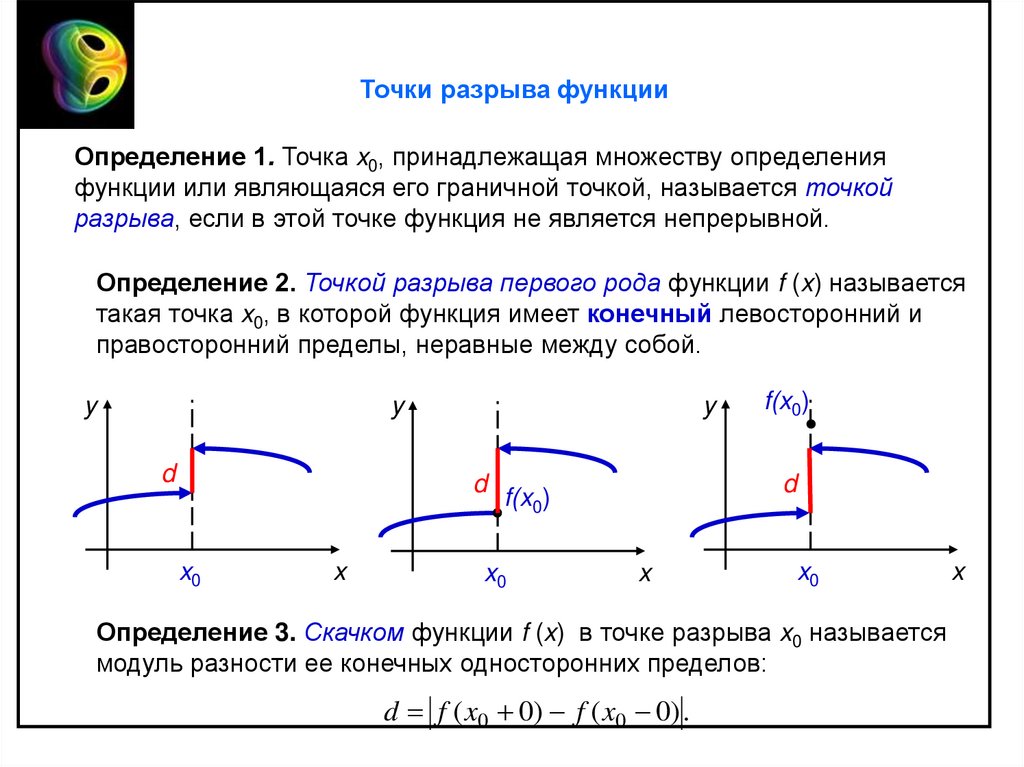
Точки разрыва функции
Определение 1. Точка x0, принадлежащая множеству определения
функции или являющаяся его граничной точкой, называется точкой
разрыва, если в этой точке функция не является непрерывной.
Определение 2. Точкой разрыва первого рода функции f (x) называется
такая точка x0, в которой функция имеет конечный левосторонний и
правосторонний пределы, неравные между собой.
y
y
d
y
d
x0
x
d
f(x0)
x0
f(x0)
x
x0
Определение 3. Скачком функции f (x) в точке разрыва x0 называется
модуль разности ее конечных односторонних пределов:
d f ( x0 0) f ( x0 0) .
x

83.

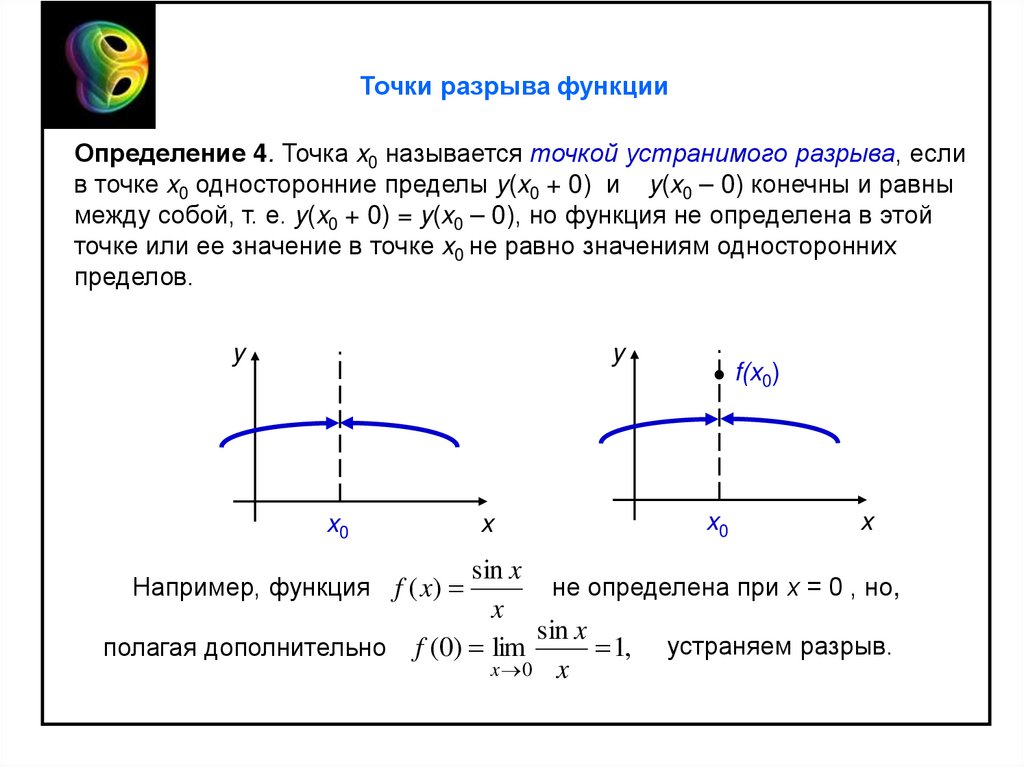
Точки разрыва функции
Определение 4. Точка x0 называется точкой устранимого разрыва, если
в точке x0 односторонние пределы y(x0 + 0) и y(x0 – 0) конечны и равны
между собой, т. е. y(x0 + 0) = y(x0 – 0), но функция не определена в этой
точке или ее значение в точке x0 не равно значениям односторонних
пределов.
y
y
x0
x
x0
x
sin x
не определена при х = 0 , но,
x
sin x
f (0) lim
1, устраняем разрыв.
x 0 x
Например, функция f ( x)
полагая дополнительно
f(x0)

84.

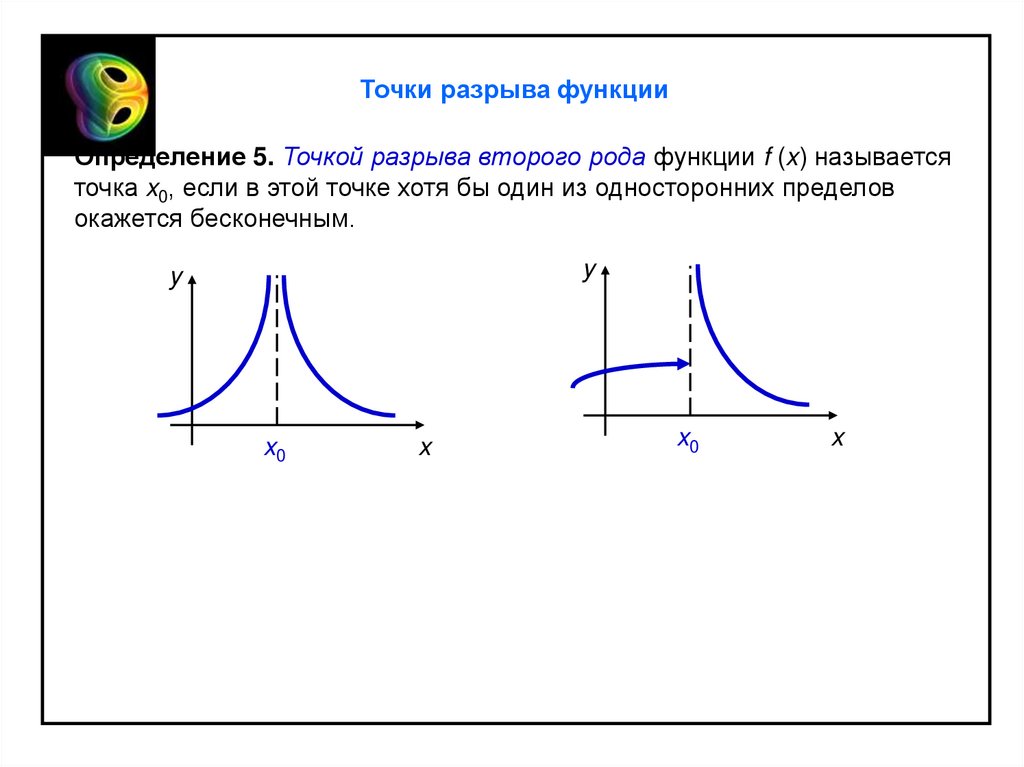
Точки разрыва функции
Определение 5. Точкой разрыва второго рода функции f (x) называется
точка x0, если в этой точке хотя бы один из односторонних пределов
окажется бесконечным.
y
y
x0
x
x0
x

85.

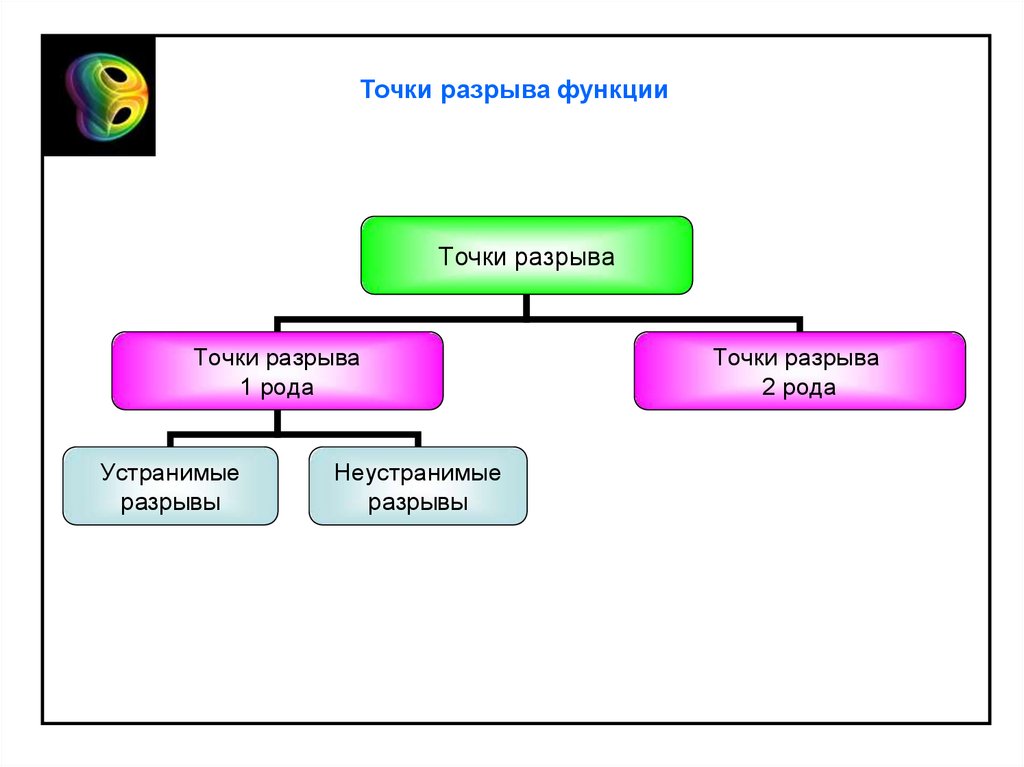
Точки разрыва функции
Точки разрыва
Точки разрыва
1 рода
Устранимые
разрывы
Неустранимые
разрывы
Точки разрыва
2 рода

86.

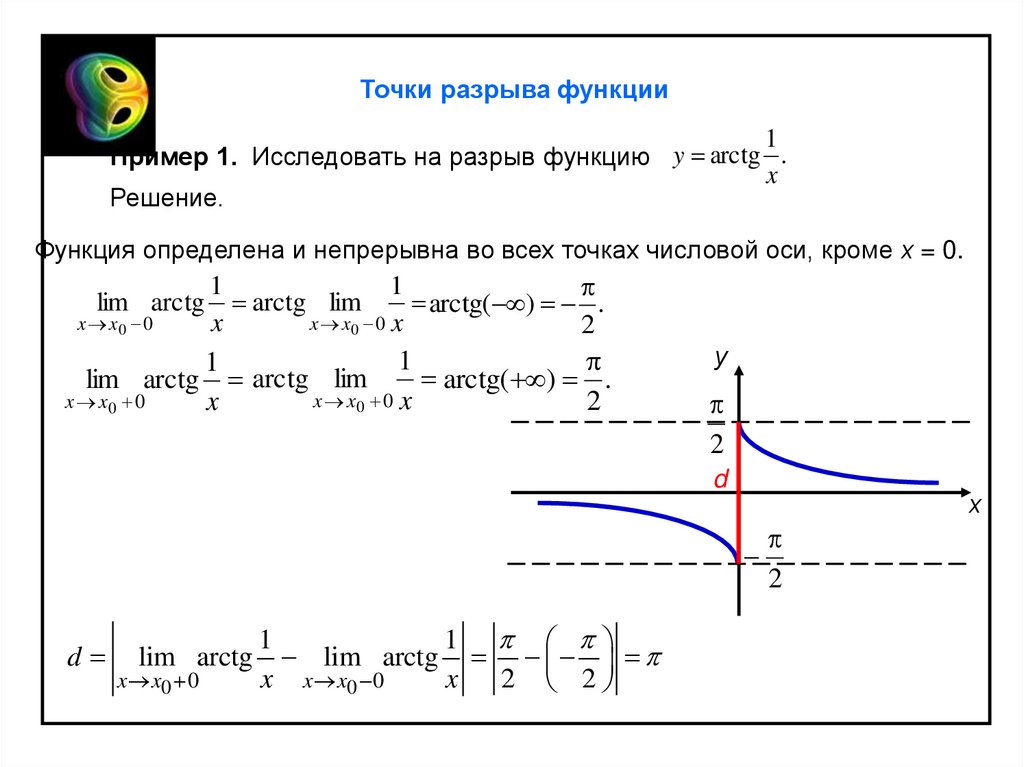
Точки разрыва функции
1
Пример 1. Исследовать на разрыв функцию y arctg .
x
Решение.
Функция определена и непрерывна во всех точках числовой оси, кроме х = 0.
1
1
lim arctg arctg lim
arctg( ) .
x x0 0
x x0 0 x
x
2
у
1
1
arctg( ) .
lim arctg arctg lim
x
x
0
x
2
x
0
x x0 0
2
d
х
d
1
1
lim arctg lim arctg
x x x0 0
x
2 2
x x0 0
2

87.

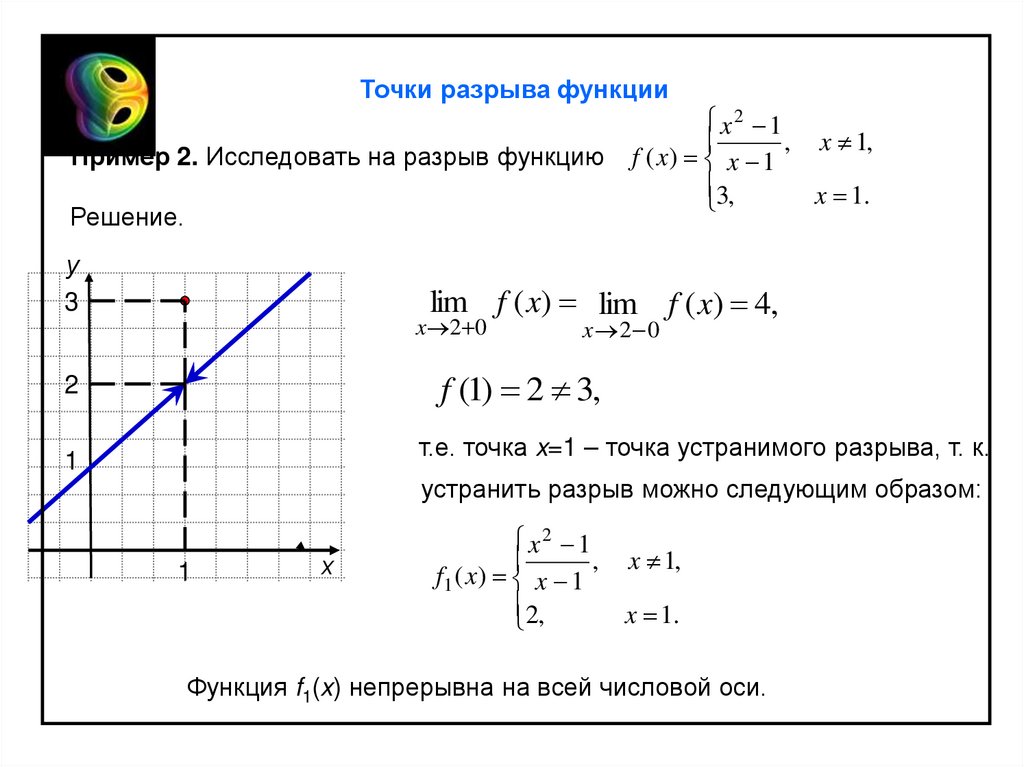
Точки разрыва функции
Пример 2. Исследовать на разрыв функцию
Решение.
у
3
x2 1
, x 1,
f ( x) x 1
3,
x 1.
lim f ( x) lim f ( x) 4,
x 2 0
x 2 0
f (1) 2 3,
2
т.е. точка x=1 – точка устранимого разрыва, т. к.
1
устранить разрыв можно следующим образом:
1
х
x2 1
, x 1,
f1 ( x) x 1
2,
x 1.
Функция f1(x) непрерывна на всей числовой оси.

88.

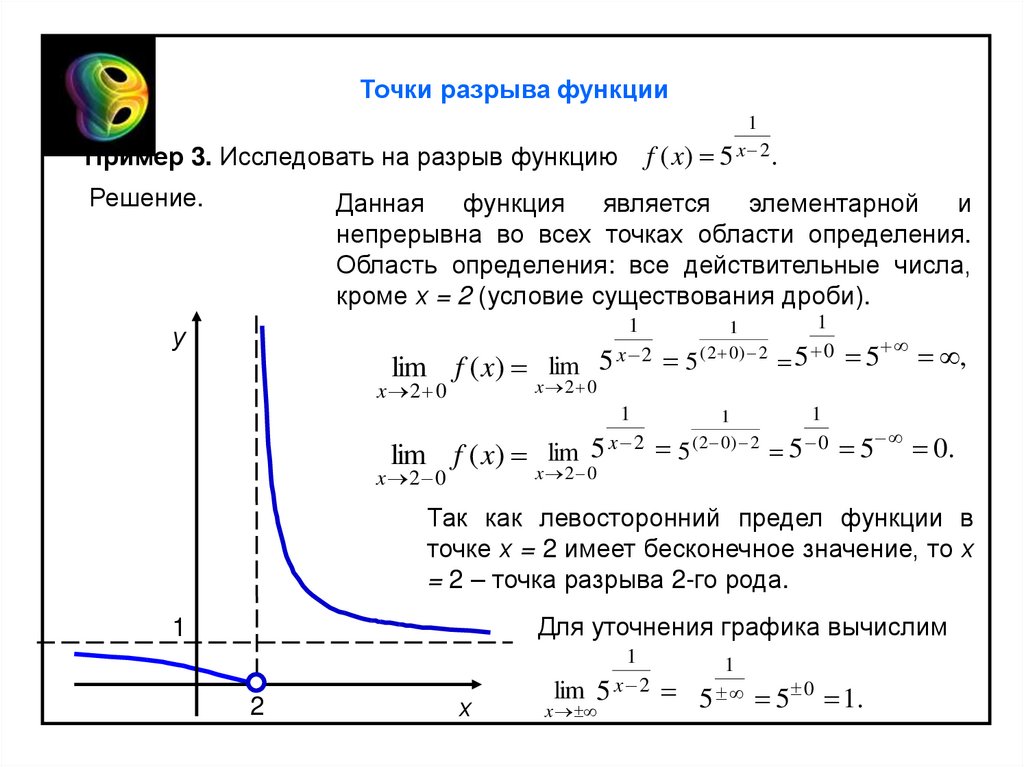
Точки разрыва функции
Пример 3. Исследовать на разрыв функцию
Решение.
1
f ( x) 5 x 2 .
Данная функция является элементарной и
непрерывна во всех точках области определения.
Область определения: все действительные числа,
кроме х = 2 (условие существования дроби).
у
lim f ( x) lim
1
1
1
5 x 2 5 ( 2 0) 2 5 0 5 ,
lim f ( x) lim
1
1
1
5 x 2 5 ( 2 0 ) 2 5 0 5 0.
x 2 0
x 2 0
x 2 0
x 2 0
Так как левосторонний предел функции в
точке х = 2 имеет бесконечное значение, то х
= 2 – точка разрыва 2-го рода.
Для уточнения графика вычислим
1
2
х
1
lim 5 x 2
x
1
5 5 0 1.

89.

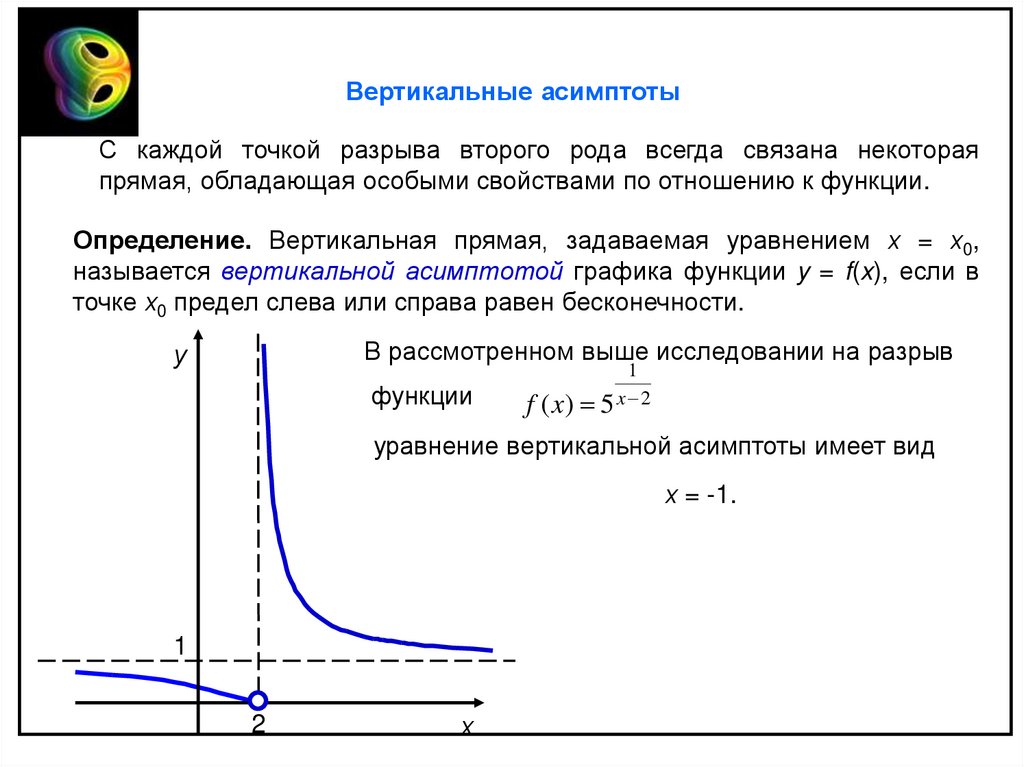
Вертикальные асимптоты
С каждой точкой разрыва второго рода всегда связана некоторая
прямая, обладающая особыми свойствами по отношению к функции.
Определение. Вертикальная прямая, задаваемая уравнением х = х0,
называется вертикальной асимптотой графика функции y = f(x), если в
точке х0 предел слева или справа равен бесконечности.
В рассмотренном выше исследовании на разрыв
у
функции
1
f ( x) 5 x 2
уравнение вертикальной асимптоты имеет вид
х = -1.
1
2
х