Л3_ТЙКС(06.11.25)

1.

1

2.

КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
імені ТАРАСА ШЕВЧЕНКА
Кафедра інформаційних систем та технологій
ТЕОРІЯ ЙМОВІРНОСТЕЙ та КОМП'ЮТЕРНА СТАТИСТИКА
Викладачі: Володимир ДРУЖИНІН; Ганна ТЕРЕЩУК
2025

3.

ЛЕКЦІЯ № 3. Частина 1: «Дискретні і неперервні випадкові величини, їх
розподіли та числові характеристики»
3

4.

1. Види випадкових величин
Випадковою називається величина, яка при кожному проведенні
випробування набуває певного значення з множини можливих значень, причому
заздалегідь невідомо, якого саме.
Відмінність від випадкової події досить істотна: якщо випадкова подія може
або відбутися, або не відбутися в результаті випробування, то випадкова величина
в результаті випробування обов’язково приймає деяке значення.
!!! Можна вважати, що випадкова подія є окремим випадком випадкової
величини, яка приймає тільки два значення – одне, наприклад, 1 – «подія
відбулася», друге 0 – «подія не відбулася».
Таким чином, випадкова подія є якісним вираженням випадкової величини, а
поняття «випадкова величина» є розвиненням, узагальненням поняття «випадкова
подія».
4

5.

!!! Використання випадкових величин дає можливість виконати більш повний,
детальніший аналіз ймовірнісних явищ.
ПРИКЛАД. Якщо в якості випробування розглядати здавання студентом
іспиту, то можна говорити про випадкову подію «студент здав іспит», а можна –
про випадкову величину «отримана оцінка», яка може набути одного зі значень
2, 3, 4, 5.
!!! Очевидно, що величина оцінки дає повнішу інформацію про знання
студента.
5

6.

!!! Випадкові величини можуть бути дискретними і неперервними.
Дискретною випадковою величиною називається така випадкова величина,
число можливих значень якої є скінченною або зліченною множиною.
*** Злічена множина – це така нескінченна множина, елементи якої можна
пронумерувати за допомогою множини натуральних чисел.
!!! Самостійно наведіть приклади дискретних випадкових величин.
6

7.

Дискретні випадкові величини в свою чергу можна поділити на кілька
видів.
1. Кількісна випадкова величина, яка дозволяє кількісно вимірювати
показник за деякою шкалою.
Приклад. Кількість автобусів на лінії, кількість студентів в аудиторії,
кількість необхідного покупцю товару і тому подібне.
7

8.

Ординальна (порядкова) випадкова величина дозволяє тільки
упорядкувати досліджені об’єкти за ступенем виявлення в них аналізованої якості.
*** Такі величини використовуються, коли шкала кількісного вимірювання
відсутня або невідома.
ПРИКЛАД. При дослідженні житлових умов звичайно виділяють групи:
А – погані житлові умови,
Б – задовільні,
В – добрі,
Г – дуже добрі.
8

9.

3. Номінальна (класифікаційна) випадкова величина дозволяє тільки
поділити об’єкти за аналізованою якістю на однорідні групи (класи), що не
піддаються упорядкуванню.
*** Це такі якості як стать студента (хлопець – дівчина), професія
батьків і тому подібне.
9

10.

!!! Найпоширенішим випадком є кількісна випадкова величина і саме такі
величини розглядаються зазвичай в теорії ймовірностей.
10

11.

Неперервною випадковою величиною називається така випадкова
величина, яка може приймати будь-які значення з деякого інтервалу числової осі
(обмеженого чи нескінченного).
ПРИКЛАДИ - час очікування автобуса; розміри деталей, виготовлених
робітником за зміну і інші.
!!! Додати своъ приклади неперервних випадкових величин.
*** При обробці деталей існують допуски на їхні розміри.
Припустимо, що всі деталі відповідають стандарту. Проте їхні розміри є
неперервною випадковою величиною, тому що вони можуть приймати будь-яке значення
всередині заданого інтервалу допуску. Якщо навіть ми одержимо при вимірюванні, що дві
деталі мають однакові розміри, то, підвищивши точність вимірів, ми переконаємося, що
розміри відрізняються в наступному знаку.
!!! Таким чином, всі можливі значення неперервних випадкових величин не
можна пронумерувати за допомогою множини натуральних чисел.
11

12.

Випадкові величини прийнято позначати заголовними (великими) буквами
латинської абетки
Х, Y, Z , ...,
а їх можливі числові значення – відповідними малими літерами:
х1, х2, ..., хn – можливі значення дискретної випадкової величини Х;
y – поточне значення неперервної випадкової величини Y.
12

13.

2. Закон розподілу випадкової величини
У результаті випробування випадкова величина набуває одного зі своїх
можливих значень.
!!! Отже, певну інформацію про випадкову величину можна задати
перерахуванням всіх можливих значень або вказівкою інтервалу можливих
значень.
!!! Але така інформація буде неповною.
ПРИКЛАД. Якщо студент Іваненко старанно вивчав дисципліну протягом всього
семестру, то він скоріш за все отримає оцінку «відмінно».
Якщо ж студент Петренко лише за 5 хвилин до іспиту дізнався, що така дисципліна
вивчалася в цьому семестрі, то він скоріш за все отримає оцінку «незадовільно».
!!! Хоча можливі значення випадкової величини в обох випадках однакові, ймовірність
набуття конкретних значень різна.
13

14.

!!! Для повної характеристики випадкової величини необхідно враховувати як
її можливі значення, так і ймовірності набуття цих значень, що досягається за
допомогою закону розподілу.
Законом розподілу випадкової величини називається будь-яка
відповідність, що встановлює зв’язок між можливими значеннями випадкової
величини і ймовірностями набуття цих значень.
*** Форми завдання закону розподілу можуть бути:
- табличні;
- графічні;
- аналітичні.
14

15.

У випадку дискретної випадкової величини найзручнішою формою закону
розподілу є ряд розподілу.
Він являє собою таблицю, в якій перераховані всі можливі значення
випадкової величини і відповідні їм імовірності:
*** Символом рі позначено ймовірність того, що випадкова величина прийме
своє і-те значення, тобто хі.
Останній факт зазвичай позначають так:
рі = Р(Х = хі ).
15

16.

!!! Ряд розподілу придатний тільки для дискретної випадкової величини,
оскільки для неперервної випадкової величини просто неможливо перерахувати
всі можливі значення.
16

17.

Приклад. По мішені тричі стріляють з рушниці, причому ймовірність
влучення в мішень при кожному пострілі дорівнює 0,7. Випадкова величина Х –
кількість влучень у мішень.
Ряд розподілу випадкової величини в данному випадку буде мати вигляд:
!!! У ряді розподілу – сума ймовірностей, що входять до ряду розподілу,
дорівнює 1.
*** Дійсно, у ряді розподілу повинні бути перераховані всі можливі значення
випадкової величини, тому події
Х = хі (і = 1,2,..., n)
утворюють повну групу несумісних подій, сума ймовірностей яких дорівнює 1.
17

18.

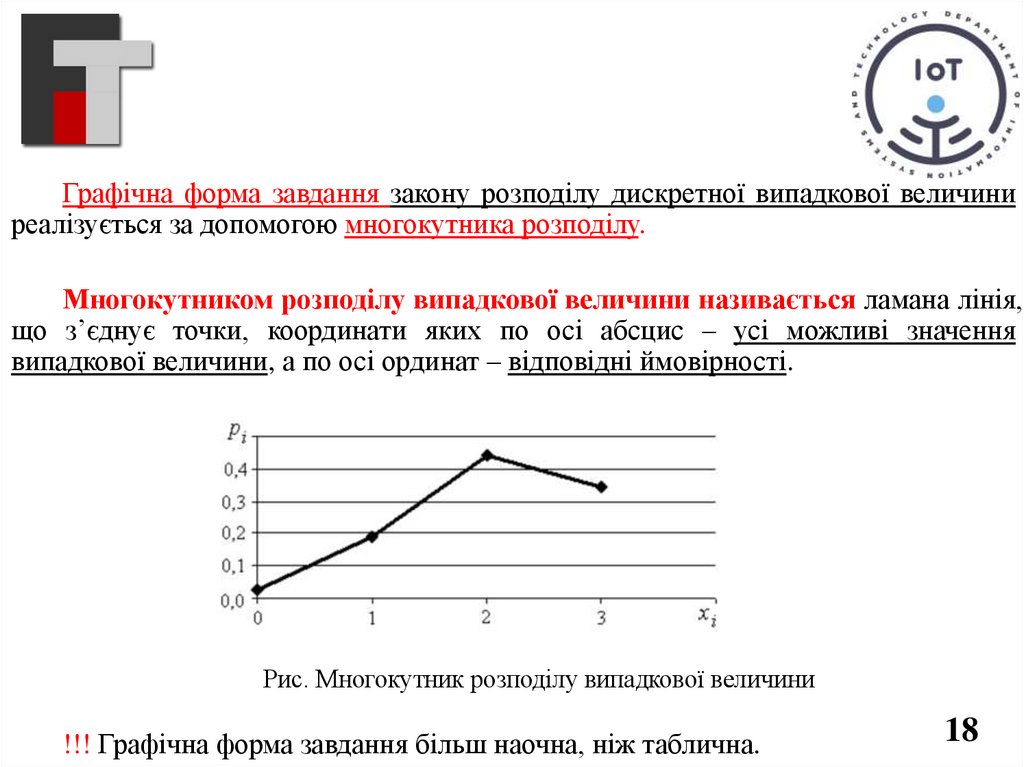
Графічна форма завдання закону розподілу дискретної випадкової величини
реалізується за допомогою многокутника розподілу.
Многокутником розподілу випадкової величини називається ламана лінія,
що з’єднує точки, координати яких по осі абсцис – усі можливі значення
випадкової величини, а по осі ординат – відповідні ймовірності.
Рис. Многокутник розподілу випадкової величини
!!! Графічна форма завдання більш наочна, ніж таблична.
18

19.

Аналітична форма завдання закону розподілу полягає в тому, що задається
аналітичний вираз (формула), за допомогою якої можна обчислити ймовірність рі
для будь-якого значення хі.
*** Так, аналізуючи умову попереднього прикладу (стрільба по мішені), можна
зауважити, що фактично мова йде про схему повторних випробувань Бернуллі, отже у
відповідності з формулою Бернуллі маємо
!!! Одержаний вираз і є аналітичною формою закону розподілу величини Х з
наведеного прикладу, оскільки дає можливість обчислити ймовірність рі для будь-якого
можливого значення
хі = і – 1.
19

20.

3. Функція розподілу та її властивості
*** Ряд розподілу придатний для опису тільки дискретних випадкових величин зі
скінченним числом можливих значень.
Якщо випадкова величина є неперервною або число її можливих значень нескінченне чи
просто велике, то така форма завдання закону розподілу (рядом розподілу) незручна чи
навіть неприйнятна.
!!! У такому випадку застосовують інші форми завдання закону розподілу, зокрема
функція розподілу.
Функцією (інтегральною функцією) розподілу випадкової величини Х називається
функція F(x), що визначає для кожного значення х ймовірність того, що випадкова
величина прийме значення, менше від х:
F(x) = P(X<x)
(1)
20

21.

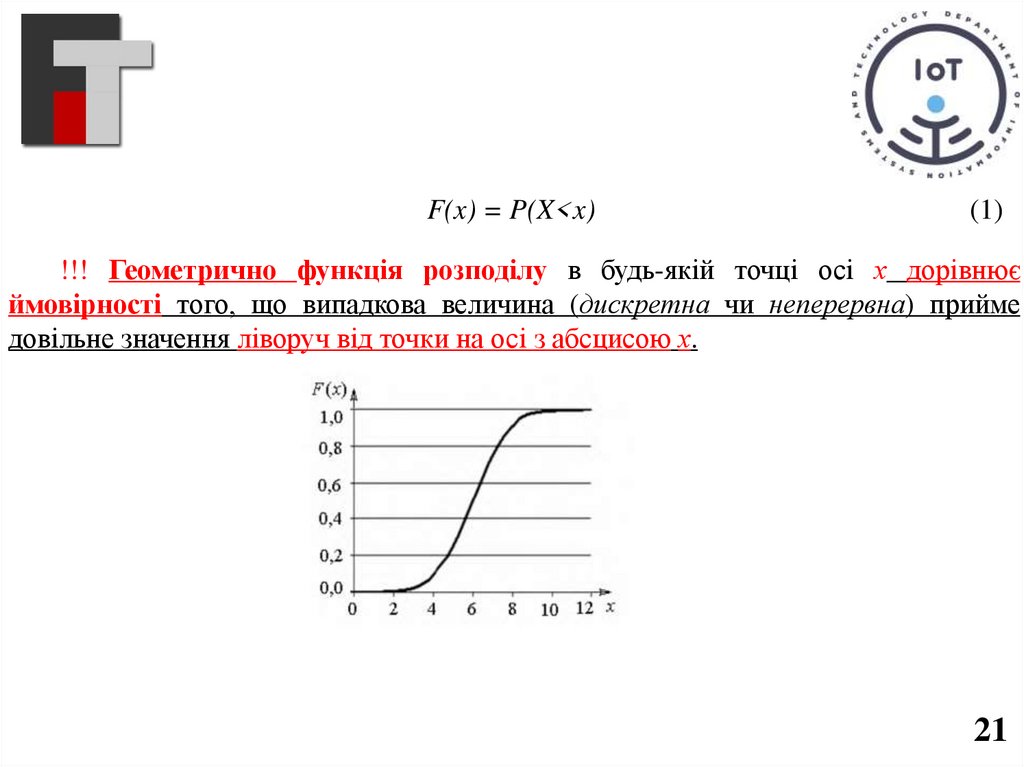
F(x) = P(X<x)
(1)
!!! Геометрично функція розподілу в будь-якій точці осі х дорівнює
ймовірності того, що випадкова величина (дискретна чи неперервна) прийме
довільне значення ліворуч від точки на осі з абсцисою х.
21

22.

!!! Користуючись визначенням функції F(x), можна обчислити ймовірність
того, що випадкова величина прийме значення, яке належить інтервалу [a, b).
*** Для цього розглянемо три події:
А – випадкова величина набула значення Х < а,
В – випадкова величина набула значення Х < b,
С – випадкова величина набула значення а ≤ X < b.
Подія В відбудеться, якщо з’явиться будь-яка з подій А чи С, отже
В = А+С.
Події А і С несумісні, отже
Р(В)=Р(А)+Р(С).
22

23.

*** Виразимо імовірності подій через функцію розподілу.
Р(В)=Р(Х< b)=F(b);
P(A)=P(X<a)=F(a);
P(a ≤ X<b)=P(C)=P(B)–P(A)=F(b)–F(a) .
!!! Таким чином, остаточно маємо
P(a ≤ X<b)= F(b)–F(a)
(2)
23

24.

З формул (1) – (2) витікають такі властивості функції розподілу:
то
1. Значення функції розподілу належать інтервалу [0, 1], тобто
0 ≤ F(x) ≤ 1.
2. Функція розподілу – неспадна функція, тобто, якщо
х2 > х1, то
F(х2) > F(х1).
3. Якщо всі можливі значення випадкової величини належать інтервалу [a,b],
F(x) = 0 при х < а
і
F(x) = 1 при х > b.
4. Якщо можливі значення випадкової величини належать всій числовій осі, то
функція розподілу на мінус нескінченності прямує до нуля, на плюс нескінченності
прямує до одиниці, тобто.
24

25.

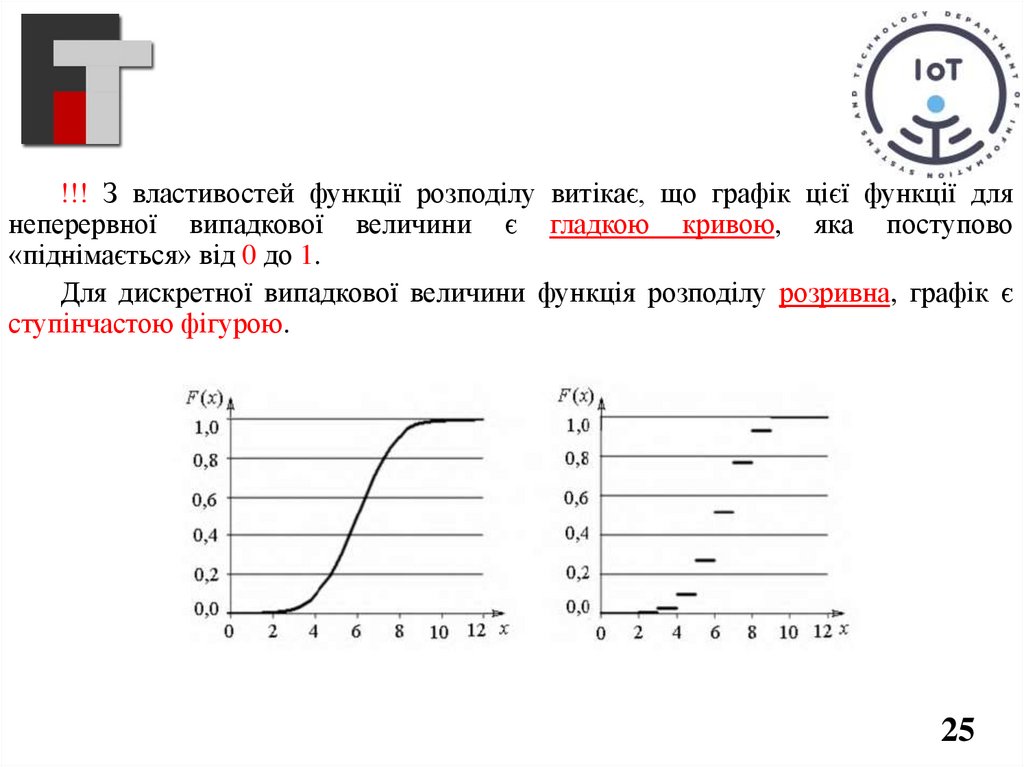
!!! З властивостей функції розподілу витікає, що графік цієї функції для
неперервної випадкової величини є гладкою кривою, яка поступово
«піднімається» від 0 до 1.
Для дискретної випадкової величини функція розподілу розривна, графік є
ступінчастою фігурою.
25

26.

4. Властивість неперервної випадкової величини
P(a ≤ X<b)= F(b)–F(a)
(2)
*** З формули (2) витікає цікава властивість неперервної випадкової
величини.
Дійсно, якщо випадкова величина Х неперервна, то приріст функції F(x) в
точці дорівнює нулю і, звужуючи інтервал [a, b) до точки, одержимо
!!! Таким чином, ймовірність того, що неперервна випадкова величина
набуде одного якогось конкретного значення, дорівнює нулю.
26

27.

!!! Слід зауважити, що врахування розглянутої вище властивості дозволяє для
неперервної випадкової величини формулу (2)
P(a ≤ X<b)= F(b)–F(a)
(2)
подати і у вигляді наданому нижче:
(3)
(4)
27

28.

5. Щільність розподілу випадкової величини та її властивості
*** Функція розподілу є інтегральною характеристикою, по якій важко судити про
характер розподілу випадкової величини в околі тієї чи іншої точки числової осі.
Це добре видно при порівнянні многокутнику розподілу і графіку функції розподілу.
!!! Про особливості поведінки випадкової величини в околі кожного значення наочніше
свідчить многокутник.
Але ця характеристика придатна тільки для дискретних випадкових величин.
*** З вищої математики відомо, що локальні особливості поведінки функції в околі
точки можуть бути описані похідною, що робить доцільним введення щільності
розподілу або диференціальної функції розподілу.
28

29.

Щільністю розподілу неперервної випадкової величини називається
границя відношення ймовірності попадання неперервної випадкової величини на
елементарний відрізок до довжини цього відрізку, коли останній прямує до
Оскільки
то можна стверджувати, що щільність розподілу дорівнює похідній від
функції розподілу
(5)
29

30.

Властивості щільності розподілу випадкової величини.
1. Щільність розподілу невід’ємна функція.
Дійсно, щільність розподілу є похідною неспадної функції F(х), а похідна від’ємна
тільки на інтервалі спадання функції.
2. Ймовірність того, що неперервна випадкова величина Х прийме значення,
яке належить інтервалу (а, b), дорівнює визначеному інтегралу від щільності
розподілу, узятому в межах від а до b
(6)
3. Інтеграл від щільності розподілу у нескінченних межах дорівнює 1
(7)
30

31.

!!! Якщо всі можливі значення неперервної випадкової величини належать
інтервалу (а, b), то
(8)
4. Якщо відома щільність розподілу f(x), то функцію розподілу F(х) можна
знайти зі співвідношення
(9)
*** Дійсно, враховуючи формули (1), (6) маємо
31

32.

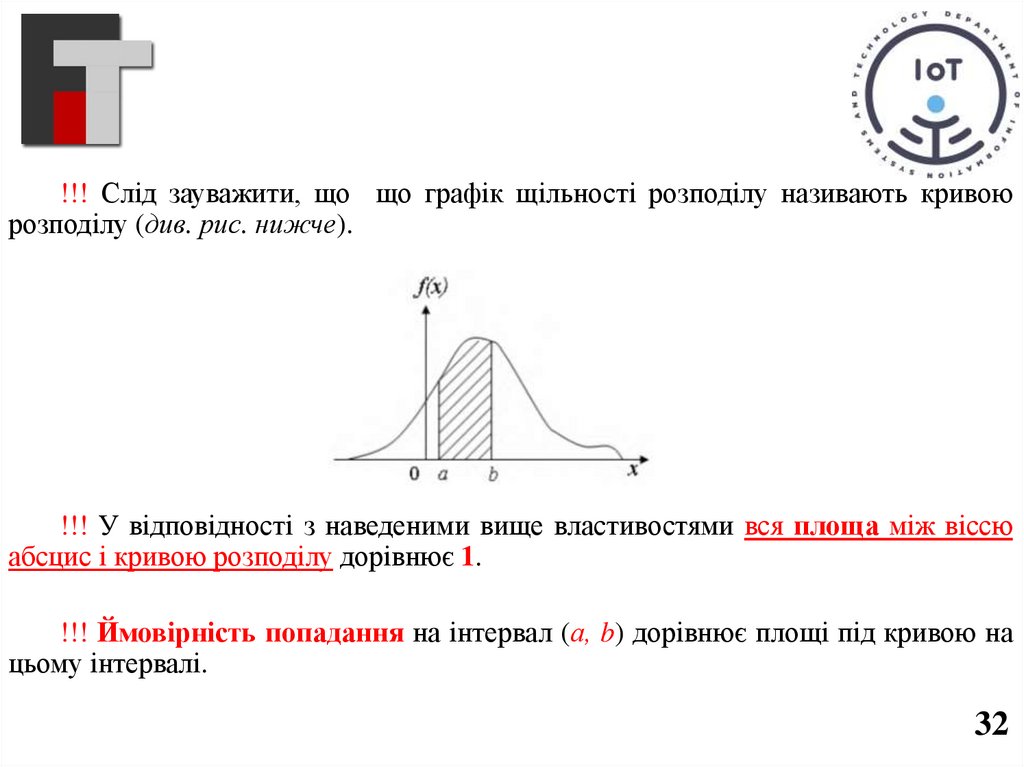
!!! Слід зауважити, що що графік щільності розподілу називають кривою
розподілу (див. рис. нижче).
!!! У відповідності з наведеними вище властивостями вся площа між віссю
абсцис і кривою розподілу дорівнює 1.
!!! Ймовірність попадання на інтервал (а, b) дорівнює площі під кривою на
цьому інтервалі.
32

33.

6. Числові характеристики випадкових величин. Мода і медіана
Випадкова величина вважається заданою, якщо визначено закон її розподілу
в будь-якій його формі – рядом розподілу, функцією або щільністю розподіл.
!!! Однак можуть використовуватися, і в дійсності застосовуються набагато
частіше, спрощені форми представлення випадкових величин – числові характеристики
розподілу.
!!! У загальному випадку вони не задають нам закон розподілу, а тільки
характеризують деякі, найбільш характерні його риси.
*** В окремих випадках, якщо припустити той чи інший закон розподілу, дві чи
навіть одна числова характеристики можуть цілком характеризувати розподіл
випадкової величини.
33

34.

Серед числових характеристик виділяють характеристики положення та
характеристики розсіювання.
Перші характеризують положення випадкової величини на числовій осі,
другі – розсіяння можливих значень відносно центру розподілу.
До характеристик положення відносять моду, медіану і математичне
очікування,
до характеристик
відхилення.
розсіяння
–
дисперсію
та
середнє
квадратичне
34

35.

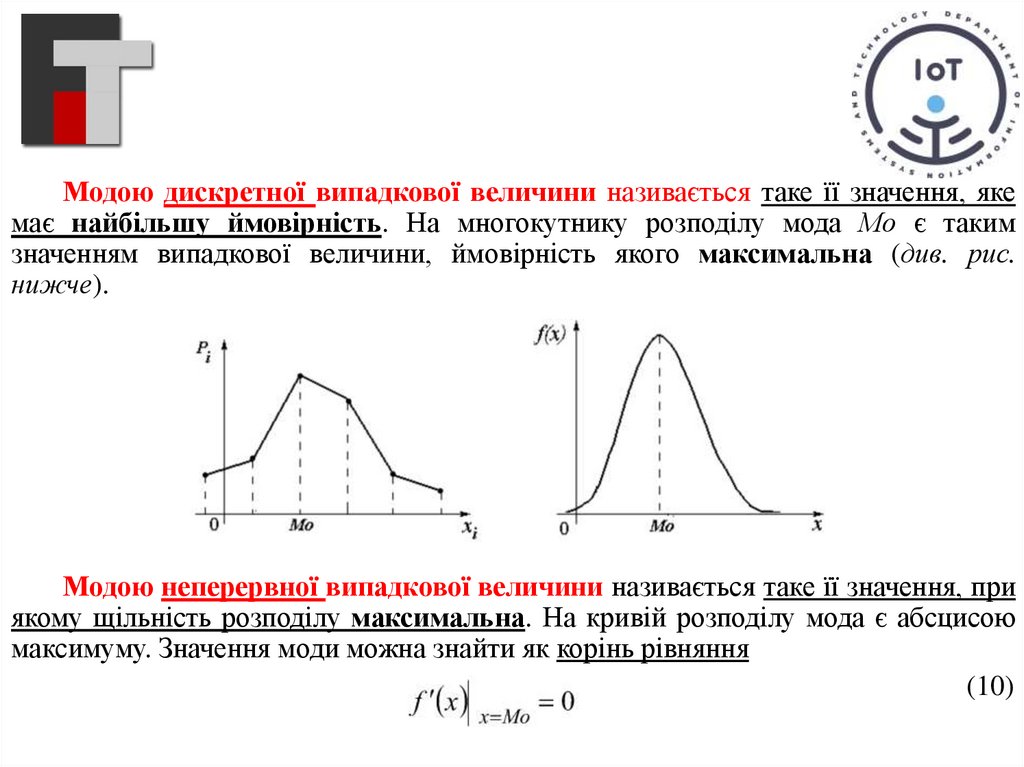
Модою дискретної випадкової величини називається таке її значення, яке
має найбільшу ймовірність. На многокутнику розподілу мода Мо є таким
значенням випадкової величини, ймовірність якого максимальна (див. рис.
нижче).
Модою неперервної випадкової величини називається таке її значення, при
якому щільність розподілу максимальна. На кривій розподілу мода є абсцисою
максимуму. Значення моди можна знайти як корінь рівняння
(10)

36.

Розподіл випадкових величин може бути
одномодальним (унімодальним),
двомодальним,
багатомодальним
в залежності від кількості максимумів на многокутнику чи кривій розподілу.
Наприклад, наведені на рис. слайду №35 розподіли є одномодальними, а розподіл
кількості покупців у магазині протягом дня чи кількості відвідувачів студентської їдальні
протягом дня – багатомодальні розподіли.
*** Іноді можна зустріти термін – антимодальний розподіл;
це такий розподіл, крива розподілу якого має мінімум, а максимальні значення
розташовані на границях інтервалу.
36

37.

Медіана (Ме) - це абсциса точки, в якій площа під кривою розподілу
поділяєтьсяч навпіл.
*** Виходячи з наведеного означення для дискретних випадкових величин не
завжди можна однозначно вказати медіану.
В зв’язку з цим на практиці медіана як числова характеристика набула
поширення лише для неперервних випадкових величин.
Отже, за означенням
P(X < Me) = P(X > Me).
Врахуємо, що P(X < Me) = F(Ме), сума вказаних вище ймовірностей
дорівнює 1, а кожна з них дорівнює 0,5, і остаточно одержимо формулу для
визначення медіани неперервної випадкової величини.
(11)
37

38.

7. Математичне очікування та його властивості
Математичним
очікуванням
дискретної
випадкової
величини
називається сума добутків усіх можливих значень випадкової величини на
ймовірності цих значень
(12)
Математичне очікування неперервної випадкової величини, всі значення
якої знаходяться на інтервалі (a, b), обчислюється за формулою
(13)
38

39.

!!! Математичне очікування завжди має ту ж розмірність, що і досліджувана
величина.
!!! Інші назви математичного очікування – середнє значення або центр
розподілу.
*** Широке застосування математичного очікування якраз і зумовлене тим, що
розраховане до випробування М(Х) наближено дорівнює середньому значенню
зареєстрованих в випробуваннях значень випадкової величини, причому точність
наближення зростає при збільшенні кількості випробувань.
!!! Таким чином, з’являється можливість прогнозувати результат випробувань.
*** Вважається, що сам термін «математичне очікування» виник в зв’язку зі застосуванням
ймовірнісних методів в страхуванні, коли необхідно було визначити очікувану (передбачувану)
величину виплат за договорами страхування.
39

40.

Математичне очікування випадкової величини є невипадковою сталою
величиною, яка залежить тільки від закону розподілу.
*** Це пояснюється тим, що М(Х) є узагальненою характеристикою.
!!! Математичне очікування може не співпадати з жодним зі значень
дискретної випадкової величини.
40

41.

Для математичного очікування характерний ряд властивостей, основними з
яких є такі.
1. Математичне очікування постійної величини дорівнює самій постійній
величині:
М(С) = С.
*** Дійсно, сталу величину можна розглядати як випадкову величину, яка з
імовірністю 1 приймає своє єдине значення.
2. Математичне очікування суми двох випадкових величин дорівнює сумі їх
математичних очікувань.
M(X+Y)= M(X) + M(Y) .
41

42.

НАСЛІДОК. Математичне очікування суми постійної і випадкової величини
дорівнює сумі постійної величини і математичного очікування випадкової
величини
М(С+Х) = С+М(Х)
3. Математичне очікування добутку двох незалежних випадкових величин
дорівнює добутку їх математичних очікувань.
М(XY) = M(X)∙M(Y).
НАСЛІДОК.
очікування
Сталий множник можна виносити за знак математичного
М(С∙Х)= С ∙М(Х).
!!! Друга і третя властивості математичного сподівання справедливі при будь42
якій кількості доданків чи множників.

43.

8. Характеристики розсіяння випадкової величини
Математичне очікування випадкової величини дає вірне уявлення про її
середньозважене значення – центр розподілу.
!!! Однак, для повної характеристики випадкової величини цього мало.
!!! Дві випадкові величини можуть мати однакові математичні очікування, але
зовсім різне розсіяння навколо центра розподілу.
Наприклад, при стрільбі по мішені майстра спорту зі стрільби і простого студента
центр розсіювання мало відрізняється від правильного – від яблучка, але в майстра кулі
лягають купчасто, у студента – істотно розсіюються.
Середній вік студентів і жителів міста може бути однаковим (наприклад, 21 рік),
але розкид, розсіювання цих двох випадкових величин різне – у студентів вік від 17 до 25
років, у жителів міста – від дитячого віку до пенсійного.
!!! Найчастіше для характеристики розсіяння випадкової величини Х
відносно центру розподілу використовується дисперсія.
43

44.

Дисперсією випадкової величини називається математичне очікування
квадрата відхилення випадкової величини від її математичного очікування.
*** Позначимо для стислості
М(Х) = а,
тоді у відповідності з означенням вище маємо
(14)
а формули для обчислення дисперсії дискретної і неперервної випадкових
величин, приймають вид
(15)
(16)
44

45.

Властивості дисперсії.
1. Дисперсія постійної величини дорівнює нулю:
2. Сталий множник можна виносити за знак дисперсії в квадраті:
D(СX) =
3. Дисперсія суми двох незалежних випадкових величин дорівнює сумі
дисперсій цих величин:
D(X+Y) = D(X)+D(Y)
45

46.

Наслідок. Дисперсія суми сталої і випадкової величини дорівнює
дисперсії випадкової величини:
D(X+С)=D(X)+D(С)= D(X)
4. Дисперсія різниці двох незалежних випадкових величин дорівнює сумі їх
дисперсій:
D(X - Y) = D(X)+D(Y)
5. Дисперсія дорівнює різниці між математичним очікуванням квадрата
випадкової величини Х і квадратом її математичного сподівання:
46

47.

!!! Остання властивість дозволяє записати дещо інші формули для
обчислення дисперсії дискретних і неперервних випадкових величин:
(17)
(18)
*** Формули (17) – (18) в багатьох випадках зручніші, ніж формули (15 – (16). Якщо,
наприклад, хі – дискретна випадкова величина, що приймає цілі значення, а величина М(Х) = а –
дробова, то числення за формулою (17) набагато простіші, ніж за формулою (15), тому що до
квадрату треба підносити цілі числа.
Крім того, обчислення за формулами (17)–(18) простіші в програмуванні та при обчисленнях в
таблицях.
47

48.

!!! Дисперсія випадкової величини має розмірність, що дорівнює квадрату
розмірності випадкової величини.
*** Це не завжди зручно для користування, тому на практиці частіше
використовують як міру розсіяння середнє квадратичне відхилення
σх
(в середовищі MS Excel – стандартний відхил), яке обчислюється за
формулою
(19)
!!! Наведені вище властивості дисперсії можуть бути поширені (з відповідною
зміною) на середнє квадратичне відхилення.
48

49.

!!! Інколи застосовуються і інші характеристики розсіяння, наприклад,
середній абсолютний відхил від центра
!!! Однак ця характеристика незручна для теоретичних досліджень і тому
застосовується дуже рідко.
!!! Ще рідше застосовується розмах розподілу – різниця між максимальним
і мінімальним значеннями випадкової величини.
49

50.

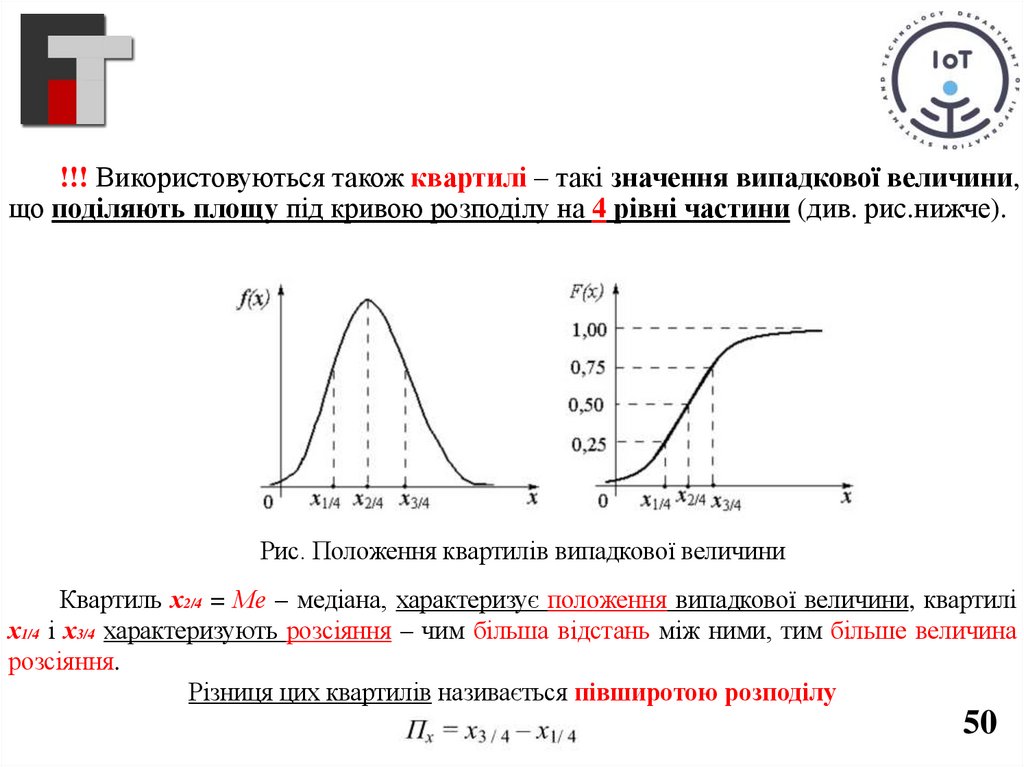
!!! Використовуються також квартилі – такі значення випадкової величини,
що поділяють площу під кривою розподілу на 4 рівні частини (див. рис.нижче).
Рис. Положення квартилів випадкової величини
Квартиль х2/4 = Ме – медіана, характеризує положення випадкової величини, квартилі
х1/4 і х3/4 характеризують розсіяння – чим більша відстань між ними, тим більше величина
розсіяння.
Різниця цих квартилів називається півширотою розподілу
50

51.

9. Моменти випадкових величин
В теорії ймовірностей моменти випадкових величин є узагальненим
вираженням числових характеристик.
Моменти випадкових величин поділяють на початкові і центральні.
Початковим моментом k-го порядку випадкової величини Х називається
математичне очікування k-го степеня Х, тобто
(20)
51

52.

Для дискретної і неперервної випадкових величин формули для обчислення
початкових моментів мають вид
(21)
!!! Очевидно, що математичне очікування дорівнює початковому моменту
першого порядку, а дисперсія дорівнює різниці початкового моменту другого
порядку і квадрату початкового моменту першого порядку:
Центральним моментом k-го порядку називають математичне сподівання kго степеня відхилення випадкової величини від її математичного сподівання
(22)
52

53.

Для дискретної і неперервної випадкових величин формули для обчислення
центральних моментів мають вид .
!!! Центральний момент першого порядку дорівнює нулю;
центральний момент другого порядку дорівнює дисперсії випадкової
величини:
53

54.

!!! Якщо розподіл (як дискретний, так і неперервний) симетричний, то
математичне очікування дорівнює медіані.
В цьому випадку щільність розподілу f(х) буде парною функцією відносно
прямої
х = М(Х) = Ме = а
і всі центральні моменти непарних порядків дорівнюють нулю.
!!! Відмінність непарних моментів від нуля може слугувати кількісною мірою
асиметрії розподілу.
54

55.

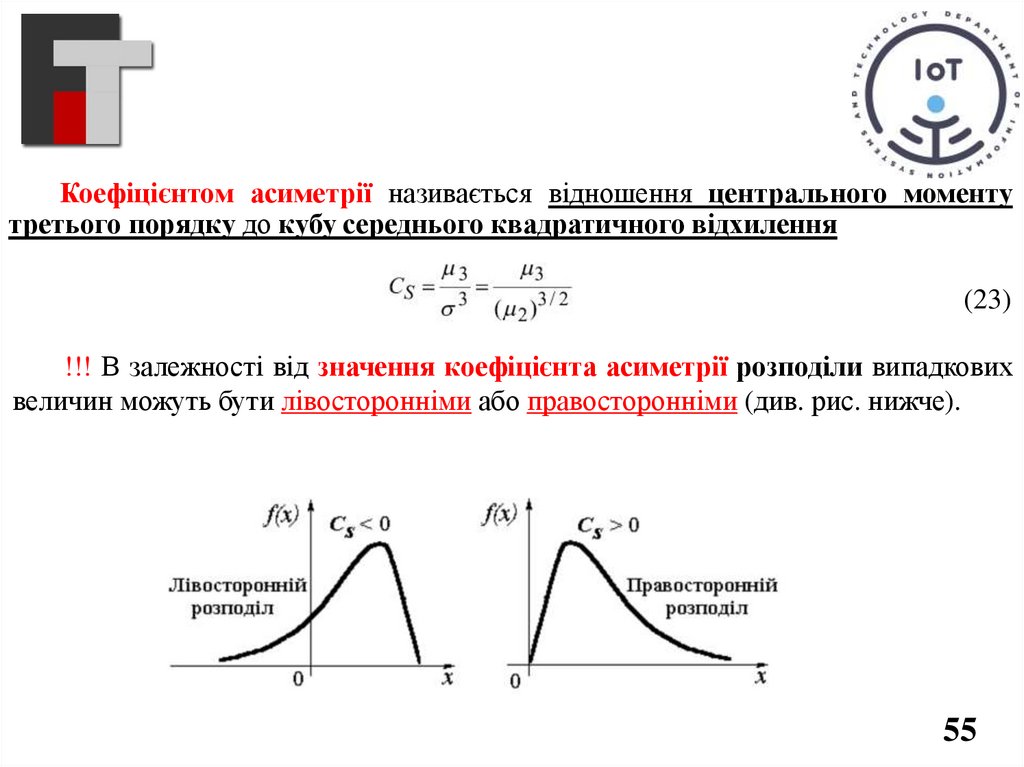
Коефіцієнтом асиметрії називається відношення центрального моменту
третього порядку до кубу середнього квадратичного відхилення
(23)
!!! В залежності від значення коефіцієнта асиметрії розподіли випадкових
величин можуть бути лівосторонніми або правосторонніми (див. рис. нижче).
55

56.

!!! Ще однією числовою характеристикою випадкових величин є коефіцієнт
ексцесу, який обчислюється за формулою
(24)
!!! Для найбільш розповсюдженого для випадкових величин нормального розподілу
коефіцієнт ексцесу дорівнює нулю.
!!! Для розподілів, криві яких більше згладжені в порівнянні з нормальним
розподілом, коефіцієнт ексцесу менше нуля (на рис. нижче нормальний розподіл
показаний пунктирною лінією).
!!! Якщо для якогось розподілу Еx > 0, то крива такого розподілу більше
гостровершинна, ніж крива нормального розподілу.
56

57.

Контрольні питання
1. Дати означення випадкової величини. Чим випадкова величина
відрізняється від випадкової події?
2. Які види випадкових величин використовуються в економічних
дослідженнях, в чому їх особливості?
3. Що таке закон розподілу? В яких формах він може бути заданий?
4. Дати означення функції розподілу та вказати її властивості.
5. Дати означення щільності розподілу та вказати її властивості.
6. Для чого використовуються числові характеристики розподілів? Які з них
відносяться до характеристик положення, а які – до характеристик розсіяння?
7. Дати означення моди та описати процедуру її визначення для дискретних і
неперервних випадкових величин.
57

58.

Контрольні питання
8. Дати означення медіани та описати процедуру її визначення для
неперервних випадкових величин.
9. Дати означення математичногоочікування та вказати його
властивості.
10. Дати означення дисперсії та вказати її основні властивості.
11. Що таке моменти випадкових величин?
58

59.

Тема наступної лекції: «Системи випадкових величин та їх числові
характеристики. Найбільш поширені закони розподілу випадкових
величин»

60.

Лекцію завершено, дякую за увагу!