Л4 (Ч1-Ч2)_ТЙКС(13.11.25)

1.

1

2.

КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
імені ТАРАСА ШЕВЧЕНКА
Кафедра інформаційних систем та технологій
ТЕОРІЯ ЙМОВІРНОСТЕЙ та КОМП'ЮТЕРНА СТАТИСТИКА
Викладачі: Володимир ДРУЖИНІН; Ганна ТЕРЕЩУК
2025

3.

ЛЕКЦІЯ № 4. Частина 1,2: «Системи випадкових величин та їх числові
характеристики. Найбільш поширені закони розподілу випадкових величин»
ЧАСТИНА 1: «Системи випадкових величин та їх числові характеристики»
Навчальні питання:
1. Системи випадкових величин
2. Числові характеристики системи випадкових величин
3. Регресія однієї випадкової величини на іншу
4. Поняття про функції випадкових величин
2

4.

1. Системи випадкових величин
*** На практиці приходиться мати справу з випробуваннями, що несуть вплив
кількох випадкових явищ, кількох випадкових величин на кінцевий результат.
!!! Так, при стрільбі з гармати ми спостерігаємо відхилення від цілі як по відстані,
так і по напрямку.
Дві випадкові величини – відхилення по відстані і відхилення по напрямку –
утворюють систему.
Кілька випадкових величин, що впливають на результати випробування,
називаються системою і позначаються (X, Y,...,W), де дужки показують, що
розглядаються не окремі випадкові величини, а їх система.
3

5.

!!! Наочним є геометричне представлення системи випадкових величин.
Якщо розглядається система двох випадкових величин (X, Y), то результат
випробування можна представити як точку з координатами (хі, yі), система трьох
величин (X, Y, Z) визначає точку (xі, yі, zі) в тривимірному просторі.
*** Якість плавки чавуну є точкою в 120-вимірному просторі випадкових величин.
!!! Для завдання системи випадкових величин використовується закон
розподілу.
Законом розподілу системи називається співвідношення, яке встановлює
взаємозв’язок між областями можливих значень системи випадкових величин і
ймовірностями появи системи в цих областях.
4

6.

Закон розподілу системи може бути заданим в різних формах, зокрема у
вигляді таблиці розподілу, функції розподілу системи або щільності розподілу
системи.
5

7.

Таблиця розподілу системи випадкових величин (X, Y, Z,...,W) – це таблиця,
в якій вказані всі можливі комбінації значень величин, що входять до складу
системи, і ймовірності того, що випадкові величини приймуть одночасно
значення (xі, yj, zk ...,wl).
*** Загальний вигляд таблиці розподілу для системи двох випадкових величин
наведений на рис. нижче.
Рис. Таблиця розподілу системи двох величин
6

8.

При цьому
*** Властивості таблиці розподілу системи аналогічні властивостям ряду
розподілу одновимірної випадкової величини, зокрема, має місце рівність
(2.24)
!!! Враховуючи, що подія X=xi може з’явитися лише разом з однією з подій
Y=y1, Y=y2 , ..., Y=yn, за формулою повної ймовірності маємо
(2.25)
7

9.

З аналогічних міркувань
(2.26)
Функцією розподілу системи n випадкових величин називається функція
F(x, y,... ) n змінних, яка дорівнює ймовірності того, що випадкові величини X,
Y,... одночасно будуть задовольняти нерівностям X < x, Y < y,...
(2.27)
8

10.

ВЛАСТИВОСТІ функції F(x, y ,... )
1. Функція розподілу системи невід’ємна, не більше одиниці.
При прямуванні принаймні одного з аргументів до мінус нескінченності
функція прямує до нуля, при прямуванні всіх аргументів одночасно до плюс
нескінченності функція прямує до одиниці.
2. Функція розподілу системи – неспадна функція по кожному аргументу.
3. Якщо випадкова величина Х має функцію розподілу F(x), а випадкова
величина Y має функцію розподілу F(y), то
(2.28)
9

11.

4. Ймовірність влучення точки системи двох величин (X, Y) до довільного
прямокутника зі сторонами, паралельними координатним осям (рис.нижче),
обчислюється за формулою
(2.29)
10

12.

Функція розподілу, як і в випадку одновимірної випадкової величини,
придатна для характеристики систем як дискретних, так і неперервних
випадкових величин.
!!! Щільність розподілу системи випадкових величини визначається за
аналогією зі щільністю розподілу одновимірної випадкової величини.
Щільністю розподілу системи неперервних випадкових величин будемо
називати границю відношення ймовірності попадання випадкової точки в деяку
область до розмірів цієї області, коли розміри цієї області по кожній координаті
прямують до нуля.
11

13.

Для системи двох випадкових величин
12

14.

!!! Таким чином, щільність розподілу системи двох випадкових величин
дорівнює другій мішаній частинній похідній від функції розподілу системи
(2.31)
Властивості щільності розподілу системи неперервних випадкових величин:
1. Щільність розподілу невід’ємна.
2. Ймовірність того, що система випадкових величин прийме значення, що
буде належати області D, дорівнює визначеному інтегралу по області D від
щільності розподілу
(2.32)
13

15.

!!! Для одномірної випадкової величини графік щільності розподілу являв
плоску криву, а ймовірність того, що випадкова величина належала інтервалу
(а, b), дорівнювала площі криволінійної трапеції.
!!! Для системи двох випадкових величин щільність розподілу є деякою
поверхнею, і ймовірність того, що випадкова точка потрапить у межі області D,
дорівнює об’єму циліндричного тіла, обмеженого площиною x0y і поверхнею
f(x,y) щільності розподілу.
14

16.

Також за аналогією з раніше вивченими властивостями щільності
одновимірної величини для системи двох випадкових величин слушні
співвідношення
15

17.

Випадкові величини, що входять до системи, називаються незалежними,
якщо закон розподілу однієї з них не залежить від того, яких значень набули інші
величини, що входять до системи.
Для дискретних випадкових величин таблиця розподілу містить величини
pij=P(X=xi∩Y=yj),
*** тобто ймовірності сумісної появи двох подій
X=xi та Y=yj.
Для незалежних подій ймовірність їхньої сумісної появи – ймовірність
добутку – дорівнює добутку їх ймовірностей
(2.36)

18.

Для неперервної випадкової величини ймовірність
елементарної площадки (елемент ймовірності) дорівнює
появи
в
межах
f(x,y)·Δx·Δy.
Подія – влучення випадкової точки в межі прямокутника
(x<X<x+Δx, y<Y<y+Δy) – для незалежних подій
дорівнює добутку двох подій, ймовірність кожної з який дорівнює
відповідним елементам ймовірності
Р(х<X<x+Δx)=f(x)·Δx і P(y<Y<y+Δy)=f(y)·Δy,
де f(x) і f(y) – щільності розподілу випадкових величин X і Y відповідно.

19.

!!!Таким чином
Для дискретних незалежних випадкових величин ймовірність сумісної
появи будь-яких можливих значень дорівнює добутку відповідних ймовірностей.
Для неперервних незалежних випадкових величин щільність їхнього
сумісного розподілу дорівнює добутку щільностей розподілів кожної з величин.
18

20.

2. Числові характеристики системи випадкових величин
Система випадкових величин, як і одновимірна випадкова величина,
розглянута нами раніше, має свої числові характеристики.
!!! Зручно визначити ці числові характеристики через моменти системи
випадкових величин.
Початковим моментом порядку k+s системи двох випадкових величин (X, Y)
називається математичне очікування добутку Х встепені k наY в степені s
(2.38)
19

21.

УВАГА !!! Таким чином,
α01 і α10 – початкові моменти першого порядку,
α50, α41, ..., α14, α05 – початкові моменти п’ятого порядку.
20

22.

21

23.

Центральним моментом порядку k+s системи двох випадкових величин
(X, Y) називається математичне очікування добутку k-го і s-го степенів
відповідних центрованих величин.
*** Враховуючи, що центрована величина – це різниця між власне
випадковою величиною та її математичним очікуванням, маємо
(2.42)
де а=М(Х), b=M(Y).
22

24.

Обчислення виконують за формулами:
23

25.

!!! Центральні моменти другого порядку
μ20, μ02
є дисперсіями відповідних випадкових величин, що входять до системи.
*** Слід відмітити, що для системи (X,Y,Z,U) момент μ0020 = D(Z),
момент μ0002 = D(U) і т.д.
24

26.

Центральний момент другого порядку
μ11
називається кореляційним моментом (або другим мішаним моментом)
(2.45)
Оскільки для незалежних величин математичне очікування добутку дорівнює
добутку математичних очікувань, то
!!! тобто, для системи двох незалежних випадкових величин кореляційний
момент завжди дорівнює 0.
Зворотна властивість несправедлива, тобто, рівність нулю кореляційного
моменту ще не свідчить про незалежність випадкових величин, що входять до
системи.
25

27.

3. Регресія однієї випадкової величини на іншу
Нехай нам задана система двох дискретних випадкових величин (X, Y), тобто
перераховані всі можливі значення випадкових величин хі і уj і задані ймовірності
pij=P(X=xi∩Y=yj).
Події X=xi і Y=yj повинні наступити сумісно, тобто pij є ймовірністю добутку
двох подій.
В загальному випадку, якщо X і Y залежні, то за теоремою добутку
ймовірностей можна записати
26

28.

!!! Аналогічно можна одержати і таку формулу
*** Вирази
визначають умовні закони розподілу випадкових величин Y і X, тобто,
розподіли однієї випадкової величини, знайдені за умови, що інша випадкова
величина прийняла визначене значення.
З наведених вище формул витікає, що
(2.46)
27

29.

*** Цікаво відзначити, що
оскільки знаменники формул (2.46) менші 1.
Для системи неперервних випадкових величин введені поняття щільності
умовного розподілу, які за аналогією з системою дискретних величин
записуються у вигляді:
(2.47)
(2.48)
28

30.

!!! Умовний розподіл має свої числові характеристики – умовне математичне
очікування, умовну моду і так далі
Умовним математичним очікування
фіксованому значенні Y називається:
випадкової
величини
Х
при
- для системи дискретних випадкових величин – сума добутків можливих
значень Х на їхні умовні ймовірності
(2.49)
30

31.

- для системи неперервних випадкових величин – інтеграл від добутку
змінної на щільність умовного розподілу
(2.50)
УВАГА!!! На відміну від математичних очікувань М(Х) і М(Y), які є сталими
величинами, умовні математичні очікування МY(X), МХ(Y) залежать від того, які
значення прийняла інша випадкова величина, що входить до складу системи.
!!! Функція залежності умовного математичного очікування однієї
випадкової величини від значень іншої випадкової величини називається
регресією першої випадкової величини на іншу:

32.

*** Графіки функцій регресії називають лініями регресії.
Обчислимо математичне очікування випадкової величини, що входить до
складу системи матиме вигляд
!!! Отже, МО випадкової величини, що входить у систему, дорівнює МО
функції регресії.
32

33.

*** Для того, щоб знайти рівняння лінії регресії для заданої системи
випадкових величин, необхідно задатися видом функції регресії.
Припустимо, що лінії регресії є прямими лініями (найпростіший випадок).
Нагадаємо введені раніше позначення
Будемо шукати лінії регресії у вигляді прямої лінії, рівняння якої має вид
φ(х)=А(х–а)+В,
де А и В – невідомі нам константи.
33

34.

Відшукаємо математичне очікування регресії
Для того, щоб відшукати сталу А, визначимо мішаний (кореляційний)
момент
Таким чином
і рівняння прямої регресії має вид
(2.51)
34

35.

*** Аналогічно можна одержати рівняння прямої регресії ψ(у)
(2.52)
!!! Можна впевнитись, що обидві прямі проходять через центр розподілу,
тобто точку з координатами (а, b).
На практиці часто використовують коефіцієнт кореляції, який вводять за
формулою
(2.53)
35

36.

!!! Тоді рівняння регресії приймуть вид
(2.54)
Властивості коефіцієнта кореляції і прямих регресії.
1. Для незалежних випадкових величин коефіцієнт кореляції ρху = 0 і прямі
регресії φ(х)= b i ψ(у)= a паралельні координатним осям.
Рис. Еліпси розсіяння незалежних величин ( ρxy = 0)
36

37.

2. Якщо випадкові величини пов’язані лінійною функціональною залежністю,
то коефіцієнт кореляції за модулем дорівнює одиниці, а прямі регресії
співпадають.
3. В загальному випадку коефіцієнт кореляції за модулем не перевищує 1,
тобто,
!!! Якщо коефіцієнт кореляції відмінний від нуля, то випадкові величини
називаються корельованими (кореляційно залежними).
37

38.

*** На практиці вважається, що при
має місце сильна кореляційна залежність,
а при
слабка кореляційна залежність.
!!! Гострий кут між прямими регресії збільшується при зменшенні ρxy
Еліпси розсіяння кореляційно залежних величин
38

39.

4. Поняття про функції випадкових величин
*** Часто над випадковими величинами виконуються алгебраїчні дії, що
зумовлює необхідність розгляду результату цих дій як функції вихідних
випадкових величин.
Наприклад. Необхідно визначити закон розподілу випадкової величини Q
(прибуток підприємства), яка визначається за формулою
Q=С·Х ,
де величини С (вартість одиниці продукції) і Х (обсяги реалізації) є
випадковими величинами з деякими законами розподілу.
39

40.

УВАГА! ВИЗНАЧЕННЯ функції випадкової величини
Якщо кожному можливому значенню випадкової величини Х
відповідає одне можливе значення величини Y, то Y називають функцією
випадкового аргументу Х, тобто
Y= φ(Х).
Якщо кожній парі можливих значень випадкових величин Х і Y
відповідає одне можливе значення величини Z, то Z називають функцією
двох випадкових аргументів Х і Y, тобто
Z= ψ(Х,Y).
40

41.

ПРИКЛАД. Дискретна випадкова величина Х задана рядом розподілу
ЗАВДАННЯ. Скласти ряд розподілу випадкової величини
Функція дискретного випадкового аргументу є також дискретною
випадковою величиною, можливі значення якої визначаються як значення тієї ж
функції для конкретних значень аргументу ( в данному випадку
41

42.

Ймовірність кожного значення уі дорівнює ймовірності відповідного
значення хі, тобто рі.
!!! Якщо різним значенням аргументу хі відповідають однакові
значення функції уі, значення уі в ряд розподілу величини Y заноситься
один раз, а відповідна йому ймовірність визначається як сума
ймовірностей всіх значень хі, які відповідають одному й тому ж
значенню функції Y.
42

43.

Остаточно ряд розподілу випадкової величини Y набуває виду
!!! У випадку, коли аргумент функції
Y=φ(Х)
є неперервною випадковою величиною, сама функція може бути як неперервною,
так і дискретною випадковою величиною.
*** Якщо функція у=φ(х), визначена на множині значень неперервної
випадкової величини Х, є неперервною функцією без інтервалів сталості, то
випадкова величина Y буде також неперервною.
!!! В таких випадках зазвичай ставиться задача визначення щільності
43
розподілу величини Y по відомій щільності розподілу величини Х.

44.

ПРИКЛАД. Нехай на інтервалі можливих значень х функція
у=φ(х)
є монотонно зростаючою функцією, для якої визначена перша похідна.
Тоді, як видно з рис. вище, довільний внутрішній інтервал (х1, х2)
відображається функцією φ(х) на інтервал (у1, у2), отже,
Р(х1 < X < x2) = P(y1 < Y < y2).
Якщо закон розподілу Х задано щільністю розподілу f(x), то
44

45.

!!! З урахуванням виду функції φ(х) зробимо заміну змінної інтегрування,
для чого виразимо х через у:
де ψ(у) – функція, обернена до φ(х).
*** Враховуючи, що
dx = ψ ’ (y) dy,
отримуємо
45

46.

!!! При обчисленні ймовірностей неперервних величин підінтегральна
функція має зміст щільності розподілу, тому вираз
f(ψ(y))·ψ′(y)=g(y)
слід розглядати як щільність розподілу неперервної випадкової величини Y.
*** Отже
g(y)= f(ψ(y))·ψ′(y),
або
g(y)·dy = f(x)·dx.
Таким чином, для функції неперервних випадкових величин має місце
рівність елементів ймовірностей.
46

47.

!!! В іншому випадку (рис. вище), коли функція
у=φ(х)
є спадною, рівність слід записати в такому вигляді
Після зміни напрямку інтегрування отримаємо
де ψ′(y) < 0 як похідна від спадної функції.
!!! Об’єднуючи два випадки, можна остаточно записати
47

48.

ЧАСТИНА 2: «Найбільш поширені закони розподілу випадкових величин»
Питання:
1. Найпростіші закони розподілу дискретних випадкових величин
2. Біномний розподіл
3. Розподіл Пуассона
4. Геометричний розподіл
5. Розподіл Паскаля
6. Гіпергеометричний розподіл
7. Показниковий розподіл
8. Рівномірний розподіл неперервної величини
9. Нормальний розподіл
48

49.

1. Найпростіші закони розподілу дискретних випадкових величин
До найпростіших законів розподілу дискретних випадкових величин можна
віднести рівномірний розподіл і розподіл Бернуллі.
!!! Дискретна величина Х має рівномірний розподіл, якщо кожне з її n
можливих значень має однакову ймовірність.
ПРИКЛАД. Кількість очок при киданні грального кубика, коли ряд
розподілу має вид
49

50.

Числові характеристики рівномірно розподіленої дискретної випадкової
величини Х визначимо, виходячи з того, що в загальному випадку значення xi
змінюються на інтервалі
[a, b]
з кроком
h,
тобто,
х1 = а, х2 = а+h, x3 = a+2h,..., xn = a+(n–1)·h = b.
Ймовірність кожного такого значення
pi=1/n ,
отже, МО дорівнює

51.

Для визначення дисперсії відшукаємо
!!! Тоді
51

52.

НАПРИКЛАД, для кидання грального кубика, коли а=1, b = 6, n = 6, h=1,
маємо
M(X)=3,5; D(X) =2,917
!!! Дискретний рівномірний розподіл симетричний, отже, медіана
дорівнює математичному очікуванню.
!!! Мода розподілу не визначена.
52

53.

Розподілу Бернуллі
Нехай в досить великій за об’ємом сукупності частина об’єктів має задану
властивість.
Якщо з сукупності вилучити один об’єкт, то ймовірність появи об’єкту з
заданою властивістю дорівнює р, де р – доля таких об’єктів у сукупності.
*** Позначимо
хі = 1
якщо в і-му досліді з’явилась подія А і
хі = 0
в іншому випадку.
Тоді ряд розподілу випадкової величини Х має вид (розподіл Бернуллі)
53

54.

Для розподілу Бернуллі математичне очікування, дисперсія і коефіцієнт
асиметрії дорівнюють
!!! Розподіл Бернуллі є відправним при аналізі багатьох інших, більш
складних, розподілів.
54

55.

2. Біномний розподіл
ПРИКЛАД. Розглянемо випадкову величину Х – кількість появ деякої події
А в серії з n повторних випробувань за схемою Бернуллі (ймовірність появи події
в кожному випробуванні є сталою і дорівнює р).
*** Зрозуміло, що можливими значеннями величини Х є
х1= 0, х2 = 1, х3=2,..., хn+1= n.
Ймовірність прийняття величиною Х певного значення k визначається за
формулою Бернуллі
55

56.

Формула (3.6) і задає біномний розподіл дискретної випадкової величини Х.
Розподіл називається біномним (або біноміальним) тому, що ймовірність
кожного значення випадкової величини Х=k відповідно до формули (3.6) є k-тим
членом розвинення в ряд біному Ньютона
Твірна функція
має таку властивість: числовий коефіцієнт перед х в степені k дорівнює
імовірності того, що в n випробуваннях подія відбудеться рівно k разів.
56

57.

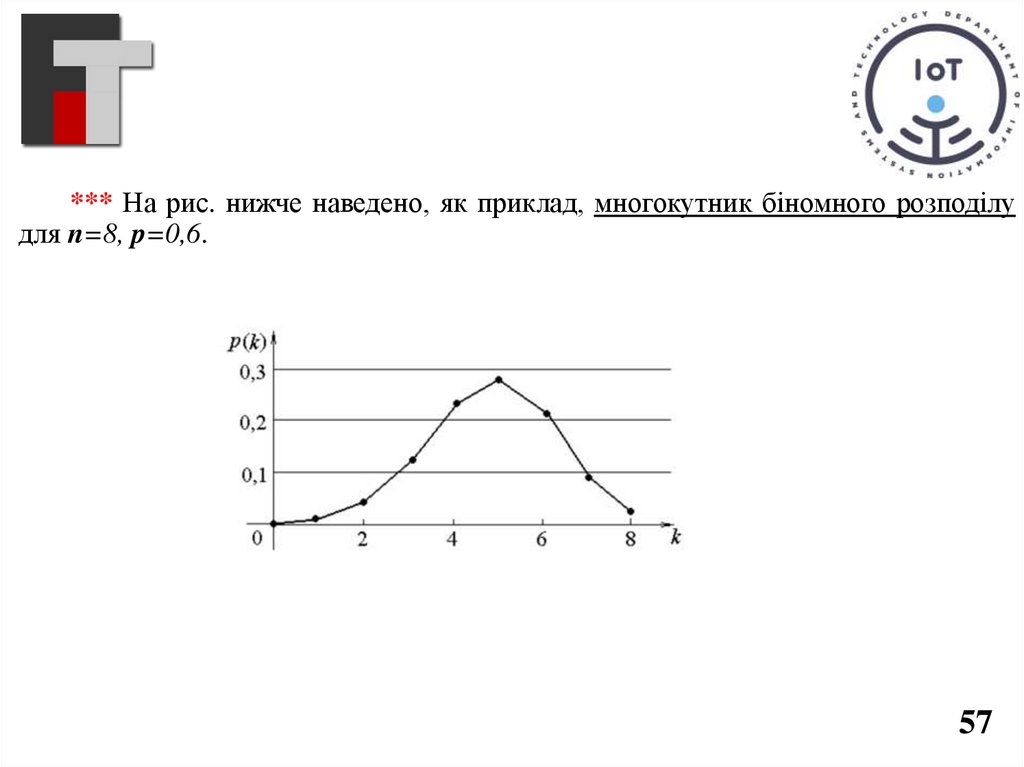
*** На рис. нижче наведено, як приклад, многокутник біномного розподілу
для n=8, p=0,6.
57

58.

Числові характеристики розподілу легко отримати, якщо представити
випадкову величину Х=k як суму n значень розподілу Бернуллі.
Тоді маємо
Мода біномного розподілу (k0) називається також найімовірнішим числом
появи подій і обчислюється із співвідношення
58

59.

*** Далі, підставляючи в кожну з нерівностей наведених вище відповідні
вирази формули Бернуллі і скорочуючи на невід’ємні степені і факторіали,
отримуємо
*** Оскільки всі можливі значення величини Х є цілими числами, то і модою
біномного розподілу є ціле число з визначеного вище інтервалу.
!!! Зауважимо, що можлива ситуація, коли два цілих числа задовольняють
співвідношенням (3.8). Тому на практиці застосовують таку схему визначення
моди біномного розподілу.
!!! Якщо величина p∙(п+1) є дробовим числом, то мода Мо дорівнює цілій
частині цього числа. Якщо ж величина p∙(п+1) є цілим числом, то існує два
значення моди:
59

60.

3. Розподіл Пуассона
Розподіл Пуассона є граничним випадком біномного розподілу, коли
ймовірність появи події при одному випробуванні досить мала, а число
випробувань велике.
*** Його називають також законом рідких подій і задають формулою
Пуассона.
Для розподілу Пуассона
60

61.

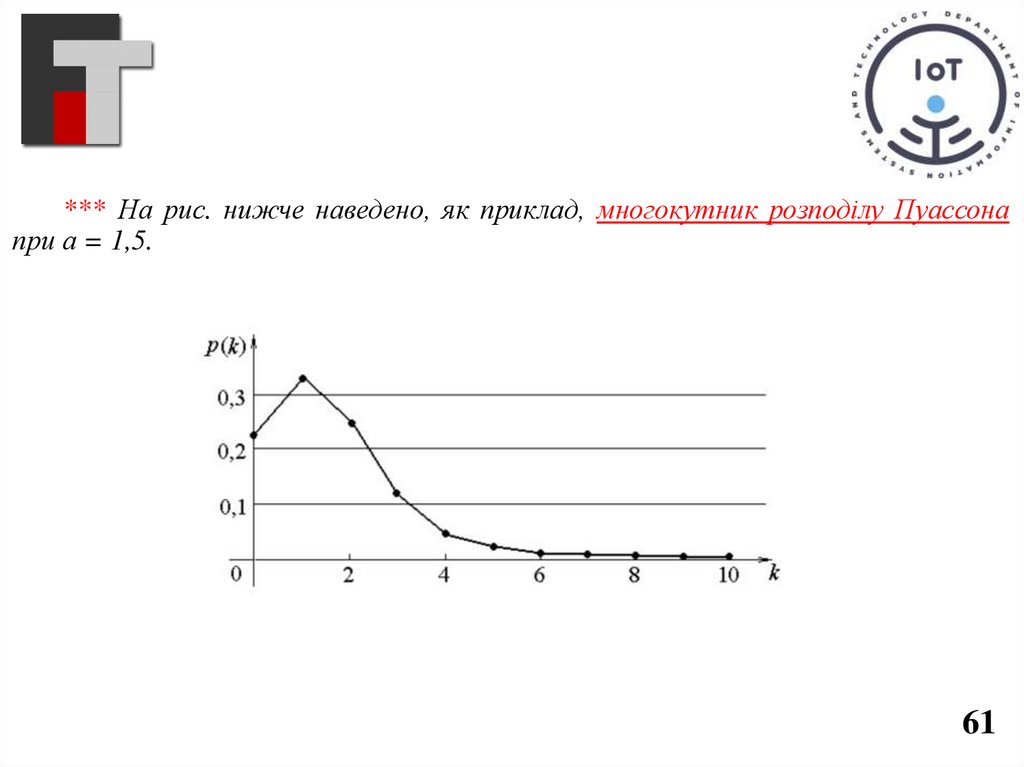
*** На рис. нижче наведено, як приклад, многокутник розподілу Пуассона
при а = 1,5.
61

62.

!!! Слід зазначити, що розподіл Пуассона може розглядатись як модель появи
незалежних подій, що виникають послідовно у випадкові моменти часу.
*** Дійсно, якщо λ – інтенсивність появи подій (середня кількість подій за
одиницю часу), тоді
а = λ·t,
і ймовірність появи події k разів за час t обчислюється за формулою
Пуассона (3.9)
62

63.

ПРИКЛАД. При роботі комп’ютера трапляється в середньому одна відмова
протягом двох годин. Яка імовірність, що за одну годину не буде жодної
відмови?
Розв’язання. З умови задачі витікає, що λ = 0,5 (одна відмова за дві години),
t = 1, а = λ·t 0,5, k = 0 (жодної відмови).
Отже, за формулою (3.9) маємо
63

64.

Числові характеристики розподілу Пуассона.
64

65.

Отже,
Як видно, для розподілу Пуассона математичне очікування співпадає з
дисперсією.
!!! Ця властивість використовується на практиці. Якщо за результатами
випробувань одержано, що
М(Х) ≈ D(X),
то це свідчить на користь припущення про пуассонівський розподіл випадкової
65
величини X.

66.

Моду шукаємо як таке число k0, для якого справедливе співвідношення
Враховуючи формулу (3.9), маємо
З лівої нерівності маємо
66

67.

з правої –
!!! Таким чином
тобто, модою є ціле число з інтервалу
[а – 1, а].
67

68.

4. Геометричний розподіл
*** Нехай ймовірність появи події при одному випробуванні
P(A) = p,
ймовірність непояви
!!! Випробування відбуваються до першої появи події.
Позначимо X = k – кількість випробувань до першої появи події (тобто кількість
невдалих випробувань).
Очевидно, що X = 0 у випадку, коли вже в першому випробуванні подія з’явилася;
X = 1 у випадку, коли в першому випробуванні подія не з’явилася, а в другому –
з’явилася;
X = k у випадку, коли в k випробуваннях подія не з’явилася, а в (k+1)-му – з’явилася.

69.

Отже,
Ряд розподілу має вигляд:
69

70.

Елементи розподілу ймовірностей мають вигляд членів геометричної
прогресії з першим членом p і знаменником q.
Тому розподіл називають геометричним. Сума всіх ймовірностей
*** Для визначення M(X) і дисперсії D(X) виведемо деякі допоміжні формули
шляхом тотожних перетворень виразу для суми геометричної прогресії
70

71.

Перш за все, візьмемо похідну по q від правої і лівої частин:
Праву і ліву частини одержаної формули помножимо на q
та ще раз відшукаємо похідну:
71

72.

Враховуючи формули (3.13)–(3.14), маємо
73

73.

74

74.

5. Розподіл Паскаля
*** Позначимо
Випробування повторюються до тих пір, поки подія А не з’явиться r разів,
r > 0.
Випадкова величина k – кількість невдалих випробувань до появи події r
разів, включаючи і останнє випробування.
*** Розглянемо дві незалежні події:
V: в (r+k–1) випробуваннях подія А відбулась рівно (r–1) раз;
W: в (r+k)-му випробуванні подія відбулась r-й раз.
!!! Очевидно, що подія X = k матиме місце в результаті сумісної появи подій
V і W.
75

75.

Отже,
!!! Розподіл, що описується формулою (3.16), називається розподілом
Паскаля.
*** Розглядаючи розподіл Паскаля як суму r геометричних розподілів,
отримаємо його числові характеристики:
76

76.

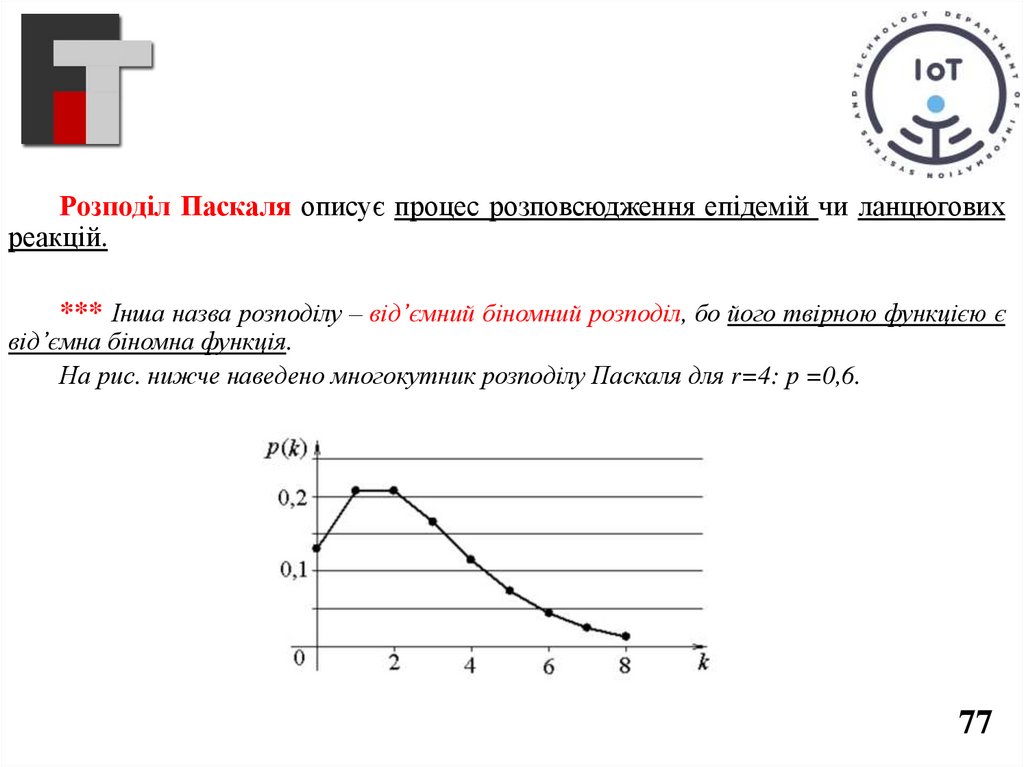
Розподіл Паскаля описує процес розповсюдження епідемій чи ланцюгових
реакцій.
*** Інша назва розподілу – від’ємний біномний розподіл, бо його твірною функцією є
від’ємна біномна функція.
На рис. нижче наведено многокутник розподілу Паскаля для r=4: р =0,6.
77

77.

6. Гіпергеометричний розподіл
*** В усіх розглянутих раніше випадках моделлю була послідовність
незалежних випробувань, коли ймовірність появи події А в одному випробуванні
залишається сталою.
!!! Таке припущення не завжди є слушним.
Розглянемо таку модель. Нехай партія містить N виробів, з них n виробів мають
задану властивість,
0 < n < N.
Наздогад узято m виробів,
0 < m < N.
Випадкова величина Х = k, де k – кількість виробів з заданою властивістю серед
узятих,
max(0, m+n–N) ≤ k ≤ min(n, m).
78

78.

79

79.

Розподіл, що описується формулою (3.18), називається гіпергеометричним
розподілом.
*** Цей розподіл використовується в практиці статистичного контролю якості
продукції і в різних задачах, пов’язаних з організацією вибіркових досліджень.
!!! В розглянутій моделі дослідів випробування є залежними.
Доведено, що числові характеристики розподілу приймають такі значення
80

80.

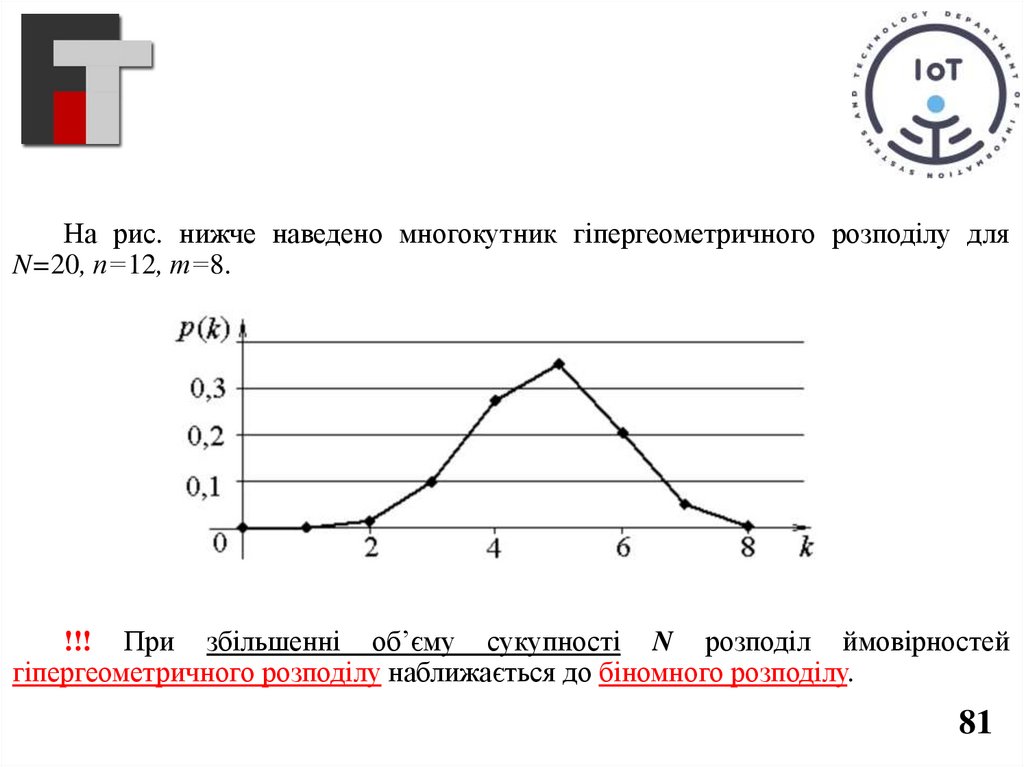
На рис. нижче наведено многокутник гіпергеометричного розподілу для
N=20, п=12, т=8.
!!! При збільшенні об’єму сукупності N розподіл ймовірностей
гіпергеометричного розподілу наближається до біномного розподілу.
81

81.

7. Показниковий розподіл
*** В контексті розгляду даного питання проаналізуємо послідовність випадкових
подій в часі.
Якщо розподіл Пуассона дозволяв обчислювати ймовірність появи подій кілька разів
протягом фіксованого часового інтервалу, то тепер розглянемо іншу випадкову величину
– час між двома подіями в цій послідовності.
!!! Зрозуміло, що ця величина є неперервною.
Знайдемо ймовірність того, що випадкова величина Т прийме значення,
більше від поточного значення t, тобто за час t подія не з’явилась жодного разу:
82

82.

!!! Тепер перейдемо до протилежної події:
УВАГА! Остання ймовірність (див. вище) за означенням дорівнює
інтегральній функції розподілу випадкової величини Т.
Отже,
Розподіл, що описується функцією розподілу (3.20) або щільністю розподілу
(3.21), називається показниковим розподілом. Типові графіки вказаних функцій
показані на рис. вище
83

83.

Отримаємо вирази для числових характеристик показникового закону
розподілу.
84

84.

!!! Таким чином, числові характеристики випадкової величини, розподіленої
за показниковим законом, мають значення
Ймовірність того, що випадкова величина, розподілена за показниковим
законом, попаде на інтервал (a; b), обчислимо за властивістю функції розподілу
85

85.

Основною областю застосування показникового розподілу є розрахунки середнього
часу безвідмовної роботи складних технічних систем.
При великій кількості елементів, з яких складається пристрій, кожен з елементів
може вийти з ладу у довільний момент часу, тому надійність складних систем
змінюється з часом за показниковим законом.
!!! Для аналізу надійності складних систем вводиться поняття середнього
часу безвідмовної роботи системи
та функції надійності
яка задає закон зміни надійності в часі.
86

86.

!!! Вважаючи, що випадкова величина Т (час безвідмовної роботи системи)
розподілена за показниковим законом, маємо
*** Розглянемо послідовне і паралельне з’єднання блоків складної системи,
середній час безвідмовної роботи кожного з яких дорівнює
!!! У випадку послідовного з’єднання безвідмовна робота системи
забезпечується безвідмовною роботою кожного блоку . Отже, маємо:
87

87.

Таким чином, при послідовному з’єднанні блоків функція надійності всієї
системи має показниковий закон розподілу, і середній час безвідмовної роботи
системи знаходиться за формулою:
При паралельному з’єднанні, коли для безвідмовної роботи пристрою
достатньо працездатності одного з дублюючих блоків, закон зміни функції
надійності пристрою в цілому відрізняється від показникового.
88

88.

Середній час безвідмовної роботи обчислюється за формулами:
89

89.

8. Рівномірний розподіл неперервної величини
Неперервна випадкова величина розподілена за рівномірним законом на
інтервалі [a, b], якщо щільність розподілу на цьому інтервалі є сталою:
Після визначення сталої С з умови
маємо
90

90.

Інтегральна функція розподілу шукається за формулою
Після виконання інтегрування одержимо
Ймовірність попадання рівномірно розподіленої величини на інтервал
обчислюється за формулою

91.

!!! Рівномірний розподіл використовується, коли неперервна випадкова
величина з однаковою ймовірністю може прийняти будь-яке значення на
обмеженому інтервалі.
Числові характеристики
стандартними формулами
рівномірного
розподілу
шукаються
за

92.

Розподіл симетричний, плосковершинний, отже
М(Х) = Ме,
коефіцієнт асиметрії
Сs = 0,
!!! Мода рівномірного розподілу не визначена.
!!! Слід звернути увагу на те, що результати аналізу випадкових величин
суттєво залежать від вибору моделі розподілу величини.
93

93.

9. Нормальний розподіл
Випадкова величина Х вважається розподіленою за нормальним розподілом
(або розподілом Гаусса), якщо щільність розподілу її ймовірностей описується
функцією
*** Інтегральна
виражається.
функція
розподілу
через
елементарні
функції
не
!!! Крива щільності розподілу одномодальна і симетрична, тому центр
розподілу легко знайти з умови
94

94.

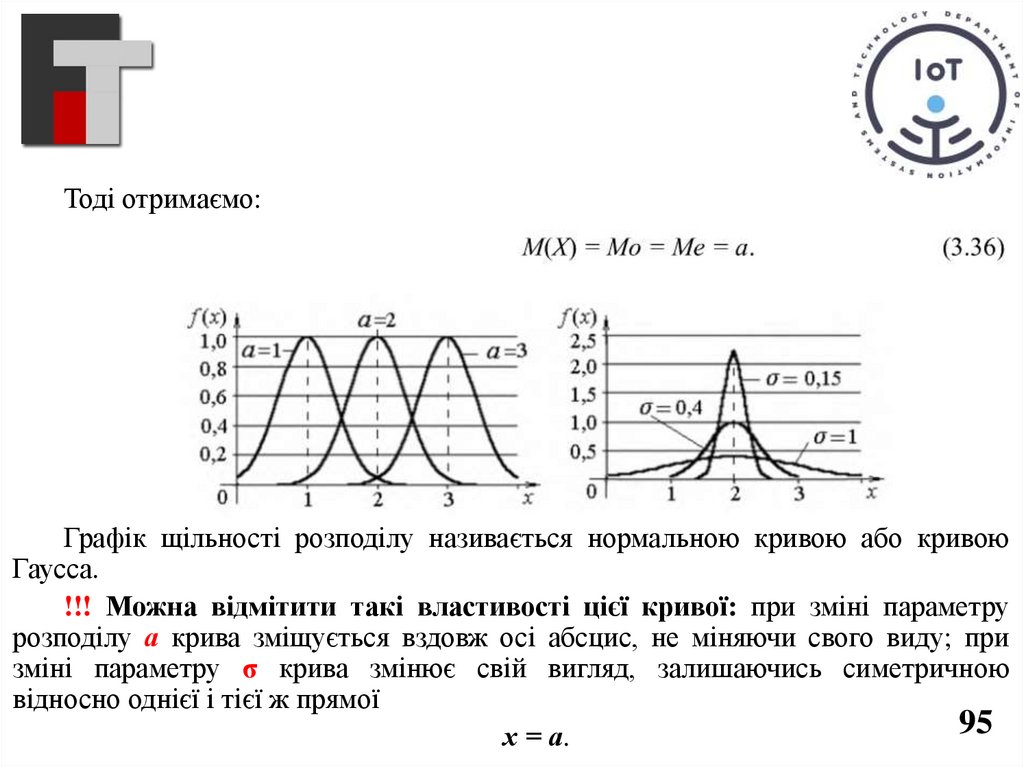
Тоді отримаємо:
Графік щільності розподілу називається нормальною кривою або кривою
Гаусса.
!!! Можна відмітити такі властивості цієї кривої: при зміні параметру
розподілу а крива зміщується вздовж осі абсцис, не міняючи свого виду; при
зміні параметру σ крива змінює свій вигляд, залишаючись симетричною
відносно однієї і тієї ж прямої
95
х = а.

95.

Ймовірність того, що випадкова величина, розподілена за нормальним
законом з відомими числовими характеристиками М(Х) і D(X), попаде на
інтервал (α, β) розраховується за формулою:
96

96.

*** Якщо позначити
як інтеграл ймовірностей (функція Лапласа)
Тоді
!!! Для функції Лапласа складені таблиці , при їх використанні треба враховувати,
що функція непарна, тобто Ф(–и) = – Ф(и).
До того ж в різних довідниках наведені різні модифікації функції Лапласа, тому
перед користуванням таблицями слід детально ознайомитись з їх описом.
97

97.

*** Правило 3ϭ
Приблизно з ймовірністю 0,9973 значення
випадкової величини X лежить у інтервалі
нормально
розподіленої
а-3σ ≤ X ≤ а+3σ,
де
а,σ - параметри розподілу випадкової величини X .
98

98.

!!! Результати досліджень, виконаних в середині ХІХ століття,
продемонстрували широке розповсюдження нормального розподілу в біології,
техніці і інших галузях знання.
Пояснення цьому факту дає центральна гранична теорема, яка була
сформульована П. Л. Чебишевим і доведена О. М. Ляпуновим.
Не розглядаючи детально саму теорему і її доведення, зауважимо лише, що
для практичного застосування важливим є наслідок з теореми, який звучить так:
якщо випадкова величина Х є сумою великої кількості випадкових величин, вплив
кожної з яких на суму незначний, то Х має розподіл, що наближається до
нормального розподілу.
99

99.

Контрольні питання
1. Що таке системи випадкових величин і які форми їх завдання?
2. Як визначається функція розподілу системи випадкових величин і які властивості
вона має?
3. Як визначається функція щільності розподілу системи випадкових величин і які
властивості вона має?
4. Що таке умовні закони розподілу ? Наведіть приклади.
5. Що таке регресія однієї випадкової величини на іншу?
6. Дати означення коефіцієнта кореляції. Які його властивості?
7. Описати процедуру побудови рівнянь регресії.
8. Дати означення функції випадкового аргументу.
9. Описати процедуру побудови ряду розподілу для функції дискретного випадкового
аргументу.
10. Описати процедуру знаходження щільності розподілу для функції неперервного
випадкового аргументу.
100

100.

Контрольні питання
11. Для кожного з перерахованих законів вказати модель, параметри, що визначають
закон, та основні числові характеристики.
11.1 . Дискретний рівномірний розподіл.
11.2 . Розподіл Бернуллі.
11.3 . Біномний розподіл.
11.4 . Геометричний розподіл.
11.5 . Розподіл Паскаля.
11.6 . Гіпергеометричний розподіл.
11.7 . Розподіл Пуассона.
11.8 . Показниковий розподіл.
11.9 . Рівномірний неперервний розподіл.
11.10. Нормальний розподіл.
12. Сформулювати правило “трьох сигм”. Пояснити, чим зумовлено широке
застосування нормального розподілу на практиці.
101

101.

Тема наступної лекції: «Закон великих чисел. Необхідна та достатня
умова для закону великих чисел. Посилений закон великих чисел. Центральна
гранична теорема»

102.

Лекцію завершено, дякую за увагу!