Доклад7

1.

Специальность: 2.3.1. «Системный анализ, управление и обработка информации, статистика»
КОМБИНАТОРНЫЙ ПОИСК В ЗАДАЧАХ БОЛЬШОЙ РАЗМЕРНОСТИ С
РАЗВИВАЮЩЕЙСЯ МОДЕЛЬЮ ПРЕДМЕТНОЙ ОБЛАСТИ
Докладчик:
Олейник Юрий Андреевич
– н.с. лаб. №21 ИИММ КНЦ РАН
Научный руководитель:
Зуенко Александр Анатольевич – к.т.н., в.н.с. лаб. №21 ИИММ КНЦ РАН

2.

Актуальность темы работы. При решении задач комбинаторного поиска, в которых требуется
поддерживать развивающуюся модель предметной области, зачастую, использование
существующих методов исследования операций затруднено в связи с их ориентацией на
эффективное решение конкретных подклассов задач, причем, добавление к задаче
дополнительных условий может привести к принципиальному изменению используемой
схемы ее решения. Ситуация еще более осложняется, когда необходимо анализировать
большие объемы входной информации.
В связи с этим, возникает потребность в новых методах, обеспечивающих приемлемое время
решения задач высокой размерности при поддержке возможности гибкого учета и анализа
новых условий задачи.
Целью диссертационной работы является разработка интеллектуальных подходов и
методов, обеспечивающих повышение размерности решаемых задач комбинаторного
поиска с развивающейся моделью предметной области.
2

3.

Задачи работы:
1. Анализ методов решения задач комбинаторного поиска, их систематизация и оценка
применимости к задачам большой размерности с развивающейся моделью предметной
области.
2. Разработка подхода к поэтапной модификации представления задач комбинаторного
поиска для поддержки развивающейся модели предметной области при решении задач
больших размерностей.
3. Разработка на основе предложенного подхода последовательности моделей
планирования открытых горных работ, где каждая последующая модель обеспечивает
увеличение размерности решаемой задачи при более компактном ее представлении.
4. Разработка оригинальных методов удовлетворения ограничений, использующих
усовершенствованную модель.
5. Программная реализация разработанных моделей. Оценка результатов работы
предложенных методов и алгоритмов.
3

4.

Научная новизна работы:
1. В рамках парадигмы программирования в ограничениях разработан подход к итеративной
модификации представления задач комбинаторного поиска, отличающийся возможностью
оперативно перестраивать методы поиска при увеличении размерности задачи и
введении в модель предметной области новых ограничений.
2. Впервые предложено моделировать класс задач планирования открытых горных работ в
виде сети ограничений с применением развитого механизма глобальных ограничений, что
позволяет унифицировано описывать и обрабатывать разнородные условия задачи.
3. Разработан гибридный метод поиска рационального решения задачи планирования
открытых горных работ, отличающийся применением оригинальных процедур
рассуждений на совокупностях однотипных ограничений, которые обеспечивают более
глубокую редукцию пространства поиска.
4

5.

Положения, выносимые на защиту:
1. Подход в рамках парадигмы программирования в ограничениях к поэтапной
модификации представления задач комбинаторного поиска большой размерности с
развивающейся моделью предметной области, в частности, задач планирования открытых
горных работ.
2. Модель класса задач планирования открытых горных работ в виде сети ограничений,
включающей глобальные ограничения, формализующие разнородные условия задачи.
3. Гибридный метод поиска рационального решения задачи планирования открытых горных
работ.
5

6.

Соответствие диссертации научной специальности
Результаты диссертационной работы соответствуют специальности 2.3.1 – «Системный анализ,
управление и обработка информации, статистика» пунктам:
1. Теоретические основы и методы системного анализа, оптимизации, управления, принятия решений,
обработки информации и искусственного интеллекта.
2. Формализация и постановка задач системного анализа, оптимизации, управления, принятия решений,
обработки информации и искусственного интеллекта.
4. Разработка методов и алгоритмов решения задач системного анализа, оптимизации, управления,
принятия решений, обработки информации и искусственного интеллекта.
5. Разработка специального математического и алгоритмического обеспечения систем анализа,
оптимизации, управления, принятия решений, обработки информации и искусственного интеллекта.
9. Разработка проблемно-ориентированных систем управления, принятия решений и оптимизации
технических объектов.
10. Методы и алгоритмы интеллектуальной поддержки при принятии управленческих решений в
технических системах.
6

7.

Комбинаторные задачи большой размерности возникают в ситуациях, когда
количество возможных решений настолько велико, что полный перебор всех
вариантов становится практически невозможным даже для современных
вычислительных мощностей. Такие задачи часто возникают в логистике,
экономике, проектировании сетей, анализе больших данных, горном
производстве и т.п.
Задача 1
Комбинаторные задачи большой размерности
с развивающейся моделью предметной области
Под развитием предметной области подразумевается возможность
оперативного добавления к условиям задачи новых условий или
закономерностей, дополняющих ее постановку.
С учетом этих особенностей к методологии решения таких задач предъявляются
следующие требования:
• компактность описания задачи в памяти компьютера;
• возможность использования разнородных зависимостей;
• поддержка оперативного расширения условий задачи новыми
ограничениями;
• возможность применять различные методы поиска решений в зависимости
7

8.

Точные методы:
Поиск с возвратами.
Смешанная целочисленная оптимизация.
Динамическое программирование.
Приближенные методы:
Генетические алгоритмы.
Алгоритмы роевого интеллекта.
Имитация отжига.
Плюсы:
• поиск всех решений;
• нахождение оптимального решения.
Минусы:
• трудность исследования больших пространств.
Задача 1
Методы дискретной оптимизации
Плюсы:
• слабая зависимость от размерности задачи.
Минусы:
• вероятность пропуска решений, отсутствие гарантии
нахождения оптимального решения;
• вероятность «застревания».
Гибридные методы:
Поиск в большой окрестности (Large
neighborhood search).
Объединяют достоинства точных и приближенных
методов.
8

9.

Задача 1
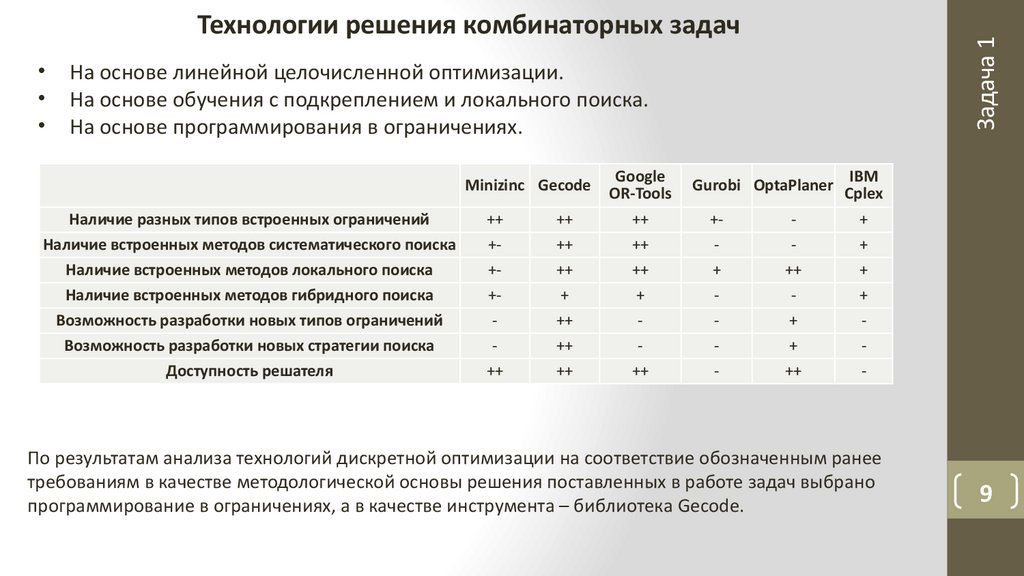
Технологии решения комбинаторных задач
На основе линейной целочисленной оптимизации.
На основе обучения с подкреплением и локального поиска.
На основе программирования в ограничениях.
Minizinc Gecode
Наличие разных типов встроенных ограничений
Наличие встроенных методов систематического поиска
Наличие встроенных методов локального поиска
Наличие встроенных методов гибридного поиска
Возможность разработки новых типов ограничений
Возможность разработки новых стратегии поиска
Доступность решателя
++
+++++
++
++
++
+
++
++
++
Google
OR-Tools
++
++
++
+
++
Gurobi OptaPlaner
++
-
++
+
+
++
IBM
Cplex
+
+
+
+
-
По результатам анализа технологий дискретной оптимизации на соответствие обозначенным ранее
требованиям в качестве методологической основы решения поставленных в работе задач выбрано
программирование в ограничениях, а в качестве инструмента – библиотека Gecode.
9

10.

…
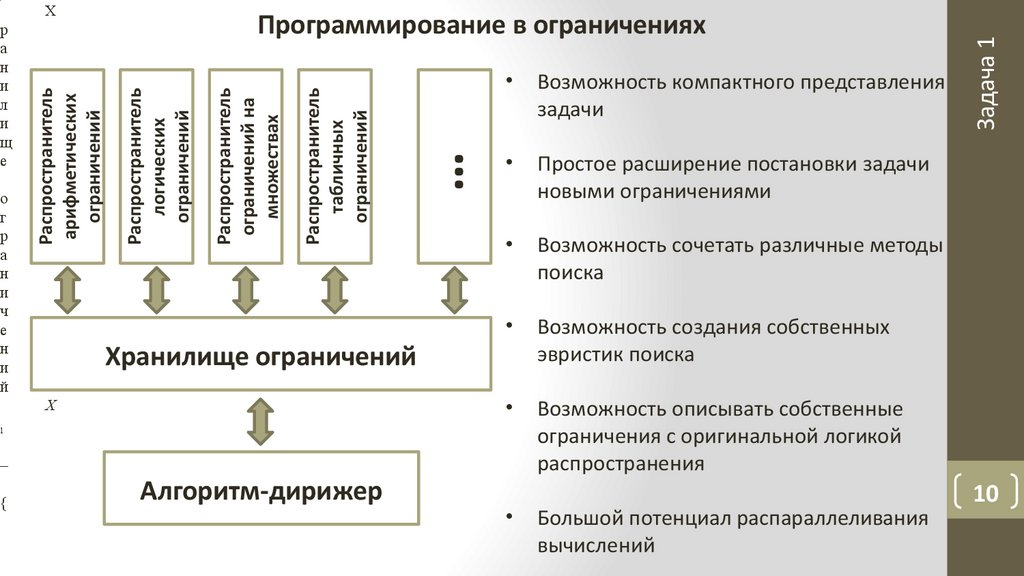
Возможность компактного представления
задачи
Простое расширение постановки задачи
новыми ограничениями
Возможность сочетать различные методы
поиска
Возможность создания собственных
эвристик поиска
Возможность описывать собственные
ограничения с оригинальной логикой
распространения
Хранилище ограничений
X
1
–
{
Алгоритм-дирижер
Большой потенциал распараллеливания
вычислений
Задача 1
Распространитель
табличных
ограничений
Распространитель
ограничений на
множествах
Программирование в ограничениях
Распространитель
логических
ограничений
о
г
р
а
н
и
ч
е
н
и
й
Распространитель
арифметических
ограничений
р
а
н
и
л
и
щ
е
Х
10

11.

Карьер — совокупность выемок в земной коре, образованных при добыче полезного
ископаемого открытым способом.
Планирование открытых горных работ – определение положений карьера на разных
этапах его разработки.
Задача 1
Открытые горные работы (класс задач Open pit mining)
11

12.

Методы
Линейное целочисленное
программирование
Динамическое программирование
Недостатки
Генетические алгоритмы
Задача 1
Существующие методы решения задачи планирования открытых
горных работ
сложность представления качественных
зависимостей;
большой размер представления задачи в памяти
ЭВМ;
низкая размерность решаемых задач.
сложность формирования начальной популяции
решений, особенно для задач большой
размерности;
слабая поддержка развивающейся модели
предметной области.
12

13.

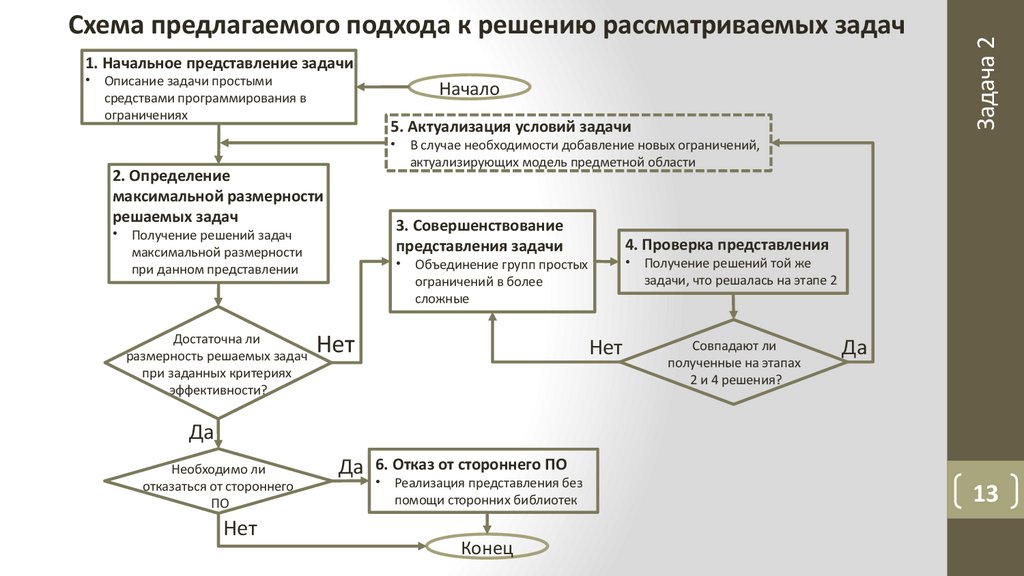
1. Начальное представление задачи
• Описание задачи простыми
средствами программирования в
ограничениях
Начало
5. Актуализация условий задачи
• В случае необходимости добавление новых ограничений,
актуализирующих модель предметной области
2. Определение
максимальной размерности
решаемых задач
3. Совершенствование
представления задачи
• Получение решений задач
максимальной размерности
при данном представлении
Достаточна ли
размерность решаемых задач
при заданных критериях
эффективности?
Задача 2
Схема предлагаемого подхода к решению рассматриваемых задач
4. Проверка представления
• Получение решений той же
задачи, что решалась на этапе 2
• Объединение групп простых
ограничений в более
сложные
Нет
Нет
Совпадают ли
полученные на этапах
2 и 4 решения?
Да
Да
Необходимо ли
отказаться от стороннего
ПО
Нет
Да 6. Отказ от стороннего ПО
• Реализация представления без
помощи сторонних библиотек
Конец
13

14.

Bwt – множество
вскрышных блоков,
извлекаемых в год t, т.е.
если bi ∈ Bt, то ti = t и Ci ≤ 0.
Задача 3
Постановка задачи планирования открытых горных работ
Bot – множество рудных
блоков, извлекаемых в год t,
т.е. если bi ∈ Bot, то ti = t и Ci > 0.
Решение задачи: назначение каждому
блоку номера периода добычи.
Экономические ограничения:
wmint ≤ |Вwt| ≤ wmaxt,
omint ≤ |Bot| ≤ omaxt.
Технологические ограничения:
B’i – блоки, которые необходимо извлечь не позже блока bi, т.е. если bk ∈ B’i, то tk ≤ ti.
(технологические ограничения)
Целевая функция: ∑F(Ci, ti) → max.
Размерность практически значимых задач: |B|>100000, T >10.
Шаблон добычи
14

15.

Задача 3
Представление в линейном целочисленном программировании
15

16.

Задача 3
Представление с простыми ограничениями
gcc – global cardinality constraint.
gcc(X, V, Y): среди переменных X ровно Yi
переменных должны принимать значение Vi.
16

17.

Задача 3
Представление с использованием ограничения «max»
17

18.

Задача 4
Усовершенствованное представление
18

19.

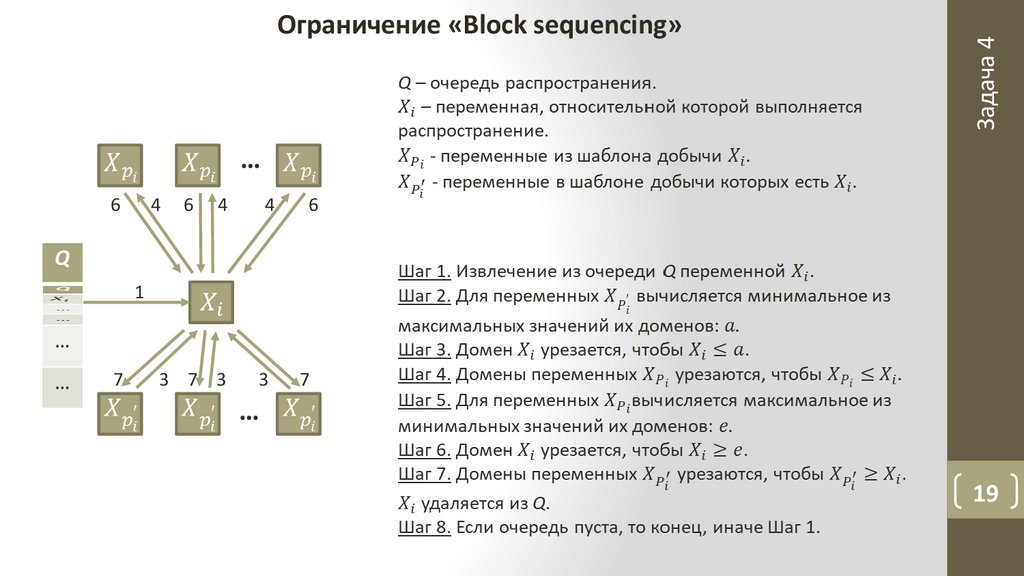
Задача 4
Ограничение «Block sequencing»
…
6
4
6
4
4
6
3 7 3
3
7
Q
1
…
…
7
…
19

20.

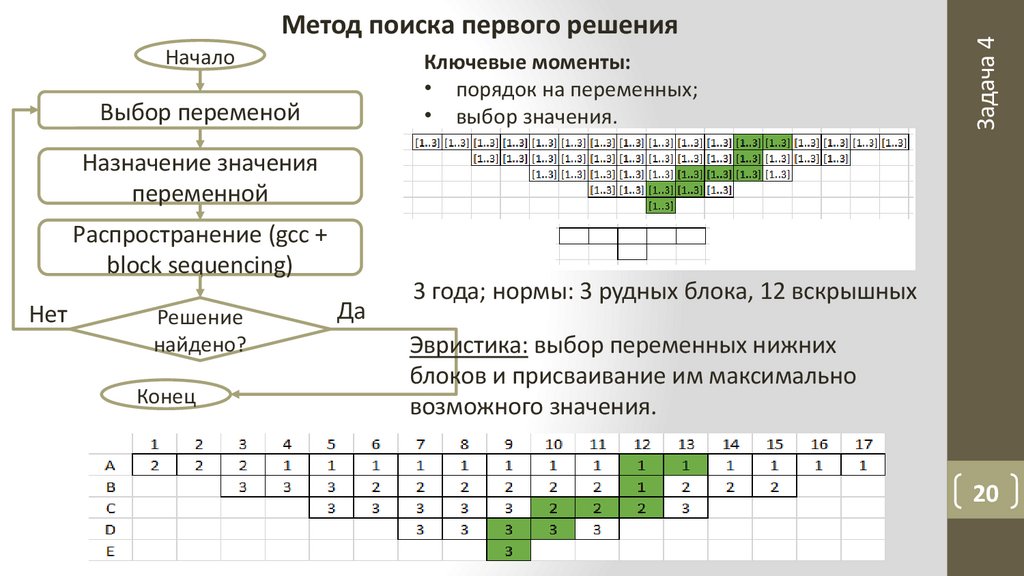
Начало
Ключевые моменты:
• порядок на переменных;
• выбор значения.
Выбор переменой
Задача 4
Метод поиска первого решения
Назначение значения
переменной
Распространение (gcc +
block sequencing)
Нет
Решение
найдено?
Конец
Да
3 года; нормы: 3 рудных блока, 12 вскрышных
Эвристика: выбор переменных нижних
блоков и присваивание им максимально
возможного значения.
20

21.

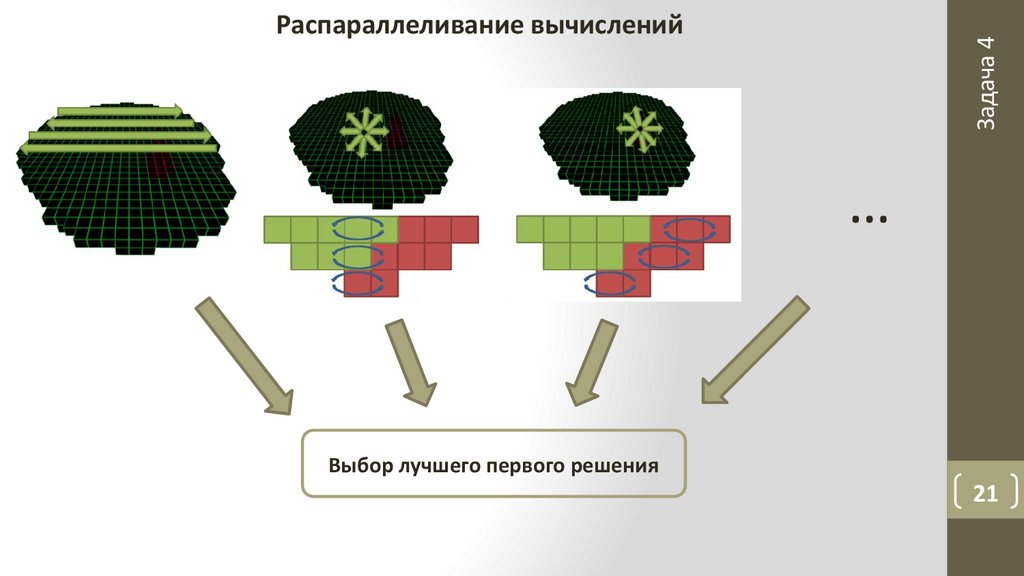
Задача 4
Распараллеливание вычислений
…
Выбор лучшего первого решения
21

22.

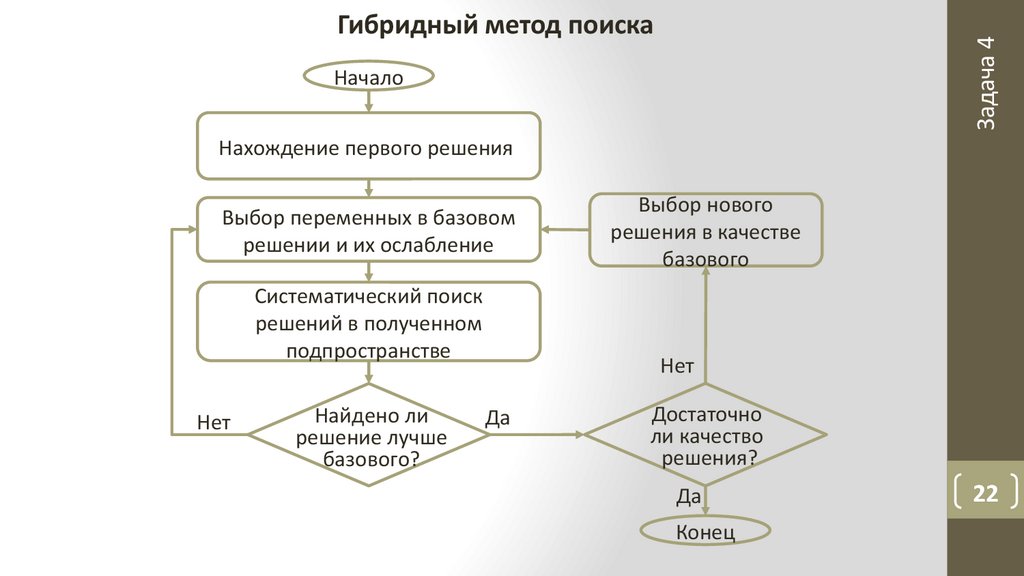
Задача 4
Гибридный метод поиска
Начало
Нахождение первого решения
Выбор переменных в базовом
решении и их ослабление
Систематический поиск
решений в полученном
подпространстве
Нет
Найдено ли
решение лучше
базового?
Выбор нового
решения в качестве
базового
Нет
Да
Достаточно
ли качество
решения?
Да
Конец
22

23.

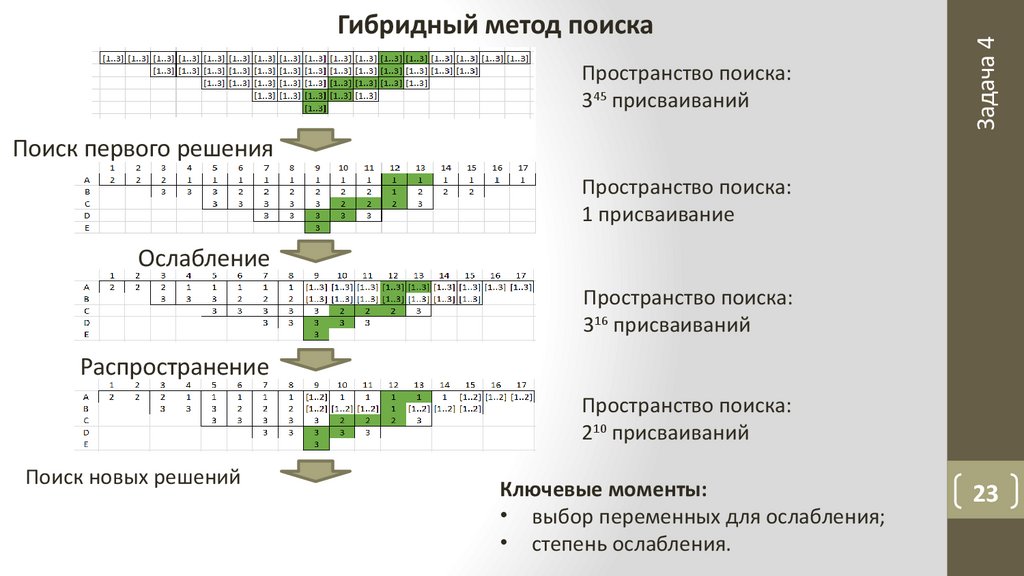
Пространство поиска:
345 присваиваний
Задача 4
Гибридный метод поиска
Поиск первого решения
Пространство поиска:
1 присваивание
Ослабление
Пространство поиска:
316 присваиваний
Распространение
Пространство поиска:
210 присваиваний
Поиск новых решений
Ключевые моменты:
• выбор переменных для ослабления;
• степень ослабления.
23

24.

Программный модуль для редукции размерности
задачи планирования открытых горных работ на
основе распространения ограничений
Задача 5
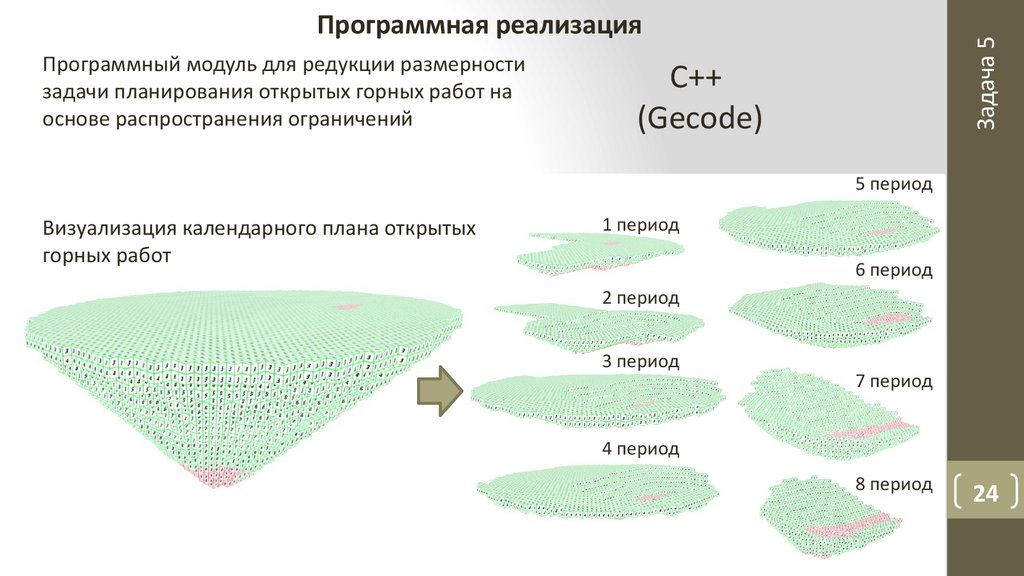
Программная реализация
C++
(Gecode)
5 период
Визуализация календарного плана открытых
горных работ
1 период
6 период
2 период
3 период
7 период
4 период
8 период
24

25.

Блочная модель содержит N блоков, технологические ограничения описываются M блоками,
T периодов планирования.
Линейное целочисленное программирование (Google OR-Tools):
Для N=4000, M=5, T=3 (12006 переменных, 64006 уравнений) решение найдено за 6 секунд.
Для N=4000, M=21, T=9 (36018 переменных, 760018 уравнений) – не найдено за 12 ч.
Задача 5
Вычислительные эксперименты
Fathollahzadeh K. et al. A mathematical model for open pit mine production scheduling with Grade Engineering® and stockpiling //
International Journal of Mining Science and Technology. 2021. Vol. 31. № 4. P. 717–728.
Программирование в ограничениях (систематический поиск):
Для N=4000, M=5, T=3 – первое решение за 2 минуты (80-95% от оптимального), далее
улучшалось до 95-98%.
Для N=4000, M=21, T=9 – первое решение за 10 минут, далее улучшалось.
Программирование в ограничениях с гибридным методом и тремя потоками поиска первого
решения:
Для N=4000, M=21, T=9 – первое решение за 2 секунды, далее улучшалось.
Для N=28000, M=21, T=9 – первое решение за 70 секунд, далее улучшалось.
Для N=82000, M=21, T=9 – первое решение за 15 минут, далее улучшалось.
Для N=535000, M=21, T=9 – первое решение за 8 часов, далее улучшалось.
25

26.

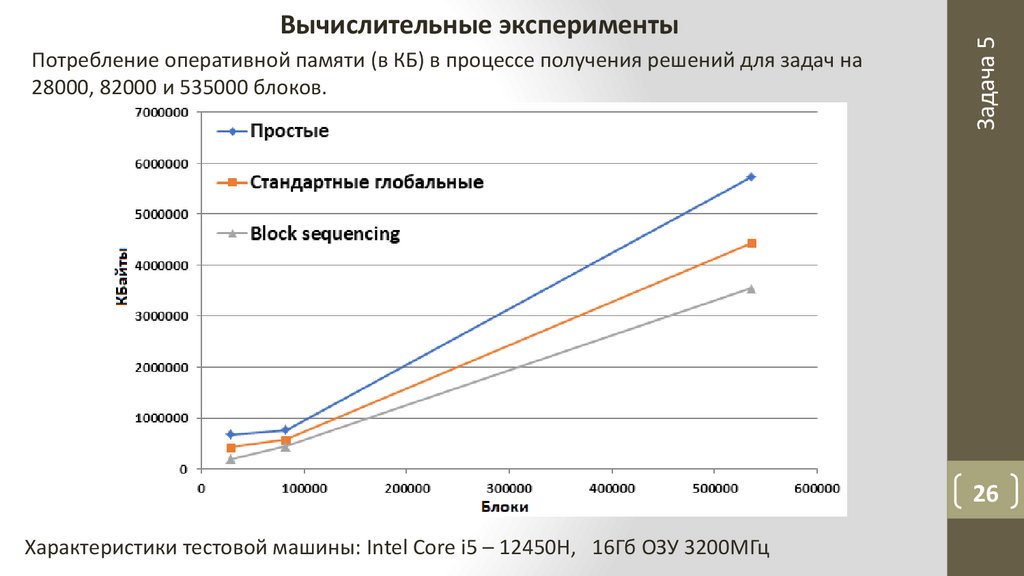
Потребление оперативной памяти (в КБ) в процессе получения решений для задач на
28000, 82000 и 535000 блоков.
Задача 5
Вычислительные эксперименты
26
Характеристики тестовой машины: Intel Core i5 – 12450H, 16Гб ОЗУ 3200МГц

27.

Публикации (ВАК)
1.
Зуенко А.А., Македонов Р.А., Олейник Ю.А. Интеллектуальный поиск точных решений задачи
планирования открытых горных работ // Системы анализа и обработки данных. – 2021. – № 3 (83).
– С. 99–114.
2.
Зуенко А.А., Олейник А.Г., Олейник Ю.А. Интеграция концептуального моделирования и
программирования в ограничениях для синтеза схем технологических процессов // Информационные
технологии и вычислительные системы. – 2022. – № 3. – С. 95–107.
3.
Олейник Ю.А., Зуенко А.А. Разработка глобального ограничения block sequencing при планировании
открытых горных работ // Информационные ресурсы России. – 2022. – № 3(187). – С. 33–45.
4.
Зуенко А.А., Олейник Ю.А. Составление расписаний как задача удовлетворения ограничений (на
примере планирования открытых горных работ). Информатика и автоматизация. – 2024. – № 23(5).
– С. 1290–1310. https://doi.org/10.15622/ia.23.5.1
5.
Зуенко А.А., Олейник Ю.А. Решения сложных задач комбинаторного поиска с использованием методов
удовлетворения ограничений (на примере среднесрочного планирования горных работ) // Вестник
Воронежского государственного университета. Серия: Системный анализ и информационные
технологии. – 2025. – № ???. (на рецензировании)
27

28.

Публикации (Scopus, WoS)
6.
Zuenko A., Oleynik Y. Constraint Programming Based on Matrix-like Representation of Qualitative
Constraints // Frontiers in Artificial Intelligence and Applications. Volume 312: Information Modelling and
Knowledge Bases XXX. 2019. P. 264–275.
7. Zuenko A., Oleynik Y. Programming of Algorithms of Matrix-Represented Constraints Satisfaction by Means of
Choco Library // Proceedings of the Third International Scientific Conference “Intelligent Information
Technologies for Industry” (IITI’18). 2019. Vol. 875. P. 439–448.
8. Zuenko A., Oleynik Y., Yakovlev S, Shemyakin A. Matrix-Like Representation of Production Rules in AI Planning
Problems // Proceedings of the Fourth International Scientific Conference “Intelligent Information
Technologies for Industry” (IITI’19). In: Advances in Intelligent Systems and Computing (AISC). 2020. Vol.
1156. P. 393–402.
9. Zuenko A., Oleynik Y., Makedonov R. A method for solving the open-pit mine production scheduling problem
using the constraint programming paradigm // Journal of Physics: Conference Series. 2021. Vol. 2060. N. 1. P.
012021.
10. Oleynik Y.A., Zuenko A.A. Open Pit Mine Production Scheduling using New Global Constraint // 2022 IEEE
International Multi-Conference on Engineering, Computer and Information Sciences (SIBIRCON). 2022. P.
1700–1704.
11. Zuenko A., Oleynik Y. Constraint Satisfaction Methods in Mining Planning. In: Kovalev, S., Sukhanov, A.,
Akperov, I., Ozdemir, S. (eds) Proceedings of the Ninth International Scientific Conference “Intelligent
Information Technologies for Industry” (IITI’25). 2025. Lecture Notes in Networks and Systems, vol ???.
Springer, Cham. (Scopus, в печати).
28

29.

Публикации
12. Олейник Ю.А., Зуенко А.А. Реализация алгоритмов удовлетворения нечисловых ограничений
средствами библиотек программирования в ограничениях // VIII-я Всероссийская научная
конференция “Теория и практика системной динамики”. Материалы конференции. – 2019.
– С. 123–127.
13. Олейник Ю.А., Зуенко А.А. Анализ возможностей совмещения парадигм программирования в
ограничениях и объектно-оринтированного программирования // Труды Кольского научного центра
РАН. – 2019. – № 9(9). – С. 109–115.
14. Олейник Ю.А., Зуенко А.А. Глобальные ограничения при моделировании и решении задач в рамках
парадигмы Constraint Programming // Труды Кольского Научного Центра Ран. – 2020. – № 8 (11).
– С. 67–83.
15. Зуенко А.А., Олейник Ю.А., Македонов Р.А. Планирование положений рабочего борта карьера по
периодам отработки в рамках парадигмы программирования в ограничениях // Труды Кольского
научного центра РАН. Информационные технологии. – 2021. – Вып. 12. – № 5. – С. 161–165.
16. Зуенко А.А., Олейник Ю.А., Македонов Р.А. Планирование положений рабочего борта карьера по
периодам отработки в рамках парадигмы программирования в ограничениях // Труды Кольского
научного
центра
РАН.
Информационные
технологии.
2021.
Вып.
12.
№
5.
С. 161–165.
29

30.

Публикации
17. Oleynik Y.A., Zuenko A.A. Open Pit Mine Production Scheduling using New Global Constraint // 2022 IEEE
International Multi-Conference on Engineering, Computer and Information Sciences (SIBIRCON). 2022.
P. 1700–1704.
18. Олейник Ю. А., Зуенко А. А. Два метода решения задачи планирования открытых горных работ // Труды
Кольского научного центра РАН. Серия: Технические науки. 2022. Т. 13. № 2. С. 111–115.
Регистрации программных продуктов
19. Зуенко А.А., Олейник Ю.А. Программный модуль для редукции размерности задачи планирования
открытых горных работ на основе распространения ограничений// Роспатент: Свидетельство о
государственной регистрации программы для ЭВМ № 2022683061 от 30 ноября 2022 г.
20. Зуенко А.А., Олейник Ю.А. Программа визуализации календарного плана открытых горных работ для
блочной модели карьера // Роспатент: Свидетельство о государственной регистрации программы для
ЭВМ № 2022681173 от 10 ноября 2022 г.
30

31.

Спасибо за
внимание!