Similar presentations:
ОКИ 1 семестр Лекция_5 (1)
1.
Кафедра стандартизации и метрологииКурс
Основы компьютерного
инжиниринга
Лектор: доцент, канд. техн. наук
Поликарпов Юрий Васильевич
2.
ОбразованиеУфимский авиационный институт, Механико-технологический факультет,
специальность Технология машиностроения, станки и инструменты
Аспирантура Московского авиационного института по специальности
Прикладная геометрия и инженерная графика
Достижения
Поликарпов Юрий
Васильевич
Доцент кафедры
стандартизации и метрологии
• Кандидат технических наук
• Доцент
• Область научных интересов – математическое моделирование
сложных технических поверхностей, твердотельное и
поверхностное моделирование изделий авиа- и машиностроения
3. Лекция №5. Позиционные задачи, изображения
1. Классификация геометрических задач.2. Общая схема решения задачи на построение линии пересечения двух
поверхностей.
3. Построение сечения поверхности плоскостью.
4. Сечения конуса вращения плоскостью (конические сечения).
5. Общая схема решения задачи на построение точек пересечения линии
с поверхностью.
6. Общие сведения об изображениях на чертежах.
7. Виды.
8. Сечения.
9. Разрезы.
10. Выносной элемент.
(учебники Гордона §§ 55-59, 67, Левицкого разделы 5.1 – 5.7)
3
4. 1. Классификация геометрических задач
Задачи, решаемые при проектировании геометрических объектов, принято делить на метрические и позиционные.В метрических задачах определяются различные геометрические величины: длины отрезков, углы, площади, объемы и т.п. Вы
уже изучили и знаете, например, как найти натуральную величину
отрезка прямой. К метрическим задачам также относят задачи на
построение разверток поверхностей.
Геометрические задачи, связанные с определением относительного расположения фигур в пространстве, называются позиционными.
© Поликарпов Ю.В
4
5. Позиционные задачи делятся на два типа:
1) задачи на определение взаимной принадлежности одногогеометрического объекта другому (например, построить точку на
прямой или на плоскости, построить прямую на плоскости,
построить линию на поверхности и т.п.).
2) задачи на нахождение точки или линии пересечения геометрических объектов между собой (построить линию пересечения двух поверхностей, построить линию пересечения поверхности с плоскостью, построить прямую пересечения двух плоскостей, построить точки пересечения линии с поверхностью,
построить точку пересечения прямой с плоскостью).
© Поликарпов Ю.В
5
6. 2. Общая схема решения задачи на построение линии пересечения двух поверхностей
В графических дисциплинах линию пересечения двух поверхностей находят с помощью приема, который называется способомвспомогательных секущих поверхностей (способ поверхностейпосредников). Этот способ заключается в следующем.
© Поликарпов Ю.В
6
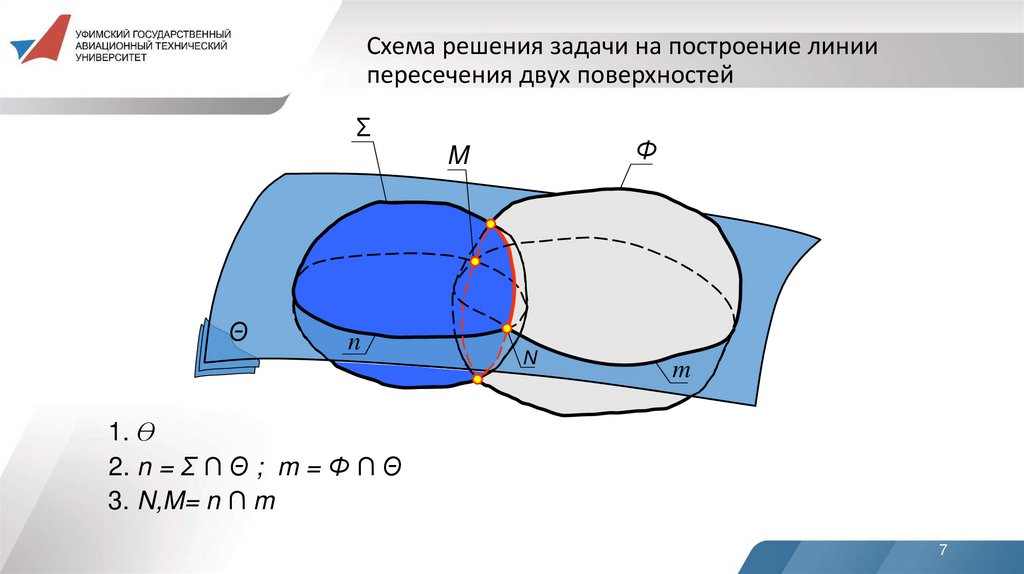
7. Схема решения задачи на построение линии пересечения двух поверхностей
ΣΦ
M
Θ
n
N
m
1. Ө
2. n = Σ ∩ Θ ; m = Φ ∩ Θ
3. N,M= n ∩ m
7
8.
На практике в качестве вспомогательных секущих поверхностейчаще всего используют плоскости (частный вид поверхности) или
сферы. В соответствии с этим из общего способа выделяются два,
которые называются способом плоскостей и способом сфер.
1) способ плоскостей применяют для построения точек линии пересечения двух поверхностей тогда, когда вспомогательные плоскости,
рассекающие эти поверхности, дают в пересечении с каждой из них
графически простые линии, такие как прямые или окружности; чаще
всего в качестве вспомогательных секущих плоскостей используют
проецирующие плоскости или плоскости уровня.
2) способ сфер применяют для построения точек линии пересечения
двух поверхностей вращения с общей плоскостью симметрии и
пересекающими осями.
8
© Поликарпов Ю.В
9. 3. Построение сечение поверхности плоскостью
Линия, которая получается от пересечения поверхности с плоскостью,является плоской кривой, лежащей в секущей плоскости. Чтобы
построить проекции этой линии на чертеже, находят проекции её отдельных точек и, соединяя одноимённые проекции точек плавными
кривыми (используя специальные кривые линейки для проведения
кривых линий – лекала), получают проекции искомой линии.
Сначала находят опорные точки, которые можно указать сразу, а затем
строятся остальные произвольные точки линии пересечения поверхности
с плоскостью. Находят их с помощью одного и того же приёма, который
является основным для решения рассматриваемой задачи. Этот приём
построения линии пересечения поверхности с плоскостью заключается в
применении вспомогательных секущих плоскостей.
© Поликарпов Ю.В
9
10.
В случае, когда с поверхностью пересекается проецирующая плоскость, решение задачи значительно упрощается. Это связано с тем, что вэтом случае становится известной одна проекция линии пересечения.
Она совпадает с проекцией проецирующей плоскости и располагается
внутри очерка поверхности. Поэтому остаётся построить лишь вторую
проекцию искомой линии. А для этого необходимо воспользоваться
вспомогательными линиями, лежащими на поверхности, что значительно проще, чем проводить вспомогательные плоскости.
Рассмотрим в качестве примера построение линии пересечения
сферы с фронтально-проецирующей плоскостью.
© Поликарпов Ю.В
10
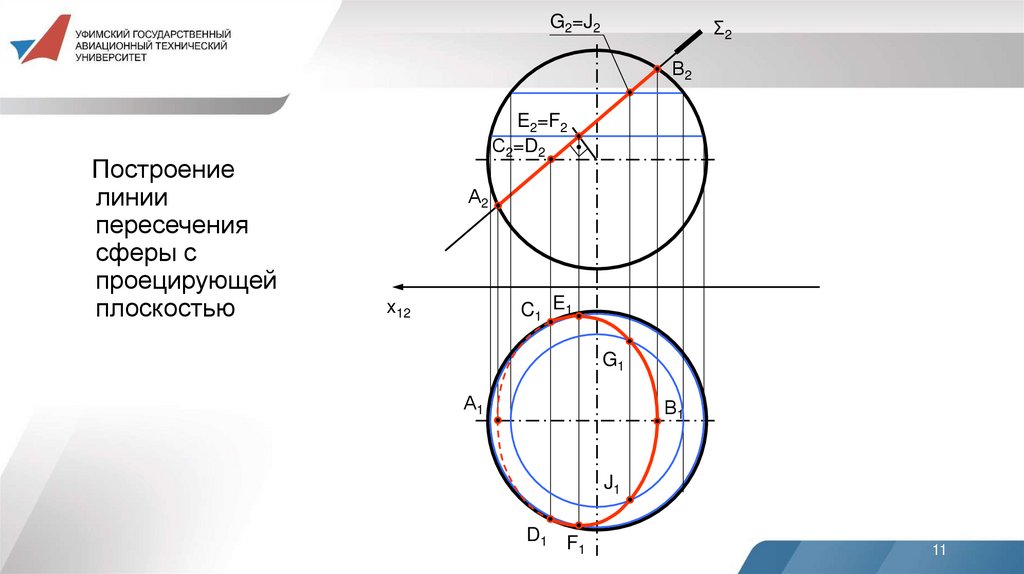
11.
G2=J2Σ2
В2
Построение
линии
пересечения
сферы с
проецирующей
плоскостью
E2=F2
С2=D2
А2
C1 E1
x12
G1
А1
В1
J1
D1 F
1
11
12. 4. Сечения конуса вращения плоскостью (конические сечения)
Две пересекающие прямыеГипербола
Парабола
Эллипс
Окружность
12
13. 5. Общая схема решения задачи на построение точек пересечения линии с поверхностью
Построения точек пересечения линии с какой-либо поверхностью выполняется с помощью вспомогательной поверхности. Задачарешается в следующей последовательности.
© Поликарпов Ю.В
13
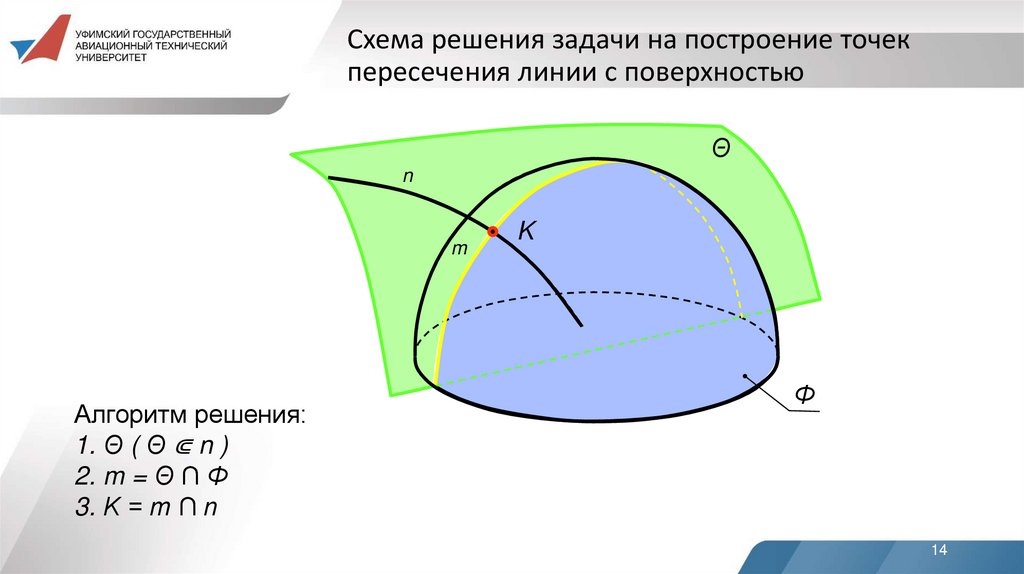
14. Схема решения задачи на построение точек пересечения линии с поверхностью
Θn
m
Алгоритм решения:
1. Θ ( Θ ⋐ n )
2. m = Θ ∩ Φ
3. K = m ∩ n
K
Φ
14
15.
В случае пересечения кривой линии с поверхностью в качестве вспомогательной поверхности используют проецирующую цилиндрическуюповерхность, которую проводят так, чтобы заданная кривая всеми точками
лежала на этой поверхности. На чертеже проецирующую цилиндрическую
поверхность задают одной своей проекцией, совпадающей с горизонтальной
проекцией линии, либо с фронтальной.
В случае пересечения прямой с поверхностью в качестве вспомогательной
поверхности используют плоскость. Сложность решения задачи во многом
зависит от сложности нахождения сечения поверхности вспомогательной
плоскостью. Поэтому в качестве вспомогательной необходимо использовать
плоскость, пересекающую поверхность по графически простым линиям. Чаще
всего применяются проецирующие плоскости.
© Поликарпов Ю.В
15
16.
6. Общие сведения об изображениях на чертежахПравила изображения предметов (изделий, сооружений и их составных элементов) на чертежах всех отраслей промышленности и строительства устанавливает
ГОСТ 2.305 - 2008.
Изображения предметов должны выполняться по
методу прямоугольного (ортогонального) проецирования.
16
17. Разновидности метода проецирования
Всего в мире используются две разновидности методапроецирования:
метод первого угла (метод Е), когда изображаемый предмет
располагается между наблюдателем и плоскостью проекций
(Россия, большинство стран Европы);
метод третьего угла (седьмого квадранта – метод А), когда
плоскость проекций располагают между наблюдателем и
изображаемым предметом (Англия, США и некоторые другие
страны).
17
18.
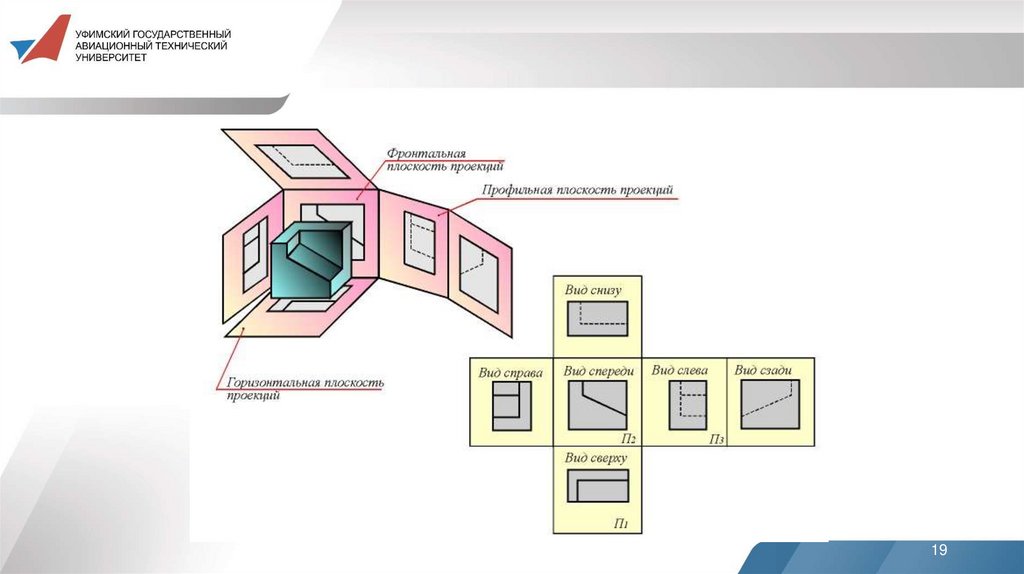
Метод ЕВ качестве основных плоскостей проекций принимают шесть
граней куба, которые затем совмещают с плоскостью.
Изображение на фронтальной плоскости принимается на
чертеже в качестве главного. Предмет располагают относительно
фронтальной плоскости проекций так, чтобы изображение на ней
давало наиболее полное представление о форме и размерах
предмета.
18
19.
1920.
Изображения на чертеже в зависимости отих содержания разделяются на виды, сечения,
разрезы, выносные элементы.
20
21.
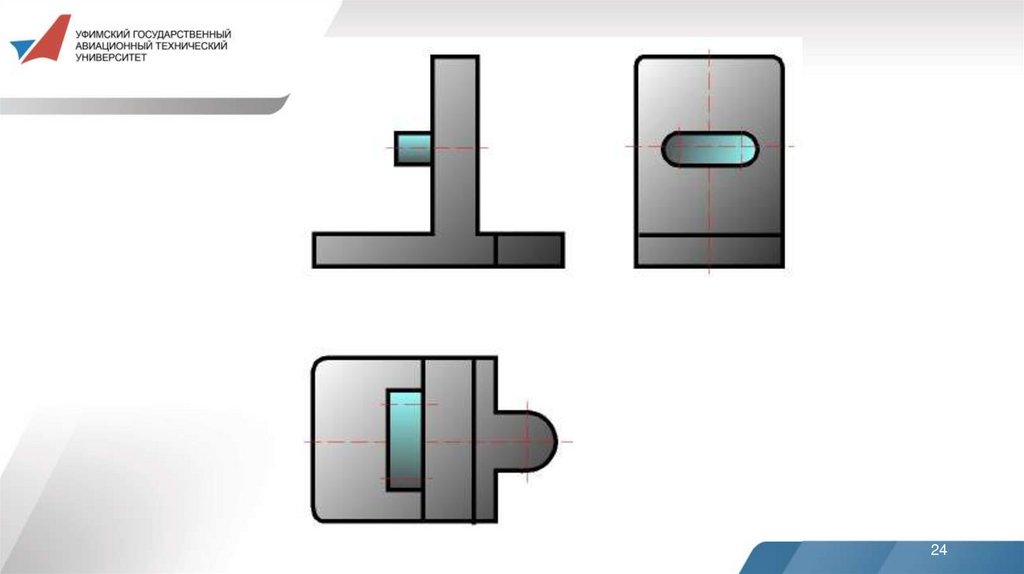
7. ВидыВид - изображение обращенной к наблюдателю
видимой части поверхности предмета.
На видах допускается показывать невидимые части
поверхности предмета при помощи штриховых линий.
Количество изображений должно быть наименьшим, но
обеспечивающим полное представление о предмете.
21
22.
Виды разделяются на основные, местные и дополнительные.Основные виды - изображения, получаемые на основных
плоскостях проекций - гранях куба:
1 - вид спереди (главный вид);
2 - вид сверху;
3 - вид слева;
4 - вид справа;
5 - вид снизу;
6 - вид сзади.
22
23.
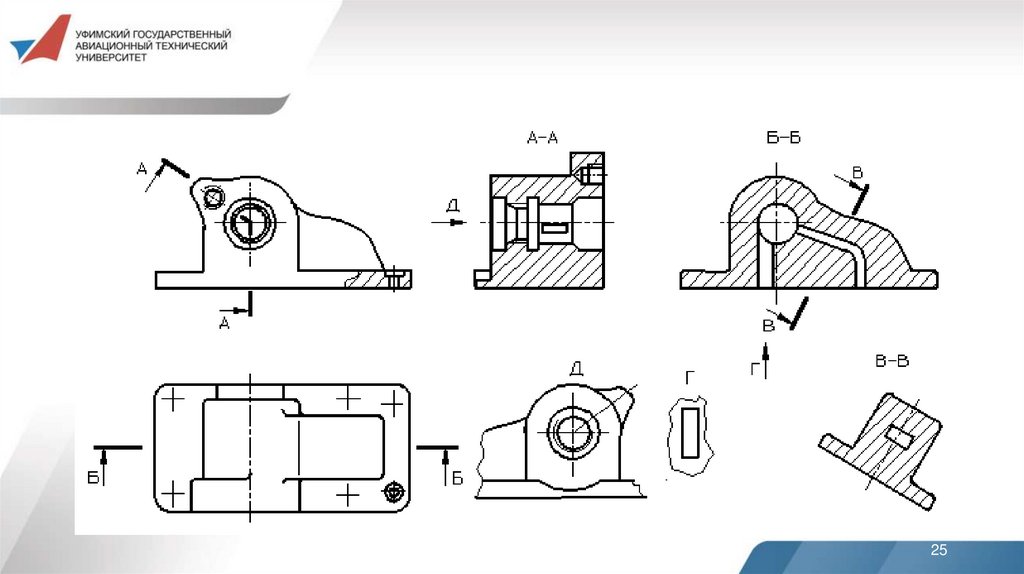
Название видов на чертежах не надписываются, еслиони расположены в проекционной связи.
Если же виды не находятся в проекционной связи с
главным изображением, то они отмечаются на чертеже
надписью по типу А. Направление взгляда указывается
стрелкой, обозначаемой прописной буквой русского
алфавита.
23
24.
2425.
2526.
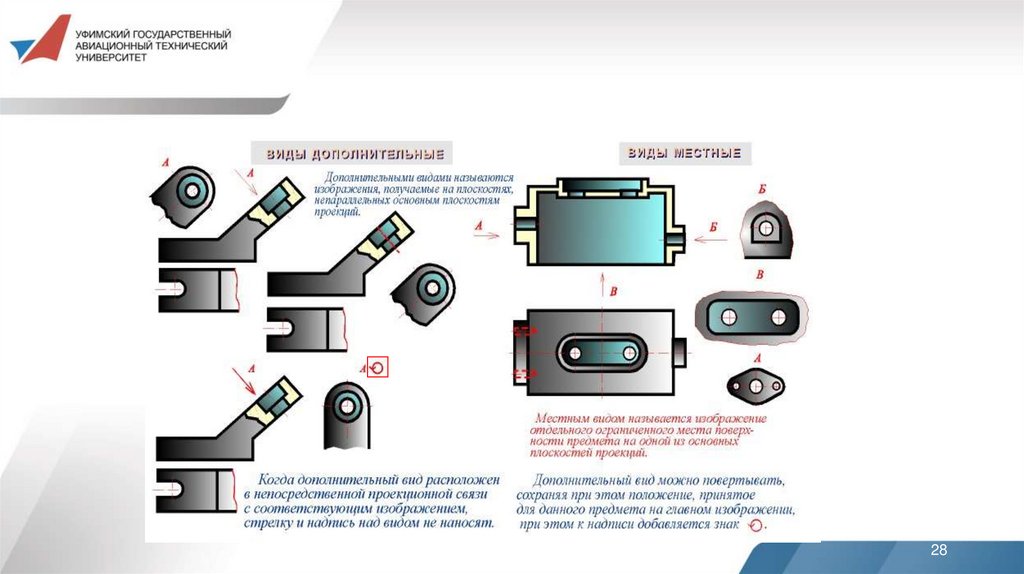
Местный вид - изображение отдельного ограниченногоместа поверхности предмета на одной из основных
плоскостей проекций. Местный вид можно располагать на
любом свободном месте чертежа, отмечая надписью типа
«А», а у связанного с ним изображения предмета должна
быть поставлена стрелка, указывающая направление
взгляда, с соответствующим буквенным обозначением.
26
27.
Дополнительные виды - изображения, получаемые наплоскостях, не параллельных основным плоскостям
проекций.
Применяются в тех случаях, если какую-либо часть
предмета невозможно показать на основных видах без
искажения формы и размеров.
Дополнительный вид должен быть отмечен на чертеже
прописной буквой и стрелкой, указывающей направление
взгляда.
27
28.
2829.
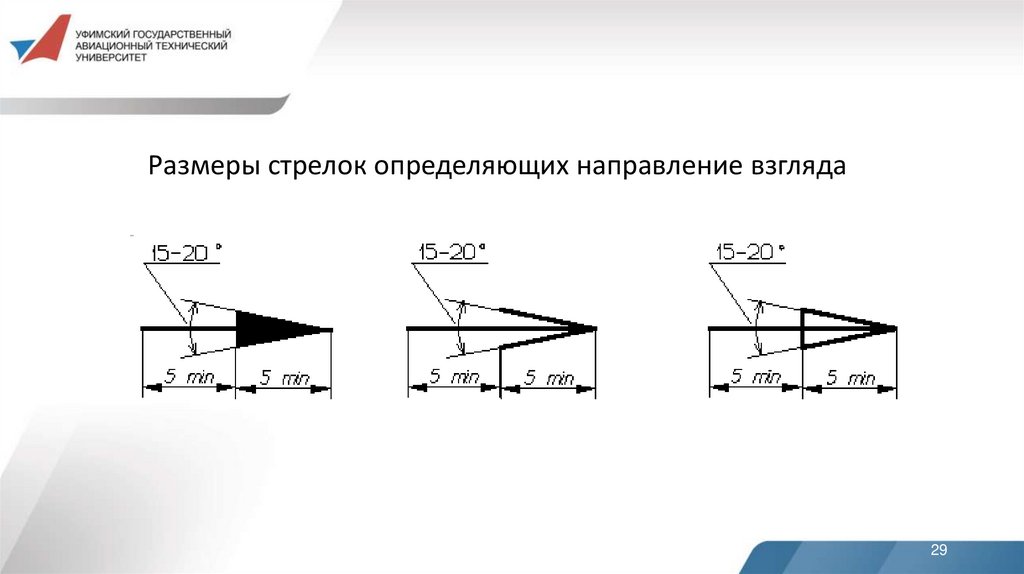
Размеры стрелок определяющих направление взгляда29
30.
Основные, местные и дополнительные виды служат дляизображения формы внешних поверхностей предмета. Удачное
их сочетание позволяет избежать штриховых линий или свести
их количество до минимума.
Выявление формы внутренних поверхностей предмета при
помощи штриховых линий значительно затрудняет чтение
чертежа, создает предпосылки для неправильного его
толкования, усложняет нанесение размеров и условных
обозначений. Поэтому для выявления внутренней (невидимой)
конфигурации предмета применяют условные изображения сечения и разрезы.
30
31.
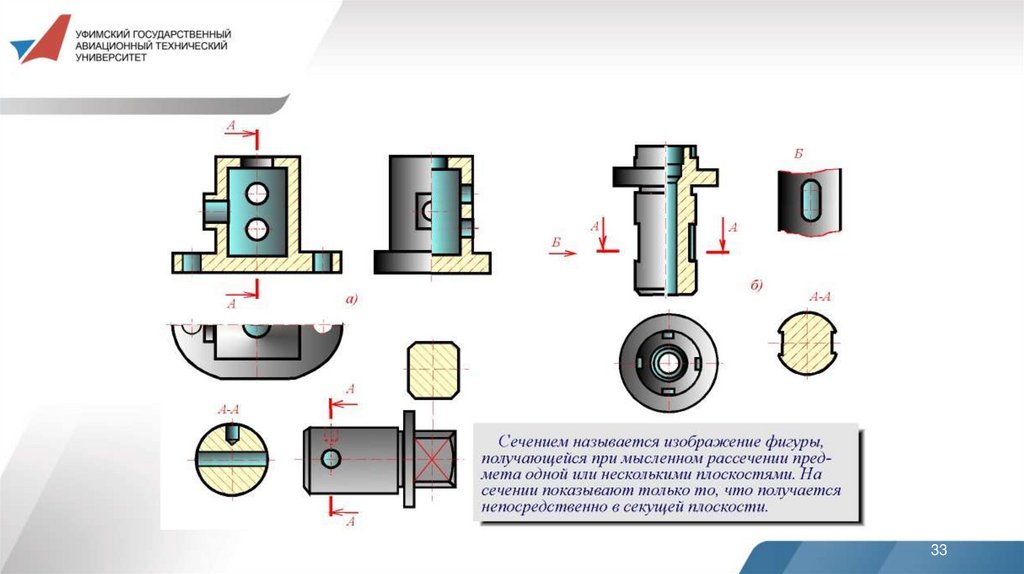
8. СеченияСечением называется изображение фигуры, получающейся при
мысленном рассечении предмета одной или несколькими
плоскостями. На сечении показывают только то, что получается
непосредственно в секущей плоскости.
Сечения делятся на:
входящие в состав разреза;
не входящие в состав разреза.
Сечения не входящие в состав разреза делятся на:
вынесенные;
наложенные.
31
32.
Вынесенные сечения являются предпочтительными и ихдопускается располагать:
в разрыве между частями одного и того же вида;
на продолжении следа секущей плоскости при симметричной фигуре сечения;
на любом месте поля чертежа, а также с поворотом.
32
33.
3334.
3435. Обозначение сечений
Положение секущей плоскости указывают на чертеже линиейсечения. Для линии сечения применяют разомкнутую линию со
стрелками, указывающими направление взгляда, и обозначают
секущую плоскость одинаковыми прописными буквами русского
алфавита. Сечение сопровождается надписью по типу А-А. Буквенные обозначения присваивают в алфавитном порядке без повторения и, как правило, без пропусков. Размер шрифта буквенных
обозначений должен быть больше размера цифр размерных чисел
приблизительно в два раза. Буквенное обозначение располагают
параллельно основной надписи, независимо от положения секущей
плоскости.
35
36.
При симметричной фигуре линию сечения не проводят исечение надписью не сопровождают. Для несимметричных
сечений, расположенных в разрыве, или наложенных, линию
сечения проводят со стрелками, но буквами не обозначают.
36
37. Выполнение сечений
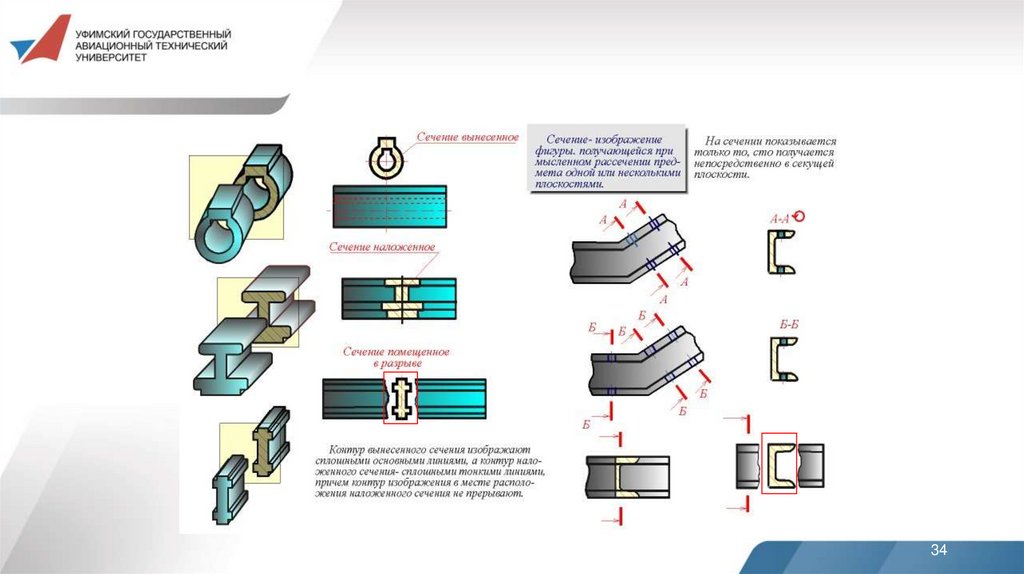
Контур вынесенного сечения, а также сечения, входящего всостав разреза, изображают сплошными основными линиями,
а контур наложенного сечения – сплошными тонкими линиями, причем контур изображения в месте расположения наложенного сечения не прерывают.
На чертеже сечения выделяют штриховкой. Вид ее зависит
от графического обозначения материала детали и должен
соответствовать ГОСТ 2.306 - 68.
37
38.
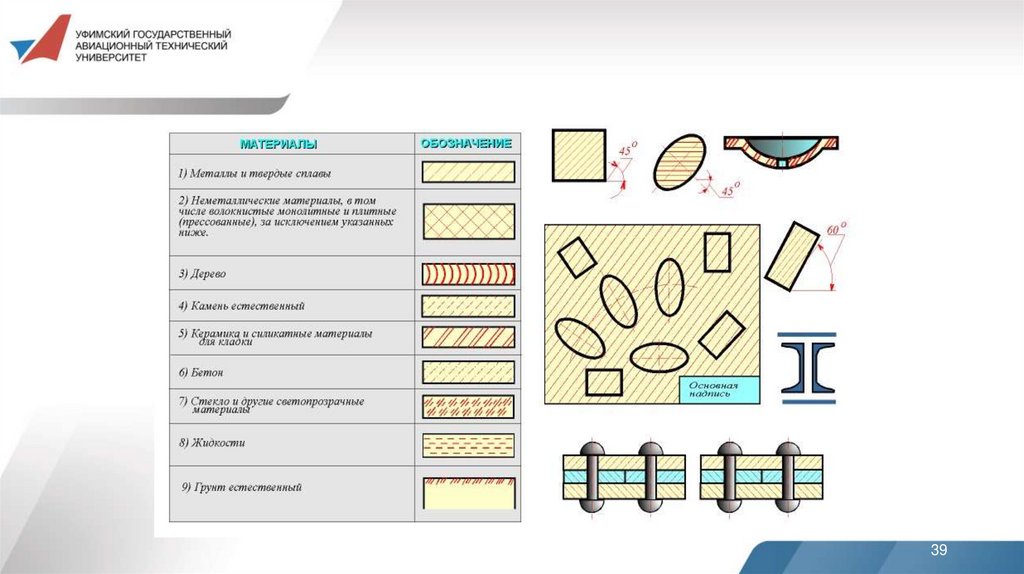
ГОСТ 2.306 - 68 «Обозначения графические материалови правила их нанесения на чертежах» устанавливает
графические обозначения материалов в сечениях за счет
различной штриховки. Её вид зависит от материала детали.
Металлы и твердые сплавы в сечениях обозначают наклонными параллельными линиями штриховки, проведенными под углом 45 к линии контура изображения (к его
оси или к линиям рамки чертежа). Неметаллы (пластмасса,
резина и т.п) в сечениях обозначают наклонными крестообразными линиями штриховки.
38
39.
3940.
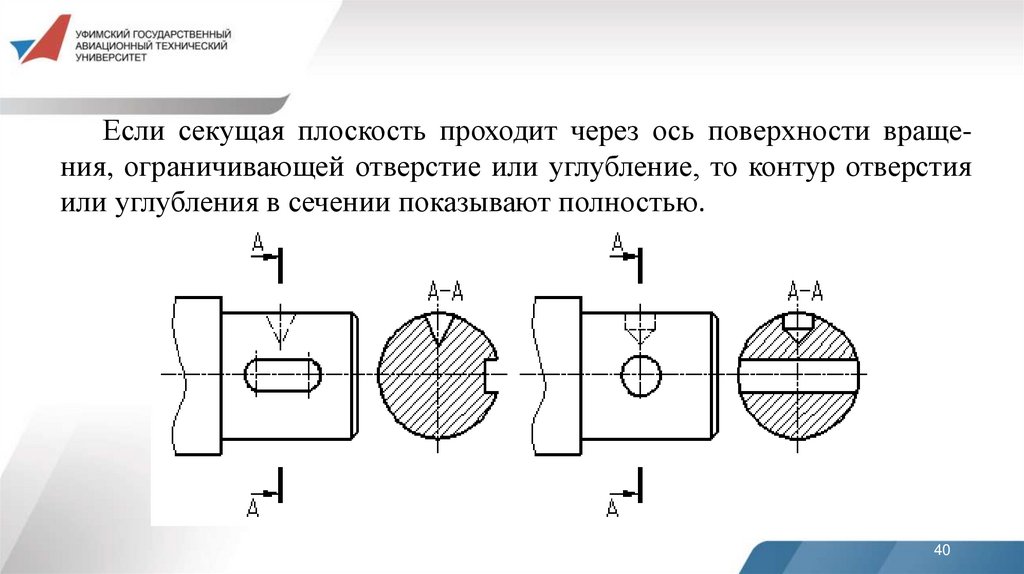
Если секущая плоскость проходит через ось поверхности вращения, ограничивающей отверстие или углубление, то контур отверстияили углубления в сечении показывают полностью.
40
41.
9. РазрезыРазрезом называется изображение предмета, мысленно рассеченного
одной или несколькими плоскостями. На разрезе показывают то, что
расположено в секущей плоскости и то, что расположено за ней.
41
42.
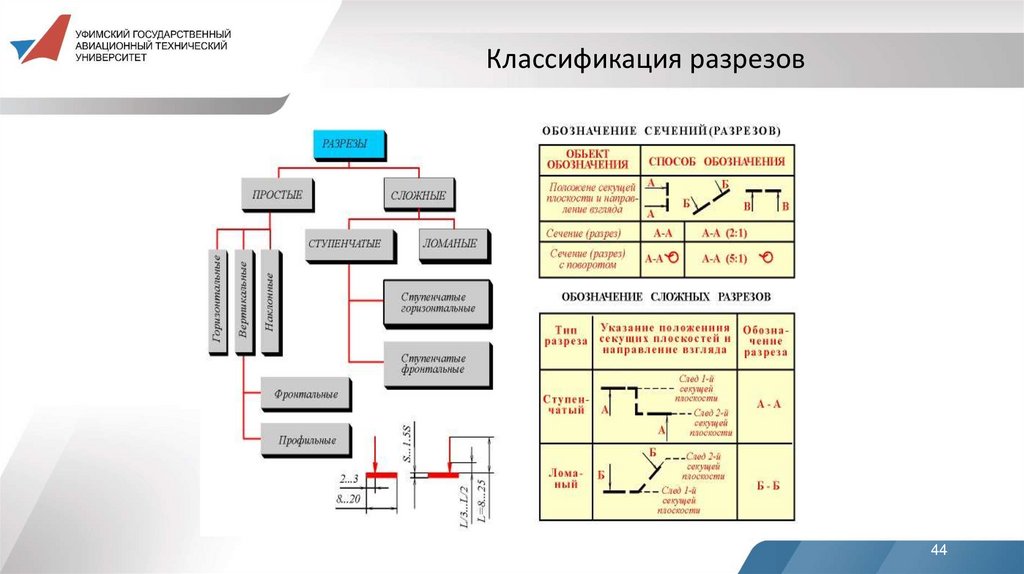
Классификация разрезовВ зависимости от числа секущих плоскостей pазpезы разделяются
на:
простые - при одной секущей плоскости;
сложные - при нескольких секущих плоскостях.
В зависимости от положения секущей плоскости pазpезы разделяются на:
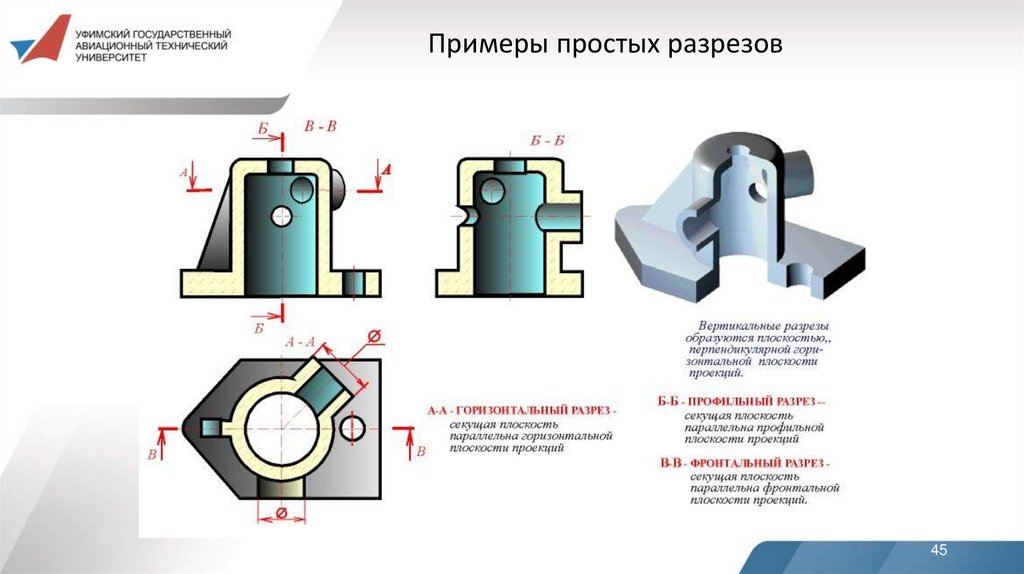
горизонтальные - секущая плоскость параллельна горизонтальной
плоскости проекций;
вертикальные - секущая плоскость пеpпендикуляpна горизонтальной плоскости проекций;
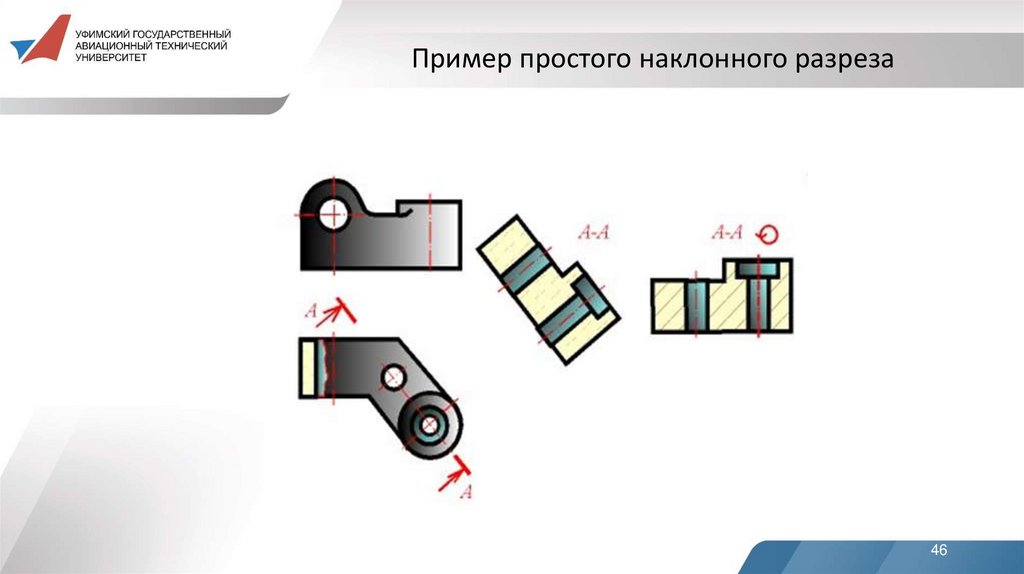
наклонные - секущая плоскость составляет с горизонтальной плоскостью проекций угол, отличный от прямого.
42
43.
Вертикальные pазpезы называются:фронтальными, если секущая плоскость параллельна фронтальной плоскости проекций;
профильными, если секущая плоскость параллельна профильной плоскости проекций.
Сложные разрезы разделяются на:
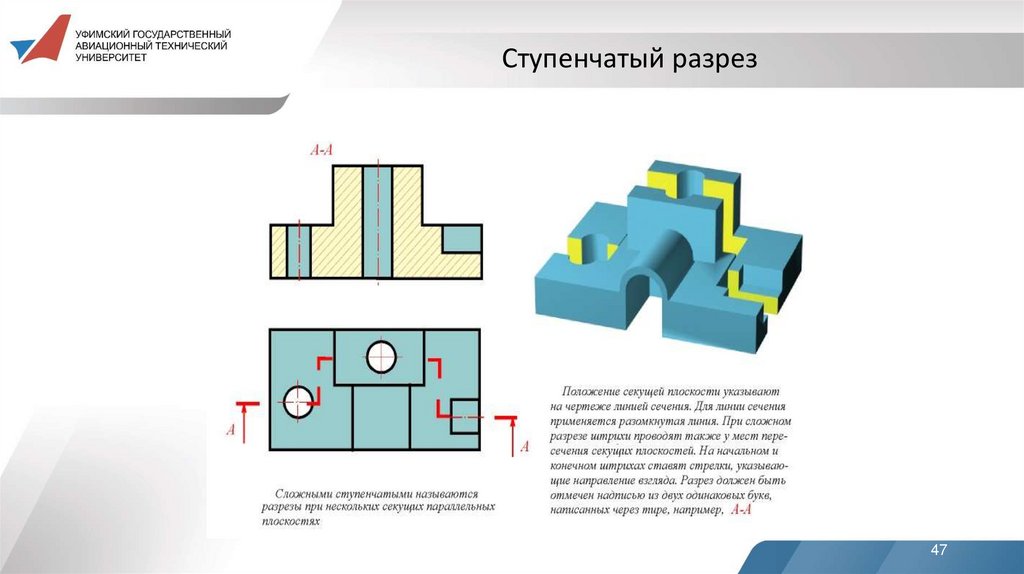
ступенчатые, если секущие плоскости параллельны (ступенчатые горизонтальные, ступенчатые фронтальные);
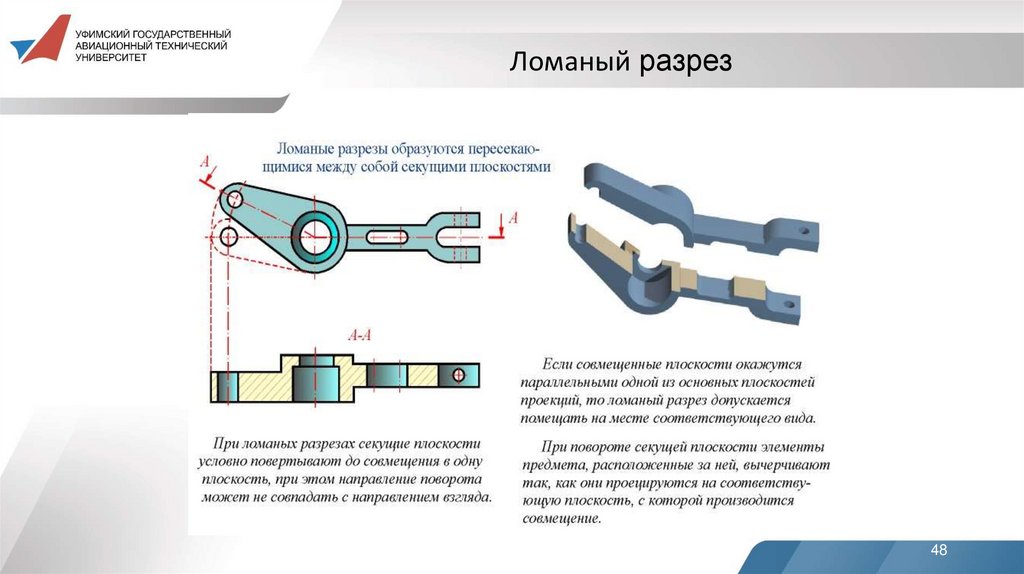
ломаные, если секущие плоскости пересекаются.
43
44. Классификация разрезов
4445.
Примеры простых разрезов45
46.
Пример простого наклонного разреза46
47.
Ступенчатый разрез47
48.
Ломаный разрез48
49.
Разрез, служащий для выяснения устройства предмета лишь в отдельном, ограниченном месте, называетсяместным.
Местный разрез выделяется на виде сплошной
волнистой линией или сплошной тонкой линией с
изломом.
49
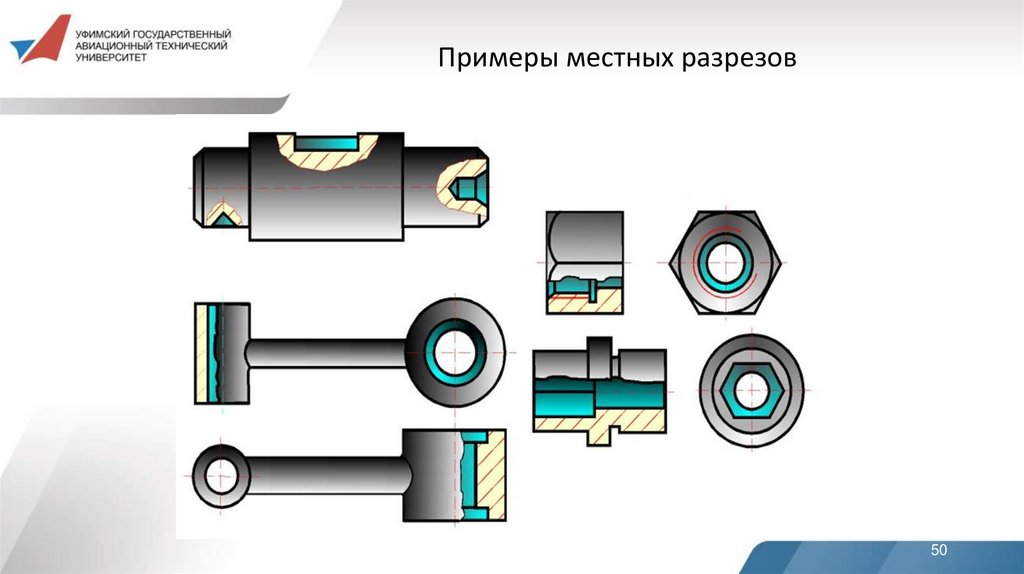
50.
Примеры местных разрезов50
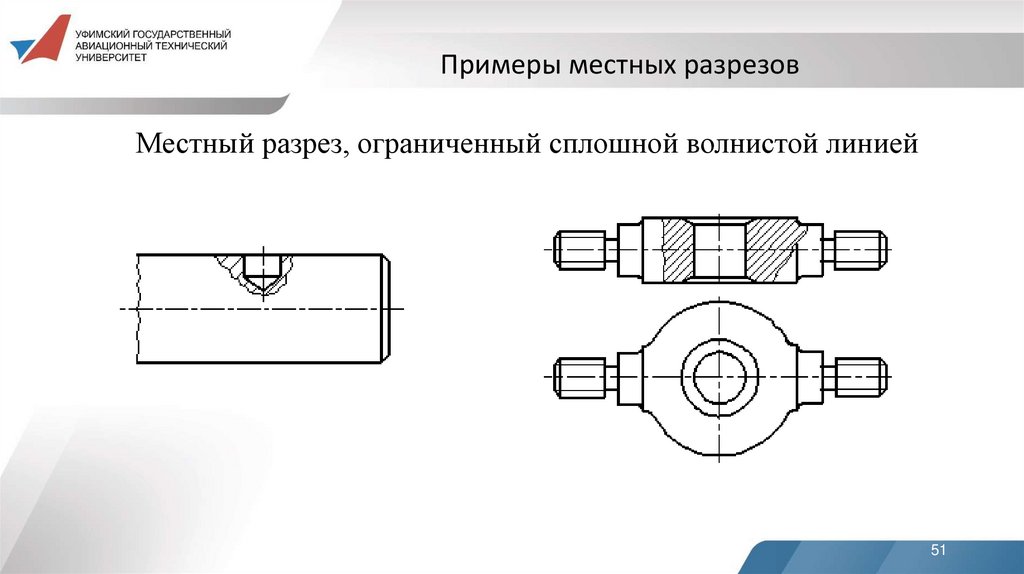
51.
Примеры местных разрезовМестный разрез, ограниченный сплошной волнистой линией
51
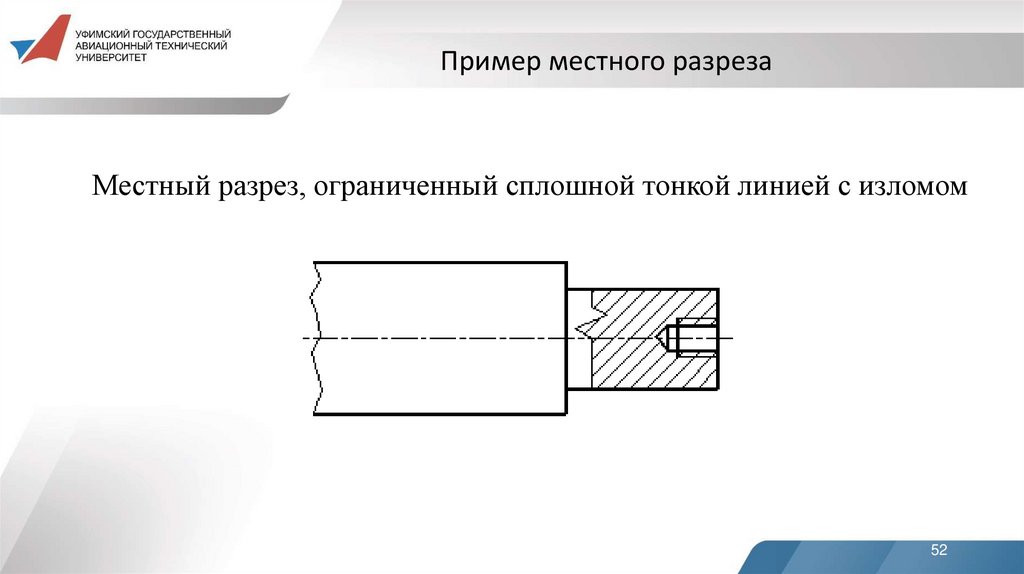
52.
Пример местного разрезаМестный разрез, ограниченный сплошной тонкой линией с изломом
52
53. Обозначение простых разрезов
Положение секущей плоскости не отмечают и разрез надписьюне сопровождают, если одновременно выполняются три условия:
1) секущая плоскость совпадает с плоскостью симметрии предмета в целом;
2) разрез расположен в непосредственной проекционной связи с
соответствующим изображением;
3) разрез является горизонтальным, фронтальным или профильным.
53
54.
Горизонтальные, фронтальные и профильные pазpезымогут быть расположены на месте соответствующих
основных видов.
Местные pазpезы выделяются на виде сплошными
волнистыми линиями. Эти линии не должны совпадать с
какими-либо другими линиями изображения.
54
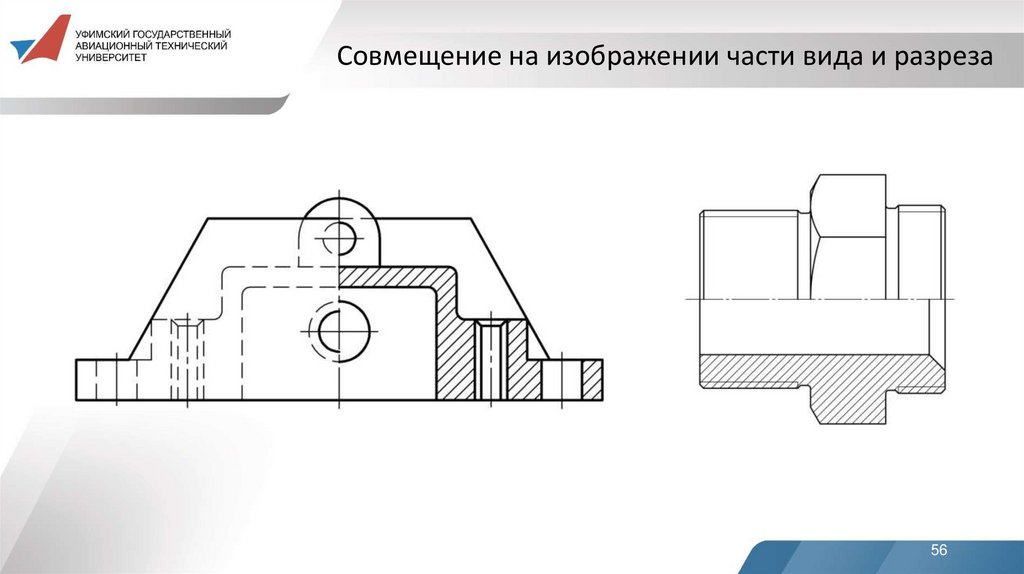
55.
Часть вида и часть соответствующего разреза допускается соединять, разделяя их сплошной волнистойлинией. Она не должна совпадать с какими-либо другими
линиями изображения. Если при этом соединяются
половина вида и половина разреза, каждый из которых
является симметричной фигурой, то разделяющей линией
служит ось симметрии.
55
56.
Совмещение на изображении части вида и разреза56
57.
Нельзя соединять половину вида с половиной разреза,если какая-либо линия изображения совпадает с осевой
(напpимеp, ребро). В этом случае соединяют большую
часть вида с меньшей частью разреза или большую часть
разреза с меньшей частью вида.
При соединении половины вида с половиной соответствующего разреза, разрез располагают справа от вертикальной оси и снизу от горизонтальной.
57
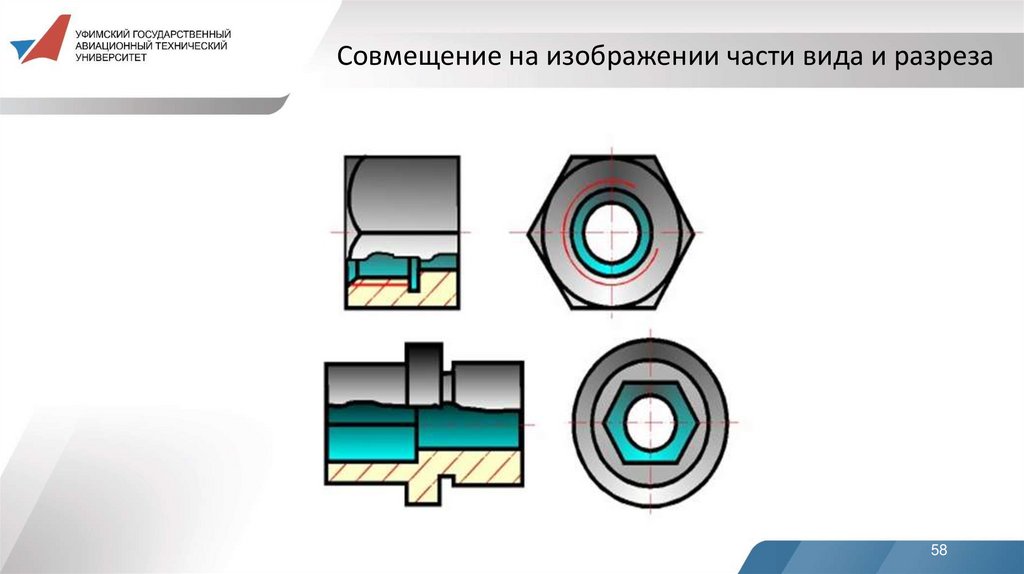
58.
Совмещение на изображении части вида и разреза58
59.
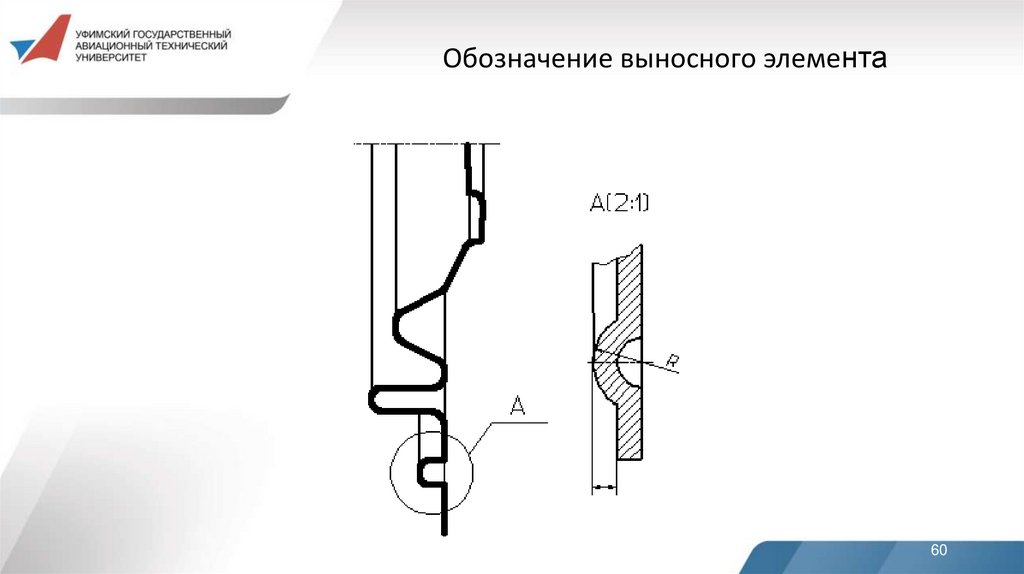
5. Выносной элементВыносной элемент – дополнительное отдельное изображение
(обычно увеличенное) какой-либо части предмета, требующей
графического и других пояснений в отношении формы, размеров и
иных данных.
При применении выносного элемента соответствующее место
отмечают на виде, разрезе или сечении замкнутой сплошной
тонкой линией. Обозначают выносной элемент прописной буквой
или сочетанием прописной буквы с арабской цифрой на полке
линии-выноски. Над изображением выносного указывают
обозначение и масштаб, в котором он выполнен.
59
60. Обозначение выносного элемента
6061. Заключение
Рассмотрев тему, мы:познакомились с классификацией геометрических задач;
изучили общую схему решения задач на построение линии пересечения
двух поверхностей, на построение сечения поверхности плоскостью, на
построение точек пересечения линии с поверхностью;
узнали какие кривые второго порядка можно получить пересекая конус
вращения различными плоскостями;
познакомились с двумя разновидностями проецирования, которые
применяются в различных странах;
узнали, что называется видом и какие применяются виды при выполнении
чертежей;
узнали, что называется сечением и разрезом, познакомились с
классификаций этих изображений;
познакомились с выносными элементами и узнали, как они оформляются
и обозначаются на чертежах.
© Поликарпов Ю.В
61
61
62.
СПАСИБО ЗА ВНИМАНИЕ!Поликарпов Ю.В.
https://www.ugatu.su/
450008, Республика Башкортостан,
г. Уфа, ул. К. Маркса, д. 12
+ 7 (987) 254-38-29
info@ugatu.su
62







































 drafting
drafting








