11_Відстані

1.

Комп’ютерна дискретна математика
Лекція 11
Н.В. Білоус
Факультет комп’ютерних наук
Кафедра ПІ, ХНУРЕ
ХНУРЕ, кафедра ПІ, e-mail: bilous.nataliya.nure.ua

2. Відстань. Аксіоми метрики

Нехай G - зв'язний граф, а u і v - дві його
неспівпадаючі вершини.
Довжина найкоротшого (u,v) - маршруту
називається відстанню між вершинами.
Аксіоми метрики:
1)d(u,v) 0, d(u,v)=0 тоді і тільки тоді, коли u=v,
2) d(u,v)=d(v,u),
3) d(u,v)+d(v,w) d(u,w)
2

3. Відстань між двома вершинами на графі

У деяких графах ребрам приписані числові
характеристики (пропускна здатність, ціна,
вага, довжина).
У цих випадках довжиною ланцюга є сума
числових характеристик ребер, що входять в
ланцюг.
Відстанню між a і b буде довжина
найкоротшого ланцюга.
3

4. Відстань між двома вершинами на графі

Приклад.
Визначити відстань між ребрами a і b неорієнтованого
графа із заданими числовими характеристиками ребер.
Рішення.
S1(a,b)=(a,v3,v4,v5,b)=10;
S2(a,b)=(a,v1,v2,b)=17;
S3(a,b)=(a,v2,b)=19;
S4(a,b)=(a,v1,v2,v5,b)=15;
S5(a,b)=(a,v3,v4,v5,v2,b)=30;
S6(a,b)=(a,v2,v5,b)=17.
Найкоротша довжина S1(a,b)=10.
Тоді d(a,b)=10.
4

5. Алгоритм Дейкстра

Алгоритм
Дейкстри
виконується
шляхом
знаходження довжини найкоротшого шляху від a до
першої вершини, довжини найкоротшого шляху від a
до другої вершини, поки не буде знайдена довжина
найкоротшого шляху від a до z.

6. Алгоритм Дейкстра

1) Позначення a з 0, а інші вершини з ∞:
L0 (a) = 0
L0 (vi ) = ∞.
Ці позначки є довжиною найкоротших шляхів
від a до вершин, де шляхи містять лише вершину
a.

7. Алгоритм Дейкстра

2) Нехай Sk це набір вершин після k ітерацій
процедури розмітки. S0 = . Набір Sk утворюється
з Sk-1 додаванням вершини u в Sk-1 з найменшою
позначкою.. Як тільки u додано до Sk, ми
оновлюємо позначки всіх вершин, не в Sk, так що
Lk(v), позначка вершини v на k-му етапі, є
довжиною найкоротшого шляху від a до v, що
містить вершини лише на Sk .

8. Алгоритм Дейкстра

3) Нехай v - вершина, що не знаходиться в Sk. Щоб
оновити позначку v, зверніть увагу на те, що Lk (v)
- довжина найкоротшого шляху від a до v, що
містить лише вершини в Sk. Найкоротший шлях
від a до v, що містить лише елементи Sk - це або
найкоротший шлях від a до v, що містить лише
елементи Sk-i або це найкоротший шлях від a до u
на етапі (k -1) з додаванням ребра (u, v). Іншими
словами
Lk (a,v) = min{L k-1 (a, v), L k-1 (a,
u)+ w(u, v)}

9. Алгоритм Дейкстра

4) Коли z додається до виділеного набору, його
позначка - це довжина найкоротшого шляху від a
до z.

10. Процедура алгоритму Дейкстра

процедура Дейкстра (G: зважений зв'язаний простий граф, з усіма
додатними вагами){G має вершини a = v0, v1,…, vn = z і ваги w (vi, vj), де w
(vi, vj) = ∞, якщо {vi, vj} не є ребром у G}
for i: = 1 to n
L (vi) : = ∞
L (a) : = 0
S : = {позначки тепер ініціалізовані так, що позначка a дорівнює нулю, а всі інші позначки ∞, а S порожній набір}.
while z S почати
u : = вершина не в S з L (u) мінімальною
S:=S {u}
для всіх вершин v не в S
if L(u) + w(u, v) < L(v) then L(v): =L(u) + w(u, v)
{це додає вершину до S з мінімальною позначкою та оновлює позначки вершин, не в S}
end {L(z) = довжина найкоротшого шляху від a до z}

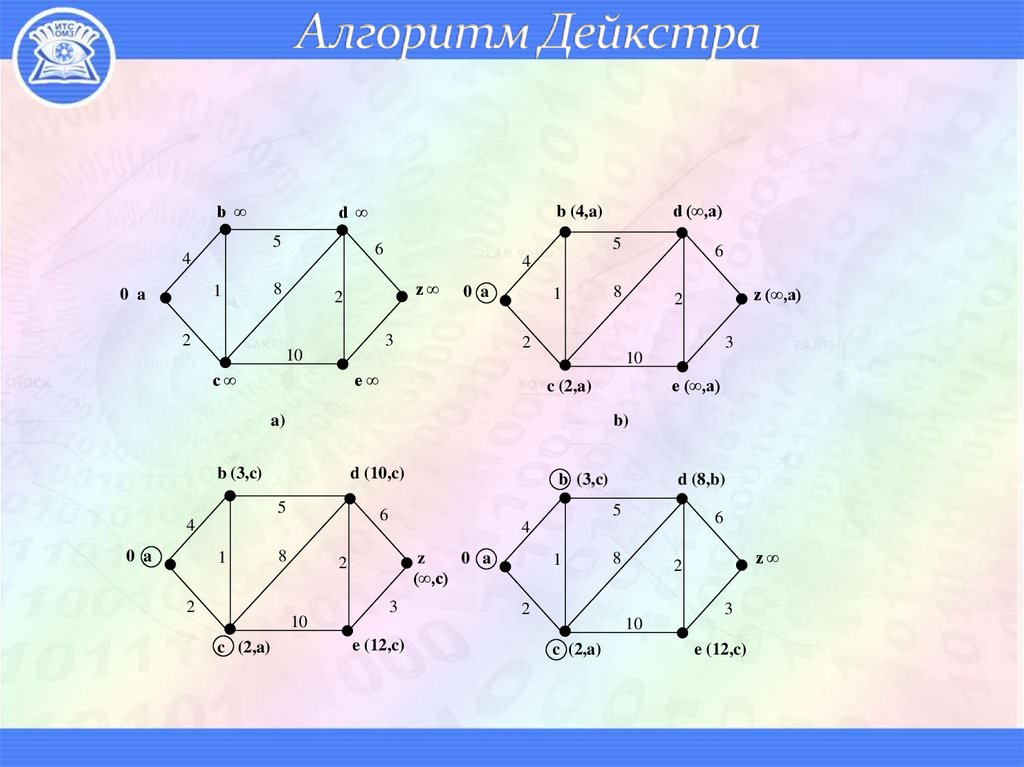
11. Алгоритм Дейкстра

b ∞
d ∞
5
1
0 a
5
6
4
8
z∞
0 a
3
1
z (∞,a)
2
3
10
c∞
e∞
e (∞,a)
c (2,a)
a)
b)
b (3,c)
d (10,c)
5
b (3,c)
8
6
4
0 a
z
(∞,c)
2
2
d (8,b)
5
6
4
3
10
c (2,a)
8
2
10
1
6
4
2
2
0 a
d (∞,a)
b (4,a)
1
8
z∞
2
2
3
10
e (12,c)
c (2,a)
e (12,c)

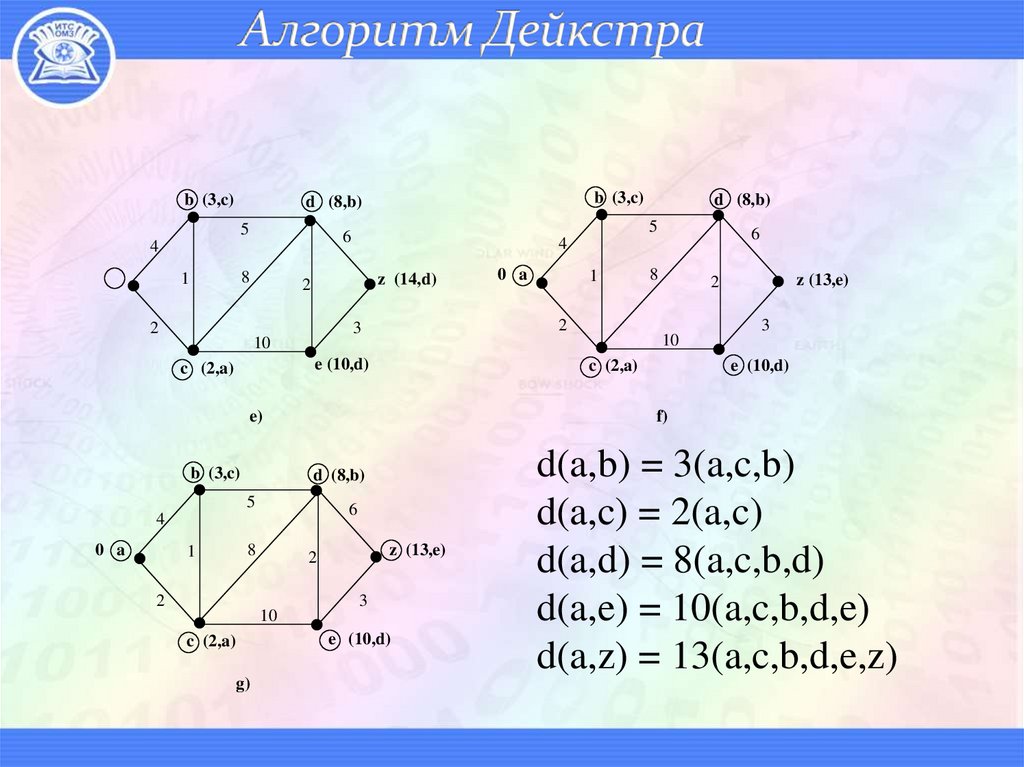
12. Алгоритм Дейкстра

b (3,c)
b (3,c)
d (8,b)
5
8
1
5
6
4
2
z (14,d)
d (8,b)
5
1
6
8
z (13,e)
2
2
3
10
e (10,d)
c (2,a)
g)
8
z (13,e)
2
10
3
e (10,d)
f)
4
0 a
1
c (2,a)
e)
b (3,c)
0 a
2
3
e (10,d)
c (2,a)
6
4
2
10
d (8,b)
d(a,b) = 3(a,c,b)
d(a,c) = 2(a,c)
d(a,d) = 8(a,c,b,d)
d(a,e) = 10(a,c,b,d,e)
d(a,z) = 13(a,c,b,d,e,z)

13. Алгоритм Дейкстри визначення відстані між вершинами на графі з довільними довжинами ребер

Крок
1.
(Привласнення
початкових
значень).Покласти l (s) = 0 і вважати цю позначку
постійною (тобто - пофарбувати вершину).
Покласти l(w)= для всіх вершин, і вважати ці
позначки тимчасовими.
Покласти p = s (p -ім'я останньої вершини, що
отримала постійну позначку).
13

14. Алгоритм Дейкстри визначення відстані між вершинами на графі з довільними довжинами ребер

Крок 2. (Оновлення позначок).
Для кожної непофарбованої вершини w, в яку веде
дуга (p, w) з вершини p, позначка l (w) змінюється
за правилом
14

15. Алгоритм Дейкстри визначення відстані між вершинами на графі з довільними довжинами ребер

Крок
3.
(Перетворення
позначки
в
постійну).На безлічі всіх непофарбованих
вершин (з тимчасовими позначками)
Wp
знайти вершину w0 з мінімальною позначкою:
l ( w0 ) min{ l ( w)}
w W p
Зробити позначку
l(w0)
постійною і покласти p = w0.
вершини
w0
15

16. Алгоритм Дейкстри визначення відстані між вершинами на графі з довільними довжинами ребер

Крок 4. (Якщо треба знайти лише
найкоротший шлях від s до t).
4.а. Якщо p = t, то l (p) - довжина
найкоротшого (s, t) -шляху.
Зупинка.
4.б. Якщо p ≠ t, то перейти до кроку 2.
16

17. Алгоритм Дейкстри визначення відстані між вершинами на графі з довільними довжинами ребер

Крок 5. (Якщо потрібно знайти найкоротші
шляхи від s до всіх вершин графа G).
Алгоритм виконується так довго, щоб всі вершини
отримали
постійні
позначки,
і
безліч
непофарбованих вершин вичерпалася:
.
. W p 0 Зупинка.
Приклад визначення відстані між вершинами на графі з
довільними довжинами ребер
17