Similar presentations:
Логика
1.
Логика. Построениетаблиц истинности
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ИНФОРМАТИКИ
2.
Ключевые слова• алгебра логики
• высказывание
• логическая операция
• конъюнкция
• дизъюнкция
• отрицание
• логическое выражение
• таблица истинности
• законы логики
3.
Высказывание- объект алгебры логикиВысказывание - это предложение на
любом языке, содержание которого можно
однозначно определить как истинное или
ложное.
В
русском
языке
высказывания
выражаются
повествовательными предложениями:
Земля вращается вокруг Солнца.
Москва - столица.
Побудительные и вопросительные
предложения высказываниями не
являются.
Без стука не входить!
Откройте учебники.
Ты выучил стихотворение?
4.
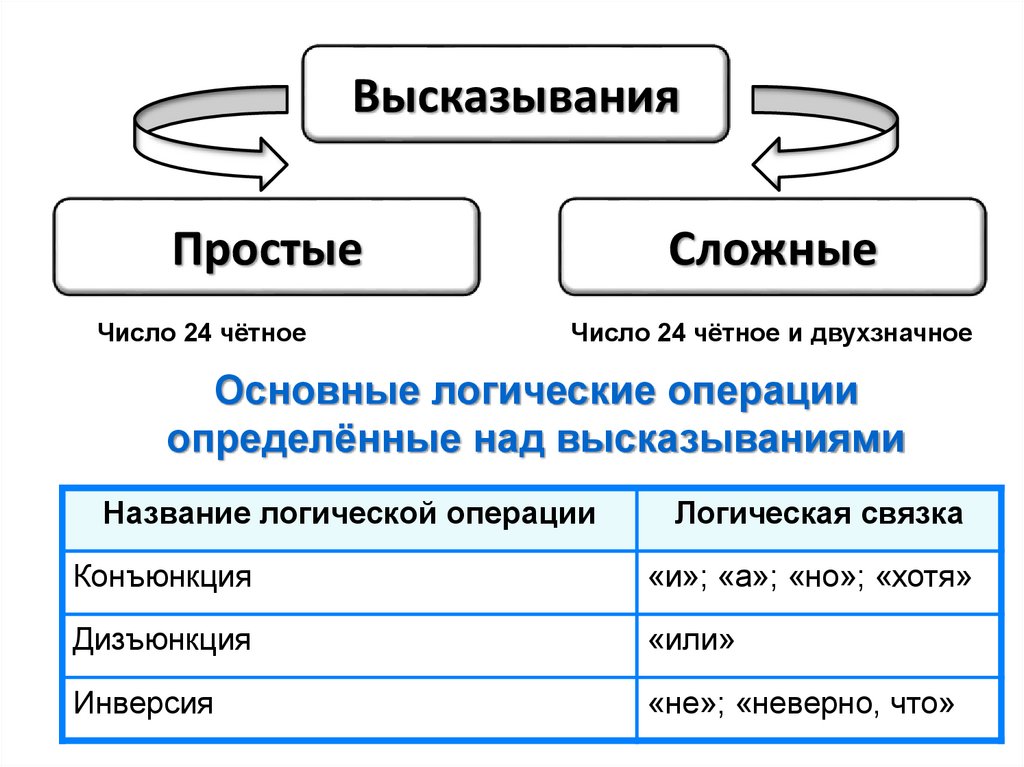
ВысказыванияПростые
Число 24 чётное
Сложные
Число 24 чётное и двухзначное
Основные логические операции
определённые над высказываниями
Название логической операции
Логическая связка
Конъюнкция
«и»; «а»; «но»; «хотя»
Дизъюнкция
«или»
Инверсия
«не»; «неверно, что»
5.
Алгебра логикиАлгебра логики определяет правила записи, вычисления значений,
упрощения и преобразования высказываний.
В алгебре логики высказывания обозначают буквами и называют логическими переменными.
1- Истинное высказывание
0 - Ложное высказывание
6.
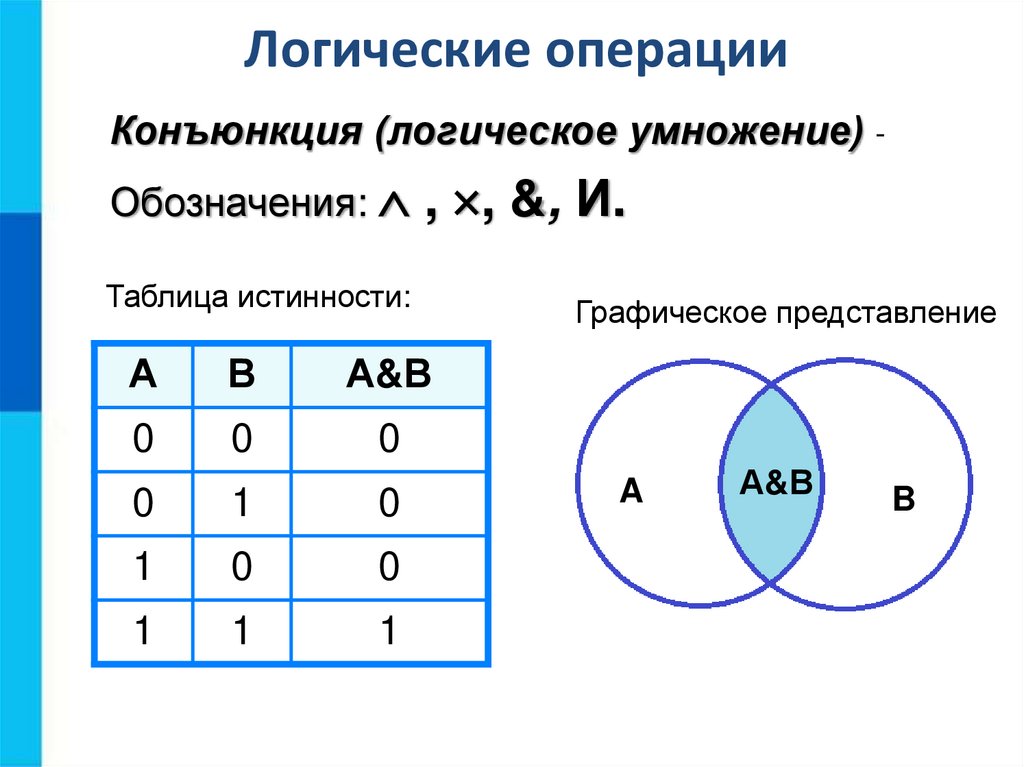
Логические операцииКонъюнкция (логическое умножение) Обозначения: , , &, И.
Таблица истинности:
А
В
А&В
0
0
0
0
1
0
1
0
0
1
1
1
Графическое представление
A
А&В
B
7.
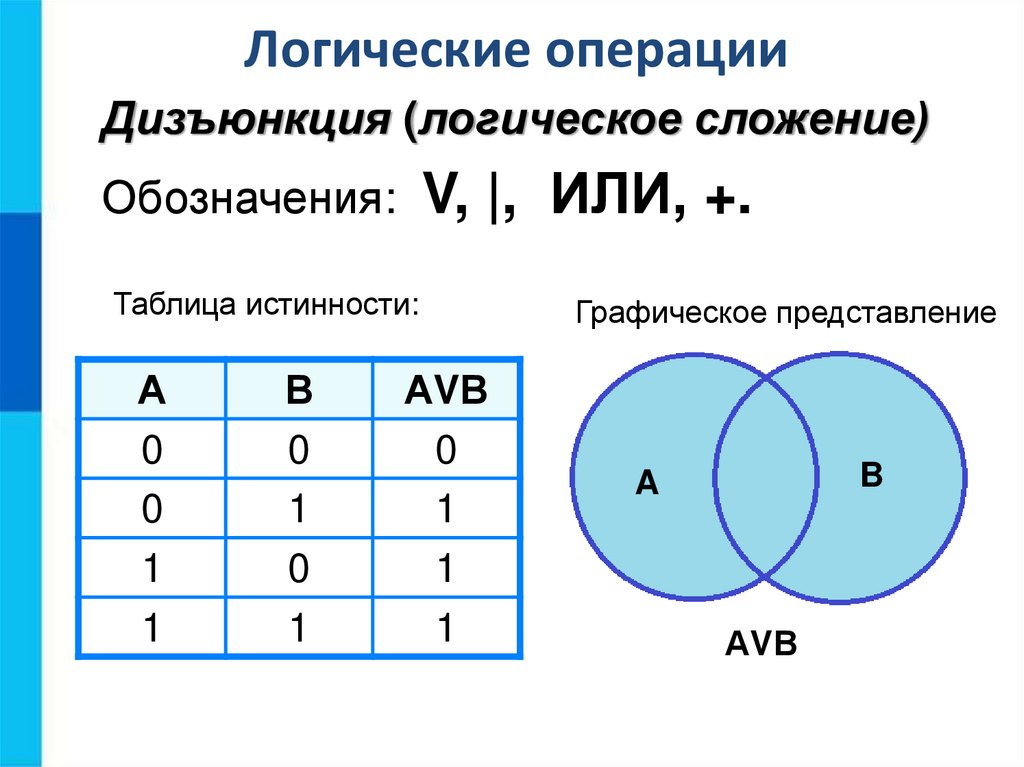
Логические операцииДизъюнкция (логическое сложение)
Обозначения: V, |, ИЛИ, +.
Таблица истинности:
А
0
0
1
1
В
0
1
0
1
АVВ
0
1
1
1
Графическое представление
B
A
АVВ
8.
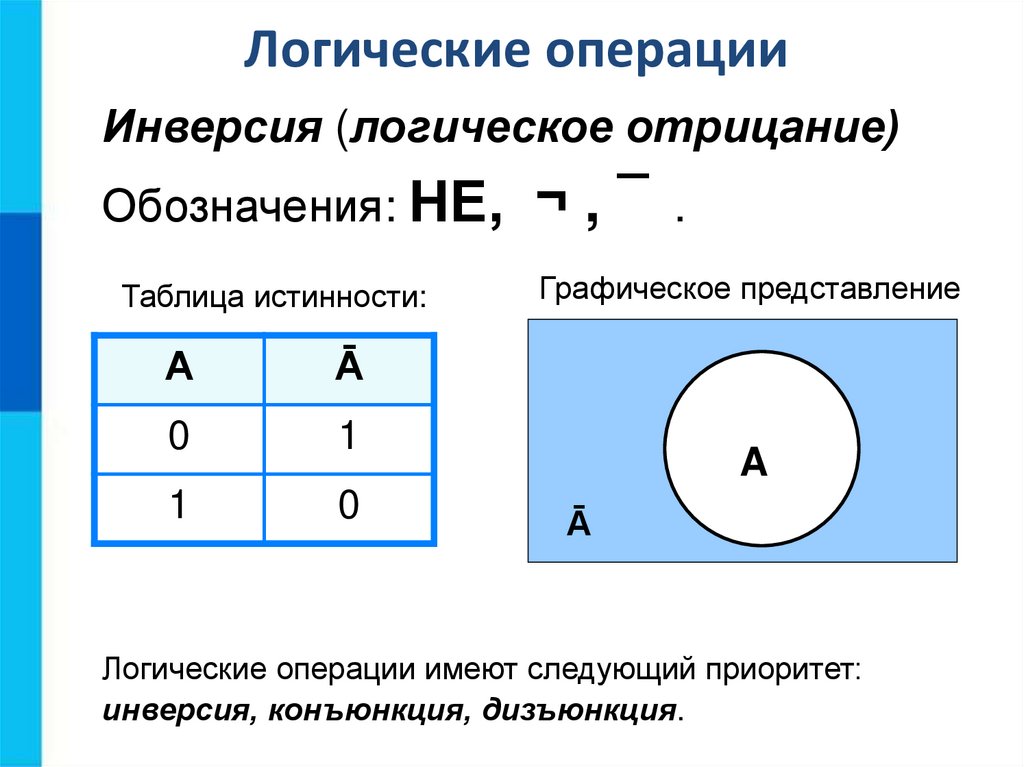
Логические операцииИнверсия (логическое отрицание)
Обозначения: НЕ, ¬ , ¯ .
Таблица истинности:
А
Ā
0
1
1
0
Графическое представление
A
Ā
Логические операции имеют следующий приоритет:
инверсия, конъюнкция, дизъюнкция.
9.
Логической функцией называют функциюF(X1,X2,…Xn), аргументы которой логические
переменные, а сама функция принимает значения либо
0, либо 1.
Таблицу, показывающую,
какие значения принимает
логическая функция при всех
сочетаниях значений её
аргументов называют
таблицей истинности.
10.
Таблицы истинности:n
Количество строк = 2 ,
где N – кол-во логических переменных
Кол-во столбцов =
Кол-во переменных+ Колво логических операций
11.
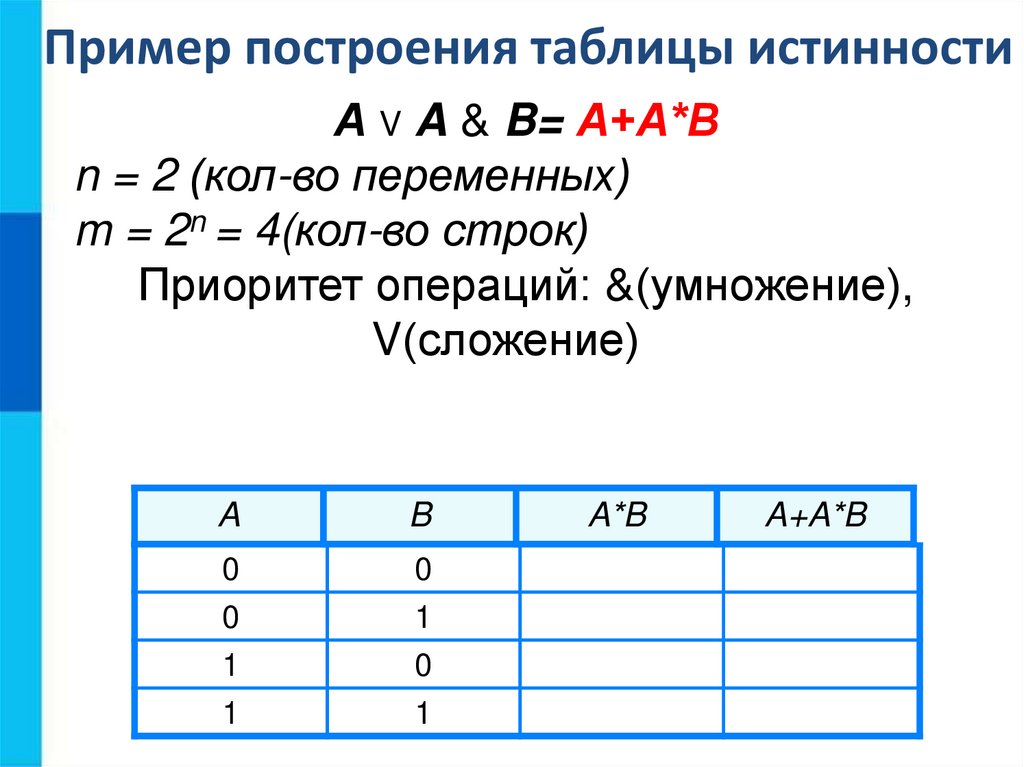
Пример построения таблицы истинностиА V A & B= А+А*В
n = 2 (кол-во переменных)
m = 2n = 4(кол-во строк)
Приоритет операций: &(умножение),
V(сложение)
A
B
0
0
0
1
1
0
1
1
A*B
A+A*B
12.
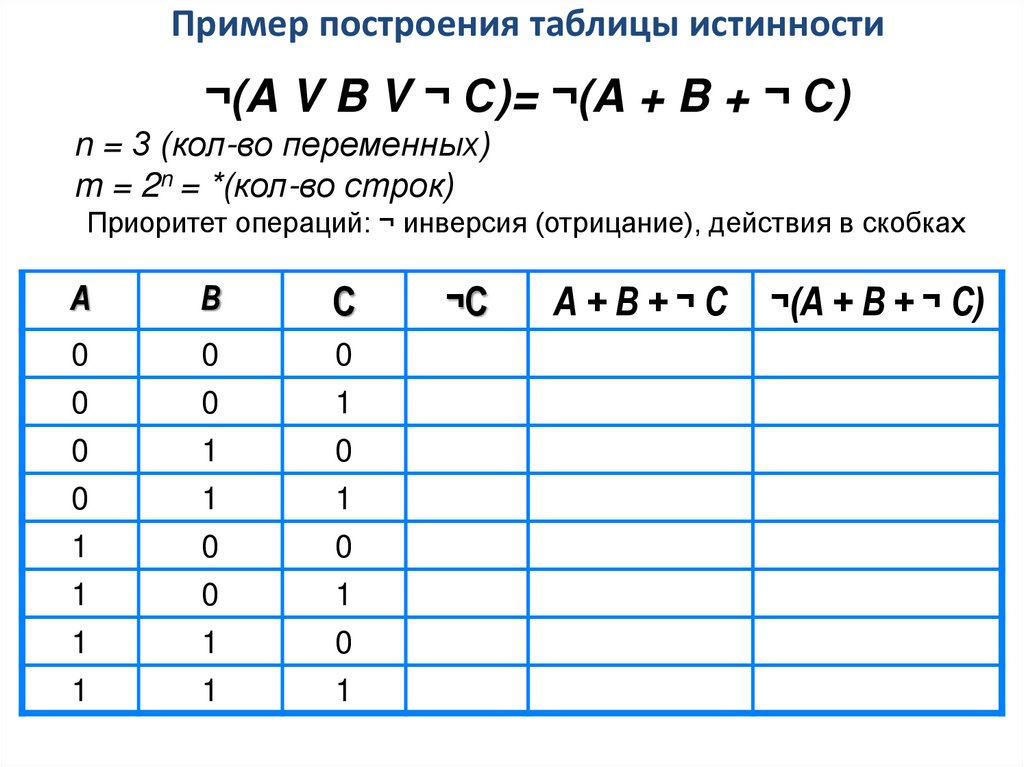
Пример построения таблицы истинности¬(A V B V ¬ С)= ¬(A + B + ¬ С)
n = 3 (кол-во переменных)
m = 2n = *(кол-во строк)
Приоритет операций: ¬ инверсия (отрицание), действия в скобках
A
B
С
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
¬С
A+B+¬С
¬(A + B + ¬ С)
13.
Самостоятельная работаA & (BV¬B)= A * (B+¬B)
n = 2 (кол-во переменных)
m = 2n = 4(кол-во строк)
Приоритет операций: ¬ инверсия
(отрицание), действия в скобках,
умножение
A
B
¬B
B+¬B
А*(В + ¬B)
14.
Самостоятельная работа:Построить таблицу истинности для выражения
А&(AVBVC)=A*(A+B+C)
15.
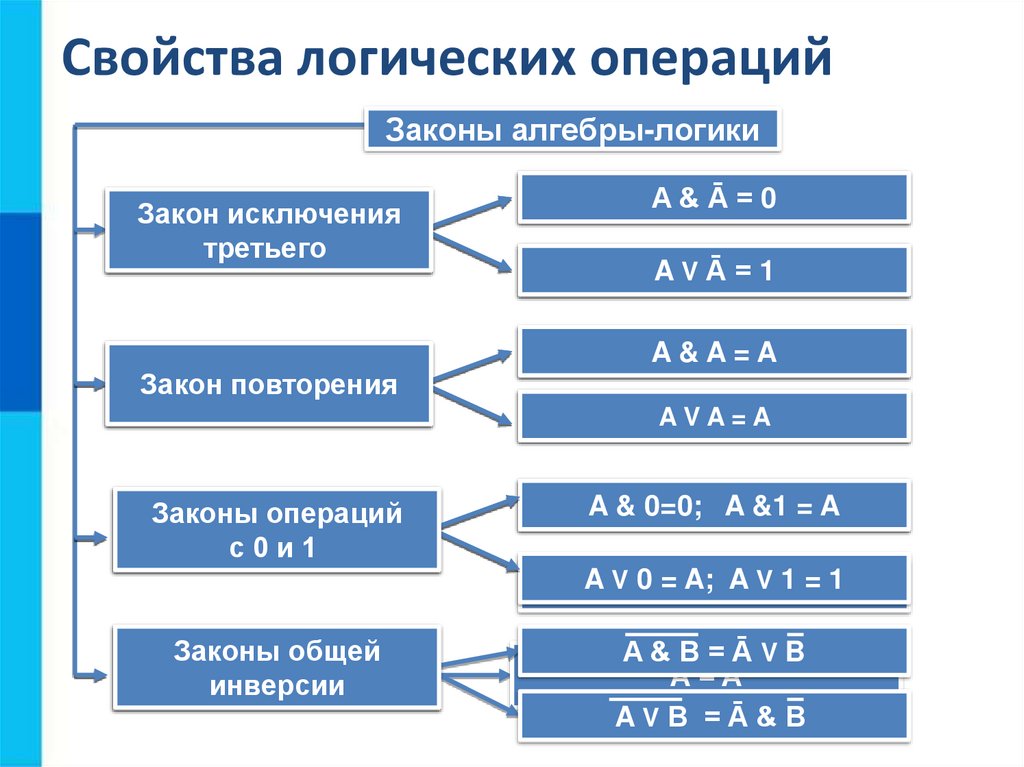
Свойства логических операцийЗаконы алгебры-логики
Закон исключения
Переместительный
третьего
A&
AB
&=
ĀB
=&
0A
AV
AB
VĀ
=B
=V
1A
(A & B) &
AC
& =AA= &
A ( B & C)
Закон
Сочетательный
повторения
(A V B) V
AC
VA
=A=VA( B V C)
Законы операций
Распределительный
с0и1
A&(B
A&
VC)=
0=0;(A&B)
A &1V =(A&C)
A
V 0 ==A;(AA
V1=1
AVA
(B&C)
VB)&(A
VC)
Закон
Законы
двойного
общей
отрицания
инверсии
A&B=ĀVB
Ā=A
AVB =Ā&B








 informatics
informatics