711b3c1f-53ac-4d8f-8334-176dd0c72cc1

1.

Введение в
математические секанс
и косеканс в
профессиональной
деятельности
Секанс и косеканс — обратные функции
косинуса и синуса, важные в инженерии и
науке.
Сергеев Олег 1АС1

2.

История и основы
тригонометрических
функций
Понятия секанса и косеканса возникли из
тригонометрии, применялись в навигации и
строительстве, сегодня они критически важны в
аналитической геометрии и прикладной
математике.
2

3.

Основные свойства секанса и косеканса
Определение функций секанс и
косеканс
Область определения и
графические особенности
Секанс определяется как обратная
величина косинуса: sec(θ)=1/cos(θ), а
косеканс — как 1/sin(θ). Эти функции
расширяют возможности
тригонометрии для разных задач.
Секанс не определён при cos(θ)=0,
косеканс — при sin(θ)=0. Это
приводит к характерным разрывам на
графиках функций, важным для
анализа и вычислений.
Связь с другими
тригонометрическими
функциями
Секанс и косеканс тесно связаны с
синусом, косинусом и тангенсом, что
позволяет использовать тождества и
упрощать сложные вычисления в
прикладных областях.
3

4.

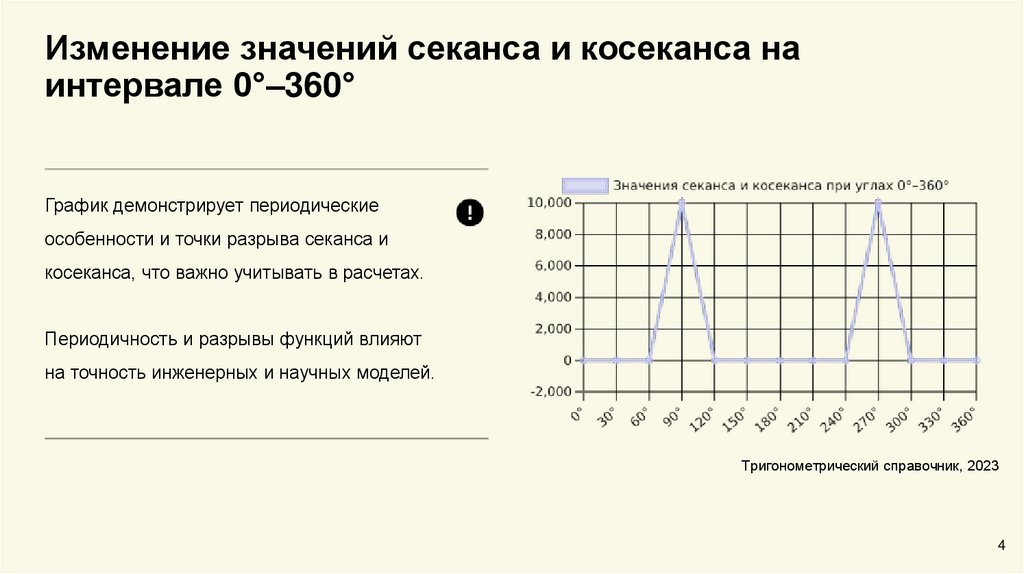
Изменение значений секанса и косеканса на
интервале 0°–360°
График демонстрирует периодические
особенности и точки разрыва секанса и
косеканса, что важно учитывать в расчетах.
Периодичность и разрывы функций влияют
на точность инженерных и научных моделей.
Тригонометрический справочник, 2023
4

5.

Применение секанса и косеканса в инженерных
расчетах
Примеры расчетов высот, сил и углов с
использованием секанса и косеканса демонстрируют
их практическую эффективность.
Тригонометрические функции упрощают и повышают
надежность инженерных вычислений.
Инженерный справочник, 2022
5

6.

Секанс и косеканс в компьютерном моделировании и программировании
Используются для расчёта
ориентации и трансформации
объектов в 3D-пространстве,
обеспечивая точность
позиционирования.
В машинном зрении и
робототехнике помогают оценить
углы наклона и положение,
повышая качество обработки
данных.
Также обеспечивают устойчивость
вычислений в численных методах
при близких к точкам разрыва
углах.
6

7.

Использование секанса и косеканса в физике и метрологии
Решение задач механики
Оптические измерения
Анализ волн и сигналов
Функции секанса и косеканса
применяются для определения сил и
углов в динамике, облегчая расчеты
сложных физических систем.
Измерение углов отражения и
преломления света основано на
тригонометрических расчетах с
использованием косеканса и секанса
для точного контроля процессов.
Угловые зависимости интенсивности
сигналов и взаимодействия волн
исследуются через данные функции,
что важно для метрологических
приборов.
7

8.

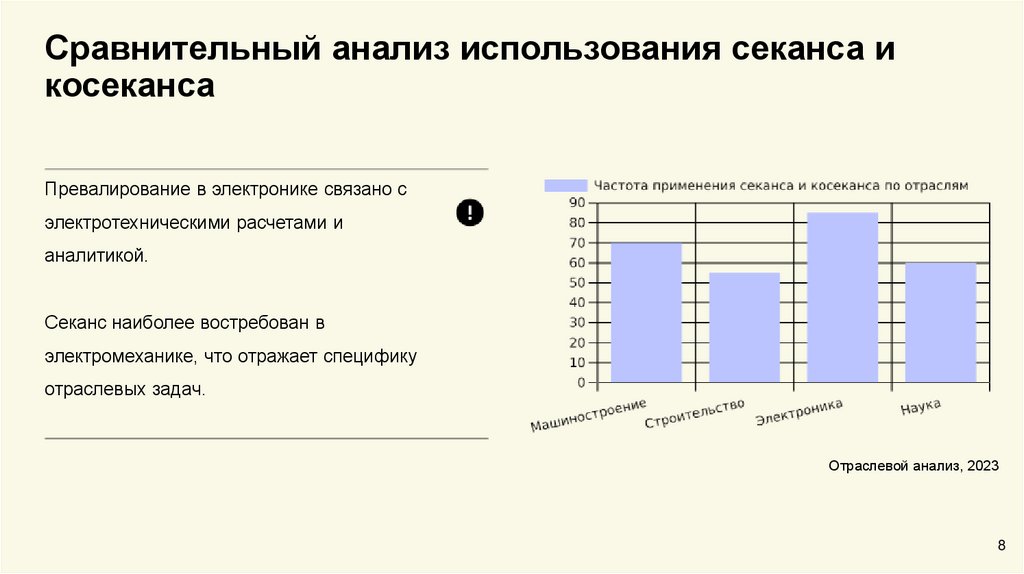
Сравнительный анализ использования секанса и
косеканса
Превалирование в электронике связано с
электротехническими расчетами и
аналитикой.
Секанс наиболее востребован в
электромеханике, что отражает специфику
отраслевых задач.
Отраслевой анализ, 2023
8

9.

Ограничения и трудности при работе с секансом и косекансом
Точки разрыва функций (90°, 270° и др.) требуют
особой внимательности, чтобы избежать деления
на ноль в вычислениях.
При численных методах следует применять
приближенные значения, чтобы минимизировать
ошибки и нестабильность результатов.
Недостоверное обращение с особенностями
функций может привести к некорректным итогам
в инженерных и научных расчетах.
Рекомендуется использовать
специализированные библиотеки и алгоритмы с
учётом всех нулевых значений синуса и
косинуса.
9

10.

Значимость секанса и косеканса в
профессиональных расчетах
Глубокое понимание секанса и косеканса критично для точности инженерных и научных
решений во множестве дисциплин и технологий.