Дәріс№10-11.Граф

1. Графтар теориясы

2. Графтарды беру тәсілі

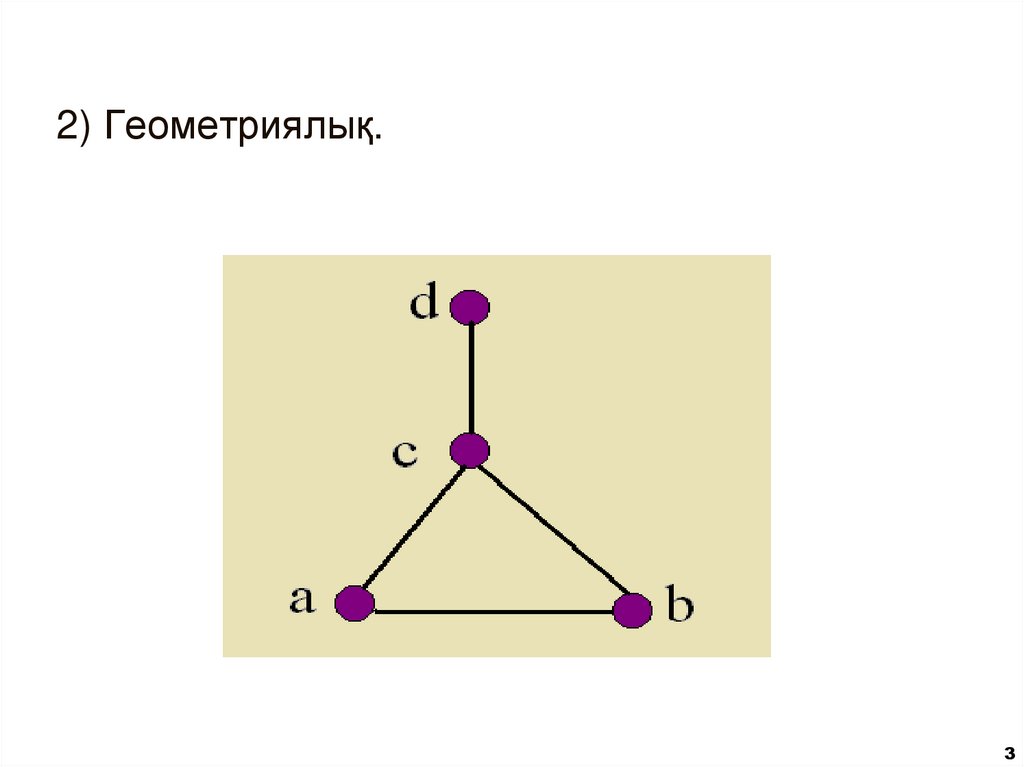
1)
{{a,b},{b,c},{a,c},{c,d}}
2

3.

2) Геометриялық.
3

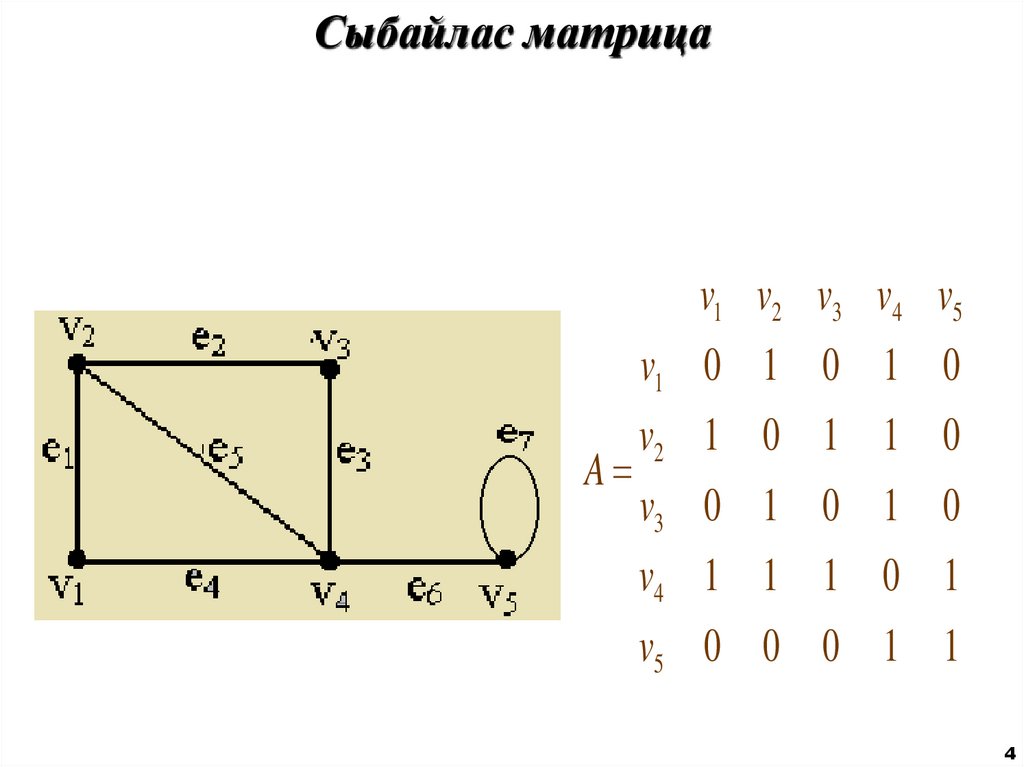
4. Сыбайлас матрица

v1
v2
A
v3
v4
v5
v1
0
1
0
1
0
v2
1
0
1
1
0
v3
0
1
0
1
0
v4
1
1
1
0
1
v5
0
0
0
1
1
4

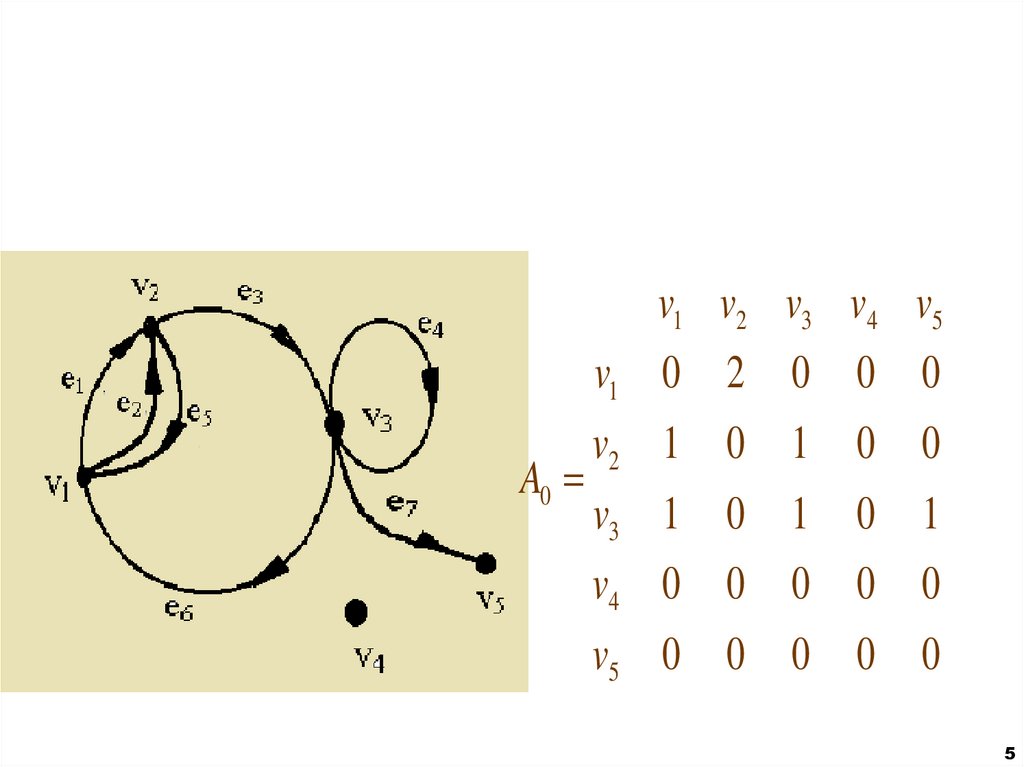
5.

v1
v2
A0
v3
v4
v5
v1
0
1
1
0
0
v2
2
0
0
0
0
v3
0
1
1
0
0
v4
0
0
0
0
0
v5
0
0
1
0
0
5

6.

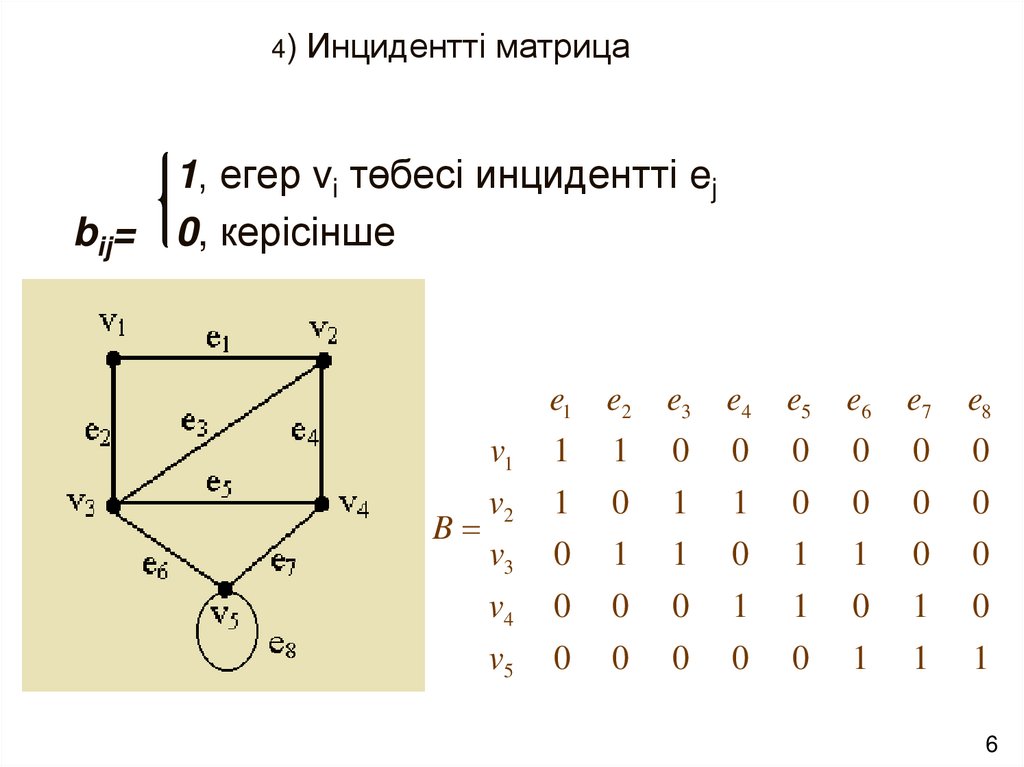
4) Инцидентті матрица
bij=
1, егер vi төбесі инцидентті ej
0, керісінше
v1
v2
B
v3
v4
v5
e1 e2
1 1
1 0
0 1
0 0
0 0
e3
0
1
1
0
0
e4
0
1
0
1
0
e5
0
0
1
1
0
e6
0
0
1
0
1
e7
0
0
0
1
1
e8
0
0
0
0
1
6

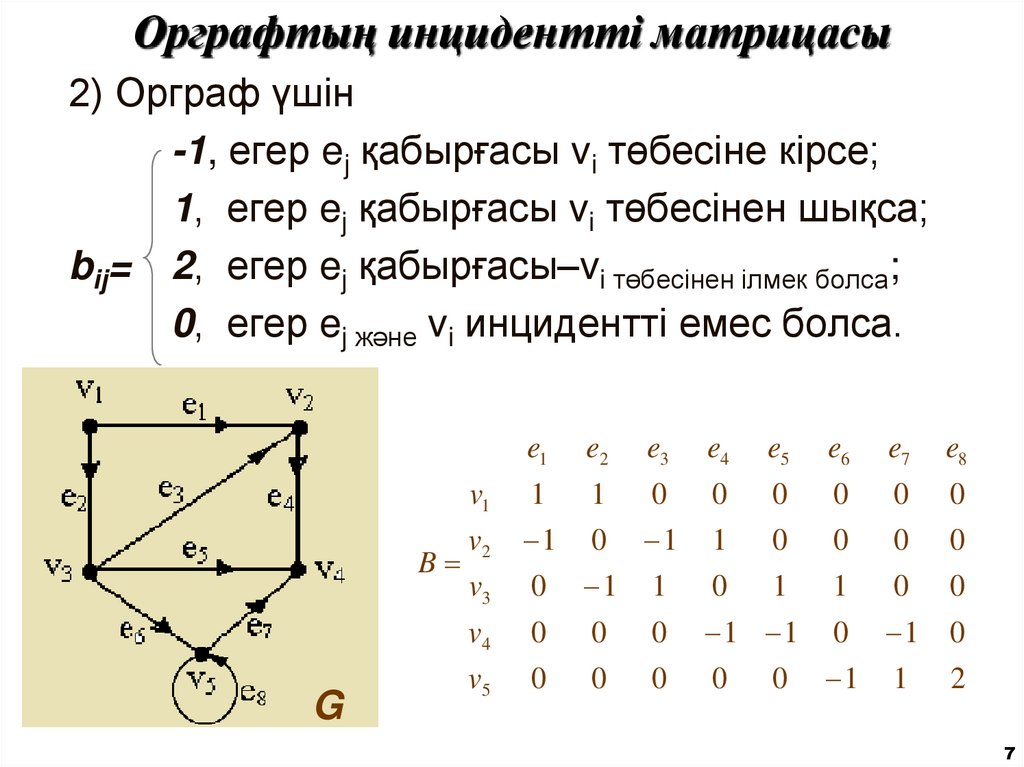
7. Орграфтың инцидентті матрицасы

2) Орграф үшін
-1, егер ej қабырғасы vi төбесіне кірсе;
1, егер ej қабырғасы vi төбесінен шықса;
bij= 2, егер ej қабырғасы–vi төбесінен ілмек болса;
0, егер ej және vi инцидентті емес болса.
G
v1
v2
B
v3
v4
v5
e1 e2 e3 e4 e5 e6 e7
1 1 0 0 0 0 0
1 0 1 1 0 0 0
0 1 1 0 1 1 0
0 0 0 1 1 0 1
0 0 0 0 0 1 1
e8
0
0
0
0
2
7

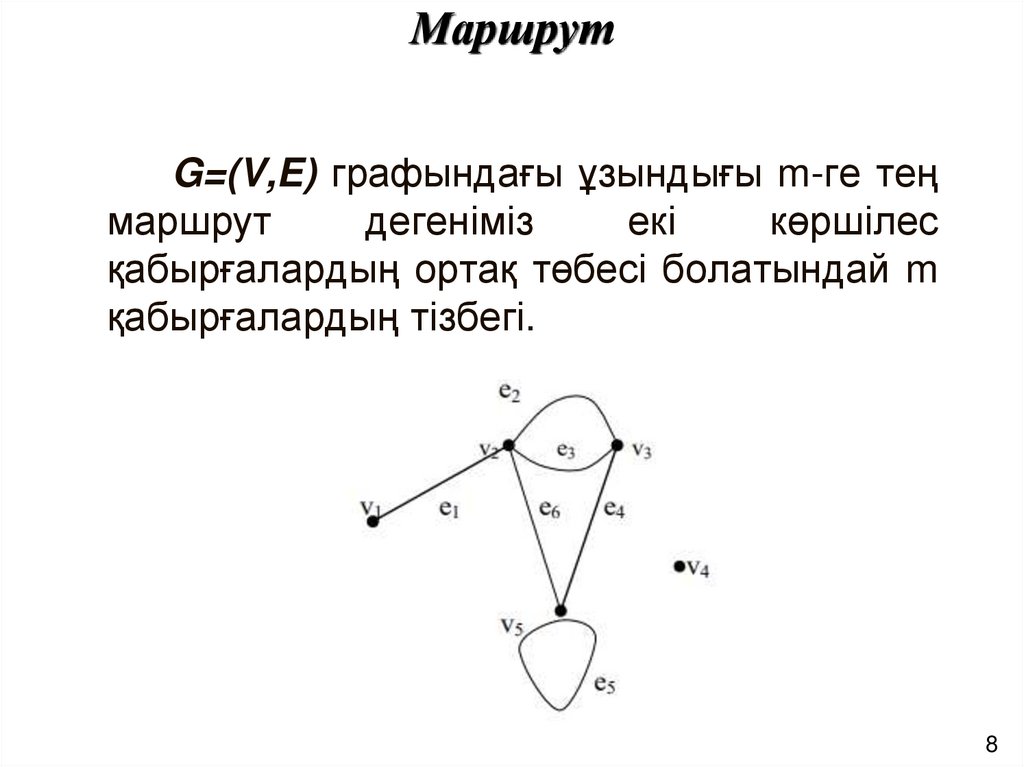
8. Маршрут

G=(V,E) графындағы ұзындығы m-ге тең
маршрут
дегеніміз
екі
көршілес
қабырғалардың ортақ төбесі болатындай m
қабырғалардың тізбегі.
8

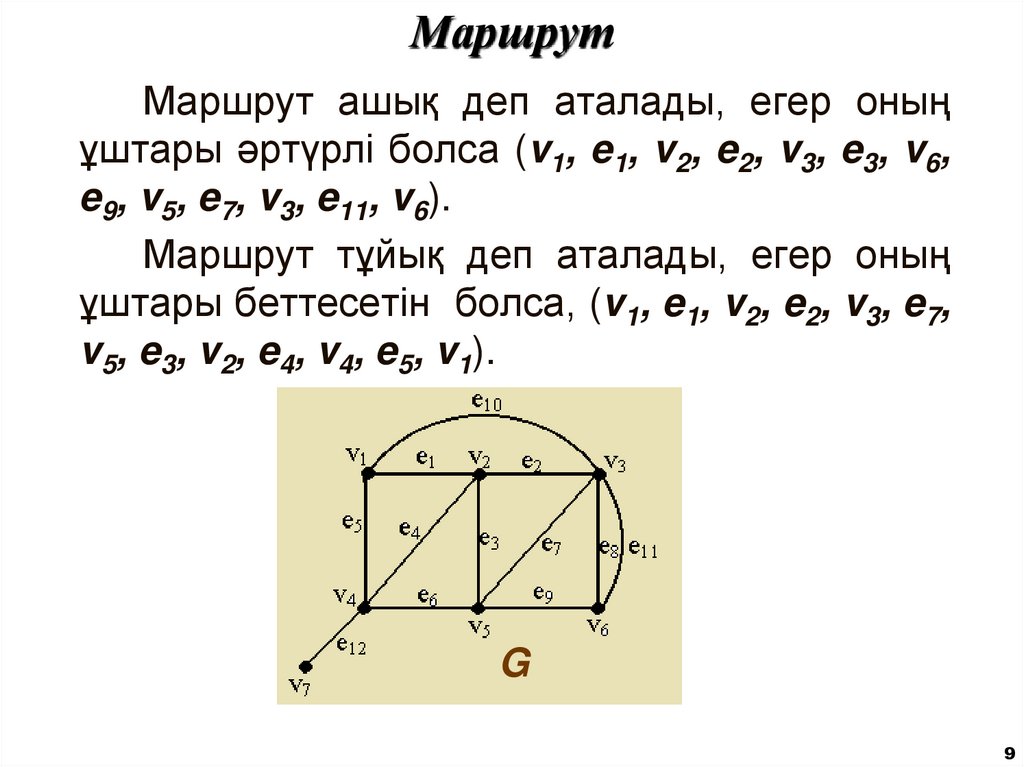
9. Маршрут

Маршрут ашық деп аталады, егер оның
ұштары әртүрлі болса (v1, e1, v2, e2, v3, e3, v6,
e9, v5, e7, v3, e11, v6).
Маршрут тұйық деп аталады, егер оның
ұштары беттесетін болса, (v1, e1, v2, e2, v3, e7,
v5, e3, v2, e4, v4, e5, v1).
G
9

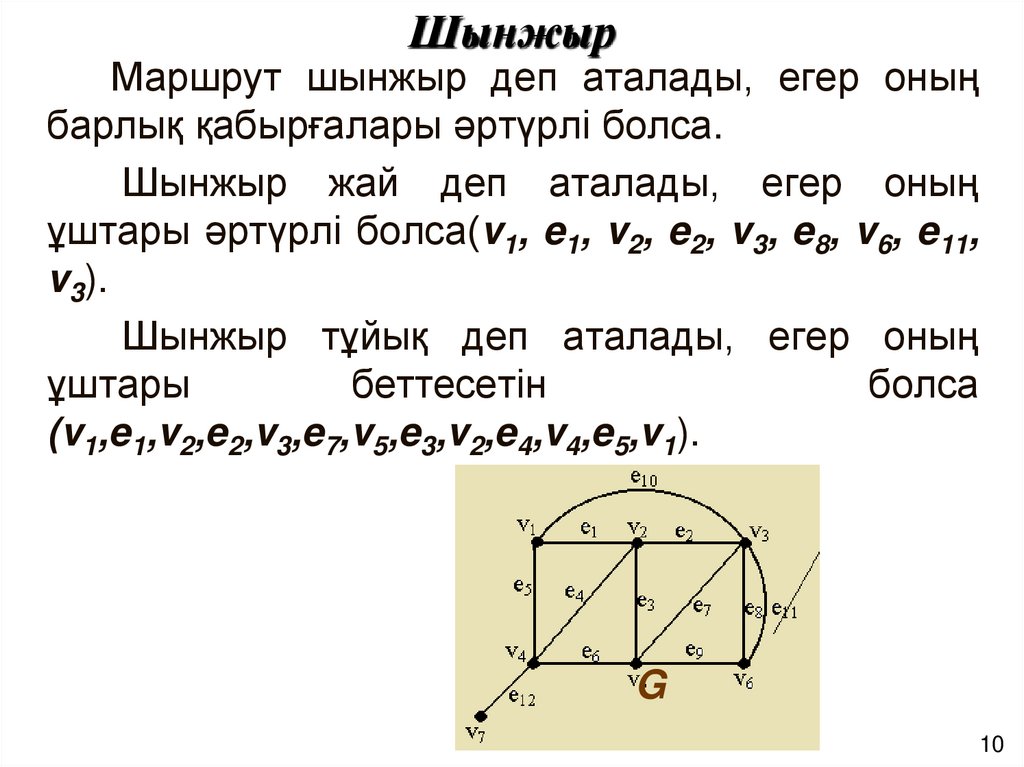
10. Шынжыр

Маршрут шынжыр деп аталады, егер оның
барлық қабырғалары әртүрлі болса.
Шынжыр жай деп аталады, егер оның
ұштары әртүрлі болса(v1, e1, v2, e2, v3, e8, v6, e11,
v3).
Шынжыр тұйық деп аталады, егер оның
ұштары
беттесетін
болса
(v1,e1,v2,e2,v3,e7,v5,e3,v2,e4,v4,e5,v1).
G
10

11. Жол, цикл

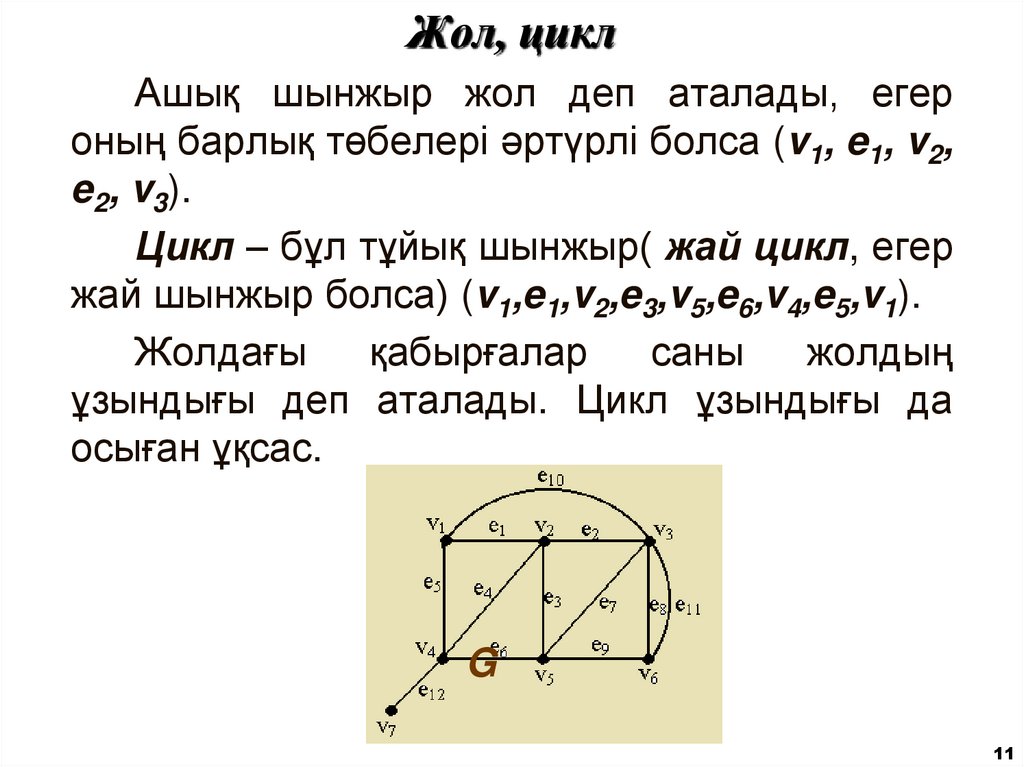
Ашық шынжыр жол деп аталады, егер
оның барлық төбелері әртүрлі болса (v1, e1, v2,
e2, v3).
Цикл – бұл тұйық шынжыр( жай цикл, егер
жай шынжыр болса) (v1,e1,v2,e3,v5,e6,v4,e5,v1).
Жолдағы
қабырғалар
саны
жолдың
ұзындығы деп аталады. Цикл ұзындығы да
осыған ұқсас.
G
11

12. Жолдар мен циклдердің қасиеттері

1.
Жолдың әрбір ұшы емес төбелерінің
көрсеткіші 2-ге тең, ал ұшы болатын төбелер
көрсеткіші 1-ге тең.
2. Циклдің әрбір төбесінің көрсеткіші 2-ге тең
немесе басқа жұп көрсеткішке ие.
3. Жолдағы төбелер саны қабырғалар санынан
бірге артық
12

13. Графтардың байланыстылығы, байланыс компоненті

G графындағы vi және vj екі төбесі
байланысқан деп аталады, егер онда vi—vj жол
болса.
Граф байланысқан деп аталады, егер онда
әрбір жұп төбелері арасындағы жол болса.
Байланыс компоненті
– графтағы
максимальды байланысқан ішкі граф
1 байланыс компоненті: {v1, v2, v3, e1, e2, e3}
2 байланыс компоненті : {v4, v5, v6, e4, e5, e6}
3 байланыс компоненті : {v7, v8, e7}
4 байланыс компоненті : {v9}
G
13

14. Изоморфизм

Екі граф G1 және G2 изоморфты деп
аталады, егер G1 және G2 графтарының сәйкес
қабырғалары сәйкес төбелеріне инцидентті
болатындай,
олардың
төбелері
мен
қабырғалары жиындары арасында өзара
бірмәнді бейнелеу болса.
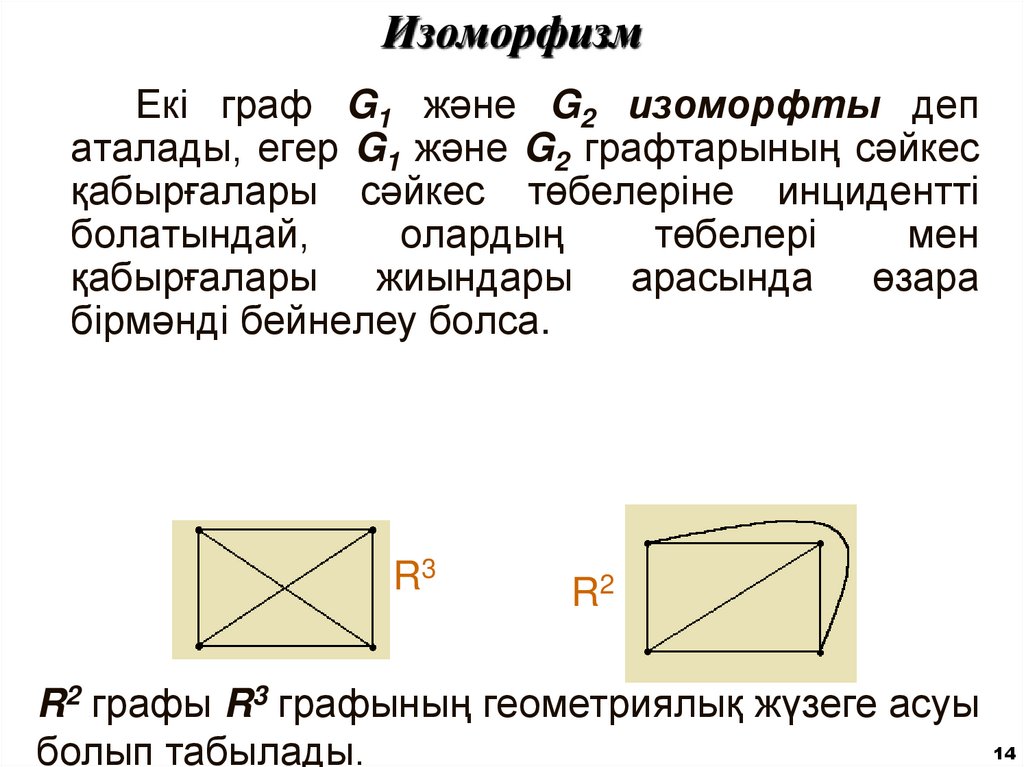
R3
R2
R2 графы R3 графының геометриялық жүзеге асуы
14
болып табылады.

15. Изоморфты графтар мысалы

Төбелер сәйкестігі:
v1 v2’,v2 v3’,v3 v1’,v4 v4’,v5 v5’;
Қабырғалар сәйкестігі:
e1 e1’, e3 e2’, e5 e4’, e2 e5’, e4 e6’, e6 e3’.
G1
G2
G1 және G2 – изоморфты графтар
15