Дәріс№9 граф

1. Графтар теориясы

2.

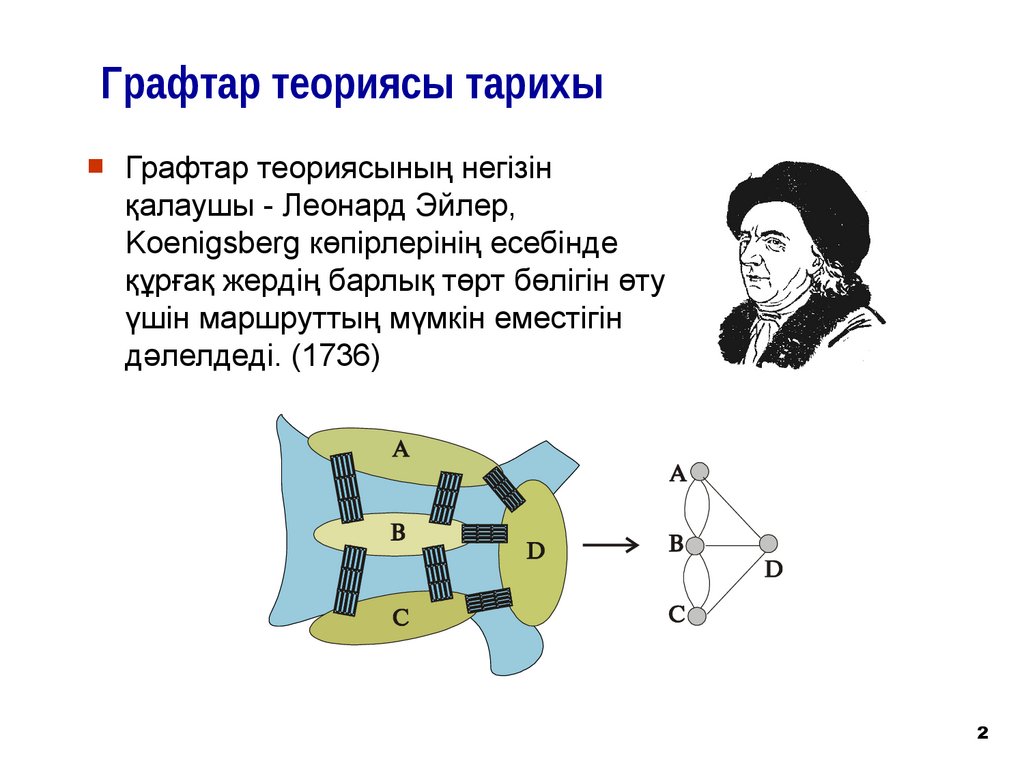
Графтар теориясы тарихы
Графтар теориясының негізін
қалаушы - Леонард Эйлер,
Koenigsberg көпірлерінің есебінде
құрғақ жердің барлық төрт бөлігін өту
үшін маршруттың мүмкін еместігін
дәлелдеді. (1736)
2

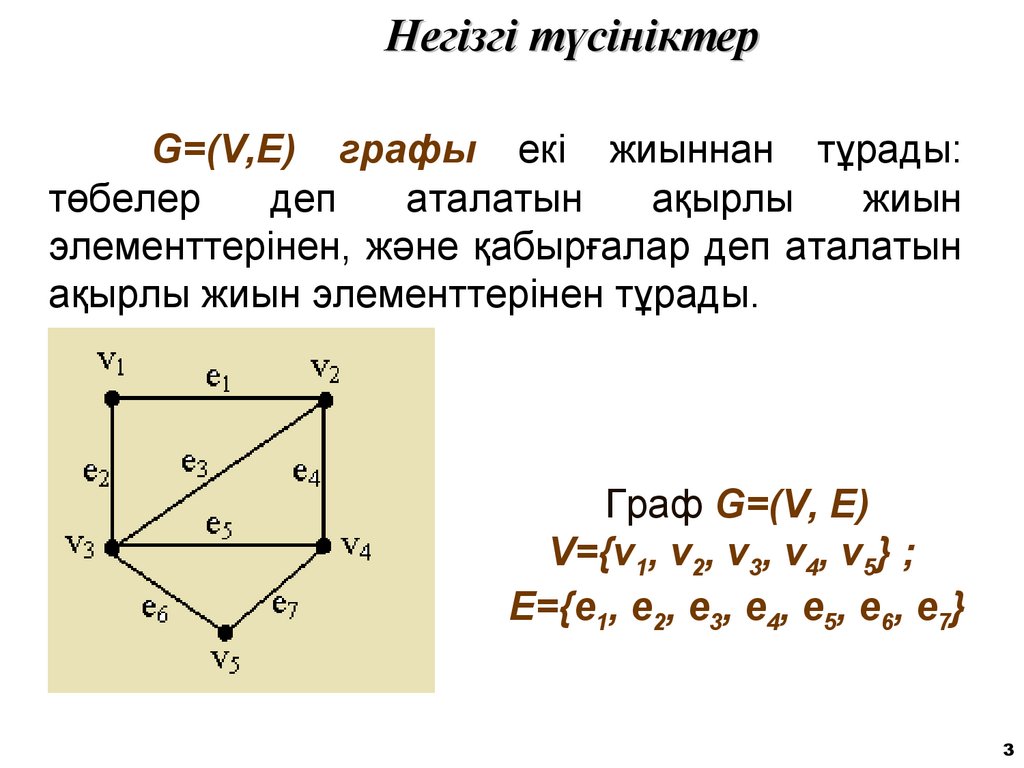
3. Негізгі түсініктер

G=(V,E) графы екі жиыннан тұрады:
төбелер
деп
аталатын
ақырлы
жиын
элементтерінен, және қабырғалар деп аталатын
ақырлы жиын элементтерінен тұрады.
Граф G=(V, E)
V={v1, v2, v3, v4, v5} ;
E={e1, e2, e3, e4, e5, e6, e7}
3

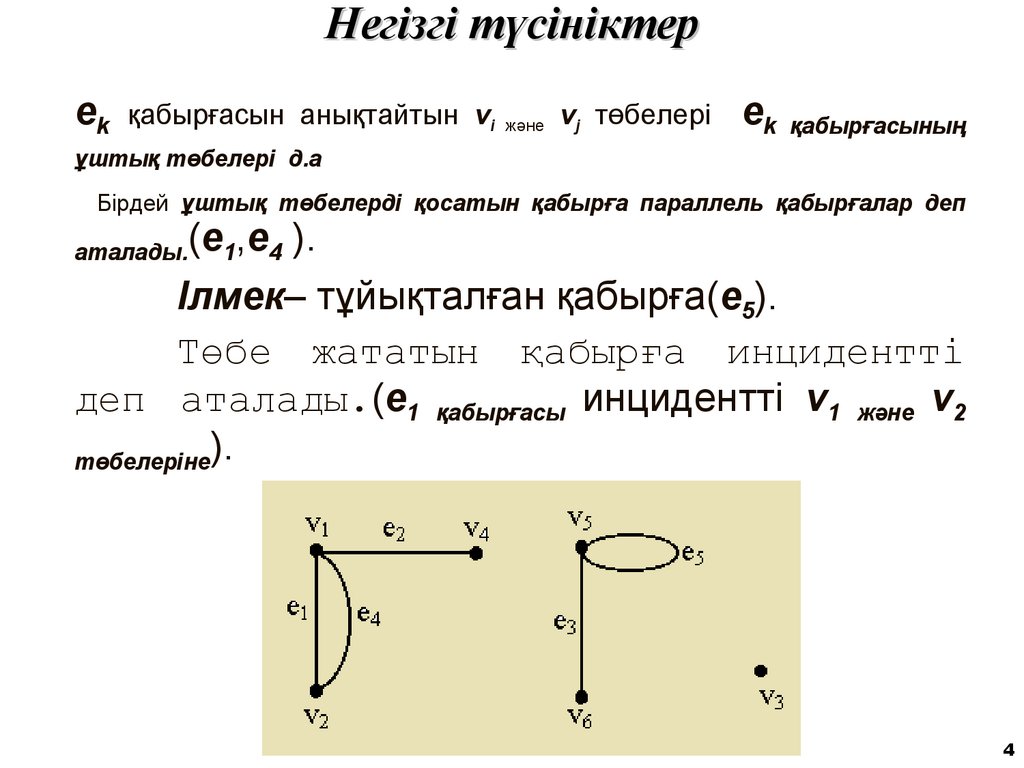
4. Негізгі түсініктер

ek қабырғасын анықтайтын vi және vj төбелері ek қабырғасының
ұштық төбелері д.а
Бірдей ұштық төбелерді қосатын қабырға параллель қабырғалар деп
(e1,e4 ).
Ілмек– тұйықталған қабырға(e5).
Төбе жататын қабырға инцидентті
деп аталады.(e1 қабырғасы инцидентті v1 және v2
төбелеріне).
аталады.
4

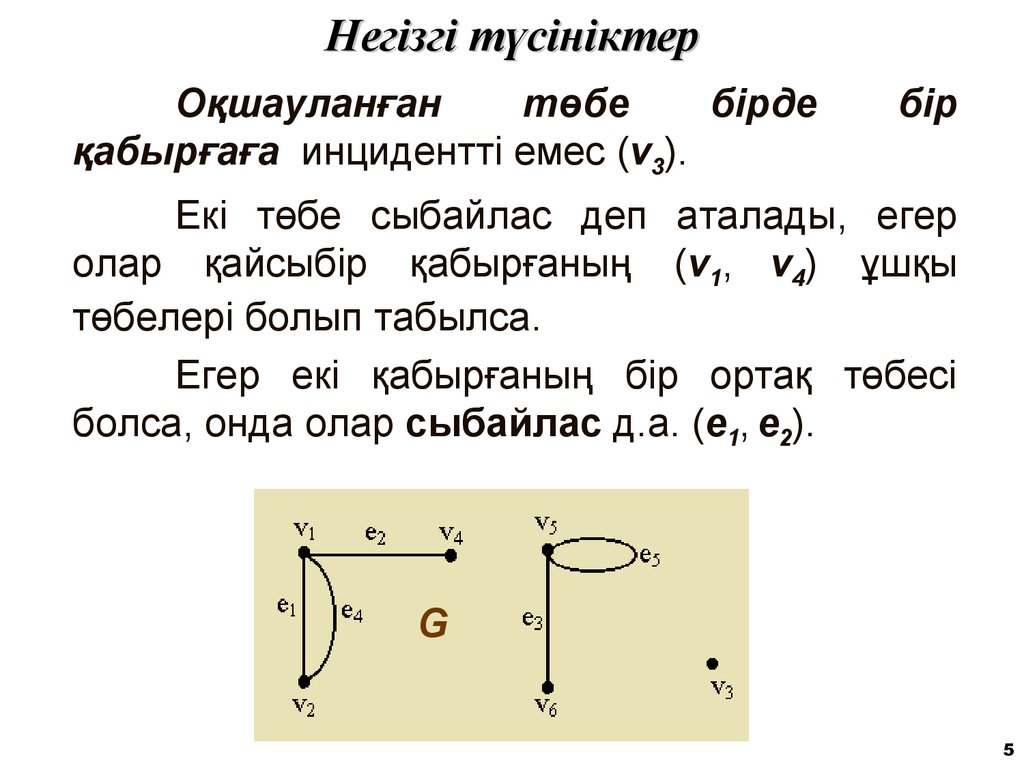
5. Негізгі түсініктер

Оқшауланған
төбе
бірде
қабырғаға инцидентті емес (v3).
бір
Екі төбе сыбайлас деп аталады, егер
олар қайсыбір қабырғаның (v1, v4) ұшқы
төбелері болып табылса.
Егер екі қабырғаның бір ортақ төбесі
болса, онда олар сыбайлас д.а. (e1, e2).
G
5

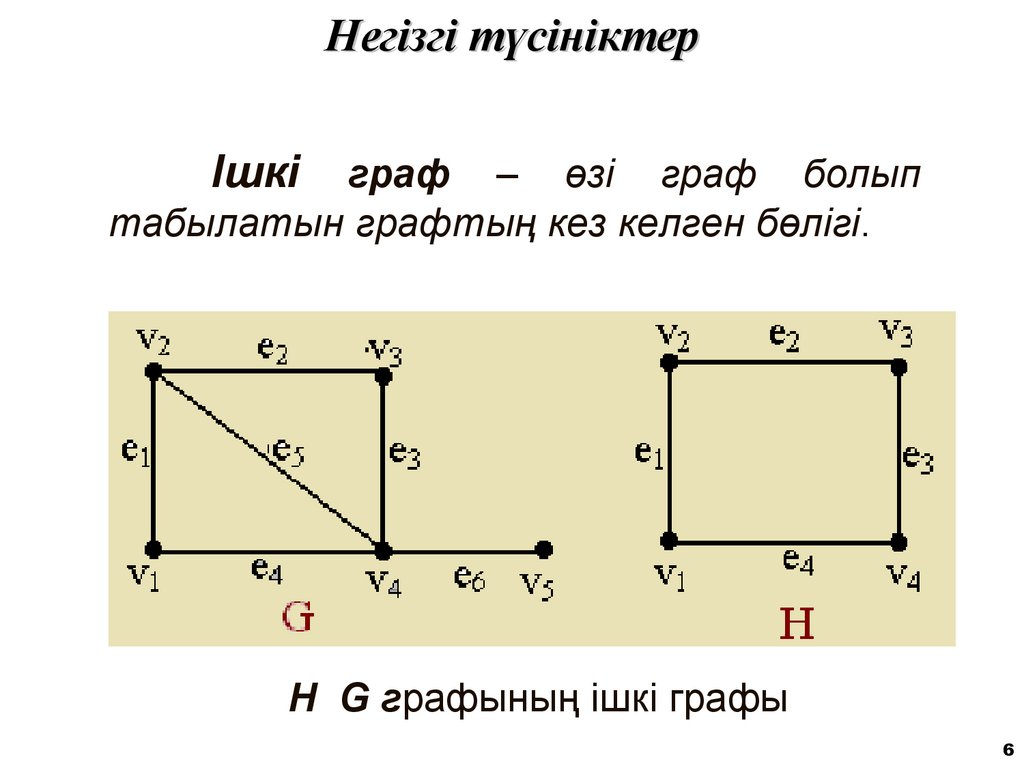
6. Негізгі түсініктер

Ішкі
граф – өзі граф болып
табылатын графтың кез келген бөлігі.
H G графының ішкі графы
6

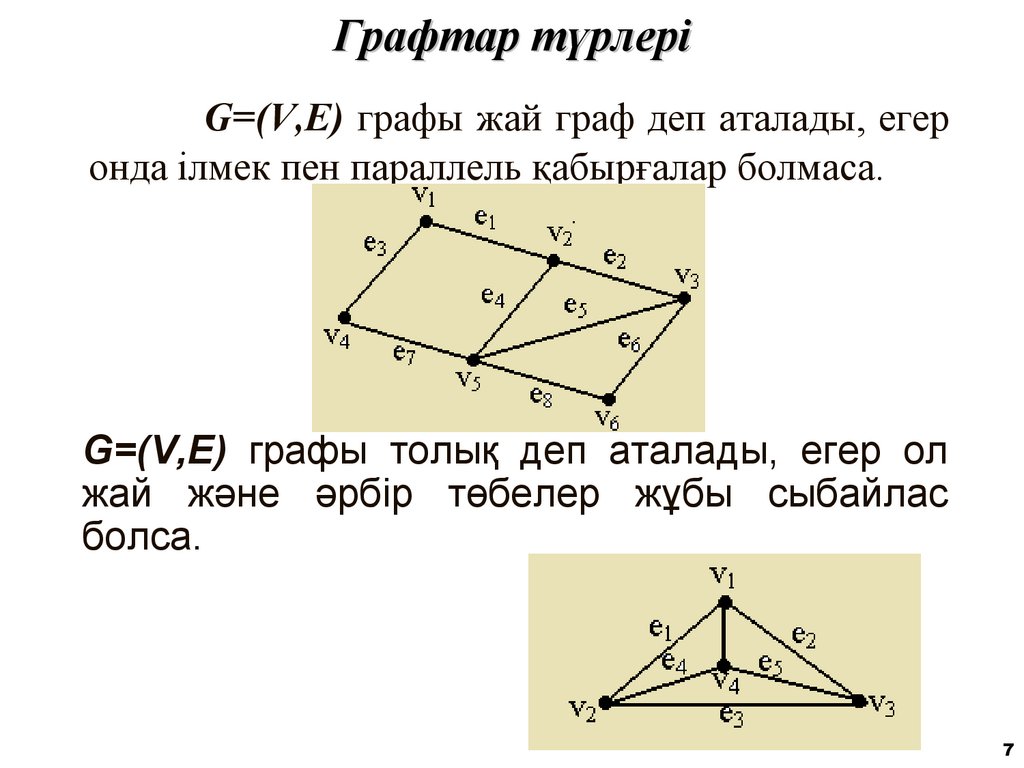
7. Графтар түрлері

G=(V,E) графы жай граф деп аталады, егер
онда ілмек пен параллель қабырғалар болмаса.
G=(V,E) графы толық деп аталады, егер ол
жай және әрбір төбелер жұбы сыбайлас
болса.
7

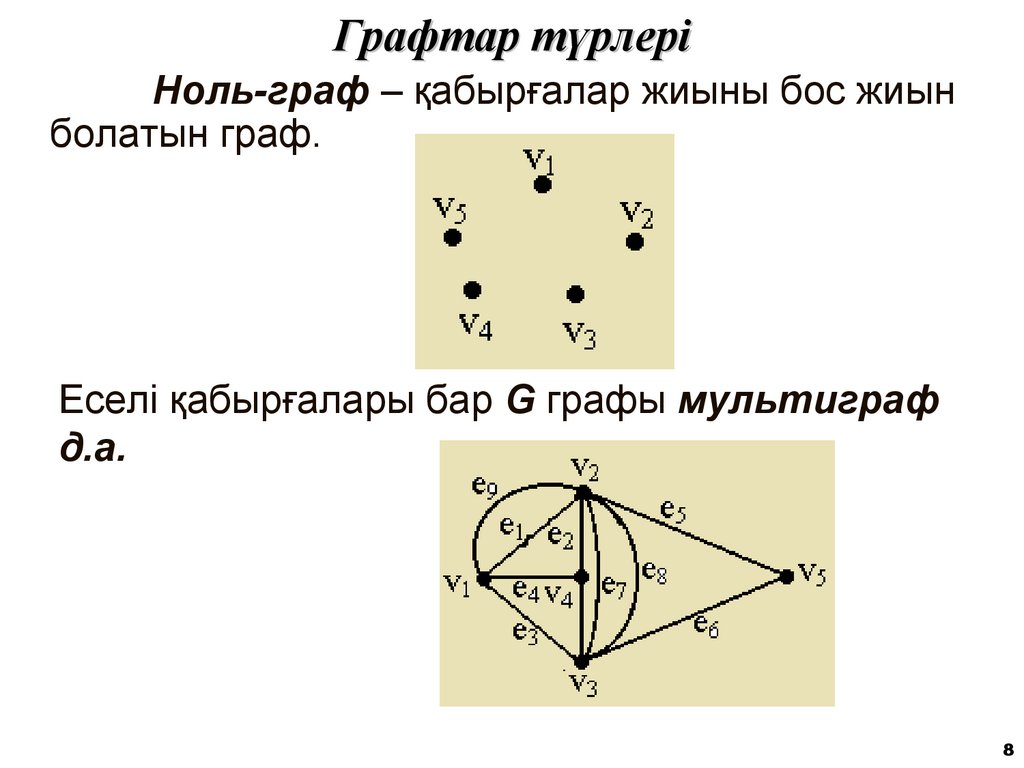
8. Графтар түрлері

Ноль-граф – қабырғалар жиыны бос жиын
болатын граф.
Еселі қабырғалары бар G графы мультиграф
д.а.
8

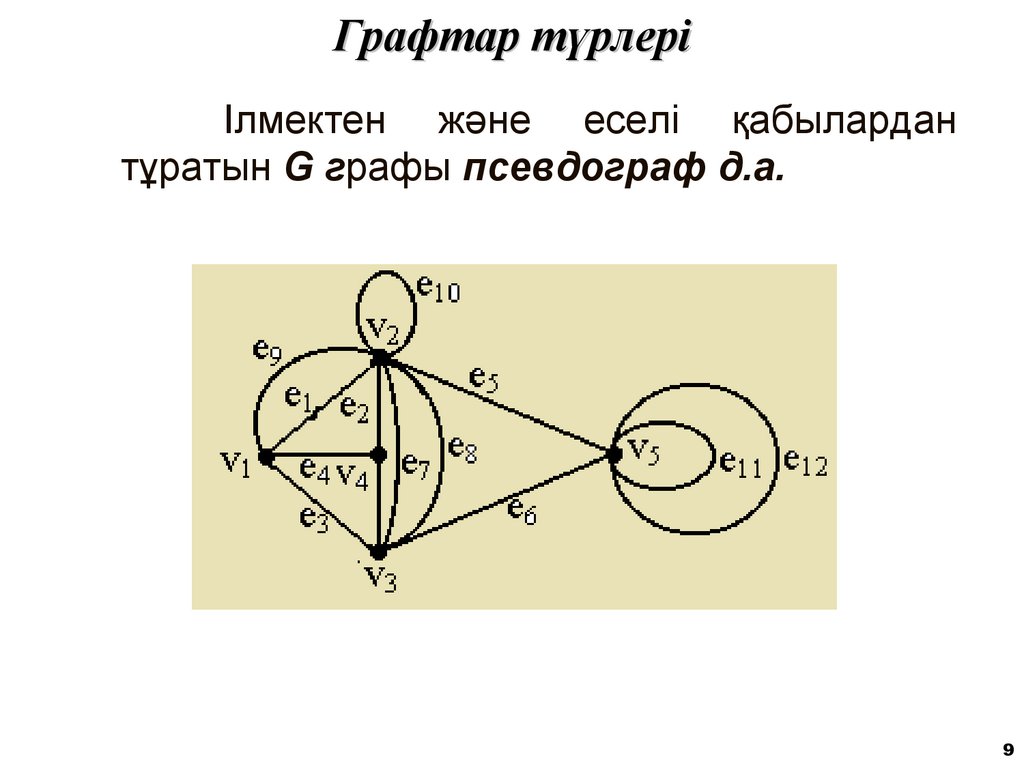
9. Графтар түрлері

Ілмектен және еселі қабылардан
тұратын G графы псевдограф д.а.
9

10.

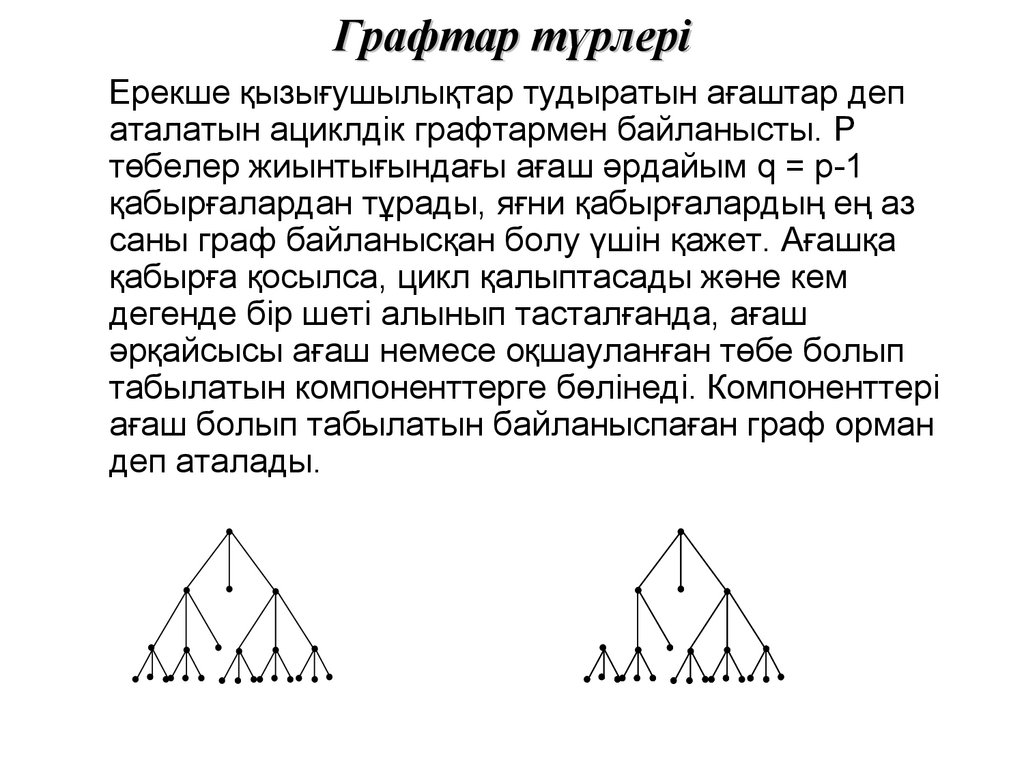
Графтар түрлері
Ерекше қызығушылықтар тудыратын ағаштар деп
аталатын ациклдік графтармен байланысты. P
төбелер жиынтығындағы ағаш әрдайым q = p-1
қабырғалардан тұрады, яғни қабырғалардың ең аз
саны граф байланысқан болу үшін қажет. Ағашқа
қабырға қосылса, цикл қалыптасады және кем
дегенде бір шеті алынып тасталғанда, ағаш
әрқайсысы ағаш немесе оқшауланған төбе болып
табылатын компоненттерге бөлінеді. Компоненттері
ағаш болып табылатын байланыспаған граф орман
деп аталады.

11.

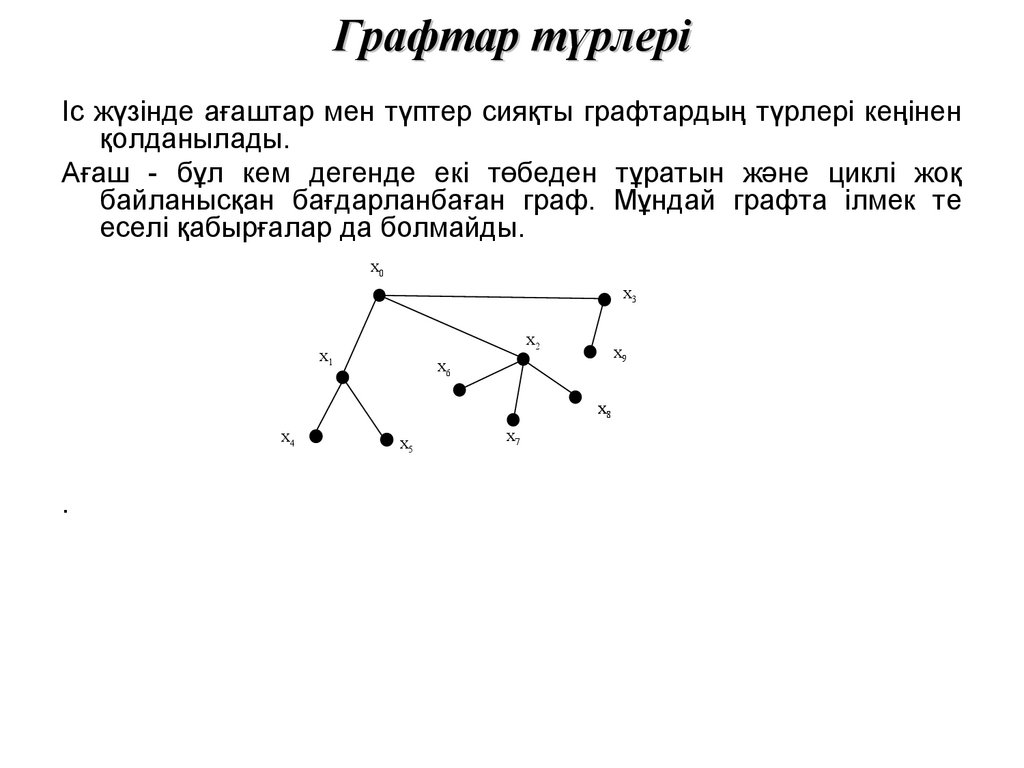
Графтар түрлері
Іс жүзінде ағаштар мен түптер сияқты графтардың түрлері кеңінен
қолданылады.
Ағаш - бұл кем дегенде екі төбеден тұратын және циклі жоқ
байланысқан бағдарланбаған граф. Мұндай графта ілмек те
еселі қабырғалар да болмайды.
х0
х3
х2
х1
х9
х6
х8
х4
.
х5
х7