Практикум_7_формулы_17.10.2023

1. Практикум №7 Вычислительная математика

Санкт-Петербургский политехнический университет Петра Великого
Практикум №7
Вычислительная математика
Воскобойников С.П.
Доцент ВШ ПИ ИКНТ, к.ф.-м.н.
voskob_sp@spbstu.ru
17.10.2023

2. Содержание

• Разделённые разности. Таблица
разделённых разностей.
• Интерполяционный полином Ньютона.
• Пример.
• Сходимость интерполяционного
процесса.

3. Разделённые разности и их свойства

xk , f xk , k 0,1,..., n
hk xk xk 1
f xk 1 , xk
f xk 1 , xk , xk 1
f x0 , x1 ,..., xn 1 , xn
f xk 1 , xk , xk 1
k 1,2,..., n
f xk , xk 1 f xk 1 , xk
,
xk 1 xk 1
k 1,2,..., n 1
f x1 ,..., xn 1 , xn f x0 , x1 ,..., xn 1
,
xn x0
f xk 1 , xk
f xk 1 , xk , xk 1
f k f k 1
,
xk xk 1
f k 1
fk
,
xk 1 xk xk xk 1
f k 1 f k f k f k 1
1
,
xk 1 xk 1 xk 1 xk xk xk 1
f k 1
fk
f k 1
,
xk 1 xk xk 1 xk 1 xk xk 1 xk xk 1 xk 1 xk 1 xk 1 xk

4. Разделённые разности и их свойства

f x0 , x1 ,..., xk 1 , xk
f x0
x0 x1 x0 x2 ... x0 xл
...
f x1
...
x1 x0 x1 x2 ... x1 xk
f xk
,
xk x0 xk x1 ... xk xk 1
k
f x0 , x1 ,..., xk 1 , xk k
i 0
f xi
,
x x
i
j
j 0
j i
m k
f xm , xm 1 ,..., xm k 1 , xm k m k
i m
f xi
,
x x
i
j m
j i
j

5. Разделённые разности и их свойства

hk xk xk 1 h,
f xk 1 , xk
f k f k 1 f k
,
xk xk 1
h
f k 2 f k 1 f k 1 f k f k 2 2 f k 1 f k 2 f k
1
f xk , xk 1 , xk 2
,
2
2
xk 2 xk xk 2 xk 1 xk 1 xk
2h
2!h
k fi
f xi , xi 1 ,..., xi k 1 , xi k
,
k
k!h

6. Таблица разделённых разностей

x
f
x0
f0
x1
f1
.
.
xi 1
fi 1
xi
fi
xi 1
.
fi 1
.
xn 1
f n 1
xn
fn
f xi , xi 1
f x0 , x1
f x1, x2
.
f xi 1, xi
f xi , xi 1
f xi , xi 1 ,..., xi n
f xi , xi 1 , xi 2
f x0 , x1, x2
.
…
f xi 1 , xi , xi 1
f x0 , x1 ,..., xn 1 , xn
…
.
f xn 2 , xn 1
f xn 1 , xn
.
f xn 2 , xn 1 , xn

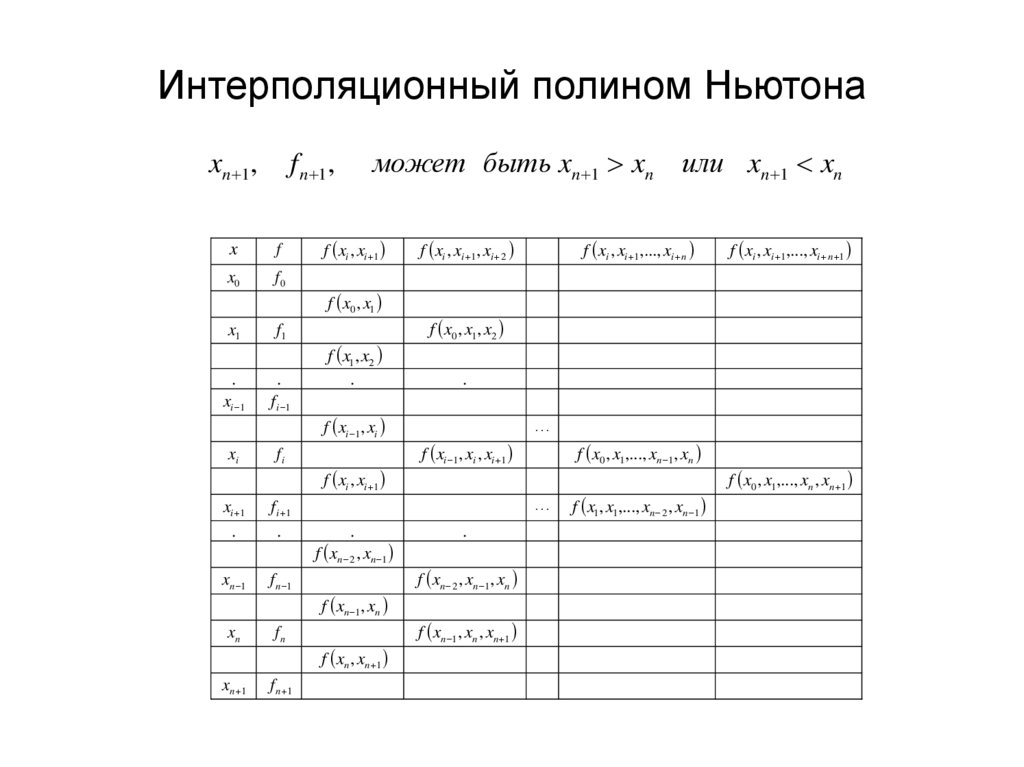
7. Интерполяционный полином Ньютона

Nn x f x0 x x0 f x0 , x1 x x0 x x1 f x0 , x1, x2 ... x x0 x x1 ... x xn 1 f x0 , x1,..., xn ,
n
i 1
N n x f x0 x xk f x0 , x1 ,..., xi ,
i 1 k 0
n 1
N n x N n 1 x x xk f x0 , x1 ,..., xn , N 0 x f x0 , n 1,2,...
k 0
N1 x f x0 x x0 f x0 , x1 ,
N2 x f x0 x x0 f x0 , x1 x x0 x x1 f x0 , x1, x2 ,

8. Интерполяционный полином Ньютона

xn 1 ,
может быть xn 1 xn
f n 1 ,
x
f
x0
f0
x1
f1
.
.
xi 1
fi 1
xi
fi
xi 1
.
fi 1
.
xn 1
f n 1
xn
fn
xn 1
f n 1
f xi , xi 1
f x0 , x1
f x1, x2
.
f xi 1, xi
f xi , xi 1
f xi , xi 1 ,..., xi n
f xi , xi 1 , xi 2
f xn 2 , xn 1
f xn 1 , xn
f xn , xn 1
f xi , xi 1 ,..., xi n 1
f x0 , x1, x2
.
…
f xi 1 , xi , xi 1
f x0 , x1 ,..., xn 1 , xn
…
.
или xn 1 xn
.
f xn 2 , xn 1 , xn
f xn 1 , xn , xn 1
f x1 , x1 ,..., xn 2 , xn 1
f x0 , x1 ,..., xn , xn 1

9. Интерполяционный полином Ньютона. Пример.

f x sin x ,
2
x 0,1
i 0,1
xi
0
1
f xi
0
1
xi
0
fi
0
f xi , xi 1
f x0 , x1
1
0 1
1
0 1
1
N1 x f x0 x x0 f x0 , x1 0 ( x 0) x,
N1 x L1 x

10. Интерполяционный полином Ньютона. Пример.

xi
fi
0
0
f xi , xi 1
f x0 , x1
1
f xi , xi 1 , xi 2
0 1
1
0 1
1
f x0 , x1 , x2
f x0 , x1 f x1 , x2 1 2 2
2 2 2
1
x0 x2
0
2
2
2 2 2
f x1 , x2
1
1
2
1
1
2
2
2
N2 x f x0 x x0 f x0 , x1 x x0 x x1 f x0 , x1, x2 ,
N 2 x N1 x x x0 x x1 f x0 , x1 , x2 ,
N 2 x x x 0 x 1 2 2 2 x 1 2 2 2 x 2 2 2 x 2 2 1 2 2 2 x 2 ,
N2 x L2 x

11. Интерполяционный полином Ньютона. Пример.

i 0,1,2
xi
0
1
1
2
L2 x f 0
f xi
0
1
2
2
x x1 x x2 f x x0 x x2 f x x0 x x1
x0 x1 x0 x2 1 x1 x0 x1 x2 2 x2 x0 x2 x1
L2 x 0
x 1 x 1
x 0 x 1
2 x 0 x 1
2
2
1
1
2 1
1
1
0 1 0 1 0 1
0 1
2
2
2
2
2x2 x 2 2 x2 2 2 x 2 2 2 x2 2 2 1 x

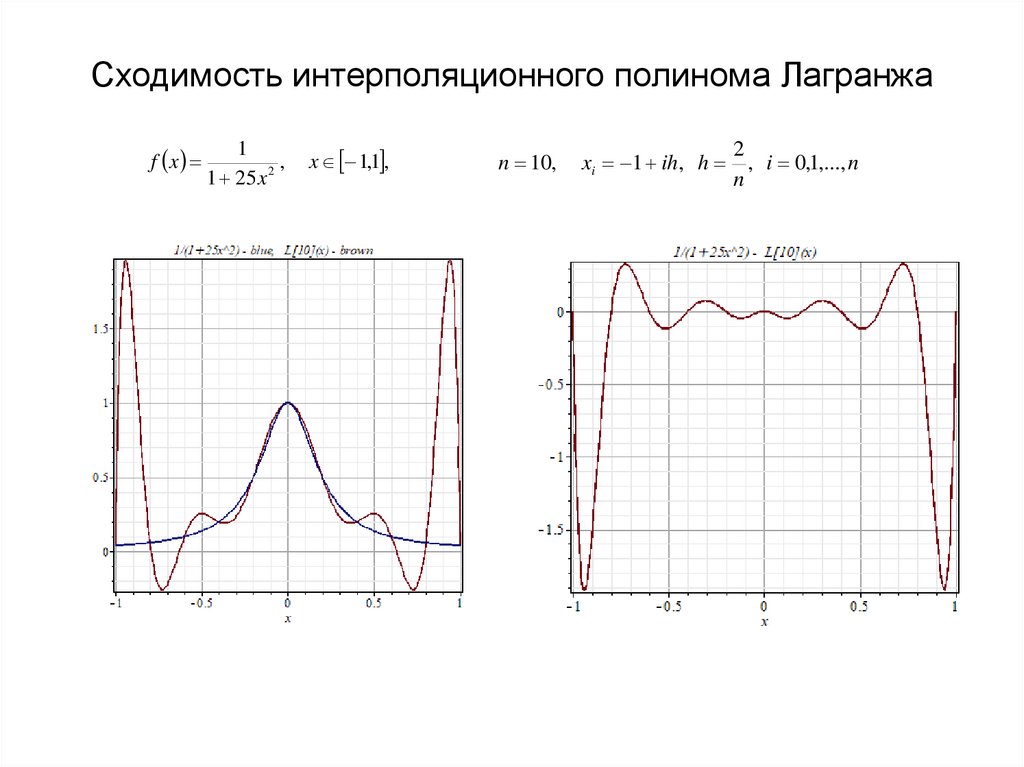
12. Сходимость интерполяционного полинома Лагранжа

f x
1
,
1 25 x 2
x 1,1 ,
n 10,
xi 1 ih , h
2
, i 0,1,..., n
n

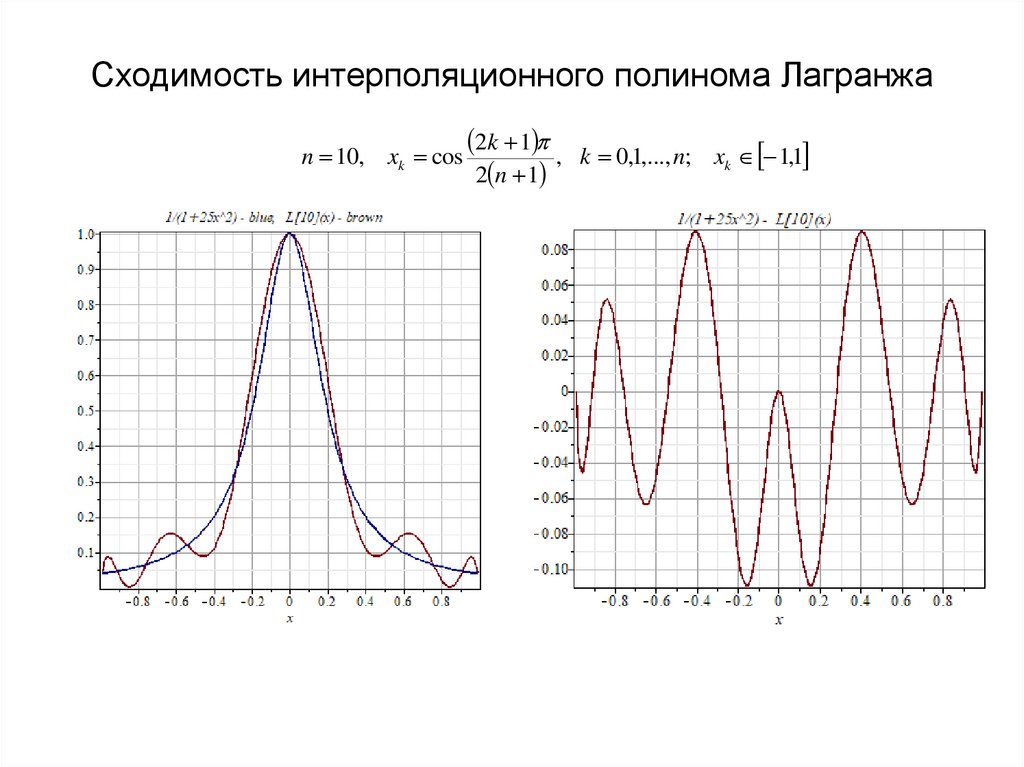
13. Сходимость интерполяционного полинома Лагранжа

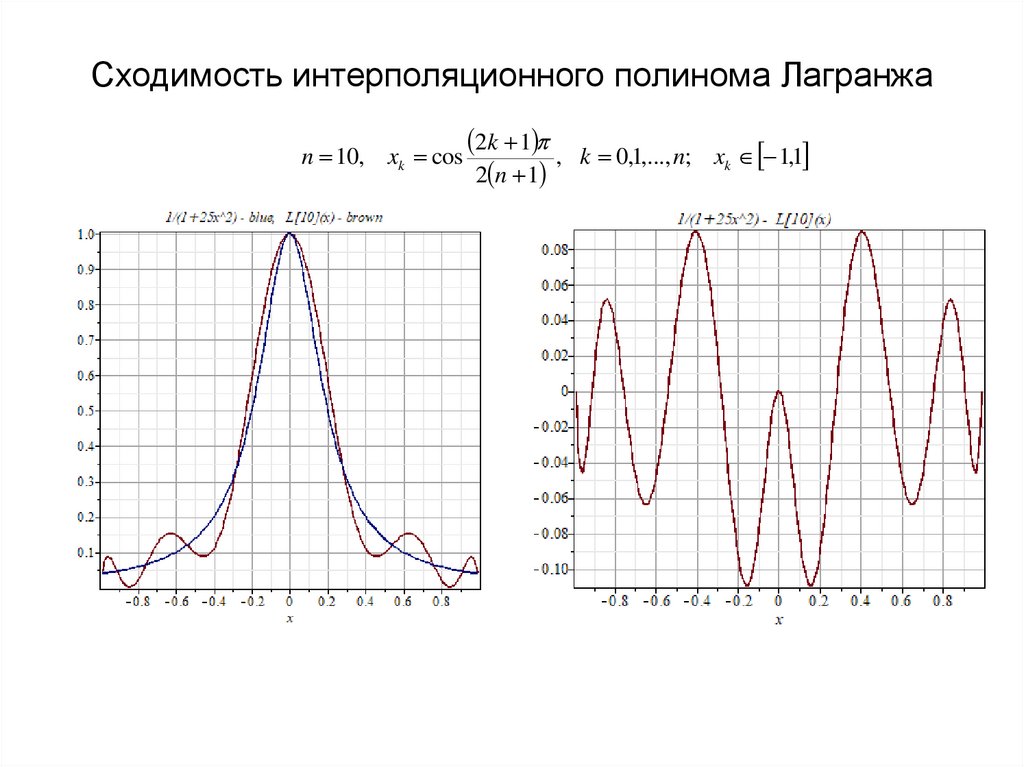
n 10, xk cos
2k 1 , k 0,1,..., n;
2 n 1
xk 1,1

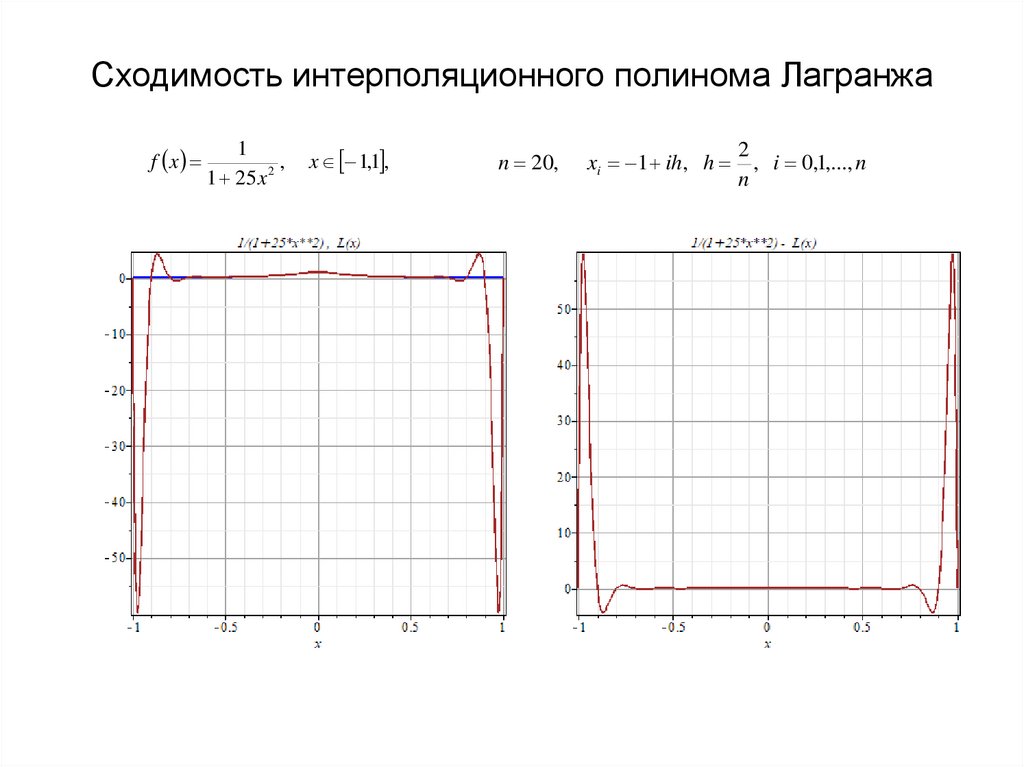
14. Сходимость интерполяционного полинома Лагранжа

f x
1
,
1 25 x 2
x 1,1 ,
n 20,
xi 1 ih, h
2
, i 0,1,..., n
n

15. Сходимость интерполяционного полинома Лагранжа

n 10, xk cos
2k 1 , k 0,1,..., n;
2 n 1
xk 1,1

16. Сходимость интерполяционного полинома Лагранжа

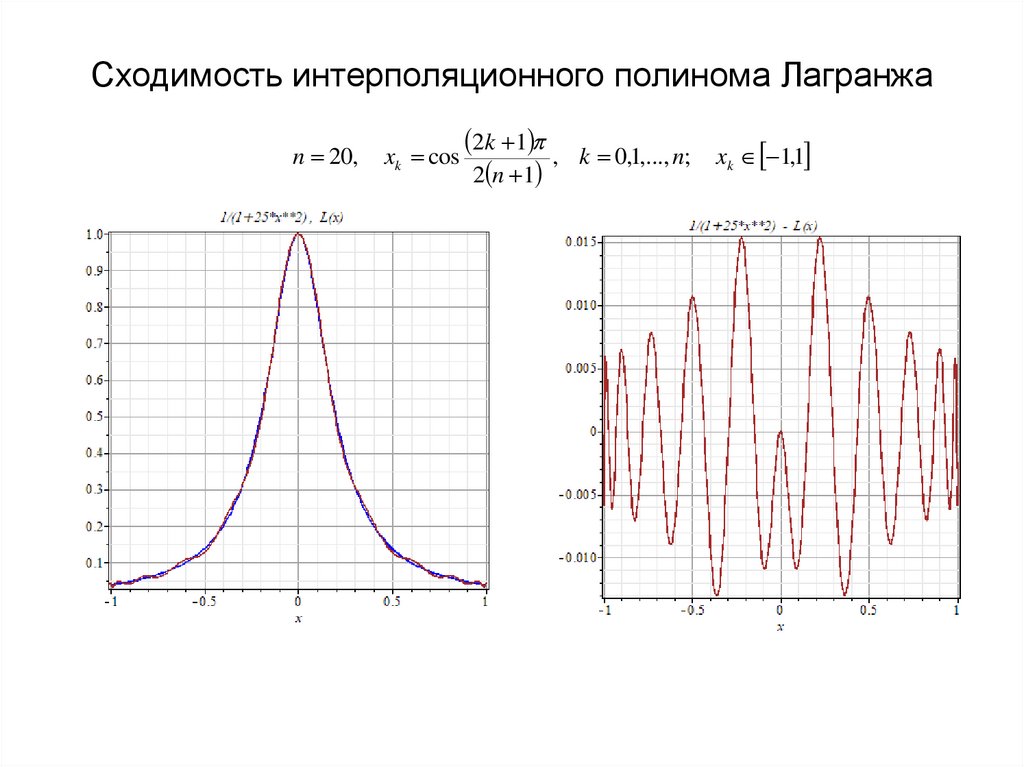
n 20,
xk cos
2k 1 , k 0,1,..., n;
2 n 1
xk 1,1